Floquet spectrum and universal dynamics of a periodically driven two-atom system
Wenzhu Xie(謝文柱), Zhengqiang Zhou(周正強(qiáng)), Xuan Li(李軒),Simiao Cui(崔思淼), and Mingyuan Sun(孫明遠(yuǎn))
School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China
Keywords: Floquet spectrum,universal dynamics,two-atom system,avoided crossing
1.Introduction
Nonequilibrium physics attracts more and more attention from researchers in various areas such as atomic physics,condensed matter physics, and cosmology.Although it has obtained significant progress recently, many fundamental problems are still not solved, due to the complex interaction involved generally.[1–3]With advance of experimental techniques,ultracold atoms can now be highly controllable,which makes them an excellent platform for research of nonequilibrium phenomena.[4,5]Because ultracold atomic gases are quite dilute, the typical many-body timescales can be much larger than that of a typical operation.Quench dynamics becomes one of the most studied nonequilibrium dynamics,where universal features are observed.[6–13]
Periodic driving is another important method to study nonequilibrium physics, which can also lead to novel phenomena such as dynamical localization,[4]discrete time crystal,[14–21]and many-body echo.[22–24]In ultracold atomic gases, it can be realized by modulating the harmonic trap or the interaction strength.The latter can be tuned via a Feshbach resonance in experiments.[25]The periodically driven system can be described in the framework of Floquet theory,where the properties of the system are effectively determined by the time-independent Floquet Hamiltonian.[4,26]Previous works demonstrate that periodic driving can trigger various excitations in few-body systems,[27–31]as well as in many-body systems.[32–44]However, properties of the quasienergy spectrum and its relation to the dynamics behavior have not been thoroughly discussed yet.Therefore,an important problem is what the possible universal relation between the dynamics and the Floquet spectrum is,which needs further investigation.
Few-body systems play an important role in research of both equilibrium and nonequilibrium physics.On the one hand,they can exhibit some interesting features on their own,for example,Efimov effect[45]and dynamic fractal.[46]On the other hand,they can often provide some insights for analyzing more complicated many-body systems.[47–52]Although they have been extensively studied in stationary conditions, their time-dependent counterpart is still not understood well.Since the interatomic interaction can play an essential role in the time evolution of few-body systems, it is imperative to study how the periodically driven interaction affects the dynamics.
In this work, we take a two-atom system in a threedimensional harmonic trap as a typical example to investigate the effect of periodically driven interaction.The Floquet spectrum and dynamics of a periodically driven two-atom system in three dimensions is demonstrated quantitatively,which can not be derived by previous works.Two different kinds of modulations are used to search for some universal features.Indeed,we find similar characteristics of the Floquet spectrum and the dynamics in both the cosine and the square-wave modulations.As the driving frequency increases,the quasienergy levels repeat accumulating and spreading.At the accumulation point,the system is excited to higher and higher energy state,while it is bounded otherwise.Although the specific features can vary in different parameter regions,the corresponding relation between the Floquet spectrum and the dynamics is universal.Moreover, we propose a mechanism for selectively exciting the system to a specific state by using the avoided crossing of two quasienergy levels.
This article is organized as follows.In Section 2, we introduce our model and method in detail.In Section 3, we investigate the cosine modulation, and calculate the Floquet spectrum and the dynamics of the energy as well as the population of different instantaneous eigenstates.Two kinds of main features are found in both the spectrum and the dynamics.Moreover, the relation between them are analyzed carefully.We study in Section 4 the square-wave modulation and focus on the comparison with the results of the cosine modulation.Finally,we give a brief summary in Section 5.
2.Theoretical model
We study a two-body system with a periodical contact interaction in a three-dimensional isotropic harmonic trap.Specifically, we consider two atoms with equal massmand their positions are denoted byr1andr2, respectively.The contact interaction between them is described by the Fermi pseudopential.[53]Therefore, the dimensionless Hamiltonian can be written as
Here,Γ(x)represents the gamma function.The numerical results for various scattering lengths are shown in Fig.1(a).
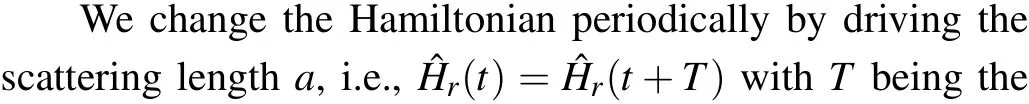

whereεn ∈[-πω,πω] is the quasienergy,nis a positive integer;ω=2π/Tdenotes the driving frequency.In fact, the Floquet states|ψn(t)〉 constitute a complete orthonormal basis at any fixed timet.Hence one can express the initial state as|Ψ(t0)〉=∑n Dn(t0)|ψn(t0)〉, where the coefficients can be written asDn(t0)=〈ψn(t0)|Ψ(t0)〉.By applying the time evolution operator ?U(t0+T,t0)on both sides formtimes and using Eq.(4),one can readily obtain the stroboscopic time evolution of|Ψ(t0+mT)〉as

Fig.1.(a) Eigenenergies for various scattering length a,[53] obtained from Eq.(3).For any scattering length a,there are a series of eigenenergies Ei.When a →±∞,Ei =0.5,2.5,4.5,...and when a →0+,one binding energy tends to negative infinity and the other energies are 1.5,3.5,5.5,...(b) The energy differences between neighboring levels Ei+1-Ei as a function of a for i = 1,2,3,4 (from bottom to top at a<0).As a →∞or a →0,the energy difference tends to be 2,except the one between the ground state and the first excited state for a →0+.
The Floquet states att0and quasienergies can be obtained by calculating the eigenvalues and eigenstates of the timeevolution operator over one period, i.e., Eq.(4).It can be calculated numerically in the following way.One period can be divided intoNsmall time intervals ?twith ?t=T/N,and for thej-th (j=1,...,N) interval, the time-evolution operator can be written as ?Uj(t0)=U(t0+j·?t,t0+(j-1)?t)≈exp[-i?t?H(t0+(j-1)?t)].Therefore,over the whole cycle,the time evolution operator can be expressed as


3.Cosine modulation
We first study the cosine modulation.Initially, the two particles are taken to be at the ground state with a scattering lengtha(t=0).Then we change the scattering lengthain the form ofa(t)=a0+?a·cos(ωt) with a periodT, whereω=2π/Tand ?aare the frequency and amplitude of the modulation, respectively.We first study the case with the initial scattering lengtha(t=0)=0 and a small amplitude, where for any instantaneousa(t),the energy spectra can be approximately viewed as equally spaced(see Fig.1(b)).
From Eq.(6),one can calculate the time evolution operator for one driving period ?U(t0+T,t0).Then through Eq.(4),one can obtain the quasienergiesεnand the corresponding Floquet states|ψn(t0)〉.The dependence of the quasienergies on the driving frequencyωis shown in Fig.2.A typical feature of the spectrum is the accumulation of quasienergy levels at the even driving frequencies (ω=2,4,6,...), while in other positions they are spread out across the region.

Fig.2.Floquet spectrum of the cosine modulation as a function of the driving frequency ω with a0=-0.05 and ?a=0.05.
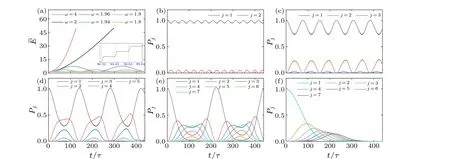
Fig.3.Time evolution of the energy and the population of the instantaneous eigenstate for the cosine modulation with a0 =-0.05 and ?a=0.05.(a)Time evolution of the energy for various driving frequencies,exhibiting two kinds of dynamical behaviors,(b)–(f)time evolution of the occupation probability for ω =1.8,ω =1.9,ω =1.94,ω =1.96,and ω =2.
One fundamental problem is what kinds of dynamics are associated with these two different spectral features.In other words,what is the relation between the dynamic behavior and the quasienergy spectrum in the Floquet system? To answer this question,we calculate the dynamics of the system and the results are displayed in Fig.3.Similarly to the spectrum, the dynamics of the energy can also be divided into two categories,i.e., collective excitations (i.e., the system is successively excited to higher states)and the stable oscillating.As shown in Fig.3(a), the expectation value of the energy increases at the driving frequencyω=2,4,..., where quasienergy levels are accumulating and forming close to continuous areas.Moreover, the expectation value increases faster and faster as the even driving frequency increases.However,asωmoves away from the resonant frequency, the energy becomes oscillating steadily.It is worth mentioning that,at the resonant frequency,t he expectation value of the energy rises in a stepwise manner with a period of about 2π/ω,as shown in the inset of Fig.3(a).
In order to interpret the physical processes involved in the above dynamics, we investigate the population of different instantaneous eigenstates in detail.When the driving frequency is away from the resonant position, the population of the ground state dominates while the frist excited eigenstate acquires the rest approximately, as shown in Fig.3(b).As the driving frequency gradually approaches to the resonance,higher excited eigenstates gain more population.However, it is important to emphasize that there are no transitions that go from the ground state to an excited state completely,as shown in Figs.3(c)–3(e).Therefore,it is very different from the Rabi oscillation,which is associated with only two states.The population of the instantaneous ground state exhibit a regular oscillation and the minimal value can be reduced to 0 in some region, as shown in Fig.3(e).The instantaneous eigenstates from the second-excited one to the sixth-excited one can gain population,while the population of the ground state decreases.However, at resonance, as the population of the ground state decreases to 0 gradually, the population of excited states first increases and then decreases to 0 [see Fig.3(f)].As time increases, higher and higher states are involved in this similar varying manner,which indicates that the system gains energy constantly and is excited to higher and higher states.Note that the population is only shown for the first several eigenstates in Fig.3(f)and the population for the rest exhibits the same trend with delayed appearance.Therefore,the occupation probability is conserved as it should be.
The above results demonstrate that the dynamics of the Floquet system is closely related to the properties of the quasienergy spectrum.[28–30,33]The aggregation and dispersion of the quasienergies correspond to different dynamical behaviors.The energy is constantly gained at the resonant frequency where the quasienergies accumulate.However, when the quasienergies are dispersed, the time evolution of the energy exhibits oscillating behavior.
We find that when the initial scattering length isa(t=0)=0 and the driving amplitude is small,the population does not completely transfer between the two states.A natural question is whether a complete transfer can occur in other regimes.To address this problem, we investigate the Floquet spectrum with various parameters in detail.When one changesa0and ?a,some interesting new features appear.Some typical results are displayed in Fig.4.In order to conveniently compare different results and to analyze the dynamics later,we label the quasienergy in the following way.For the Floquet state|ψn〉, according to its overlap with the different eigenstates?j, the quasienergy level is denoted asεjif the corresponding overlap|Dn j| is the largest.In this way, theε1(red line)andε2(blue line)can be labelled in Figs.4(a)–4(d).Their locations relative to other quasienergy levels can be significantly modified as the driving parameters vary.For example, whena(t=0)=1 ora(t=0)=-1, these two quasienergy levels are clearly separated from others[see Figs.4(a)–4(d)].
In fact,the first and second quasienergy levels are closely related to the first and second eigenenergy levels for the scattering lengtha(t= 0).If the difference between the first and second eigenenergy levels is much larger than the differences between other neighboring eigenenergy levels, the first quasienergy level will be far away from the accumulation point.For example, as shown in Fig.4(a), fora(t=0)=1,the difference between the first and second eigenenergy level isE2-E1=3.02, while the difference between the second and the third one isE3-E2=2.09, as the energy level increases,the difference between neighboring energy levels becomes smaller and approaches to 2.In this case,the distance between the first quasienergy level and the accumulation point is approximately 3 forω= 2.When|a(t= 0)| increases,the difference between the first and second eigenenergy levels gradually becomes 2.Therefore,in the quasienergy spectrum,the first and second quasienergy levels move closer to the accumulation point,as shown in Figs.4(b)–4(d).
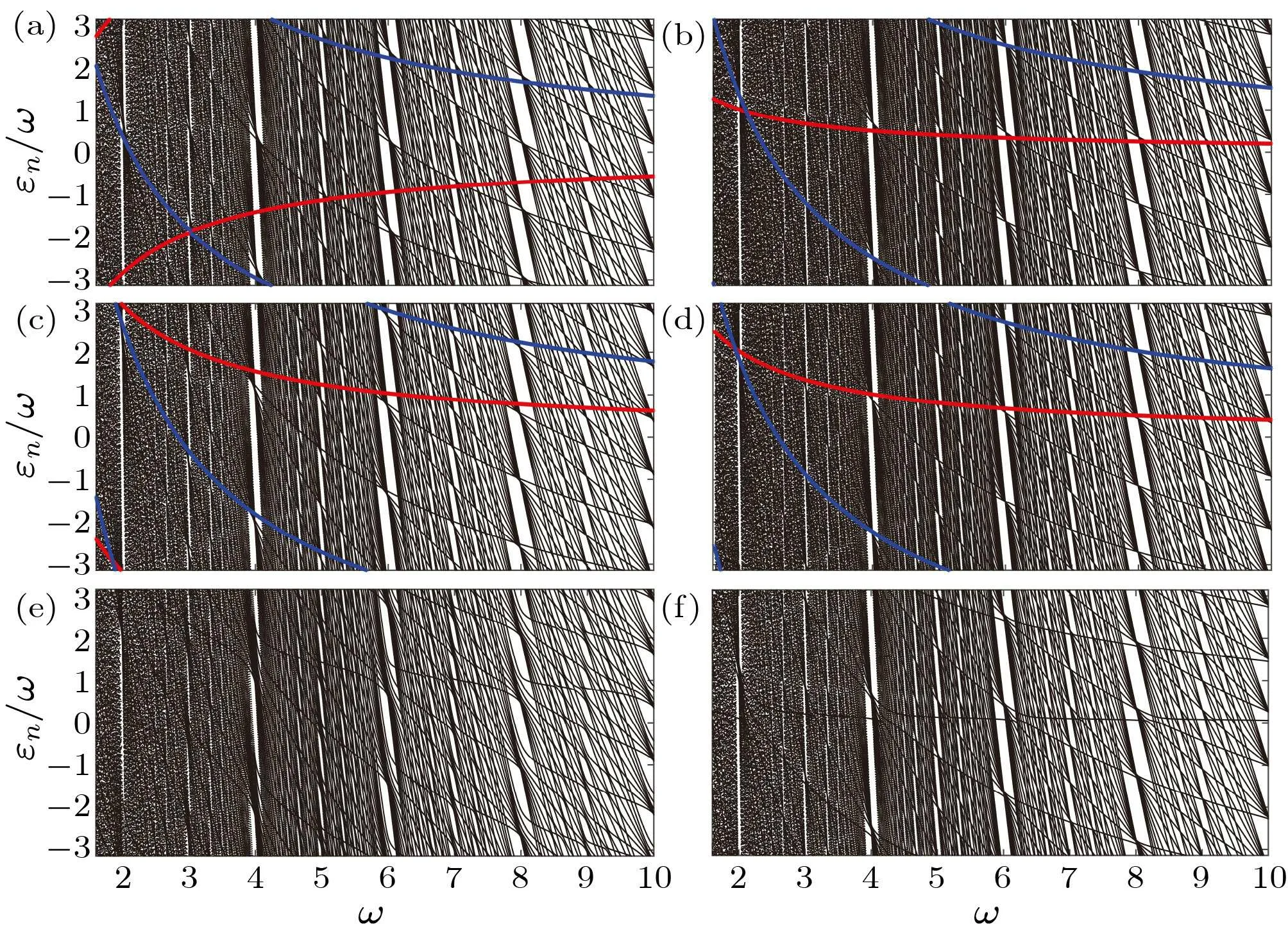
Fig.4.Floquet spectrum of the cosine modulation with different driving parameters: (a)–(d) a0 =1.05, 5.05, -1.05, -5.05 with ?a=-0.05.The red line and blue line denote the ground state and the first excited state,respectively,which indicates the significant influences of the initial scattering length a0 and the driving amplitude ?a on the spectrum.(e)a0=-1 and ?a=1,(f)a0=3.5 and ?a=-2.5.
When the driving amplitude is large,the overlap between different eigenstates and the Floquet mode can be comparable,and no one is dominant.As a result, the method previously used to define quasienergy levels is no longer applicable.Figure 4(e) shows the quasienergy spectrum for a large driving amplitude anda(t=0)=0.The basic characteristics are similar to those with the small amplitude(see Fig.2),except for the less accumulation.This is caused by the significant change of adjacent eigenenergy differences for varying scattering lengths arounda=0.Figure 4(f) displays the quasienergy spectrum for a large driving amplitude anda(t=0)=1.When the driving frequencies are even, most quasienergy levels converge into dense regions.The adjacent eigenenergy differences tend to be the same at larger scattering lengths, and increasing the amplitude can change the relative positions of the quasienergy levels[see Figs.4(a)and 4(f)].
Overall, Fig.4 demonstrates the effect of the initial swave scattering length and the driving amplitude on the Floquet spectrum.One can conclude that the Floquet spectrum can be adjusted by the initial s-wave scattering length and the driving amplitude quantitatively, although they looks similar qualitatively.
Moreover,when the initial scattering lengtha(t=0)?=0,an avoided crossing occurs between two quasienergy levels,where the frequency is not equal to the resonant frequency.In the following,we focus on analyzing the characteristics of avoided crossings in the quasienergy spectrum and the corresponding dynamics of the system.
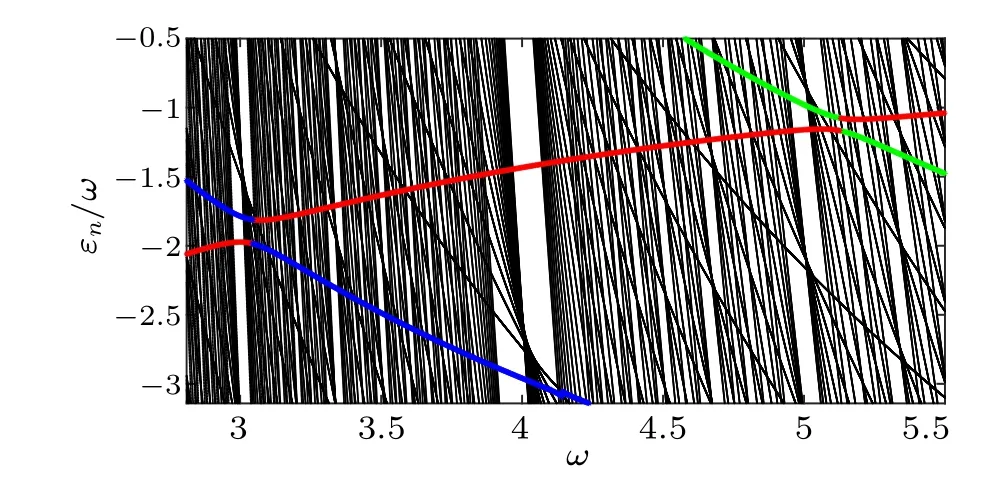
Fig.5.Avoided crossings between two quasienergy levels of the cosine modulation with a0 =0.95 and ?a=0.05.The red, blue, and green represent the first,second,and third quasienergy levels,respectively.
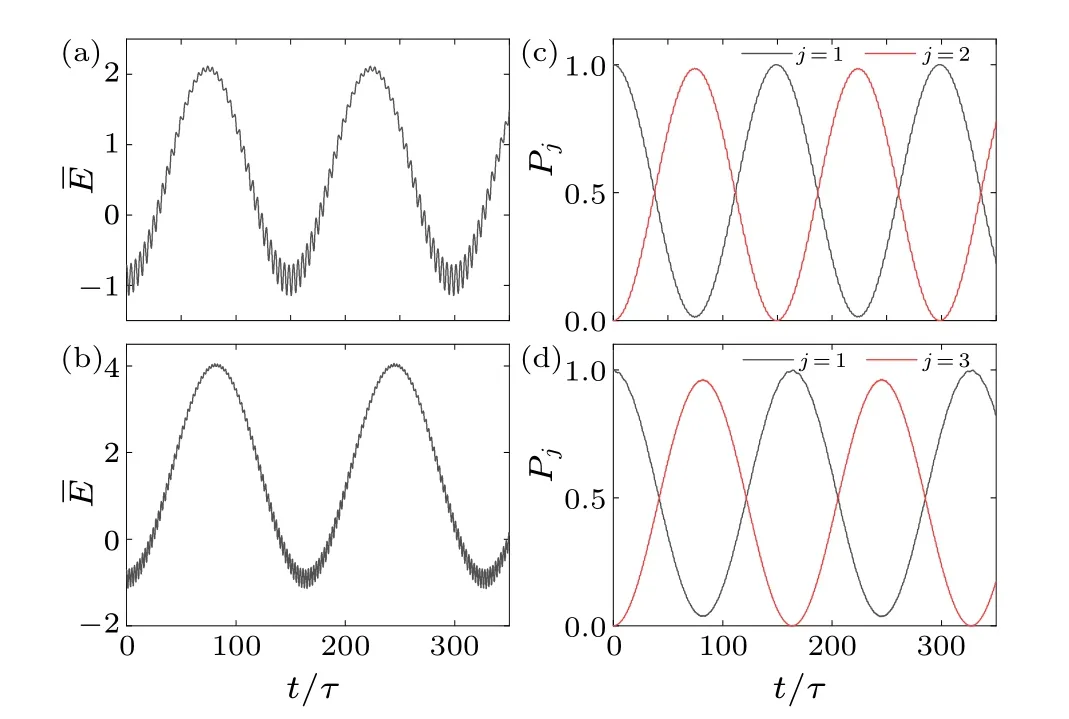
Fig.6.Time evolution of the energy and the population as two quasienergy levels undergo the avoided crossing, for the cosine modulation with a=0.95 and ?a=0.05.[(a), (c)] The evolutions of the expectation value of the energy and the population,respectively,when avoided crossing occurs between the first and the second quasienergy levels with a driving frequency of ω =3.12.[(b), (d)] The evolution when avoided crossing occurs between the first and third quasienergy level with a driving frequency of ω =5.22.
When we take the cosine modulation parameters asa0=0.95 and ?a=0.05,avoided crossings can appear in the Floquet spectrum, as shown in Fig.5.The red, blue, and green lines denote the first three quasienergy levels.One can see that avoided crossings occur at specific frequencies between the first and second quasienergy level, as well as between the first and third quasienergy level.Furthermore, the driving amplitude can significantly modify the frequency for the avoided crossing, especially when the slope of the difference between adjacent instantaneous eigenenergies changes rapidly with the scattering length [Fig.1(b)].The frequencyωfor the avoided crossing between thejth quasienergy level and the first quasienergy level approximately satisfies the following relation:
where(Ej-E1)arepresents the difference between thejth and first eigenenergy for the scattering lengtha.
Around the avoided crossing point, the evolution of the energy ˉEand the population of the instantaneous eigenstatePjoscillate periodically, as shown in Fig.6.Note that the evolution of the populationPjis performed between the eigenstates?jand?1,where?jcorresponds to thejth quasienergy level that has an avoided crossing with the first quasienergy level.Furthermore, the population of the?1can completely be transferred to thejth eigenstate.Therefore,one can set the modulation frequency at the position of the avoided crossing to achieve the periodic oscillation between the ground state and that eigenstate.
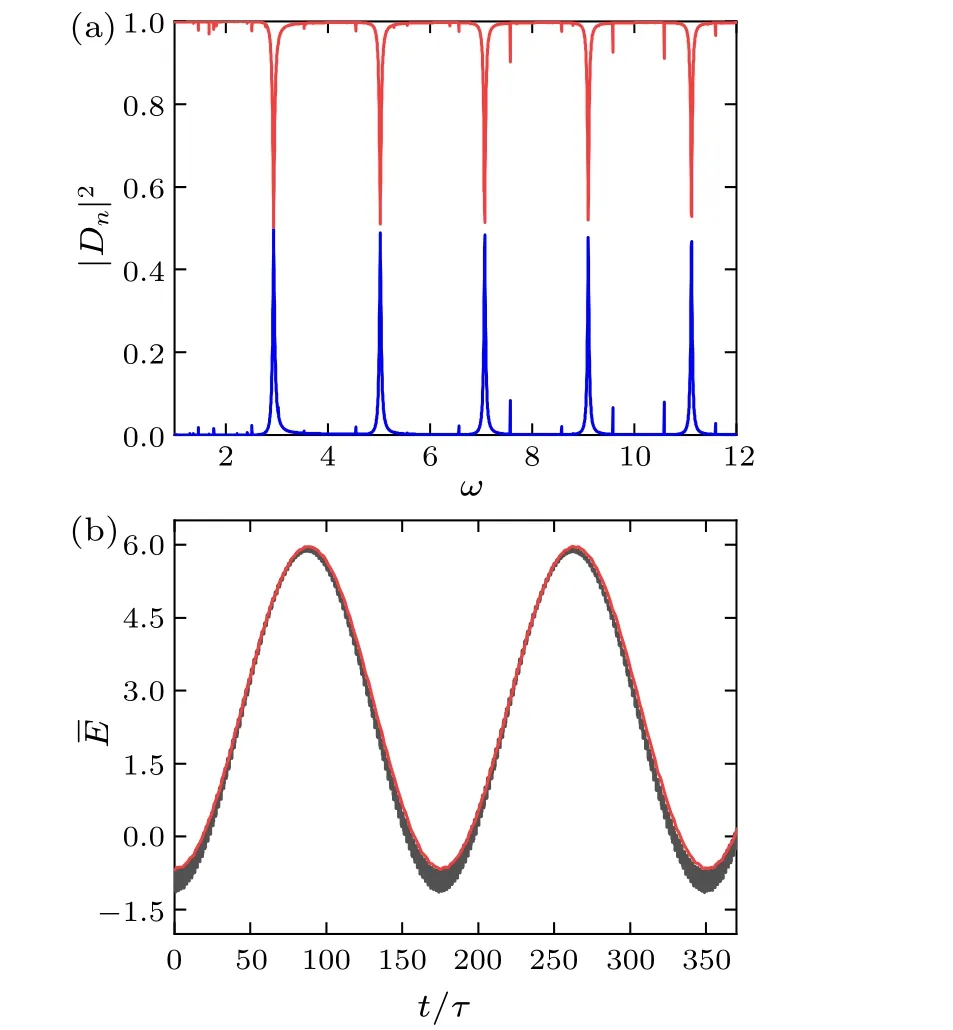
Fig.7.(a)The two largest probabilities|Dn|2 as a function of the driving frequency ω for the cosine modulation with a0 =0.95 and ?a=0.05,where the red line and blue line denote the first and second largest probabilities, respectively.(b)The evolution of the energy obtained by expanding the initial state over the two Floquet states, |ψ1〉 and |ψ4〉 for the cosine modulation with a0 =0.95, ?a=0.05, and ω =7.07.It is represented by the red line,which is compared with the exact result(the black line).
The coefficients of the two most populated Floquet modes,|D1|2and|D2|2are shown as a function of the driving frequency in Fig.7(a).Apparently,|D1|2and|D2|2are only comparable when avoided crossings occur.Otherwise,only a single Floquet mode is notably populated.When|D1|2is close to 1, the stroboscopic time evolution [see Eq.(5)]becomes, to a good approximation, periodic with the period ofT.When|D1|2≈|D2|2, the evolution of the initial states includes an interference term between|ψ1〉 and|ψj〉.The micromotion shows a cyclic oscillation, whose period is determined by the corresponding quasienergies through the relationTosc/τ= 2π/|εj-ε1|.For example, when the driving frequencyωis equal to the one at which the third and the first quasienergy level undergo the avoided crossing,the period isTosc/τ= 2π/(ε3-ε1) = 168.45.The wave function can be approximately expressed asΨ(r,t0+mT)≈D1ψ1e-iε1mT/(2π)+Djψje-iεjmT/(2π).Therefore, one can obtain an approximate result for the time evolution of the energy at timemT[see Fig.7(b)], which agrees well with the exact result.
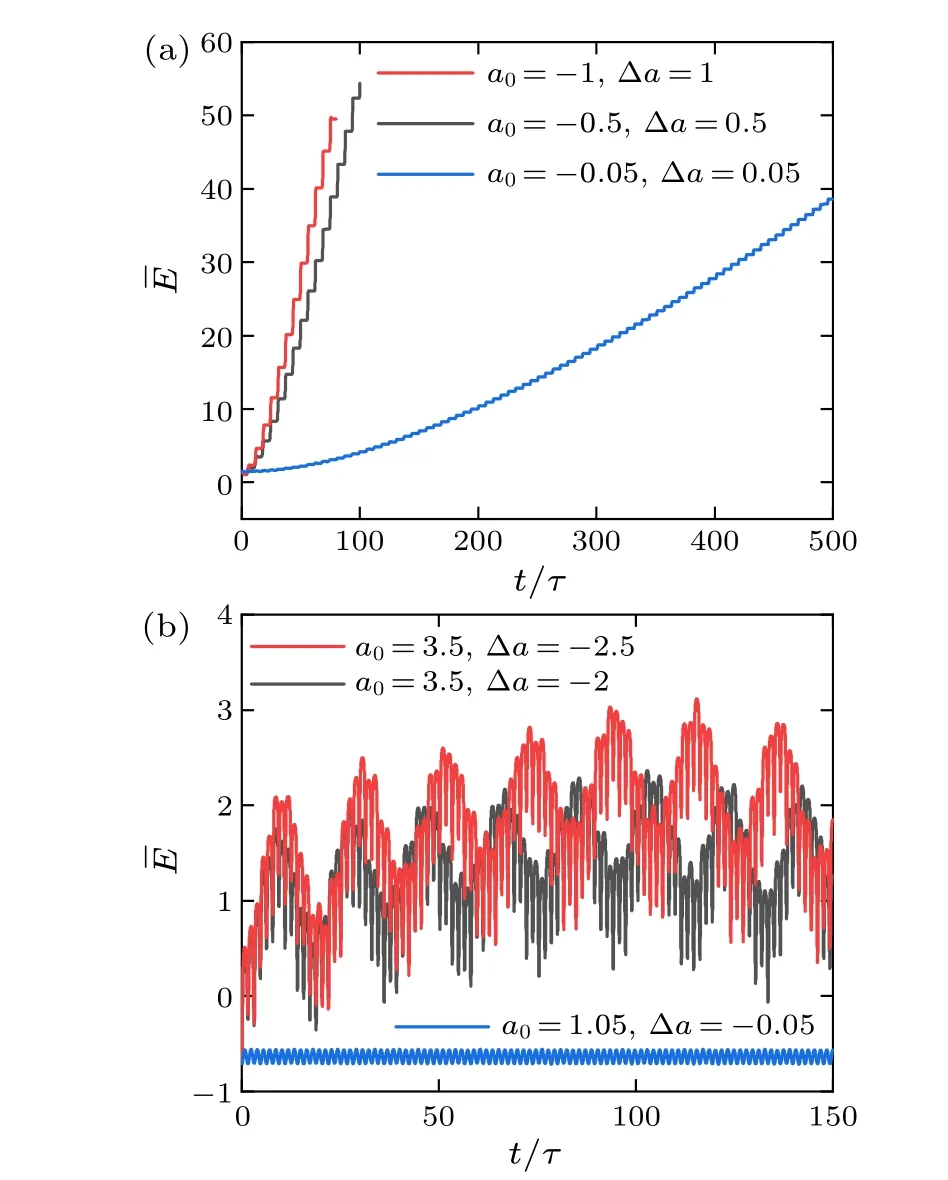
Fig.8.The evolution of the energy for the cosine modulation as the driving amplitude increases.(a) Initial scattering length a(t =0)=0 and driving frequency ω =2.(b)Initial scattering length a(t =0)=1 and the driving frequency ω =4.
For large driving amplitudes, we divide the discussion into two parts based on the initial scattering length.When the initial scattering length is zero, i.e.,a(t=0)=0, from the perspective of the quasienergy spectrum, the quasienergy spectrum becomes sparser as the amplitude increases.However,the initial state is distributed in higher Floquet states,resulting in a faster increase of the energy,as shown in Fig.8(a).When the initial scattering length is fairly large, at small amplitudes and even driving frequencies,the Floquet stateψ1almost contributes entirely to the energy.Thus, the energy oscillates periodically within a small range.As the amplitude increases, from the perspective of the quasienergy spectrum,quasienergy levels at even driving frequencies can gradually converge to some dense region.Therefore,more Floquet states are involved in the dynamics,which make the system excite to high-energy states[see Fig.8(b)].
4.Square-wave modulation
In this section, we study the effects of a square-wave modulation on the Floquet spectrum and dynamics of the system.It can be expressed as
whereT=2π/ωandnis an integer withn ≥0.A square wave can be viewed as a superposition of multiple cosine waves with different frequencies.Therefore, the interplay of them may lead to some new phenomena.

Fig.9.Floquet spectrum of the square-wave modulation with a1 =0 and a2=-1.
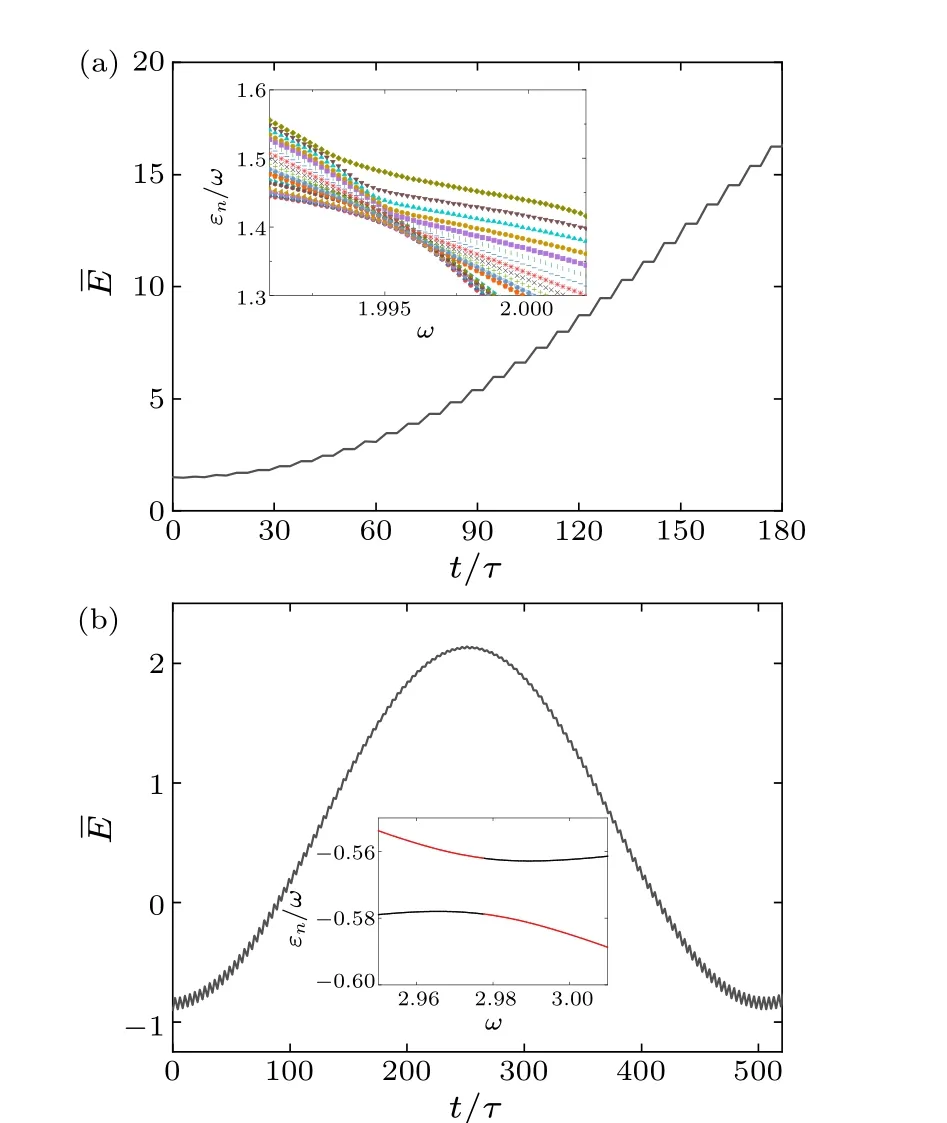
Fig.10.The evolution of the energy for different quasienergy spectrum features (inset) in the square-wave modulation: (a) for the accumulation of quasienergy levels with a1 =0, a2 =-0.05, and ω =1.995,(b) for the avoided crossing of two quasienergy levels with a1 =-1,a2=-1.05,and ω =2.976.
For a small driving amplitude, as we have checked, the square-wave modulation has the similar characteristics of the Floquet spectrum to the cosine modulation(see Fig.2).This is due to the fact that the main contribution is from the first component (with the frequencyω).However, as the driving amplitude increases,the Floquet spectrum becomes quite different,due to the influence of other components with different frequencies.The Floquet spectrum fora1=0 anda2=-1 is displayed in Fig.9.The accumulation region is split into two parts at the resonant frequencies (i.e.,ω=2,4,6,...), which is associated with the difference between the energy levels fora=0 anda=-1(see Fig.1).
However,the correspondence between quasienergy spectrum and dynamical behavior of the system is still valid.When the quasienergy levels converge into a dense region[inset of Fig.10(a)], the system is persistently excited, resulting in a continuous increase of the average energy, as shown in Fig.10(a).When thejth quasienergy level and the first quasienergy level undergo the avoided crossing at a specific driving frequency [inset of Fig.10(b)], the atoms can be excited into the corresponding instantaneous eigenstates and undergo periodic oscillations between these two states, which further leads to periodic oscillations of the energy evolution[see Fig.10(b)].
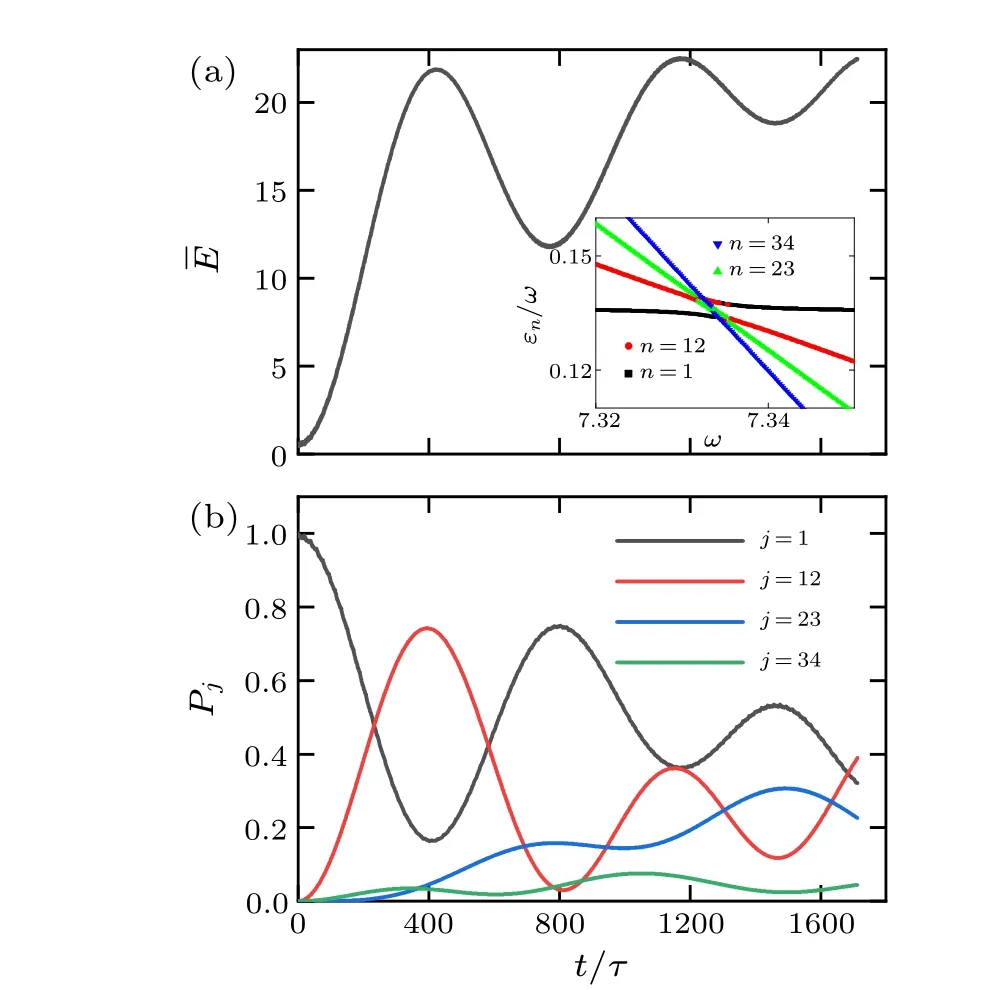
Fig.11.Evolutions of the energy (a) and the population (b) as several energy levels undergo the avoided crossing [inset in (a)] with ω =7.334,a1=-10 and a2=10 in the square-wave modulation.
The difference from the cosine modulation is of the locations where the avoided crossings of the quasienergy levels are not limited to special values.In particular, for some frequencies,there are multiple energy levels that undergo the avoided crossing,where the atoms can be excited to the corresponding high eigenenergy levels, as shown in Fig.11.Therefore, the energy increases and oscillates,due to the varying occupation among these avoided crossing states.
5.Conclusion
In summary, we have investigated the effect of a periodically driven interaction on the Floquet spectrum and the dynamics of a two-atom system in a three-dimensional harmonic trap.The interatomic interaction strength is modulated by using two different ways,the cosine and square-wave modulations.We find some universal features in both the Floquet spectrum and the dynamics for various parameter regions.Furthermore, their corresponding relation is also universal.Specifically,the quasienergy spectrum exhibits two main distinct features, the accumulating and the spreading.When the involved quasienergies accumulate to one point, the system can be persistently excited to higher and higher energy state.Otherwise,as they deviate from each other,the evolution of the energy is bounded.Moreover, as a typical example, we analyze the avoided crossing of two quasienergy levels carefully,where the system evolves between the two corresponding instantaneous eigenstates with a possible complete transfer from one to the other.This may pave the way for obtaining certain states by utilizing the avoided crossing of their quasienergy levels.Our results can be generalized to three-body systems or other few-body systems in the future.
Through Feshbach resonance,two-body losses can occur in ultracold atom systems, which lead to a complex scattering length.[22,55]We did not include this factor for simplicity in this paper.However, the loss makes the Hamiltonian non-Hermitian and can give rise to novel phenomena,[56–61]such as the complex energy spectrum and the non-equilibrium steady state.In other words,the Floquet spectrum and dynamics can be significantly modified.For example, the collective excitation can be suppressed under certain conditions.These interesting problems need further investigation in the future.
Acknowledgements
We thank Zheyu Shi,Ping Fang,and Yueheng Lan for inspiring discussion.The project was supported by the National Natural Science Foundation of China (Grant No.12004049),and the Fund of State Key Laboratory of IPOC(BUPT)(Grant Nos.600119525 and 505019124).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

