Preparing highly entangled states of nanodiamond rotation and NV center spin

Wen-Liang Li(李文亮) and Duan-Lu Zhou(周端陸),?

1Institute of Physics,Beijing National Laboratory for Condensed Matter Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: nanodiamond,NV center,entanglement

1.Introduction

Experimental accomplishments of cooling and controlling of micro-nano scale particles make it possible to exploit macroscopic quantum systems.The nitrogen-vacancy(NV) centers in diamond have shown impressive applications in quantum sensing, quantum information processing and communications.[1–3]Nanodiamonds with NV centers trapped in vacuum can be cooled into their center-of-mass ground state[4–6]and be used to generate spatial quantum superpositions.[7–10]While in recent years the rotation control of nanoparticle with ultra-high precision[11–15]opens the path to observing and testing rotational superpositions.[16–21]In view of quantum information, the coupling of NV center spin and the nanodiamond rotation contains entanglement resource.[22]Study of the entanglement property of the spin–rotation coupled system may have potential use in quantum sensing and quantum network.

In this paper, we simplify the system to an ideal model by considering the nanodiamond only in an external magnetic field.The nanodiamond is treated as a rigid body and its rotation can be described by angular momentum theory in quantum physics.[23–25]We show that by boosting the external magnetic field strength,a highly entangled state of NV center spin and total angular momentum can be realized asymptotically.tization axis is aligned with the nanodiamond symmetric axis.The ground state structure of the spin-1 NV-center is shown in Fig.1.We suppose the nanodiamond’s mechanic rotation is free.In a magnetic fieldB=Be3along thee3-direction of the space-fixed frame with axes{e1,e2,e3},the spin of the NV-center and the rotation of the diamond are coupled,and the system is described by the Hamiltonian

2.Our model and problem

As shown in Fig.2,we consider a nanodiamond,modeled as a symmetric top whose shape is a tetrahedron.The nanodiamond hosts a single negatively charged nitrogen-vacancy center(NV-)with the spin angular momentum ?Swhose quan-

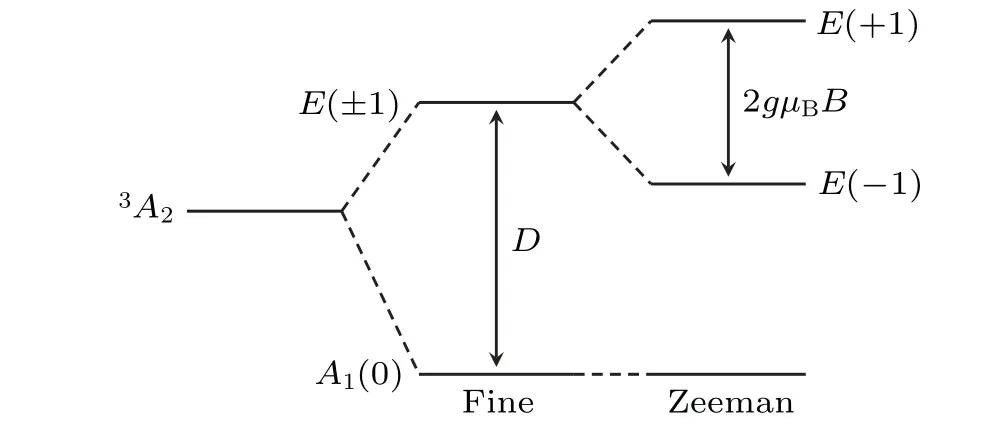
Fig.1.The fine and Zeeman structures of the NV- center ground state.The structure levels are denoted by their spin–orbit symmetry and spin projections m ∈{0,±1}.

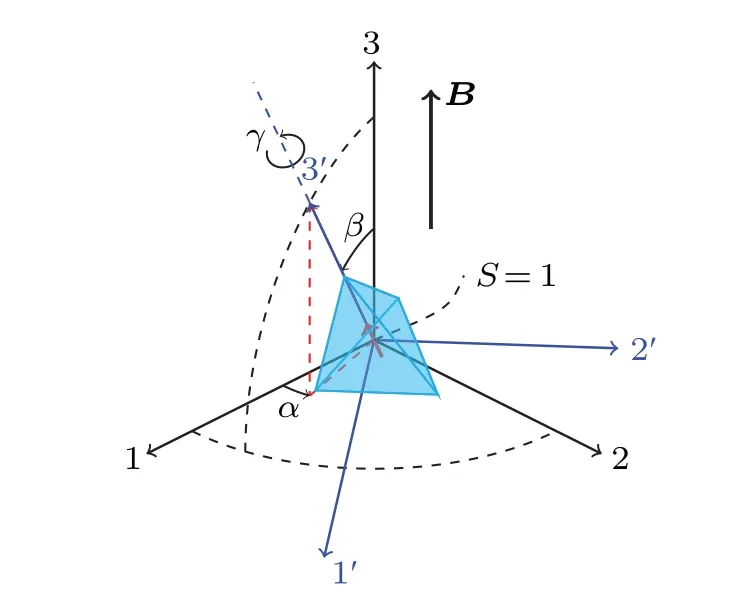
Fig.2.Sketch of the nanodiamond with an embedded NV- center in external magnetic field B.{α,β,γ}are Euler angles between the spacefixed frame and the body-fixed frame.

3.Eigen problem of the Hamiltonian

Before exploring the entanglement between the total angular momentum and the spin in the thermal equilibrium stateρ(B,T)or in the ground state|G(B)〉,it is necessary for us to solve the eigen problem of the Hamiltonian (1).Rewrite the Hamiltonian by inserting ?L= ?J- ?S= ?J+ ?K,

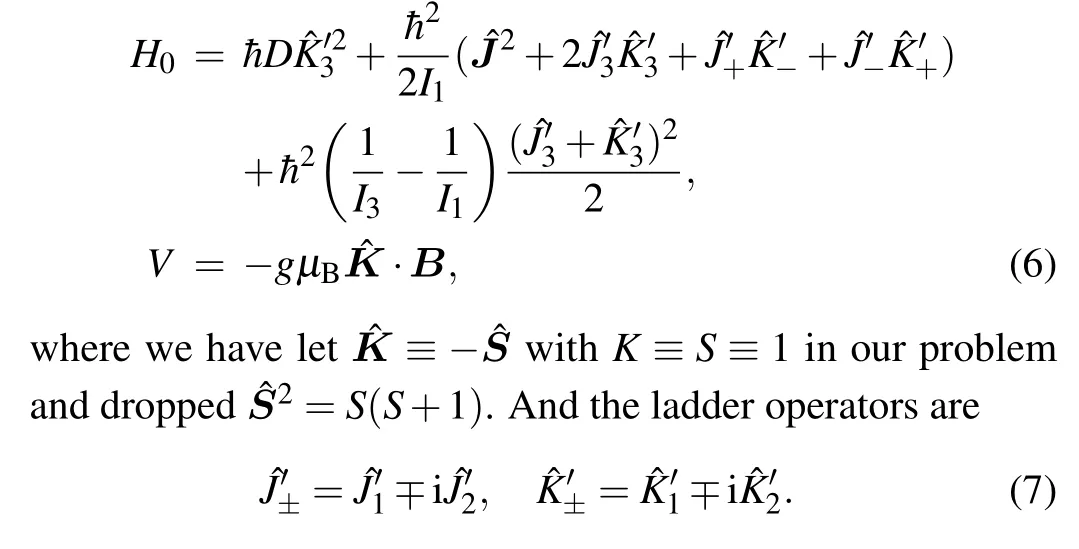
3.1.Basis states based on H0

First we study the degree of the nanodiamond rotation.Because ?Lis an angular momentum operator,it obeys the following commutation relations:

ForK=1,it is convenient to write out the ?K′imatrices

3.2.Analytical matrix elements in V

3.3.Numerical results on eigen energies

Before numerical solving the eigen problem of HamiltonianH, we first need to give the values of the inertia momentum{I1,I2,I3},which are determined by the nanodiamond size.Extremely small(2–5 nm)nanodiamond with an embedded NV center has been reported in recent experiment.[28]In our calculations, we take the bottom side length of the nanodiamonda=1 nm and heighth=1.225 nm,which leads toI1=5.06×10-44kg·m2andI3=3.11×10-44kg·m2.

Since we focus on low energy physics of our system,it is natural to introduce a cutoff via a maximum angular momentumJmaxin our numerical calculations.To ensure the convergence of our physical results, we setJmax=4 (convergence tests see Appendix B).Then we solve the eigen equation of full Hamiltonian

where

The energy levels are shown in Fig.3(b).As a comparison,Fig.3(a)shows the energy levels of the effective spin Hamiltonian

which generally describes a resting NV-center with magnetic fieldB=Be3in NV-axis.While, in our rotating nanodiamond model the direction of NV-axis is given by the quantum state of angular momentum and not along the direction of the fixed magnetic field.

Fig.3.(a)The energy levels of the spin Hamiltonian changing with the external magnetic field B.The crossing of the lowest two energy levels is at B0 ≈0.1 T.(b) The energy levels of the full spin-rotation Hamiltonian in Eq.(1)with Jmax=4.The crossing is at B0 ≈0.036 T.(c)The main probability distribution of the ground state on base kets|JmJkJkK〉with Jmax=4.The insets of(b)and(c)show more details by zooming in.

From Figs.3(a) and 3(b), we observe that in the same magnetic field, the energies of the ground state for our system are similar to those of the Hamiltonian without considering the rotation given by Eq.(41).However, our ground states become highly entangled states which mainly involve six components as shown in Fig.3(c).We can see thatkK=±1 giveskJ=?1 andkK=0 giveskJ=0.As the magnetic field strength increases, the entanglement increases and the probability ofkK=±1 increases while the probability ofkK=0 decreases.The spin component state of the ground state can be used to reflect the total angular moment state and the entanglement between them.

4.Entanglement of thermal equilibrium state

When our quantum system interacts with its thermal environment, it will finally arrive at a steady state: the thermal equilibrium state.Now we are ready to study the entanglement properties in these thermal equilibrium states,which will be useful to guide us to provide a natural protocol to prepare entanglement between nanodiamond rotation and NV-center spin.

4.1.Entanglement of ground states

First we study the entanglement properties of the ground state,i.e.,the thermal equilibrium state when the temperature approaches to zero.For a ground state|G(B)〉JSin magnetic fieldB,the entanglement entropy is defined as

whereρS(B) is the reduced spin density matrix of|G(B)〉JS.Because the dimension of the Hilbert space of NV-center spindS=3, the entanglement entropyS(ρS)≤log23, where the equality is taken if and only if the ground state|G(B)〉JSis maximally entangled.

Numerical results on the entanglement entropyS(ρ(B))are shown in Fig.4(a).With the increase of magnetic fieldB, the entanglement of the ground state grows from 0 to approximately log23, which implies that the ground state approaches to a highly entangled state in a large magnetic fieldB.It seems that there is a curve peak ofΨ1atB0≈0.036 T in Fig.4(a).This is due to the crossing of the lowest two energy levels(see the inset in Fig.3(b)),which also causes the similar phenomena shown in Fig.5.And we notice that the excited state has non-vanishing entanglement atB=0 in Fig.4(a),which causes the non-vanishing negativity forB=0 only at finite temperatures because the thermal equilibrium state is a mixture of all eigenstates.As for why there is entanglement atB=0, it comes from the coupled terms like ?J′i?K′iin Eq.(6) which usually represent the Barnett and Einstein–de Haas effect.[29–31]

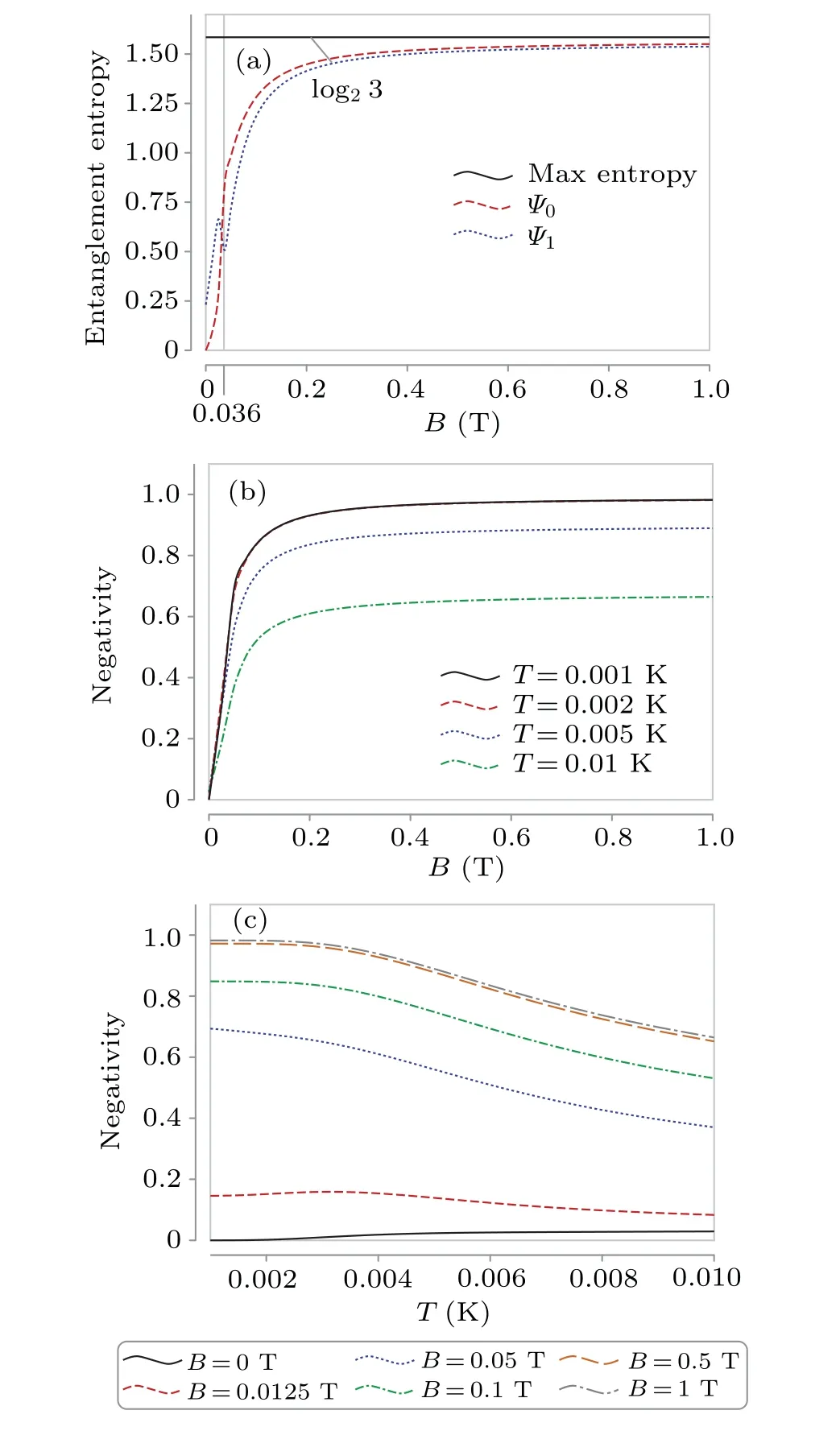
Fig.4.The size of the particle a=1 nm.(a)The entanglement entropy of the ground state and the first excited state compared with the maximum entanglement entropy for the maximum angular quantum number Jmax =4.The negativity of the thermal entanglement state changing(b) with magnetic field B at some fixed temperatures T and (c) with absolute temperature at some fixed magnetic fields B.

4.2.Entanglement of thermal equilibrium states at low temperatures

At temperatureT, the thermal equilibrium state can be represented as

where the partition functionZ= ∑ie-βEi, and|Ψi〉 is the eigenvector ofHwith eigenvalueEi,which has been obtained numerically in the previous section.

Because the thermal equilibrium stateρJS(B,T) is a mixed state, its entanglement can not be characterized by the entanglement entropyS(ρS), which is valid for characterization of entanglement for pure states.To study the entanglement property of the thermal equilibrium state, we introduce another entanglement measure,negativity,[32,33]

The numerical results of the negativity are shown in Fig.4(b).It is observed in Fig.4 that for a given temperatureT,the negativity increases asymptotically to a maximum value with increasing magnetic fieldB.The lower the temperature, the larger the maximal value of the negativity.As shown in Fig.4(c),for a fixed magnetic fieldB,the negativity decreases with increasing absolute temperatureT.The larger the magnetic field, the larger the negativity.Our numerical results show that to obtain a thermal equilibrium state highly entangled,we need to increase the magnetic field above 0.5 T and decrease the temperature below 2 mK.

Based on the above numerical results,we propose a simple protocol to asymptotically prepare a highly entangled state between mechanical rotation of the nanodiamond and the electron spin of NV-center.First, cool down the system to below 2 mK at zero or weak external magnetic field strength.Then adiabatically boost the magnetic field strength to aboveB=0.5 T and keep the system still at low enough temperature.Finally in thermal equilibrium,we get the thermal equilibrium state highly entangled.

5.Discussion and conclusion

The degree of entanglement is different in different frames.A direct calculation shows that the complete set of commuting observables should be{?L2,?L3,?L′3, ?S2,?S3}in space-fixed frame{e1,e2,e3},and the Hamiltonian is

One can solve this eigen problem following the same procedure in this paper.When our model is solved in the spacefixed frame,the entanglement of the ground state and the first excited state is shown in Fig.5,which is qualitatively different from that in Fig.4(a).It is the global transformation between the two sets of bases that induces the entanglement variation.The difference in entanglement for the same states comes from the fact that the degrees of freedom being entangled we consider are different in the two sets of bases.This is consistent with physical interpretation that in the space-fixed frame strong enough magnetic field makes the spin mainly occupying|1,-1〉in the low energy states.Then from the view point in space-fixed frame,boosting magnetic field strength just results in opposite effect, disentanglement, compared with the view in the body-fixed frame.

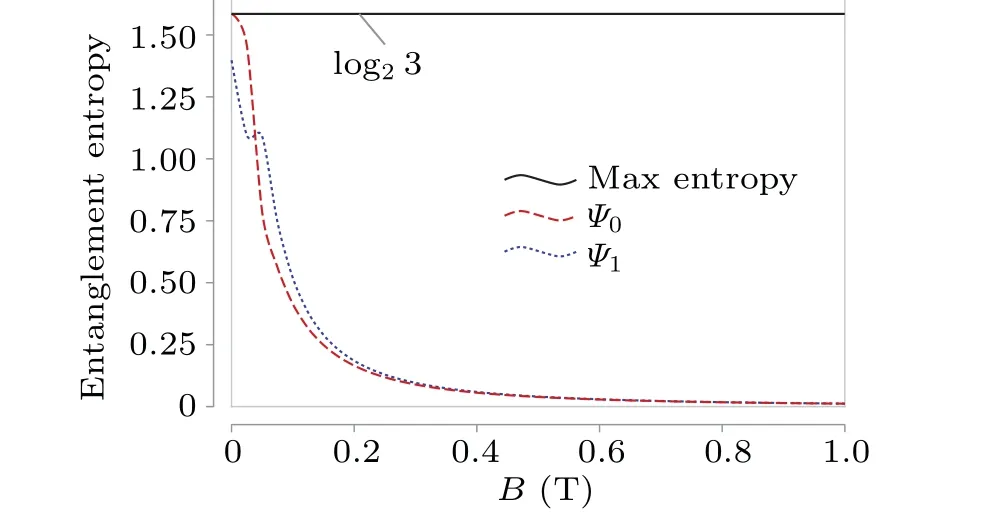
Fig.5.The entanglement entropy of the ground state and the first excited state solved in the space-fixed frame with cutoff Lmax=4.

We propose a theoretical model to describe a rotating nanodiamond with an embedded NV-center manipulated by a static external magnetic field.While,there are still many challenges that need to overcome to bring the primary theoretical model to practical experiment.For example, the nanodiamonds with NV-are usually charged and would gain magnetic moment through rotating.The inertia moments of such small nanodiamond are not easy to determine.Factors such as gravity,noise of the environment,the trap potential and so on need to be studied in more practical situation.And the detection of entanglement is usually very tough such as tomography of the state and entanglement witness.While, indirect detection by reading the spin state and scanning the energy levels employing optically detected magnetic resonance and singlephoton detector may give some possible ways to examine the entanglement information of this system.Indeed, the practical problems which are not considered in this paper need to be further studied.

In our protocol to prepare entanglement, we propose to adiabatically boost the magnetic field strength.Theoretically,however,we do not require the boosting to be adiabatic,a sudden change of the magnetic field strength may also work after a much longer equilibrium time.

In conclusion,we explore the entanglement properties of a rotating nanodiamond with an embedded NV-center in an external magnetic field in a thermal equilibrium state, which includes the ground state as a special case.We find that the degree of entanglement depends on the degrees of freedom chosen in the two frames.The entanglement between nanodiamond rotation and NV-center spin can be controlled by an external magnetic field and the temperature: larger magnetic field strength and lower temperature result in more entanglement between the rotation and the spin.Our numerical results show that in our system setting when the magnetic field strength is tuned above 0.5 T and the temperature is controlled below 2 mK, the thermal equilibrium state will be an almost maximally entangled state.Thus we propose a theoretical protocol to realize the highly entangled states of the spin–rotation coupled system asymptotically.The entanglement between the spin(a microscopic degree)and the rotation(a mesoscopic degree) is not only of usefulness in quantum coherent control of two or multi quantum degrees of freedom,but also of interest in fundamental problems of quantum mechanics such as detection and utilization of quantum rotation of nanoparticles to explore the border between quantum world and classical world.[34]

Appendix A:D-matrix and Euler rotations

In this appendix, we give some details of theD-matrix of Euler rotations.We have chosen{e1,e2,e3}to represent the space-fixed frame and{e′1,e′2,e′3}the body-fixed frame.In the view of passive rotations, we considere′iis rotated toeiby rotation operator ?R, i.e.,ei= ?Re′i=∑3j=1Rjie′j, whereRji ≡e′j·ei.While in the view of active rotations,we usually define the rotation operator ase′i= ?Qeiwhich maps a vectoreito a new vectore′iin the same frame.It is clear to see that ?R= ?Q-1which usually gives the inverse relation of passive and active views of the same rotation transformation.In our paper,we choose the passive view on account of the two coordinate frames.We choose Euler angles{α,β,γ}to represent the rotation from space-fixed frame{e1,e2,e3}to body-fixed frame{e′1,e′2,e′3},which are shown in Fig.2.

According to quantum mechanics, the generator of ?Ris angular momentum ˉh?L, especially in the space-fixed frame,[?Li,?Lj]=i∑k εijk?Lk, wherei,j,k ∈{1,2,3}with ?Li ≡ei· ?Landεijkis an antisymmetric tensor withε123=1.Let ?Dbe the representation of the rotation operator ?Rin Hilbert space, we have

Appendix B:Convergence tests

In this appendix,we display the convergence tests of the cutoff of maximum angular momentumJmaxin our numerical calculation.

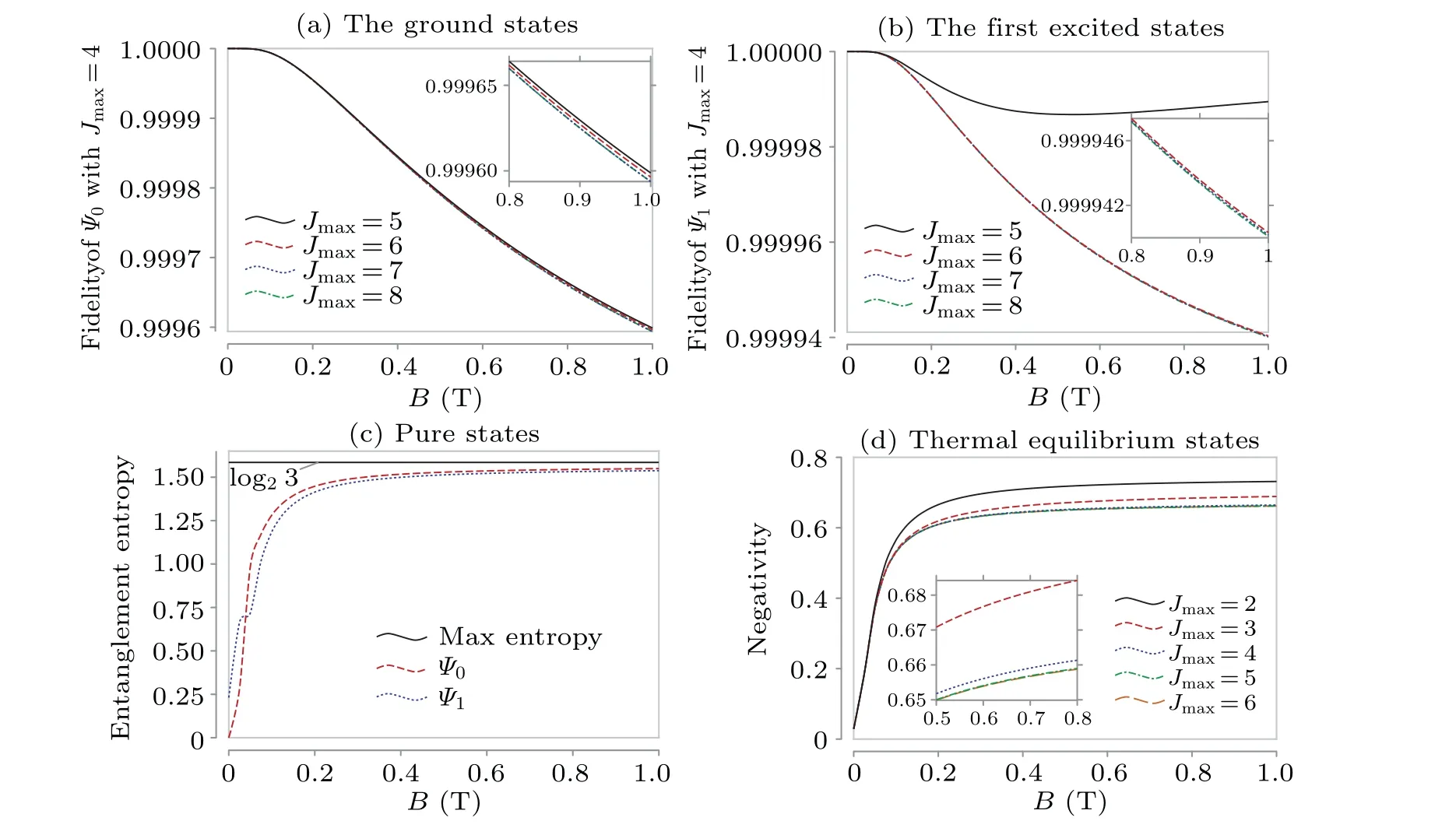
Fig.B1.The fidelity between the(a)ground states((b)1-st excited states)of Jmax =4 and Jmax ∈{5,6,7,8}.(c)The entanglement entropy with cutoff Jmax=8.(d)The negativity of the thermal equilibrium states with different cutoff Jmax ∈{2,3,4,5,6}at temperature T =10 mK.

As a comparison with Fig.4(a)which has cutoffJmax=4,a cutoff ofJmax=8 is shown in Fig.B1(c).For the thermal equilibrium states,we check their negativity with several cutoffJmax∈{2,3,4,5,6}at temperatureT=10 mK which is shown in Fig.B1(d).It is clear to see that the negativity is convergent forJmax≥4.

Acknowledgements

Project supported by the National Key Research and Development Program of China (Grant Nos.2021YFA0718302 and 2021YFA1402104), the National Natural Science Foundation of China(Grant No.12075310),and the Strategic Priority Research Program of Chinese Academy of Sciences(Grant No.XDB28000000).