Higher-order topological Anderson insulator on the Sierpi′nski lattice

Huan Chen(陳煥), Zheng-Rong Liu(劉崢嶸), Rui Chen(陳銳),?, and Bin Zhou(周斌),2,?

1Department of Physics,Hubei University,Wuhan 430062,China

2Key Laboratory of Intelligent Sensing System and Security of Ministry of Education,Hubei University,Wuhan 430062,China

Keywords: fractal system,topological insulator

1.Introduction

Fractals are graphs with self-similarity, in which each constituent exhibits the same character as the whole.[1,2]In recent years,theoretical works concerning quantum effects on fractal lattices have been extensively studied, such as Anderson localization,[3–5]electronic[6,7]and optical conductivity,[8]plasmon dispersion relations,[9]and other related topics.[10–14]Despite being embedded in integer dimensional space, a fractal lattice is characterized by a non-integer Hausdorff dimension.[15]Due to its unique characteristics and motivated by the experimental developments,[16,17]the fractal lattices have attracted much attention in recent years.

On the other hand, tremendous efforts have been devoted to the study of topological systems in integer dimensions during the past two decades.[18–21]Nowadays, researchers have extended these topological phases to fractal systems,which allow for new topological phenomena that are impossible in crystals.For example, topological phases in fractals do not possess a well-defined bulk like their crystalline counterparts, but they are able to support topologically protected states on the boundary.[22]Topological phases have been widely investigated in different fractal systems,[23–25]such as the Chern insulator,[26–31]higher-order topological insulator,[32–34]non-Hermitian topological insulator,[35]and topological superconductor.[36,37]The second-order topological insulator (SOTI) in fractals exhibits unique inner corner modes.[32]The Chern insulator in fractals is protected by the robust mobility gap instead of the direct bandgap in conventional topological insulators.[33]In the meantime, topological phases in fractals have been experimentally reported in various systems, such as the Chern insulator[33]and higherorder topological insulator[34,38]in acoustic systems and Floquet topological insulator[22,39]and higher-order topological insulator[24]in photonic systems.

Moreover, the interplay between disorder and dimensionality plays a critical role in the research of topological systems.The disorder-induced topological phase, which is referred to as the topological Anderson insulator (TAI),was first proposed by Liet al.[40]Since then, the TAI phases have been investigated in numerous systems in integer dimensions.[41–58]So far, the TAI phase has been observed experimentally in one-dimensional disordered atomic wires,[59]photonic platforms,[60–62]and a quantum simulator on a superconducting-circuit device.[63]Recently, the TAI phase has been proposed to be realized in an electric circuit.[64]However, it is worth highlighting that the disorder effect on fractal systems remains an unexplored territory.

Here, we investigate the disorder-induced topological phase transition on the Sierpi′nski lattice, which is one of the best-known examples of a fractal system.Depending on the topological mass,the fractal system supports a normal insulator(NI)phase with a zero topological index and a SOTI phase with a quantized quadrupole moment.We find that the SOTI on the Sierpi′nski lattice is robust against weak disorder.Surprisingly,we reveal that disorder can induce a phase transition from the NI phase to the SOTI phase,indicating the occurrence of the higher-order TAI phase in the fractal system.Moreover,the disorder-induced phase is further confirmed by calculating the energy spectrum and the corresponding probability distribution.

This work is organized as follows.We give a brief description of the Sierpi′nski lattice in Subsection 2.1,introduce the tight-binding Hamiltonian in the fractal system in Subsection 2.2,and adopt the quadrupole moment to characterize the system in Subsection 2.3.Then we demonstrate that the topological nature of the system can be captured by the quadrupole moment in Section 3.1, discuss the disorder effects on the fractal system in Subsection 3.2, and show that the disorderinduced phase transitions can be further confirmed by calculating the energy spectrum and the probability distributions in Subsection 3.3.Finally, we make a summary and a brief discussion in Section 4.

2.Model and method

2.1.Sierpi′nski lattice

The Sierpi′nski lattice can be regarded as the lattice obtained after the manufacture of defects following certain laws on a square lattice.[26,27]The initial unit contains eight sites(the green sites in Fig.1).This unit is replicated 8 times to obtain the structure of the next generation, which contains an inner hole without lattice site (the blue sites in Fig.1).This operation is repeated to obtain the red sites in Fig.1.Each iteration makes the number of lattice sites become eight times that of the previous generation by copying and moving.In this way, we can easily describe the fractal lattice of a Sierpi′nski carpet.For a certain generationf,the site numberN=8f.For the iterationsf ?1,we obtain an approximation of the Sierpi′nski carpet with fractional Hausdorff dimensiondH=ln8/ln3?1.89.

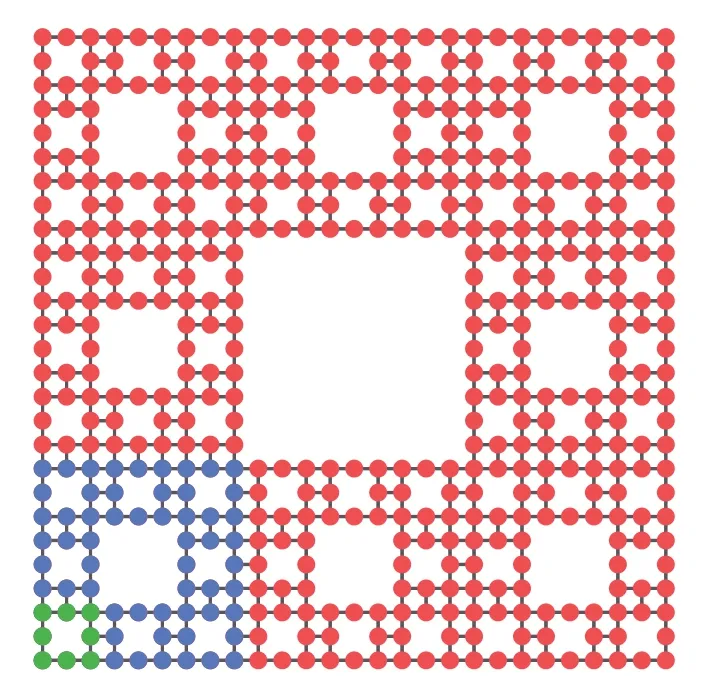
Fig.1.Schematic illustration of the Sierpi′nski lattices.Here,the green,blue,and red sites make up the first,second,and third generations with the site numbers 8,64,and 512,respectively.

2.2.Hamiltonian

The tight-binding Hamiltonian of a quadrupole insulator on the Sierpi′nski lattice has the following form:[32,65]

where

describes a first-order topological insulator protected by timereversal symmetry.Here,the long-range hopping between two different sites is considered andl(rjk)= e1?rjk/r0corresponds to the spatial decay factor of hopping amplitudes, whererjkis the lattice spacing between sitesjandk, andr0is the decay length.φjkis the polar angle between sitesjandk.σ1,2,3andτ1,2,3are the Pauli matrices acting on the spin and orbital spaces,respectively.σ0andτ0are identity matrices.t1andt2denote the hopping amplitudes.is the creation operator at sitejdetermined by spin direction↑,↓and orbital indexα,β.The second part

is the Wilson mass term,which breaks the time-reversal symmetry.The Wilson mass term hybridizes and then gaps out the counter-propagating gapless edge modes of the system.Moreover,H2causes the sign of the domain-wall mass to flip four times under 2πrotation,which breaks four-fold rotational symmetryC4.[66–68]In the clean limit,the HamiltonianHrespects the combined symmetryC4T,[32,65]whereT=s2τ0Kis the time-reversal symmetry andKis the complex conjugation.For the rest of the discussion,we setr0=1,t1=t2=1,g=1.The last term

depicts the Anderson-type disorder.Ujis a set of uniform random numbers distributed within the range of [?W/2,W/2],withWbeing the disorder strength.

2.3.Quadrupole

We adopt the quadrupole moment to characterize the fractal system,which is given by[32,65]

It should be noticed thatQxyis a gauge-dependent quantity for a finite-size fractal system and becomes gaugeinvariant in the thermodynamic limit.[32]In this sense,strictly speaking,Qxyis only available for an infinite system.However, we find that for a large-enough system withf=3,Qxyis able to capture the topology nature of the system(see Subsection 3.1 below).Therefore, in this work, we still employQxyto characterize the topological properties of the finite-size system.

3.Numerical investigation

In this section,we first show that the quadrupole momentQxycan indeed capture the topology nature of the fractal system.Subsequently,we investigate disorder effects on the fractal system.Moreover, all the numerical calculations are performed on the third generation of the Sierpi′nski lattices.

3.1.Clean limit

We start with the case of clean limit, i.e.,W=0.Figures 2(a)–2(d) show the energy spectrum and the corresponding probability distribution of the fractal system on the Sierpi′nski lattices withm=0.The system hosts corner modes residing on both the outer corners[Fig.2(b)]and the inner corners[Fig.2(c)].Moreover,it is found that the system is characterized by a quantized quadrupole moment withQxy=0.5.The quantized topological index and the emergence of the corner models confirm that the system corresponds to a SOTI phase.

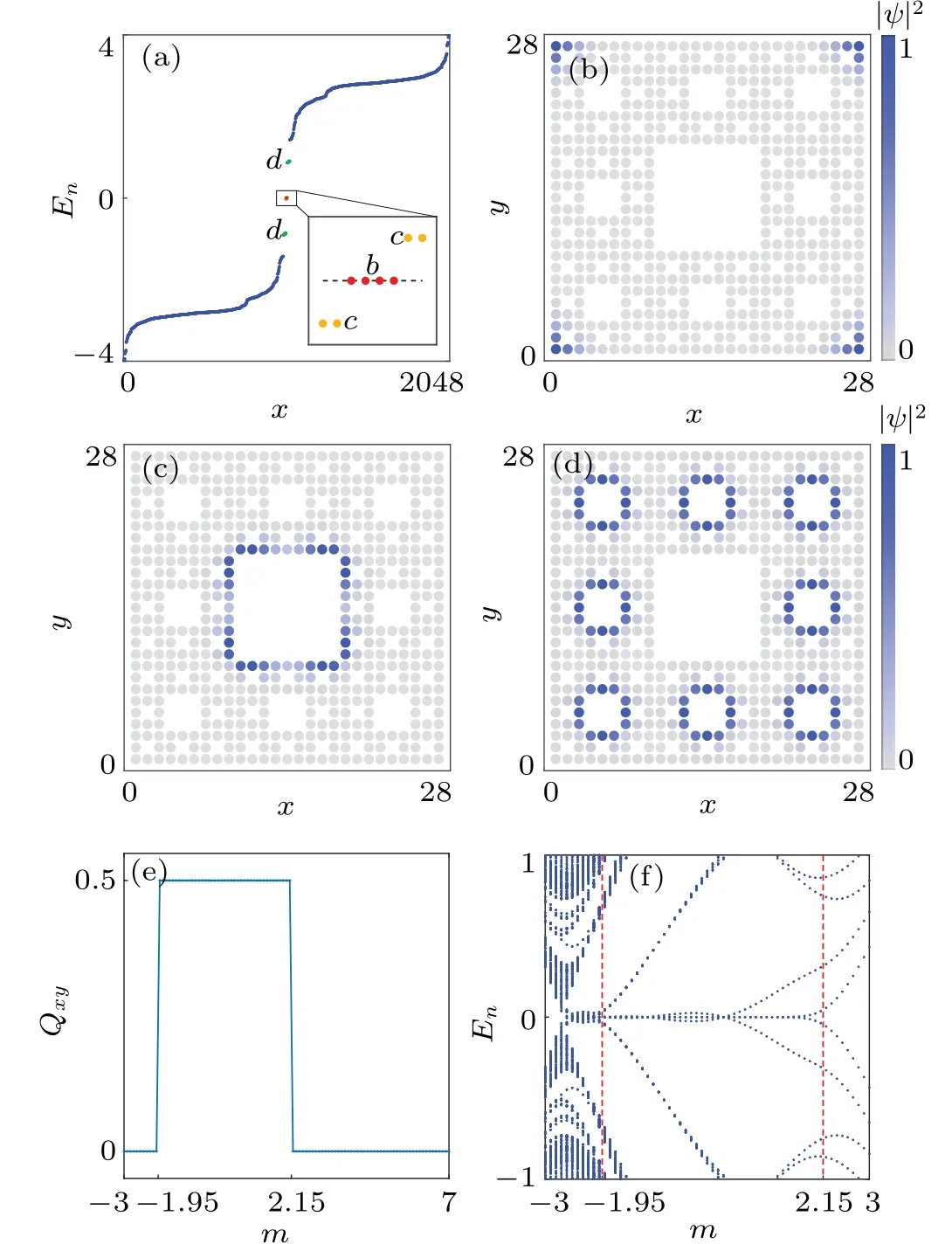
Fig.2.(a) Energy spectrum of the fractal system constructed on the third generation of the Sierpi′nski lattice with m=0.Panels (b), (c),and(d)show the probability distributions of the red,yellow,and green energy modes labeled in(a),respectively.(e)The quadrupole moment Qxy and(f)the energy spectrum as functions of the parameter m.

Moreover, the energy of the four outer corner modes is nearly zero[the red points in Fig.2(a)]and the four inner corner modes open a tiny energy gap in the spectrum[the yellow points in Fig.2(a)].In addition, there exist 32 energy modes inside the bulk gap [the green points in Fig.2(a)], with their probability distributions localized around a series of secondary inner boundaries[Fig.2(d)].

Figures 2(a) and 2(b) show the quadrupole momentQxyand the corresponding energy spectrum as functions of the parametermon the fractal system,respectively.We find that the SOTI phase characterized byQxy=0.5 always hosts four zeroenergy inner corner modes.The other in-gap localized states are not that stable compared to the four outer corner modes.Therefore,we show that the quadrupole momentQxycan capture the topology nature of the fractal system.

3.2.Disorder effects

Now, we study the disorder effects on the fractal system.For the SOTI phase withQxy=0.5, the results are as expected [Fig.3(a)].With increasing disorder strengthW,Qxykeeps the quantized value untilWexceeds certain values.Therefore, similar to the previous studies on disordered topological systems,[40,41]the topological nature of the SOTI phase in the fractal system is also robust against weak disorder.Further increasing the disorder strength,the quantizedQxyis suppressed by disorder,then gradually decreases and finally collapses to zero.

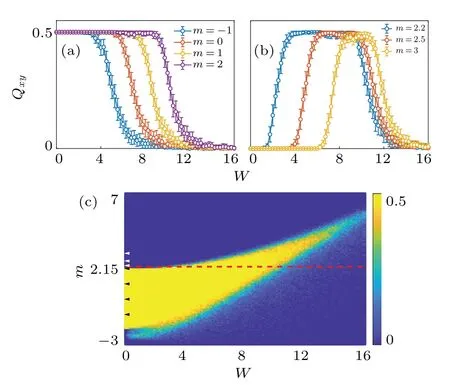
Fig.3.The quadrupole moment Qxy as a function of the disorder strength W for (b) m=?1, 0, 1, 2 and (c) m=2.2, 2.5, 3, respectively.The error bar represents the standard deviation of 500 samples.(c)The quadrupole moment Qxy calculated in the(W,m)plane.In(c),each data point is averaged on 50 independent disorder configurations.

In the clean limit,the NI phase is characterized byQxy=0[Fig.3(a)].With increasing disorder strength, the disorderaveraged quadrupole momentQxyincreases and then forms a quantized plateau withQxy=0.5.The quantized plateau is observed for a certain range of disorder strength,and it decreases and finally disappears with increasing the disorder strength.The zero fluctuation of the quantized plateau indicates that it corresponds to a disorder-induced SOTI phase.Moreover,we plot the diagrams of the system as a function ofmandWin Fig.3(c).The disorder-induced topological phase transitions can be observed more clearly.

3.3.Disorder-averaged energy spectrum and probability

Here, we show that the above disorder-induced phenomenon can be further confirmed by checking the disorderaveraged spectrum and the corresponding probability distribution.

Figure 4(a)shows the disorder-averaged energy spectrum as a function of the disorder strengthWform=0.In the clean limit (W=0), the system corresponds to a SOTI and hosts eight nearly-zero-energy modes with their probability distributions localized on the four outer corners and the four inner corners[Fig.4(b)].With the increasing disorder strength,the bulk gap diminishes and vanishes for aboutW=6.This is in accordance with the results shown in Fig.3(a), where the quantizedQxyalso starts to collapse whenW= 6.Further increasing the disorder strength, the four inner corner modes first disappear[Fig.4(c)],followed by the disappearance of all corner modes[Fig.4(d)].

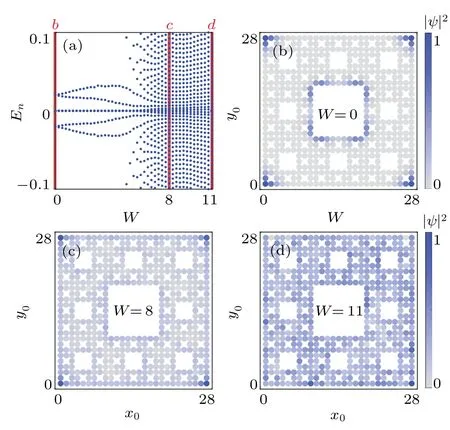
Fig.4.(a) The energy spectrum as a function of the disorder strength W for the SOTI phase with m=0.(b)–(d)Disorder-averaged probability distribution of the middle eight energy modes with disorder strength W =0, 8, and 11, respectively.Here, each data is obtained after averaging on 500 random disorder configurations.

Figure 5(a)shows the disorder-averaged energy spectrum as a function of the disorder strengthWform=2.2.In the clean limit (W=0), the system corresponds to an NI and no corner modes appear[Fig.5(b)].With the increasing disorder strength,the bulk gap decreases and vanishes for aboutW=4.This is in accordance with the results shown in Fig.3(b),where the quantizedQxyemerges whenW=4.Further increasing the disorder strength, the eight corner modes appear [Fig.5(c)]and finally are suppressed by strong disorder[Fig.5(d)].

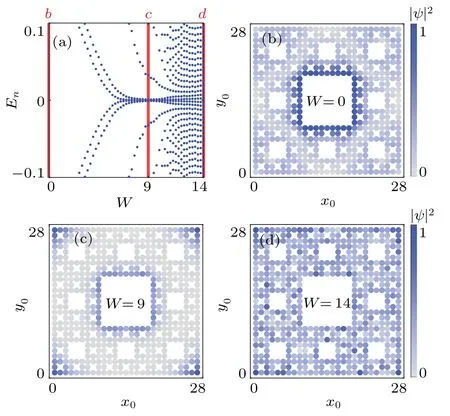
Fig.5.(a) The energy spectrum as a function of the disorder strength W for the NI phase with m=2.2.(b)–(d)Disorder-averaged probability distribution of the middle eight energy modes with disorder strength W =0, 9, and 14, respectively.Here, each data is obtained after averaging on 500 random disorder configurations.

4.Conclusion

In this work, we study the disorder effects on a fractal system constructed on the Sierpi′nski lattice.We show that SOTI phase on the fractal system is robust against weak disorder.Moreover, we reveal a disorder-induced SOTI phase characterized by an emergent quantized quadrupole moment withQxy= 0.5.Finally, the disorder induced phenomena on the fractal system are further confirmed by checking the disorder-averaged energy spectra and the corresponding probability distributions.In crystals, disordered-induced higherorder topological phase manifests localized states at external corners.[57,58]However, in fractal lattices, the disorderinduced phases manifest localized states at both internal and external corners.This property represents a unique characteristic of the disorder-induced second-order topological phase in the fractal system.

We expect that the disorder-induced SOTI phase in the fractal system can be experimentally realized in some metamaterials in the future.The SOTI phases in fractal systems have been experimentally observed in both the acoustic[34,38]and the photonic[24]systems.On the other hand, the disorder effects have been introduced in both the acoustic[69,70]and the photonic[60–62]systems.The above experiments offer the possibility of future experimental realization of our proposal.

Acknowledgements

R.C.acknowledges the support of the National Natural Science Foundation of China (Grant No.12304195) and the Chutian Scholars Program in Hubei Province.B.Z.was supported by the National Natural Science Foundation of China (Grant No.12074107), the program of outstanding young and middle-aged scientific and technological innovation team of colleges and universities in Hubei Province(Grant No.T2020001), and the innovation group project of the Natural Science Foundation of Hubei Province of China (Grant No.2022CFA012).Z.-R.L.was supported by the Postdoctoral Innovation Research Program in Hubei Province (Grant No.351342).