Effects of confining pressure and pore pressure on multipole borehole acoustic field in fluid-saturated porous media
Zhi-Qiang Zhao(趙志強(qiáng)), Jin-Xia Liu(劉金霞), Jian-Yu Liu(劉建宇), and Zhi-Wen Cui(崔志文)
College of Physics,Jilin University,Changchun 130012,China
Keywords: confining pressure,pore pressure,fluid-saturated porous media,multipole borehole acoustic field
1.Introduction
In actual oilfield wells, especially in the reservoir target layers, the medium is a porous medium saturated with fluids.Moreover,in the exploration and development of oil storage,in-situstress is commonly existent.Thein-situstress may arises from prolonged sedimentation or complex geological formations.It could also result from oilfield development activities such as drilling and water injection.[1]Thein-situstress in the reservoir is triggered off partly by the fluid in the pore of the reservoir, called the pore pressure, and partly by the rock skeleton of the reservoir,called the effective stress.[1]The stress in fluid-saturated porous media plays an important role in the realization of safe drilling and efficient reservoir exploitation.During drilling, higher pore pressure can lead to well control accidents, which is one of the major drilling hazards worldwide.And accurate pore pressure prediction is very important for successful drilling operations.[2]Furthermore, gaining an insight into the state ofin-situstress provides a more comprehensive understanding of gas exploration and development,[3–5]enhanced oil recovery techniques,[6,7]wellbore stability,[7,8]and reservoir management.[9,10]
The elastic wave dynamic theory describing fluidsaturated porous media was initially established by Biot.[11–13]Biot[14]adopted the nonlinear continuum theory to first investigate the acoustoelastic theory for the fluid-saturated porous media and only presented the equations of motion for the fluidsaturated porous media under the initial stress.Grinfeld and Norris[15]proposed general theory of small dynamic motion superimposed upon large static deformation for isotropic fluidfilled poroelastic solids,extending the acoustic–elastic theory applicable to single-phase media to fluid-saturated porous media.Baet al.[16]improved the fluid-saturated porous media theory given by Grinfeld and Norris[15]by considering the nonlinear term of static strain.Wang and Tian[17]utilized the finite deformation theory of continuum and pore elastic theory to give the equation of motion of small disturbance wave field superimposed on nonlinear shape variants caused by static stress in fluid-saturated porous media.Maet al.[18]derived the equation of motion of fluid-saturated porous media,adapted to large static deformation and superimposed disturbance wave field.According to the Pade approximation,Fu B Y and Fu L Y[19]extended the acoustic–elastic theory to the case of higher effective stress,which was verified experiment.Fu B Y and Fu L Y[20]introduced the two-pore model into the traditional acoustic–elastic model of fluid-saturated porous media, and found that the experimental results are better in the case of low effective pore pressure.Quet al.[21]experimentally measured the third-order elastic modulus of fluidfilled porous rocks under uniaxial stress.Kanaun[22]investigated the effect of the pressure of fluid injected into porous media under quasi-static conditions.Liuet al.[23]studied the influence of the nonlinear parameters of fluid-structure coupling on acoustic field in porous media.Liuet al.[24]improved and modified the dynamic equation of static deformation with small perturbations of porous media,with the viscosity term and the dispersion taken into account.The study of acoustic wave propagation in fluid-saturated porous media is of great significance in evaluating reservoir properties by using acoustic logging.Utilizing the Biot theory,Rosenbaum[25]investigated the propagation of acoustic field in boreholes surrounded by porous media, named the Biot–Rosenbaum theory.Wang and Dong[26]rigorously used the theory of elastic waves in porous media to theoretically solve the radiated acoustic field surrounded by fluid-saturated porous media in an open borehole.Schmittet al.[27]and Schmitt[28]studied the formation of radially layered fluid-saturated porous media, where both the elasticity and permeability of the formations exhibit anisotropic characteristics.Zhanget al.[29]employed the Biot two-phase medium model to simulate oil reservoirs and systematically conducted theoretical derivation,mode decomposition analysis, and full-wave computation of the acoustic wavefield excited by multipole sources in the borehole.Zhang and Wang[30]introduced an analytical perturbation method to address the problem of multi-source acoustic well logging in transersely isotropic two-phase media.Building upon the BISQ model, Cuiet al.[31]studied the dispersion and attenuation of elastic waves in non-Newtonian fluidsaturated porous media.Guan and Hu[32]employed the timedomain finite difference algorithm to simulate acoustic well logging responses to horizontally layered porous formations.Heet al.[33,34]employed three-dimensional finite-difference simulations to model inclined layered porous formations and porous elastic formations with anisotropic magnetic permeability.Penget al.[35]analyzed the acoustic wave propagation and wellbore acoustic fields in non-uniform porous media saturated with viscous fluid.
The above studies did not cover the simulation research of borehole acoustic fields in fluid-saturated porous media under the influence of stress,based on the theory of acoustoelasticity in fluid-saturated porous materials.Therefore, this work primary focuses on the refinement of the existing theory of acoustoelasticity in fluid-saturated porous media and the research of borehole acoustic field in fluid-saturated porous media under reservoir stress conditions.
The rest of this paper is organized as follows.In Section 2,the equation of borehole acoustic field in fluid-saturated porous media under pore pressure and confining pressure is derived.In Section 3,numerical results are presented to show the effects of confining pressure and pore pressure on multipole borehole acoustic field in a fluid-saturated porous media.Finally,some conclusions are drawn in Section 4.
2.Theoretical formula
In this section,based on the dynamic equations for static deformation of porous media with small perturbations, given by Liuet al.,[24]the motion equations of fluid-saturated porous media under pore pressure and confining pressure are derived and an expression for velocity and stress is given.In the cylindrical coordinate system,the field equations of open hole stimulated by multiple sources in fluid-saturated pore formation under confining pressure and pore pressure are derived.
2.1.Field equation for fluid-saturated porous media under confining and pore pressure
This subsection mainly derives the field equations of fluid-saturated porous media under confining pressure and pore pressure.The confining pressure and pore pressure in the media do not change the isotropic properties of the media.This subsection refers to the research work of Liuet al.[24]and gives the field equation under confining pressure and pore pressure as follows:
whereuis the displacement of solid phase.w=?(uf?u)is the seepage displacement.ufis the average fluid displacement.?is the porosity.τis the stress tensor,Pis the pore fluid pressure,andIis a unit vector.Here,the equivalent elastic moduli are denoted byH',M',C', andG'.According to the work of Liuet al.,[24]one can obtain the equivalent elastic moduli related to stress as follows:
whereH,M,C, andGare four independent elastic constants of fluid-saturated porous media.H,M,andCcan be expressed as solid bulk modulusKs, pore fluid bulk modulusKf, frame bulk modulusKb,frame shear modulusG,and porosity?.
The symbols Δ in Eq.(2), respectively, represent the change of porous elastic modulusH,M,C,andG,caused by the confining pressure and pore pressure.
whereλc=Kb?2/(3G)+α2Mis the parameter of Biot.v'1,v'2,andv'3are the third-order elastic constants of porous elastic media.When there is no fluid in the media, they correspond to the third-order elastic constants in the elastic mediav1,v2andv3.[36]γ2,γ3, andγare the nonlinear constants of the coupling between a fluid and a solid.γ1is a nonlinear constant associated with the fluid phase.es=(Pc+αPp)/Kb,ζs=(Pp+αMes)/Mare the static deformations caused by the confining pressure and pore pressure which satisfy the linear stress–strain relationship.[24]ThePcandPprepresent the confining pressure and pore pressure,respectively.
The corresponding equation of motion can be written as
where the superscript refers to the derivative with respect to time,ρis the density of porous media and expressed asρ= (1??)ρs+?ρfwithρsandρfbeing the solid density and pore fluid density,respectively,?being the porosity,?ρ=jη/(ωk(ω))andk(ω)=k0/(1?jωEρfk0/(η?)),withηbeing the dynamic viscosity of pore fluid,kthe permeability,ωthe angular frequency, andEthe tortuosity.Here, the displacementsuandware assumed to vary with time according to e?jωt.By substituting Eq.(1) into Eq.(5), the elastic dynamic equation withuandwas the basic quantities can be obtained as follows:
Unlike Boit’s kinetic equation,[37]here the elastic moduliH',M',C', andG'depend on confining pressure, pore pressure,and the third-order elastic modulus.A displacement potential is introduced, which is similar to the solution of plane waves in Biot fluid-saturated media[38]
whereΦandψare the compressional and shear wave displacement potentials, respectively,apandasare both the ratio of seepage displacement(complex)amplitude to solid displacement (complex) amplitude.The subscripts p and s represent P-waves and S-waves, respectively.Let plane solutionΦ=Apej(lx?ωt)andψ=Asej(lx?ωt)whereApandAsare amplitude of compressional wave and shear wave,respectively,ldenotes the wave number.Shear waves(ls=Ssω)and two types of compressional waves(lpf=Spfωandlps=Spsω)can be obtained by substituting Eq.(7)into Eq.(6).Si(i=pf,ps,and s)denotes slowness.
whereb= (ρM'+ ?ρH'?2ρfC')/(H'M'?C'2).SpfandSpsdenote slowness of the fast and slow P-waves, respectively.Equation (8) is the relationship between the slowness of the fast and the slow P-wave and confining pressure and pore pressure.Shear waves slownessSscan be written as
Equation (9) is the relationship between the slowness of the S-wave and confining pressure and pore pressure.At the same time,the ratio of seepage displacement amplitudes of the fast and slow P-waves to solid phase displacement amplitudes can be obtained to be
whereSi(i=pf,ps)is slowness.
The ratio of seepage displacement amplitudes of the Swaves to solid phase displacement amplitudes can be obtained to be
2.2.Equations of borehole acoustic field in fluid-saturated porous media under pore pressure and confining pressure
Because the fluid-saturated porous media are still isotropic under the action of pore pressure and confining pressure, the acoustic field formula in the borehole under the action of confining pore pressure is similar to the classical fluidsaturated porous formation.[29]The acoustic field in the borehole fluid is expressed as
wheren=0,1,2 represent monopole,dipole,and quadrupole source, respectively; Inand Knare then-th order modified Bessel function of the first kind and second kind,respectively;kr=(k2z ?k2f)1/2is the radial wave number of the fluid;kzis the axial wave number;kf=ω/Vfis the fluid wave number of borehole;ωis the angular frequency;Vfis the speed of sound in the borehole fluid;εnis the constant related to the sound source in the direct field.When the sound source is a monopole source (n=0),εn=1; when the sound source is multipole (n >0),εn=2.An1(kz,ω) is the reflection coefficient in the reflection field,which is determined by the boundary conditions.The displacement component and stress are expressed as
In Eqs.(13) and (14), the factoris omitted.The shear wave vectorΨin Eq.(7)can be further written into two terms.The compressional wave potentialΦ, horizontal polarized shear wave (SH wave) potentialχand vertical polarized shear wave(SV wave)potentialΨare introduced for the displacement of fluid-saturated porous media under external confining pressure and pore pressure.
whereΦpfandΦpsare the fast-wave potential and slow-wave potential,respectively;aps,apf,andasare the ratio of seepage displacement amplitudes in Eqs.(10) and (11).By substituting Eq.(15) into Eq.(6) and expanding it in the cylindrical coordinate system, the solution of displacement potential can be obtained to be
wherei=pf,ps represent the fast wave and slow wave.vi=are the radial imaginary wave numbers of fast and slow P-waves and S-waves, respectively.Unlike classical Biot fluid-saturated media,[12]here the fast,slow, and shear waves depend on the confining pressure and pore pressure.According to the boundary condition atr=r0of borehole
we obtain the matrix equation with unknown coefficients in the following form:
wheremij(i,j=1, 2, 3, 4, 5)are the elements of the matrix,b1,b2,andb3are given in Appendix A.The dispersion equation of the guided waves can be obtained by setting the determinant of the coefficient matrix in Eq.(18)to zero and the excitation intensity can be obtained from the pole residue.The reflection coefficientAn1can be obtained by solving Eq.(18),and the full wave field under confinement and pore pressure can be obtained from Eq.(14) by using the real axis integral and Fourier transform.
3.Numerical simulation
In this section, the effect of pore pressure and confining pressure on the multipole borehole acoustic field in a fluid-saturated porous media are analyzed numerically.The model is shown in Fig.1, and the borehole radius is 0.1 m.The parameters of fluid-saturated porous formation used in numerical simulation are listed in Table 1, where the parameters are selected from Fuet al.’s work.[20]The density and speed of the fluid in the borehole are 1000 kg/m3and 1500 m/s, respectively.At the same time, in the selection of stress, considering the experiments conducted by Fu B Y and Fu L Y[20]and Saroutet al.,[39]the confining pressure and pore pressure applied to the fluid-saturated porous media should meet the conditions:the confining pressure is large and the pore pressure difference between the confining pressure and the fluid in the porous media is greater than 30 MPa, so that the numerical simulation of the classical theoretical model can be consistent with the existing experimental results.
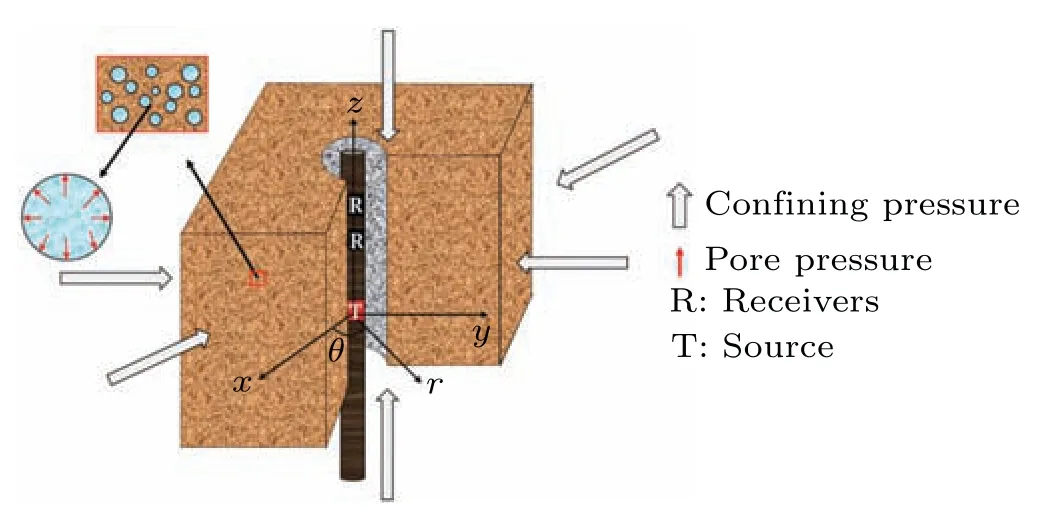
Fig.1.Open hole model,where large grey arrows denote the direction of applied confining pressure and the little red arrow refers to the direction of the applied pore pressure.And in this paper, the confining pressure that compresses into the borehole is defined as negative pressure, and the pore pressure that expands outward in the pore fluid is defined as positive pressure.
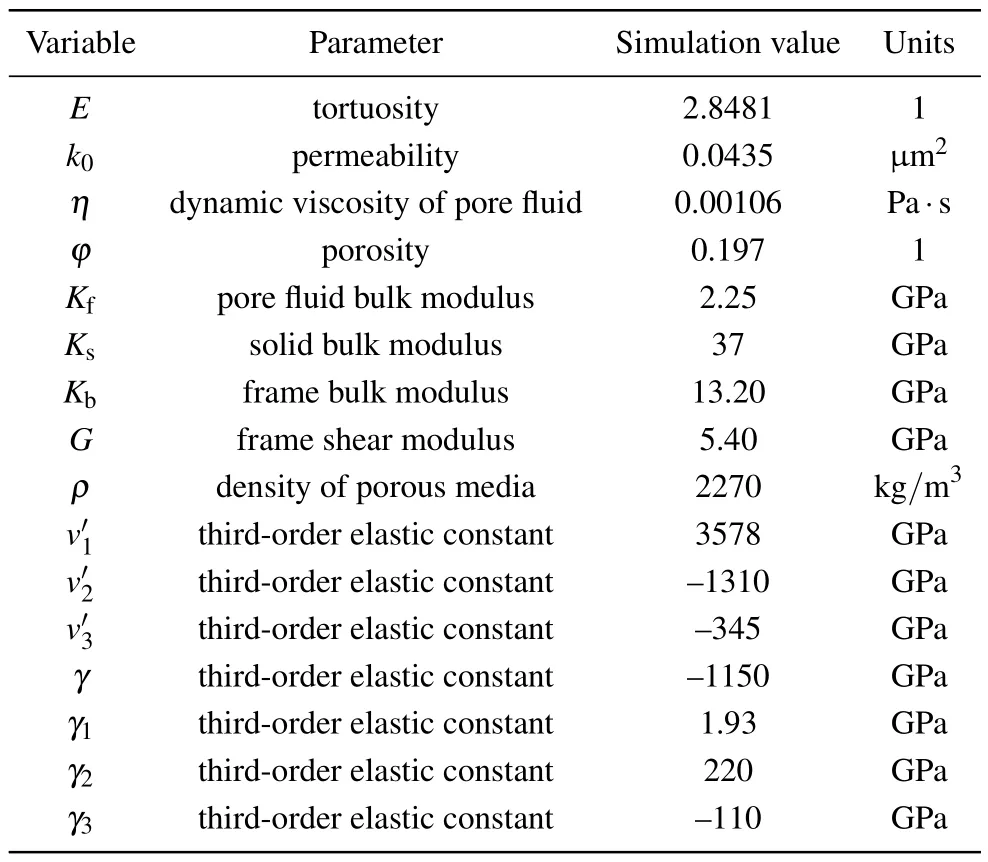
Table 1.Parameters of porous media.
3.1.Dispersion curve
In this subsection,the dispersion curve and excitation intensity of the Stoneley wave, pseudo-Rayleigh wave, flexural wave,and screw wave are calculated from Eq.(18),and the response of the dispersion curve and excitation intensity to pore pressure and confining pressure are analyzed.
Figure 2 shows the curves of (a) dispersion and (b) excitation (b) of Stoneley waves with different confining pressures and pore pressures.In order to show more clearly the response of phase velocity and excitation intensity to pore pressure,the changes in phase velocity and excitation intensity for two different pore pressures at the given confining pressure are shown in Fig.1(c).When the pore pressure and confining pressure are applied with the pressure difference being greater than 30 MPa,the dispersion curve and excitation intensity increase significantly.The group velocity is greater than the phase velocity in the frequency range from 0 kHz to 20 kHz.Under a given confining pressure, the phase velocity, group velocity and excitation intensity decrease as the pore pressure increases.The reason for this phenomenon is that when the pore pressure increases,the strong strain around the compliant pores in porous media greatly reduces the stiffness of the solid phase of porous media.This change induces the nonlinear elastic deformation of the solid phase, which greatly reduces the elastic wave velocity in the solid phase, and leads to the decrease of the guided waves velocity in the porous media.[20]
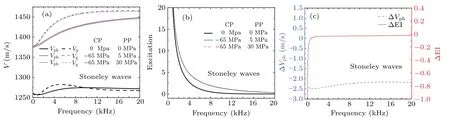
Fig.2.(a) Dispersion, (b) excitation intensity, and (c) changes caused by different pore pressure responses of Stoneley waves; CP and PP denote the confining pressure and pore pressure,respectively.Vph and Vg represent the phase velocity and group velocity,respectively.ΔVph and ΔEI refer to the change of phase velocity (Vph) and excitation intensity (EI), caused by different pore pressures (PP=5 MPa and PP=30 MPa) at the given confining pressure(CP=?65 MPa).
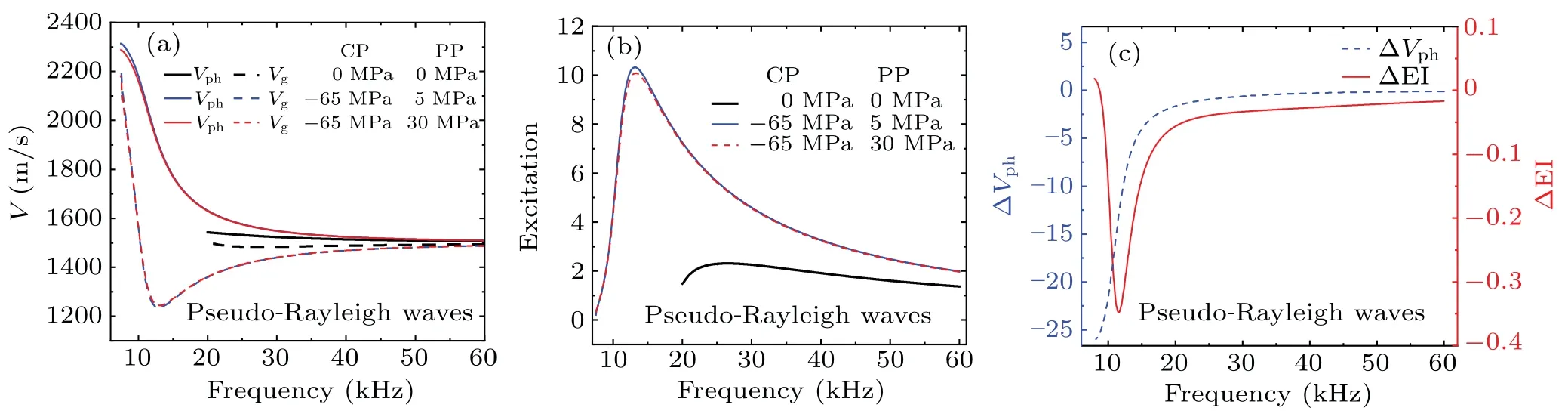
Fig.3.(a)Dispersion,(b)excitation intensity and(c)changes caused by different pore pressure responses of pseudo-Rayleigh waves.The notations in the figure are the same as in Fig.1.
Figure 3 shows the responses of pseudo-Rayleigh waves with different confining pressures and pore pressures.Under the condition of no stress, the shear wave velocity in the fluid-saturated porous media is 1542 m/s, which is close to the acoustic velocity of 1500 m/s in the borehole fluid.After the pore pressure and confining pressure are applied, the properties of the porous media become the harder formation than before.The pseudo-Rayleigh waves can be excited at low frequencies.The phase velocity and excitation intensity also increase significantly.Under a given confining pressure,the phase velocity decreases with pore pressure increasing.The excitation intensity initially increases in a very small frequency range and then decreases at high frequency.In addition,the phase velocity is more sensitive to pore pressure than the group velocity.
Figure 4 shows the responses of flexural waves with different confining pressures and pore pressures.Under the condition of no stress,the flexural wave velocity at very low frequency is close to the shear wave velocity.In the range from 2 kHz to 20 kHz,the phase velocity is greater than the group velocity.When confining pressure and pore pressure are applied, the phase velocity is higher than without stress state,and the maximum value of the excitation intensity becomes bigger and moves towards high frequencies.Under a given confining pressure, the phase velocity and group velocity decrease clearly at low frequency with pore pressure increasing.The excitation intensity of the flexural wave increases at low frequency and then decreases at high frequency with pore pressure increasing at a constant confining pressure.
Figure 5 shows the responses of screw waves with different confining pressures and pore pressures.It can be seen that the response of the dispersion and excitation intensity of the screw waves to the pore pressure are similar to that of the flexural wave.

Fig.4.(a)Dispersion,(b)excitation intensity,and(c)changes caused by different pore pressure responses of flexural waves.The notations in the figure are the same as in Fig.1.
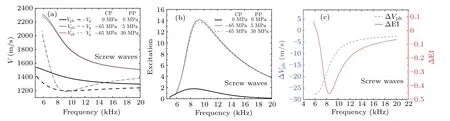
Fig.5.(a)Dispersion,(b)excitation intensity,and(c)changes caused by different pore pressure responses of screw waves.The notations in the figure are the same as in Fig.1.
3.2.Full waveforms
This subsection numerically simulates the full waveforms in the borehole with a sound source at the origin of the cylindrical coordinate system(0,0,0).The receiver is located on the shaft and the distance between the receiver and the source is 5.5 m.The real-axis integration is used to evaluate the waveforms.The different excitation modes of the monopole,dipole and quadrupole source are simulated.And the source pulse functions(t)used in this work is
wheref0andTcare the center frequency and the pulse width,respectively.
Figure 6 shows the full waveforms of the borehole excited by a monopole source with a center frequency of 6 kHz.In the absence of stress,the components of full waves include compressional waves,shear waves and Stoneley waves.After confining pressure and pore pressure are applied,the pseudo-Rayleigh waves appear in the whole wave components.In this case,the arrival times of these waves are significantly reduced.The amplitude of the compressional wave decreases and the amplitude of the guided wave increases with confining pressure increasing.When the confining pressure is given,the amplitudes of these waves do not change significantly and the arrival times of these waves increase as the pore pressure increases.Moreover,we find that the arrival times of the pseudo-Rayleigh waves change much more than those of the Stoneley waves with pore pressure increasing.This is consistent with the dispersion curve responses of Stoneley waves and pseudo-Rayleigh waves.
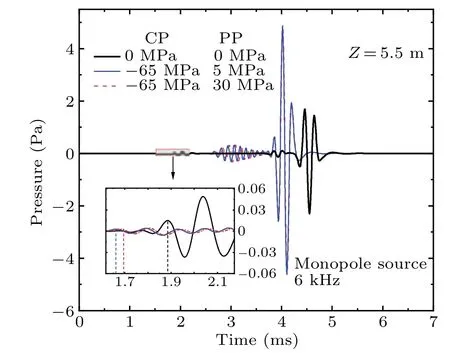
Fig.6.Full waveform response of monopole source,with inset showing linear amplification of the gray area.The amplified part is the waveform of the compressional waves,where the blue dashed line,red dashed line,and black dashed line are the arrival time of the compressional waves at different confining pressures and pore pressures,respectively.
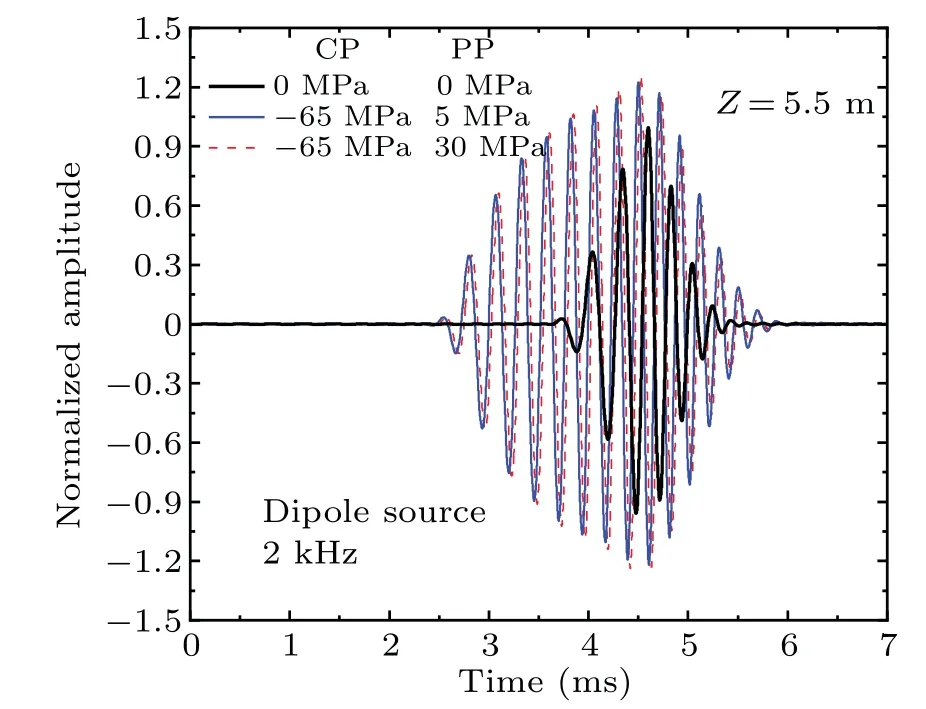
Fig.7.Full waveform response of dipole source, normalized by that without stress.
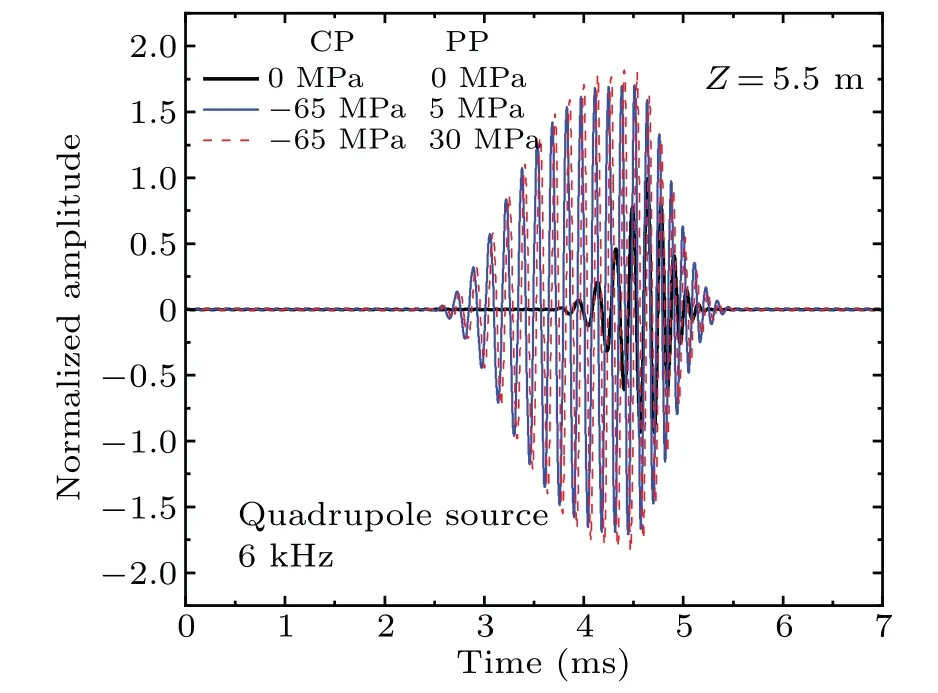
Fig.8.Full waveform response of quadrupole source, normalized by that without stress.
Figure 7 shows the full waveform of the borehole excited by a dipole source.The center frequency of the sound source is 2 kHz.There is the flexural wave components in the full wave.After applying the confining pressure and pore pressure,flexural wave amplitude increases and arrival time decreases.With given confining pressure,the arrival time of flexural waves increases as the pore pressure increases.
Figure 8 shows the full waveform of the borehole excited by a quadrupole source, where the center frequency of the sound source is 6 kHz.It can be seen that the response of the screw waves is similar to that of the flexural waves.
4.Conclusions
In this work, the effects of confining pressure and pore pressure on the multipole borehole acoustic field in a fluidsaturated porous media are investigated.Firstly, the acoustic field equations of fluid-saturated porous media under confining pressure and pore pressure are derived,and the expressions of velocity and stress in the porous media are given.Combined with the borehole boundary conditions,the acoustic field equations of the borehole in fluid-saturated porous media are derived.The responses of dispersion curves and excitation intensities of guided waves (Stoneley, pseudo-Rayleigh, flexural,and screw waves)to confining pressure and pore pressure are analyzed by numerical simulations.The responses of the full waveforms to the confining pressure and pore pressure by the monopole,dipole,and quadrupole sources are also investigated.The numerical results show that the phase velocity,excitation intensity,and full wave amplitude of the guided waves increase significantly under the confining pressure.The amplitude of the compressional waves decreases rapidly as the confining pressure increases.Furthermore,the arrival time of the full waveforms obviously decreases.For a given confining pressure,increasing pore pressure causes the phase velocity of guided waves to decrease.The excitation intensity of Stoneley waves decreases in the whole frequency range,while other guided waves, except Stoneley waves, increases at low frequency and decreases at high frequency.The response of Stoneley waves to pore pressure is smaller than those of other guided waves.The arrival time of the full waveforms slightly increases with pore pressure increasing.The reason is that pore pressure reduces the equivalent elastic modulus of the saturated porous media with constant confining pressure, which reduces the body wave velocity and thus affects the change of the guided waves velocity.The results show that both confining pressure and pore pressure will have an effect on the propagation of elastic waves.In the actual oil and gas exploration, the reservoir formation is generally porous formation,which leads to the necessity of considering confining pressure and pore pressure in exploration.This work may provide some theoretical guidance for evaluating the reservoir properties by acoustic logging in the future.The relationship between the pressure and the guided wave features (velocity and excitation) is revealed.The physical analysis results would help inversions of pressure by the sonic logging responses.This work only considers the case of fluid-saturated porous media subjected to uniform stress, but the actual formation is very complex and subjected to non-uniform stress.Therefore, the response of multipole borehole acoustic field in fluid-saturated porous media under non-uniform stress needs studying further in the future.
Appendix A
The expressions for the matrix elements in Eq.(17)are as follows:
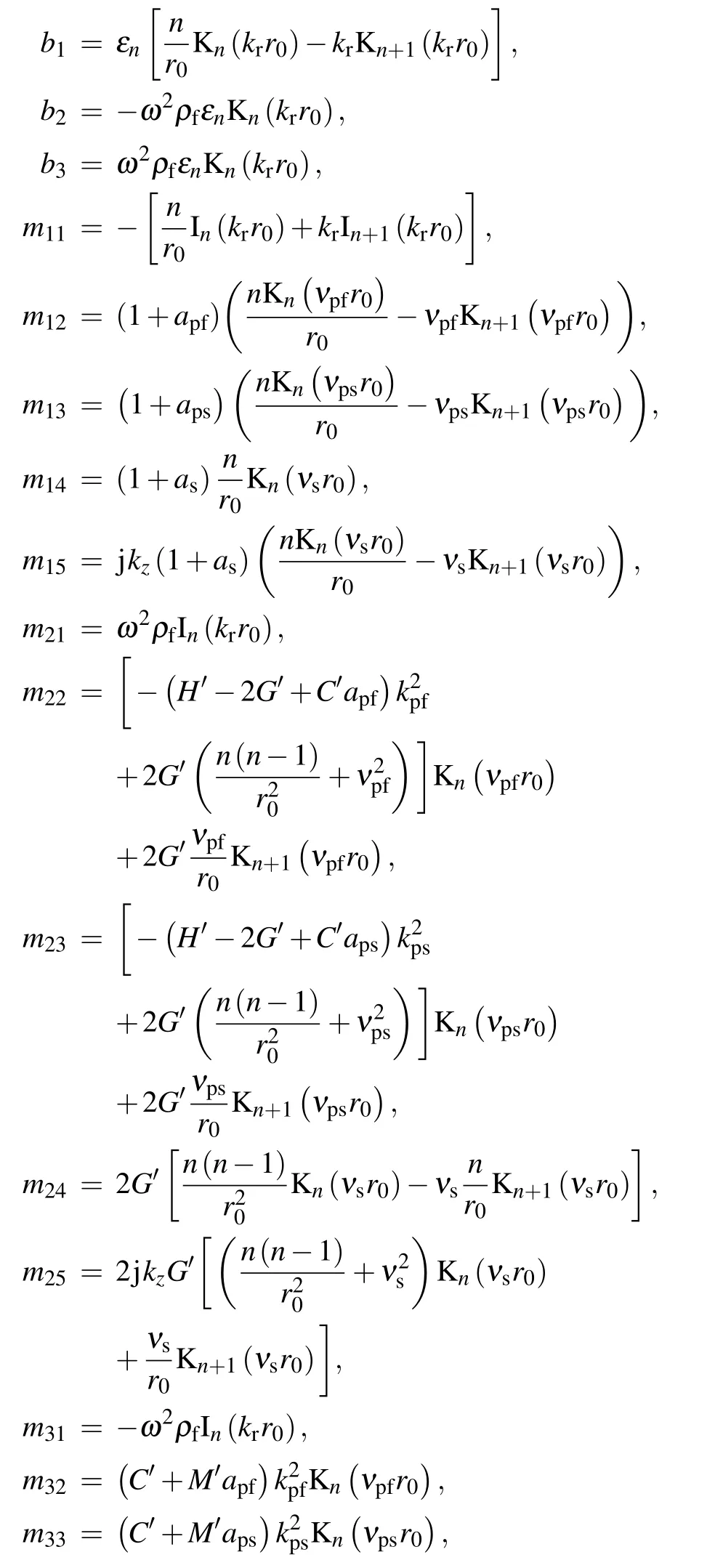
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.42074139) and the Natural Science Foundation of Jilin Province, China (Grant No.20210101140JC).
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

