Realization of arbitrary two-qubit quantum gates based on chiral Majorana fermions*

Qing Yan(閆青) and Qing-Feng Sun(孫慶豐)

1International Center for Quantum Materials,School of Physics,Peking University,Beijing 100871,China

2CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

3Collaborative Innovation Center of Quantum Matter,Beijing 100871,China

4Beijing Academy of Quantum Information Sciences,Beijing 100193,China

Keywords: quantum computation,T gate,CNOT gate,braiding,chiral Majorana fermions

1. Introduction

Facing the dilemma caused by the increasing demand for data processing and the gradual failure of Moore’s law,quantum computation arises to help to break this bottleneck, that is, to compute from the basic quantum-mechanic law rather than stimulate the quantum system in a classical way.[1,2]The power of quantum computation roots in the qubit: the information contained in one qubit, defined as the superposition of two basis states, is much more than that in one classical bit,just 0 and 1;the dimension of computational space grows exponentially as the number of qubits increases due to the exotic entanglement.[3]As one of the computational models,the quantum circuit model takes up the quantum gate to manipulate the qubit based on the original proposal by Benioff that a quantum computer would be constructed by the time evolution of a quantum system.[4]Similar to the XOR and AND gates in the classical computer, a finite set of quantum gates can accurately realize the arbitrary unitary transformation, i.e., the so-called universal quantum gate set{T,H,CNOT}.[5]The design and fabrication of qubits and quantum gates have brought quantum computing into a promising and challenging research field.

Along the way of pursuing a quantum computer, the first step is to fabricate the qubit in a physical system.Among various two-level systems, some with long coherent time have been proposed to serve as a qubit, including photons,[6]trapped atoms,[7,8]quantum dots,[9–11]superconducting Josephson junctions,[12–15]etc. Besides these conventional devices, recent interests in topology claim that a topological system owns a natural advantage of protection against local perturbations, thus opening up a research field called topological quantum computation.[16]The Majorana system,simple but nontrivial,is considered as a potential platform for fault-tolerant topological quantum computation.[17]

In condensed matter physics, Majorana fermions represent a kind of self-conjugate quasiparticle excitations, i.e.,γ?=γ in the operator language.[18]The reality of wave function requires the phase of a Majorana fermion to be either 0 or π. A Majorana fermion is usually regarded as a half of a Dirac fermion,since an ordinary electron and a hole can be reorganized and divided into two real Majorana fermions.[19]In turn,two Majorana fermions form a nonlocal ordinary fermion level with a well-defined occupation number, which is protected by the gap. Besides, Majorana zero modes (MZMs),the zero-energy bound states with non-Abelian statistics,form the degenerate ground state within the gap, which offers the computational space for topological quantum computation.[20]MZMs follow the braiding rule of Ising anyons:after exchanging the positions of two MZMs,one of them acquires a π phase while the other does not,i.e.,γi→γj,γj→?γi.[19,21]The term“non-Abelian” refers that the braiding of γiand γjdoes not commute with the braiding of γjand γk. MZMs have been proposed as qubits,and the fermion parity of MZMs paired in a certain way is defined as the quantum basis states. Braiding MZMs means exchanging their pairing ways,i.e.,rotating the quantum state within the zero-energy degenerate ground state manifold, but keeping the total fermion parity invariant. Due to the global topology, local perturbations do not destroy the ground state,which offers the computational protection as the main advantage but also requires global operations, i.e., the braiding operations, to realize quantum gates corresponding to the Clifford algebra.

Exploring MZMs in theory is both attractive and challenging.[22,23]Kitaev first constructed a toy model containing MZMs as the zero-dimensional end state of a 1D spinless p-wave superconducting nanowire.[24]Despite its difficulty to be realized in experiments, the spinless p-wave superconductor inspires new routines to synthesize the so-called topological superconductor (TSC), which supports MZMs at the boundary or at the vortex. With the development of topological materials[25–28]with strong spin–orbit coupling, Fu and Kane started from a 2D topological insulator, covered it with an s-wave superconductor to induce the pairing potential, and added a ferromagnetic insulator to break the timereversal symmetry so as to trap MZMs at domain walls.[29,30]MZMs also appear at the end of the 1D nanowire with strong spin–orbit coupling, when applied with a perpendicular magnetic field and covered with an s-wave superconductor.[31–33]MZMs can be induced by a small magnetic field in a hollow nanowire sandwiched between two superconductors.[34]MZMs localize at the vortices in the topological superconducting region when 3D topological insulators or 2D electron gas with Rashba spin–orbit coupling are sandwiched by an s-wave superconductor and a ferromagnetic insulator.[29,35]Besides,Tang et al. predicted the existence of the MZMs in some organic molecules(e.g.,DNA)proximity coupled by an s-wave superconductor and under the magnetic field.[36]

Considering the experimental detection of MZMs, one of the most important theoretical proposals points out that the existence of MZMs leads to a transport outcome: a robust and quantized zero-bias conductance peak due to the perfect Andreev reflection.[37]Correspondingly,Mourik et al. in 2012 first detected the anomalous zero-bias conductance peak as the signature of MZMs locating at the end of the InAs nanowire.[38]After that, other experiments observed MZMs bound at the end of ferromagnetic iron(Fe)atomic chains on the surface of superconducting lead(Pb),[39]the vortex of the iron-based superconductor[40]as well as the interface of the helical hinge states of Bi and magnetic iron clusters on the superconducting substrate.[41]Besides, the 4π periodic fractional Josephson experiment provided compelling evidence of the charge parity conservation of MZMs.[42]

Then the question comes that how to braid MZMs in a real physical system and how to realize the topological quantum computation based on MZMs, facing with the difficulty that MZMs are constrained at the end or vortex of TSCs.The T junctions[43]or Y junctions[44]are theoretically proposed to move the MZM one by one by tuning the electric gate or magnetic flux, changing the topology of superconducting regions, evolving the system from one degenerate ground state to another, or pushing one MZM from one end to another end. During such evolution process, the non-Abelian Berry phase accumulates and one of the two MZMs gets a π phase, after completing the braiding process. Moreover, there is a “strange” strategy named as “braiding without braiding”,[45]which does not need to move MZMs but to measure them. When performing a physical measurement on a non-eigen superposition state, this superposition state will collapse into one of the eigenstates,corresponding to a kind of state transformations.[46]Some works based on the electronteleportation,[47]measuring the fermion parity,[48]and encoding the non-local entanglement of MZMs provide an alternative way of detecting the non-Abelian property and constructing the topologically protected quantum gates.[49]Other issues have also been considered, including the state distillation or the error correction.[50,51]However, based on the braiding of the MZMs,it is difficult to realize the T quantum gate,one of the three universal quantum gates.

A recent experiment,inspired by the theoretical proposal of Ref.[60],reported the measurement of the chiral Majorana fermion and observed the half-integer quantized plateau of the Hall conductance.[66]However, alternative theoretical interpretations of the origin of the half-integer quantized plateau led to a skeptical or supportive attitude to the existence of the chiral Majorana fermion.[67–70]Based on the percolation model of QAHI–superconductor–QAHI junction, Huang et al.[67]showed that edge modes could transmit from left to right through the superconducting region with suitable leakage to adjacent chiral edges near the percolation threshold,giving rise to a nearly flat half-integer conductance. Ji and Wen[68]studied the contact conductance under a magnetic field and found that the half-integer conductance is a common result of a good electric contact between the integer quantum Hall insulator and superconductor films. Also, another experiment[71]studied the electric transport of a similar heterostructure of QAHI and s-wave superconductor, and they presented the half-integer quantized conductance without chiral Majorana fermions: two QAHI regions in series with wellaligned magnetization always lead to the half-integer quantized conductance because of the good contact transparency.

Besides the interest in confirming the existence and regulating chiral Majorana fermions, some intuitive ideas turn to braiding chiral Majorana fermions with the purpose of quantum computation. Compared with MZMs, the most exciting property of chiral Majorana fermions is their natural mobility with the potential for rapid information processing.Lian et al.[72]first suggested to perform the braiding of chiral Majorana fermions with a Corbino ring junction. Zhou et al.[73]proposed the braiding-like operation of chiral Majorana fermions via the quantum dot.In addition,Beenakker et al.[74]constructed a device to braid the mobile chiral Majorana vortex around the immobile bulk vortex based on the Josephson junction. Despite these proposals of non-Abelian detections or operations, there is no scheme to implement the universal quantum computation via chiral Majorana fermions,especially the T and CNOT gates.

In this paper,we propose the realization of arbitrary twoqubit quantum gates based on chiral Majorana fermions.Starting from the QAHI–TSC hybrid system, we first construct the elementary cell consisting of a QAHI surrounded by a TSC, which supports two chiral Majorana fermions along the boundary. Then, we introduce an electric gate on the QAHI region and a quantum-dot structure between adjacent cells to braid and partially exchange any two chiral Majorana fermions. Two chiral Majorana fermions in two edge channels within the same cell can be redistributed since the electric gate-induced dynamical phase mixes the electron and hole components. The quantum-dot structure contains two quantum dots, the central one of which allows the quantum tunneling of the chiral Majorana fermions between adjacent cells and the side dot makes up the phase to satisfy the braiding convention. Considering a single qubit defined by four chiral Majorana fermions,the electric gate can tune the trajectory of the chiral Majorana fermions so that half of each incoming chiral Majorana fermion tunnels into the opposite side and the other half keeps its own trajectory,thus realizing an expected T quantum gate. Three braiding operations via two electric gates and one quantum-dot structure achieve an H quantum gate.Based on the minimal definition of two-qubit basis states,we use six chiral Majorana fermions to construct an entangled CNOT quantum gate. Furthermore,the former single-qubit T and H quantum gates are realized within the two-qubit scheme.Besides, we show that a useful quantum Fourier transform algorithm can be decomposed into the aforementioned three quantum gates based on chiral Majorana fermions.

This paper is organized as follows. Section 2 depicts the elementary cell supporting chiral Majorana fermions and explains the function of electric gates and quantum dots to achieve the braiding operation and the partial exchange operation. In Section 3, we construct the quantum gates of the single-qubit and two-qubit gates. In Section 4, a quantum circuit model of the two-qubit quantum Fourier transform is shown with the quantum gates realized via chiral Majorana fermions. We discuss the initialization and measurement of qubits based on chiral Majorana fermions and state the advantage of our proposal in Section 5. We summarize and discuss the further utilization of chiral Majorana fermions in Section 6.

2. Elementary cells for the Braiding and partial exchange operations

That is, the electric gate can regulate the outgoing trajectory of two incoming chiral Majorana fermions.[64]

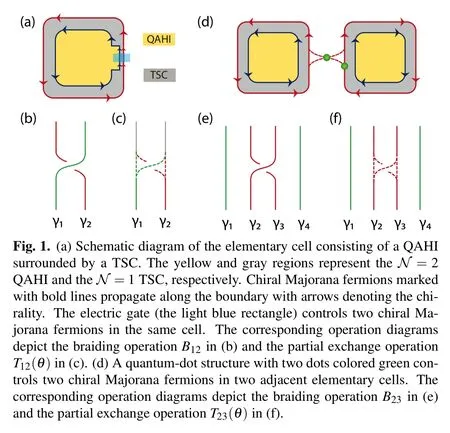
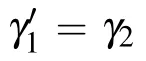
Besides the regulation of two chiral Majorana fermions in the same elementary cell,we introduce the quantum-dot structure to braid and partially exchange chiral Majorana fermions between two adjacent elementary cells. Here the magnetization orientations of two adjacent cells are set in the opposite directions,leading to the chirality of the corresponding chiral Majorana fermions being opposite,as shown in Fig.1(d). As a result,the adjacent chiral Majorana fermions from the adjacent cells have the same mobile direction,which is beneficial for their braiding. A quantum-dot structure of two quantum dots inserts between these two adjacent cells and couples with two adjacent co-propagating chiral Majorana fermions,γ2and γ3. Let us consider the central quantum dot coupling with two chiral Majorana fermions. The Hamiltonian of the chiral Majorana fermions is[73]

Integrate x in Eq.(6)from 0?to 0+,we get

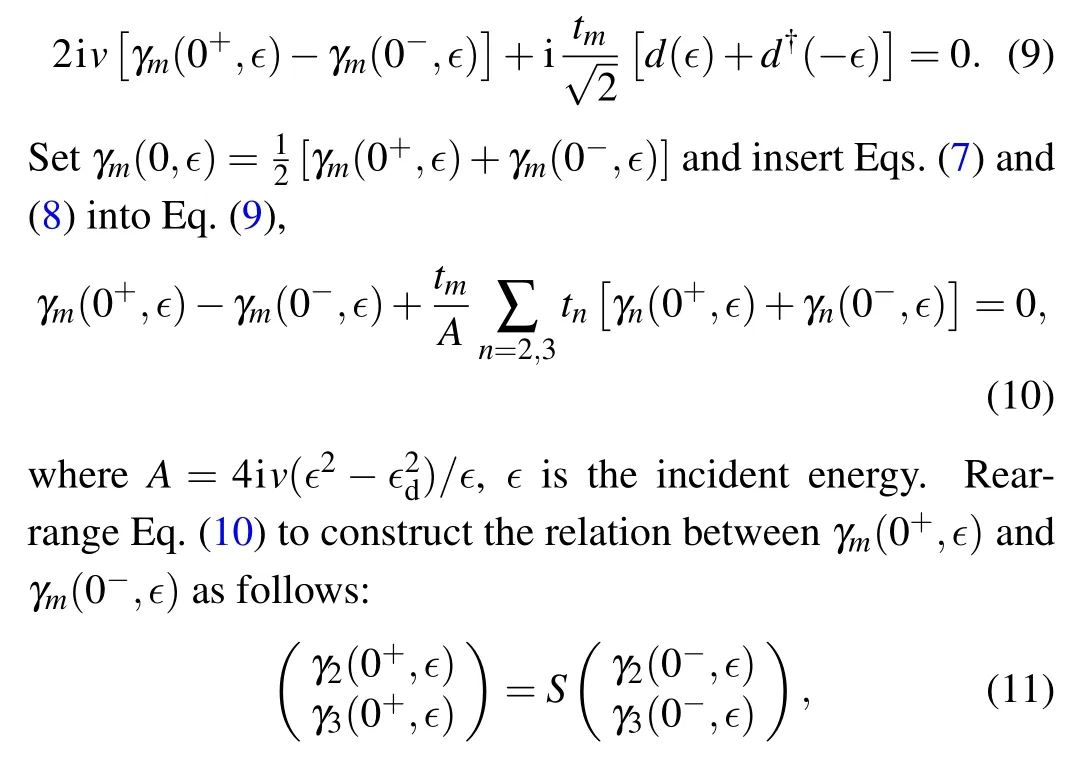
where S denotes the scattering matrix[73]

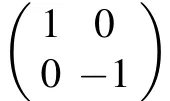
matching the scattering matrix via the electric gate in Eq.(1).When θ =0,the disabled quantum-dot structure has no effect on the chiral Majorana fermions. When θ =π/2,here comes γ2→γ3and γ3→?γ2,that is,the enabled quantum-dot structure completes the braiding operation B23,shown in Fig.1(e).When the relative coupling is tuned to a suitable value, the quantum-dot structure performs the partial exchange operation T23(θ): γ2→cosθγ2+sinθγ3and γ3→?sinθγ2+cosθγ3,as shown in Fig.1(f).

Based on the braiding operation implemented via an electric gate or a quantum-dot structure, we further introduce a transfer box to connect two vertically adjacent elementary cells, as shown in Fig.2(a). Figure 2(b) draws a symbolic picture of a transfer box with four chiral Majorana fermions injecting and ejecting. The transfer box contains two electric gates and two quantum-dot structures arranged in the way shown in Fig.2(c). If the electric gates and quantum dots are disabled, the transfer box is closed, so four chiral Majorana fermions propagate in their own way, (γ1,γ2,γ3,γ4) →(γ1,γ2,γ3,γ4),i.e.,the chiral Majorana pair γ1and γ2remains in the upper cell and the pair γ3and γ4remains in the lower cell. But when the electric gates and quantum dots are tuned to the value corresponding to θ=π/2,the transfer box is open and executes the braiding operations B23,B12,B34,and B23in series.To be specific,four chiral Majorana fermions transform as follows:

Thus, Fig.2(d) clearly shows the function of a transfer box:carry out four braiding operations, exchange of the Majorana pair γ1and γ2with the pair γ3and γ4,and transfer the Majorana pair γ3and γ4from the lower cell to the upper cell. This transfer makes possible cascading vertical cells and braiding chiral Majorana fermions on both sides to be seen in Fig.6.

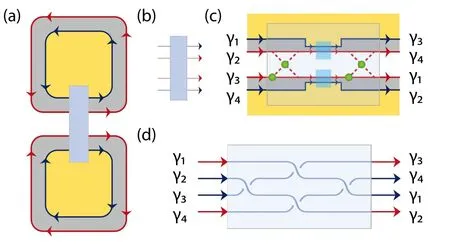
Fig.2. (a) Schematic diagram of two vertically adjacent elementary cells with a transfer box between them. (b)Symbolic picture of the transfer box.(c) The detailed structure of the transfer box with two electric gates and two quantum-dot structures. (d) Braiding diagram of operations B23, B12,B34, and B23, depicting the function of the transfer box as transferring the Majorana pair from the lower cell to the upper cell.

3. Realization of quantum gates

A complete quantum computation process includes three parts:input the qubit,perform the quantum gate operation,and read out the final qubit. The core of quantum computation lies in the realization of arbitrary quantum gates. The standard set of universal quantum gates is{H,T,CNOT},specifically,

Considering the quantum states as qubits, the essence of the quantum gate is the unitary operation in the Hilbert space. In this section,we utilize chiral Majorana fermions as the qubit,use the electric gate and the quantum-dot structure to perform operations on the qubit,and construct the quantum gates in the two-qubit basis to realize any two-qubit quantum operations.

Recalling the elementary cell device in Section 2,we have realized the braiding operation of adjacent chiral Majorana fermions via an electric gate or a quantum-dot structure. Here,we denote the braiding operator of Majorana fermions as[21]

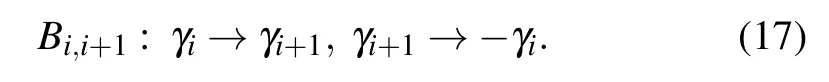
Express the operator in terms of the bilinear Majorana operators as follows:

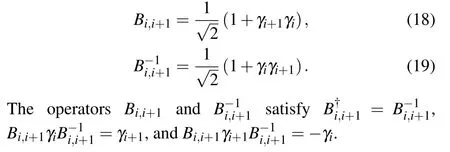
Similarly, for the partial exchange operation, we denote the operator as Ti,i+1(θ),

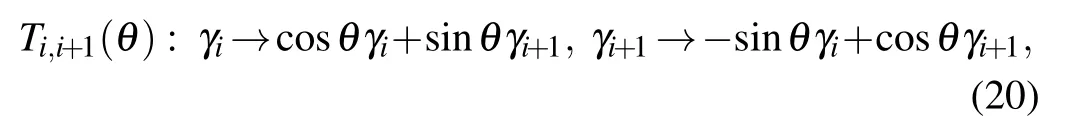
and express Ti,i+1(θ)in terms of the bilinear Majorana operators

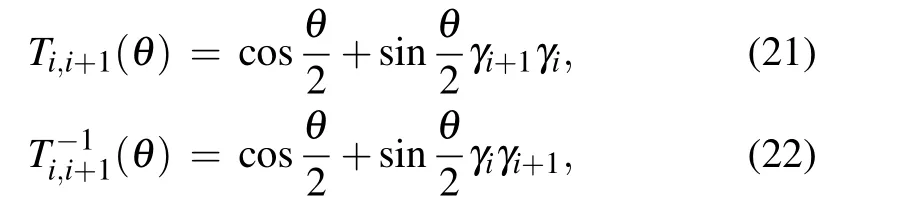
which satisfies

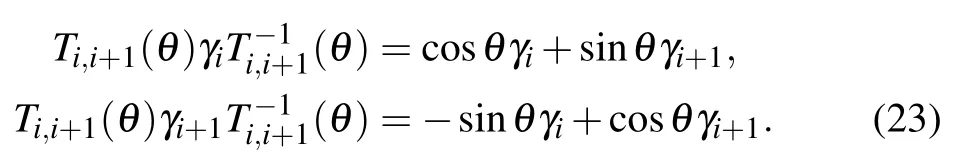
When θ =0, Ti,i+1(0)=1. When θ =π/2, Ti,i+1(π/2)=Bi,i+1,i.e.,the braiding operation represents the total exchange with a dynamical phase being π/2 or equal coupling between the quantum dot and two chiral Majorana fermions.

Hereafter, we regard the braiding operator Bi,i+1and the partial exchange operator Ti,i+1(θ)(θ is not an integer multiple of π/2) as the elementary operations of two chiral Majorana fermions to construct the quantum gates.

3.1. The single-qubit T and H gates

For a single qubit, the minimal number of Majorana fermions is four,due to the fermion parity conservation.[21,76]Thus we place two column of elementary cells to construct the single-qubit quantum device,as shown in Figs.3(a)and 4(a).Four Majorana fermions are input from the lower cells A1 and A2, conveyed via two transfer boxes to the cells B1 and B2,acted on by the quantum operations in the cells B1 and B2,conveyed via two transfer boxes to the cells C1 and C2 as the output. As for the quantum gate,we focus on the core cells B1 and B2 with four incoming chiral Majorana fermions propagating upward,denoted as γ1,γ2,γ3,and γ4from left to right.

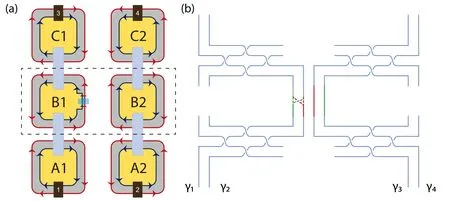
Fig.3. Construction of the T gate. (a) The single qubit device contains two columns of elementary cells supporting four chiral Majorana fermions. The dashed rectangle emphasizes the core region which performs the T gate with an electric gate. (b)Braiding diagram of operations in(a). The dashed cross line represents the partial exchange operation of γ1 and γ2,T1,2(π/4),leading to the transformation of chiral Majorana fermions in Eq.(35).

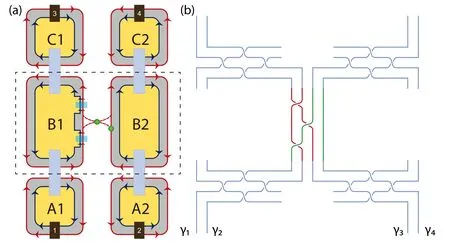
Fig.4. Construction of the H gate. (a) The single qubit device contains two columns of elementary cells supporting four chiral Majorana fermions. The dashed rectangle emphasizes the core region which performs the H gate with two electric gates and one quantum-dot structure.(b)Braiding diagram of operations in(a). The central cross lines represent the braiding operations of B12,B23,and B12 in series,leading to the transformation of chiral Majorana fermions in Eq.(37).

Since Bi,i+1=Ti,i+1(π/2),here comes the matrix form of the braiding operator

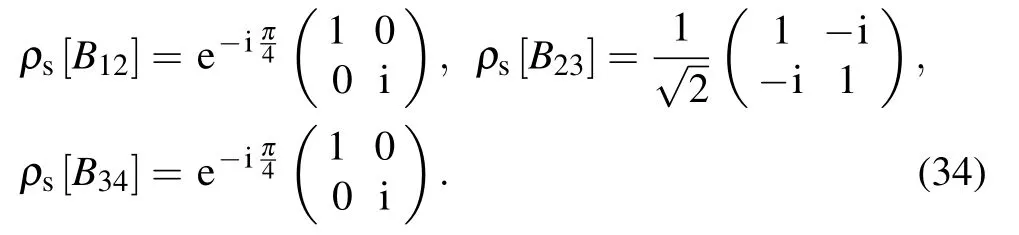
Now we construct the T quantum gate performed on the single qubit composed of four chiral Majorana fermions. The T quantum gate can not be realized by the braiding of MZMs.As shown in Fig.3(a),a gate voltage is applied to the electric gate in the convex QAHI region along the right edge of the elementary cell B1. Tune the gate voltage to achieve the partial exchange operation of chiral Majorana fermions γ1and γ2with θ=π/4,so that one half of the incoming chiral Majorana fermion γ1(γ2) stays in the original path while the other half of γ1(γ2)crosses over and merges into the opposite side[see the dashed crossing curves in Fig.3(b)]. Follow the definition of the operator T12(π/4)in Eq.(20),four chiral Majorana fermions transform as follows:

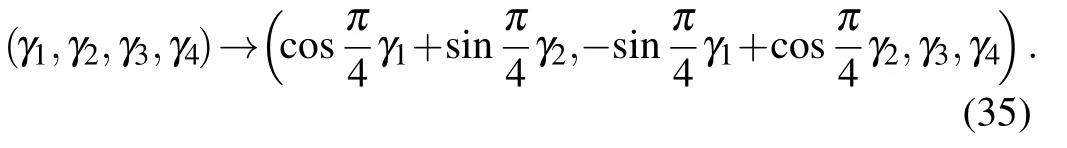
Correspondingly,the single-qubit state basis evolves

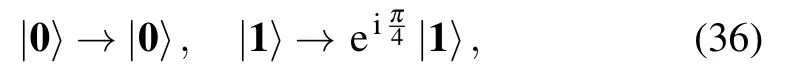
Then we construct the H quantum gate. Via combining the braiding operations in Eq. (34), the H gate could be decomposed into three braiding operations B12, B23, and B12in series, up to an overall phase.[49,78]We introduce two electric gates to braid chiral Majorana fermions within the elementary cell B1 and one quantum-dot structure to braid between cells B1 and B2,as shown in Fig.4(a),that is,

Correpondingly,the single-qubit state basis evolves

which is indeed the unitary transformation under the H gate with the definition in Eq.(16).

3.2. The two-qubit CNOT gate

where the central qubit labeled by M serves as the ancillary qubit to balance the fermion parity.

where I2is a 2-by-2 identity matrix. These four matrices are not entangled since they can be decomposed into the direct product of single-qubit matrices.[1]However, considering the braiding operator of γ3and γ4, the matrix form is derived as follows:Noticeably,the braiding operator B34is an entangled operator since the matrix ρt[B34] cannot be decomposed in the direct product form.

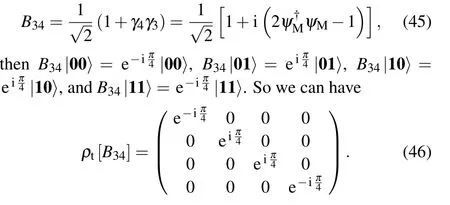
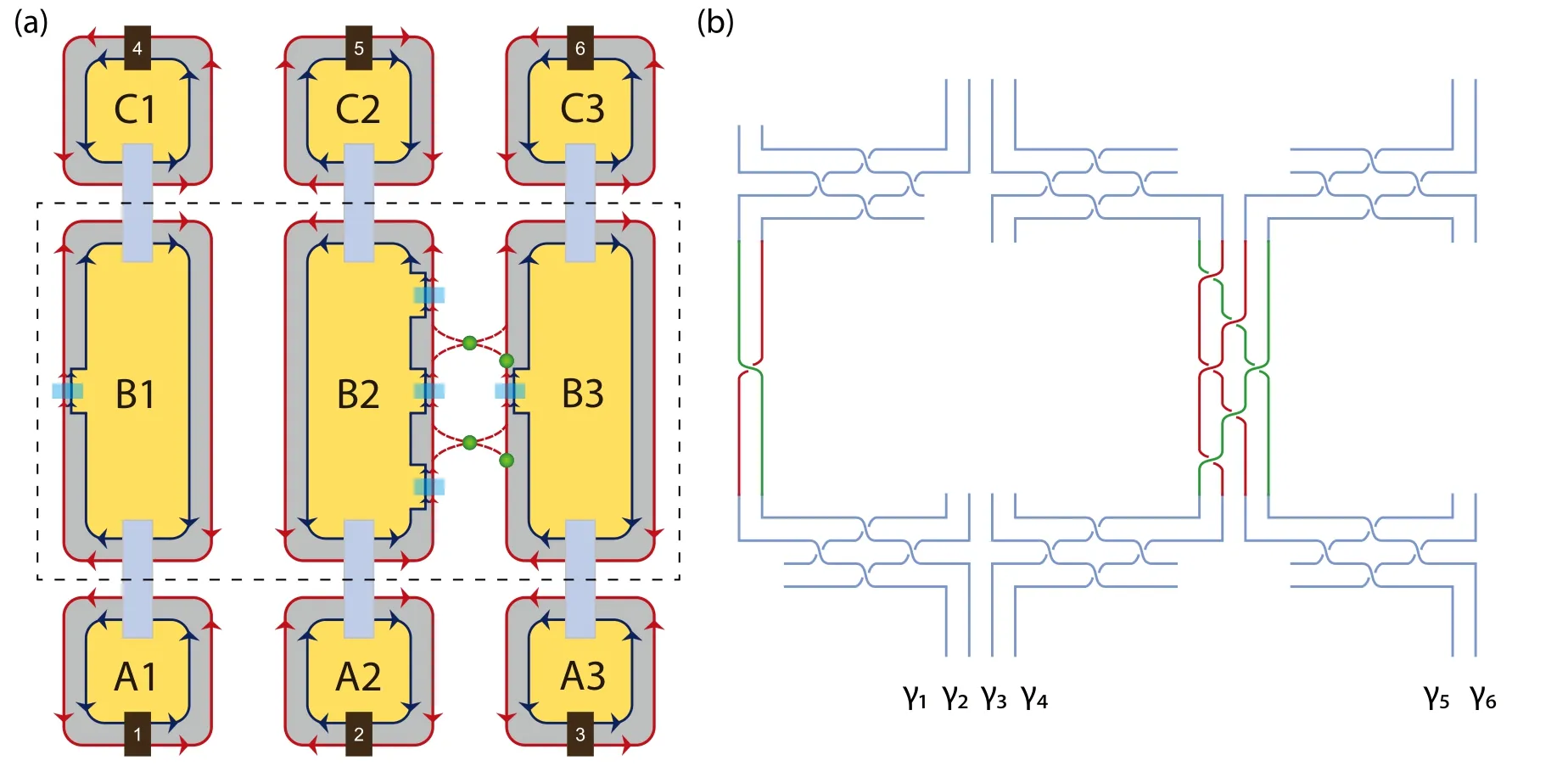
Fig.5. Construction of the CNOT gate. (a)The two-qubit device contains three columns of elementary cells supporting six chiral Majorana fermions. The dashed rectangle emphasizes the core region which performs the CNOT gate with five electric gates and two quantum-dot structures. (b)Braiding diagram of operations in(a). The central cross lines represent the braiding operations of B34,B45,B56,,B34,B45,B34 in series, leading to the transformation of chiral Majorana fermions in Eq. (48). Note here the is the inverse braiding of γ1 and γ2,realized by an opposite value of the gate voltage corresponding to B12.

The entangled operator is vital in the quantum computation since it introduces the entanglement into the quantum state.One of the famous entangled quantum gates is the CNOT gate(the controlled-NOT gate)performing a conditional operation on the two-qubit state [see the matrix form of CNOT gate in Eq. (16)]. After a CNOT gate, the control qubit remains while the target qubit transforms according to the state of the control qubit: if the control qubit is 1, the target qubit reverses its state;if the control qubit is 0,the target qubit keeps its state.

Combining the basic braiding operators in two-qubit basis,the CNOT gate is decomposed into seven braiding operations up to an overall phase as follows:[76]

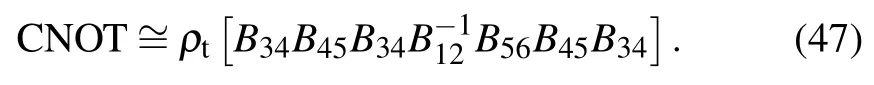
We construct a device to realize the CNOT gate via five electric gates and two quantum-dot structures, as shown in Fig.5(a). The effect of seven braiding operations from Eq. (47) in series on the six chiral Majorana fermions of cells B1,B2,and B3 is

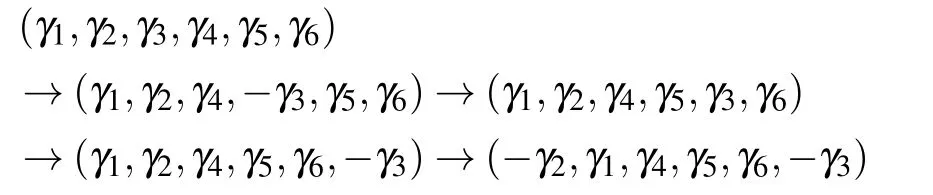
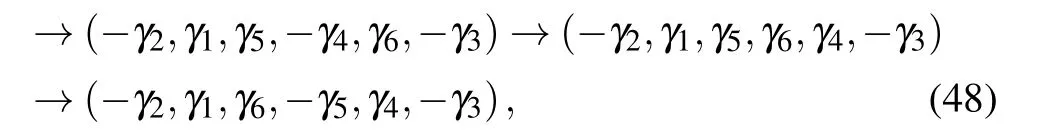
3.3. The T and H gates in the two-qubit basis

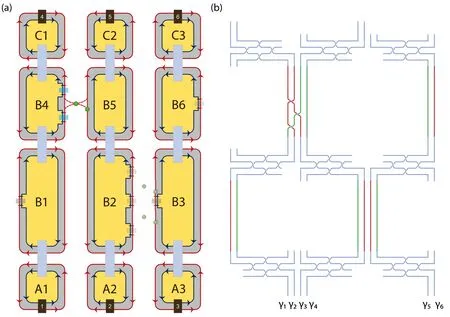
Fig.6. H gate acting on the left qubit in the two-qubit basis. (a)The two-qubit device contains three columns of elementary cells supporting six chiral Majorana fermions. The colorful electric gates and quantum dots are enabled while the gray ones are disabled. The H gate acting on the left qubit is realized when opening electric gates and quantum dots of cells B4 and B5. Besides,other single-qubit gates or CNOT gate can be realized when enabling other cells in the same was as core regions in Figs.3–5. (b)Braiding diagram of operations in(a). The central cross lines represent the braiding operations of B12,B23 and B12 in series,leading to the same transformation of chiral Majorana fermions in Eq.(37).

To realize the H gate on the left qubit HL, we construct the device as shown in Fig.6(a). Two cells, B4 and B5,are crucial to perform the HLgate. Two electric gates and one quantum-dot structure achieve the braiding operations B12, B23, and B12. Multiplying the matrices of these operators in Eq.(43)gives the HLgate up to an overall phase,

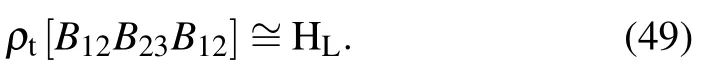
Correspondingly,Fig.6(b)depicts the braiding of γ1and γ2,γ2and γ3,γ1and γ2in series.

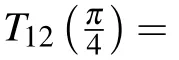
Based on quantum gates HL, HR, TL, and TR, all nonentangled single-qubit gates could be achieved. Easily to see,the CNOT gate is compatible with the device in Fig.6(a).Combined with HL, HR, TL, TR, and CNOT, arbitrary twoqubit gate can be constructed. Thus, the device plotted in Fig.6(a)can perform arbitrary two-qubit quantum gate based on six chiral Majorana fermions.

4. The quantum circuit of the quantum Fourier transform

After the realization of quantum gates T, H, and CNOT,as an example,we state that the algorithm of quantum Fourier transform (QFT) can be realized via the two-qubit device of chiral Majorana fermions shown in Fig.6(a).

As for the realization of quantum gates in the QFT circuit, the single-qubit H gate acting on either qubit has been discussed in Subsection 3.3. The two-qubit CS gate can be decomposed as CS=CNOT·(I ?T?1)·CNOT·(T?T)[see the equivalent circuit in Fig.7(b)].[1]Similarly,the T?1can be realized by inversing the sign of the gate voltage corresponding to the T quantum gate.

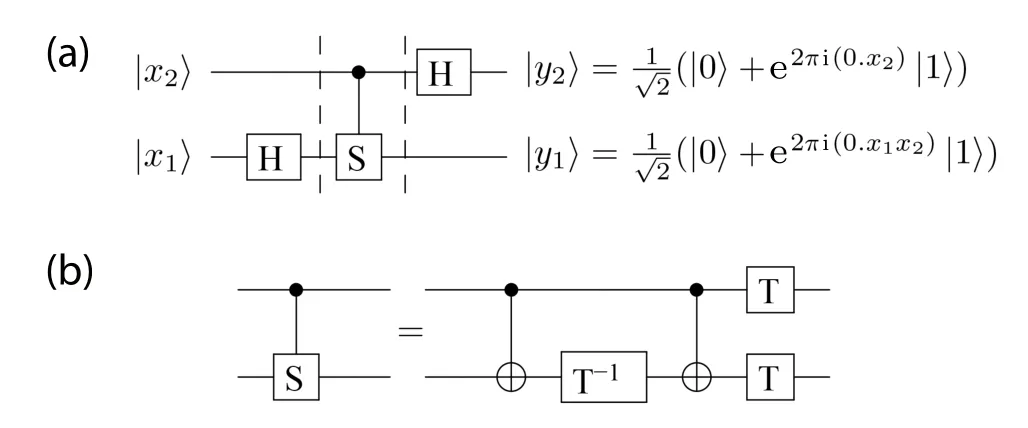
Fig.7. (a)A two-qubit quantum circuit realizes the quantum Fourier transform. (b) The controlled-S gate is decomposed into the quantum gates CNOT and T. T?1 denotes the inverse of T gate, realizable by an opposite gate voltage of T gate.

5. Discussion on initialization and readout of qubits

Besides the quantum gates proposed above to realize quantum operations on qubits,here we briefly discuss the initialization and measurement of qubits based on chiral Majorana fermions.

Considering the conventional physical qubits, information is encoded in the degree of freedom such as photons,spin,or the electric charge. For the photon qubit,[3,6]the initialization is to create single photon states by attenuating laser light and drive them into certain polarization through optical polarizers and the measurement is to detect single photons,e.g.,by a photomultipler tube.For qubits realized by nuclear magnetic resonance,[79]the initial state is prepared in a strong magnetic field to polarize the spins and the readout process is to measure the voltage signal induced by precessing magnetic moment.As to the charge qubit based on the superconducting Josephson junctions[15]or the singly charged quantum dot pair,[10]the electron number is used as the basis state of qubit. These charge qubits can be initialized by electron injection via a current pulse or voltage pulse and the electronic charge state is straightforward to be measured by the quantum point contact or another quantum dots due to their high sensitivity to the conductance response to the applied gate voltage.[12,80,81]

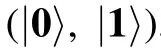
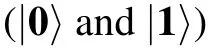
Here it is worth mentioning that the partial exchange operation of the chiral Majorana fermions via these electric gates is not topologically protected. But it can be well controlled within the time scale ps, presenting the faster speed of information processing than physically moving or measuring Majorana zero modes. Except the gate operating region,the propagation of chiral Majorana fermions is topologically protected with no backscattering and no additional complex phase. Thus, our proposal owns the advantage of quantum computations based on chiral Majorana fermions: the fast speed of quantum computation well preserves and it partially displays the topological protection.

6. Conclusion

We have constructed the realization of arbitrary two-qubit quantum gates based on chiral Majorana fermions. The elementary cell which consists of a quantum anomalous Hall insulator surrounded by a topological superconductor with some electric gates and quantum-dot structures realizes the braiding operation and the partial exchange operation. Single-qubit operations,T and H quantum gates,are completed via one partial exchange and three braiding operations among four chiral Majorana fermions.An entangled two-qubit gate,the CNOT gate,is achieved via braiding six chiral Majorana fermions.We also show a design which can perform several quantum gate operations in series. These two-qubit quantum gates are used to the quantum circuit model of a simple quantum Fourier transform. This proposed device could be used for more interesting algorithm.