Growth mechanism and characteristics of electron drift instability in Hall thruster with different propellant types
Long Chen(陳龍), Zi-Chen Kan(闞子晨), Wei-Fu Gao(高維富), Ping Duan(段萍),Jun-Yu Chen(陳俊宇), Cong-Qi Tan(檀聰琦), and Zuo-Jun Cui(崔作君)
School of Science,Dalian Maritime University,Dalian 116026,China
Keywords: Hall thruster,electron drift instability,axial electron mobility,particle-in-cell simulation
1.Introduction
The Hall thruster is a well-developed annular electromagnetic propulsion device that is widely used because it meets the needs of space propulsion missions such as attitude control,orbit transfer, and inclination correction of space vehicles.[1–3]The Hall thruster forms a radially distributed magnetic field through coils arranged outside the inner wall and outer wall of the discharge channel, and the potential drop between the anode and cathode forms an axially distributed electric field.Under the orthogonal electromagnetic field,the electrons emitted from the cathode perform Hall drift motion along the azimuthal direction of the channel and collide with the propellant gas atoms injected into the channel from the anode to produce plasmas.The ions are then accelerated by the axial electric field to generate thrust.Since the ion mass is significantly greater than the electron mass and the ion Larmor radius exceeds the size of the discharge channel, ions are commonly regarded as non-magnetized.The electrons experience an azimuthal drift velocity on the order of 106m/s due to the action of the orthogonal electromagnetic field.This velocity difference between the electrons and ions in the azimuthal direction induces a significant plasma instability in the discharge channel,which is known as electron drift instability(EDI).Tsikataet al.[4]measured the oscillation of electron density in the discharge channel of a Hall thruster using a collective light scattering method.The experiment indicated that EDI exhibits high-frequency oscillation in the order of~MHz in both the azimuthal direction and radial directions.
The evolution of high-frequency short-wave oscillations of EDI can be effectively observed by particle-in-cell (PIC)simulations.The majority of studies have used PIC simulation that contains azimuthal direction to simulate these oscillations.These models include one-dimensional (1D) azimuthal direction,[5–7]two-dimensional (2D) axial-azimuthal directions,[8–12]2D radial-azimuthal directions,[13–16]and three-dimensional (3D) full-channel[17,18]numerical simulations.Ducrocqet al.[19]investigated the development of EDI and suggested that when the electric drift velocity is smaller than the electron thermal velocity,the EDI fluctuations satisfy an ion-sound wave dispersion relation and the saturation of the EDI may be related to ion Landau damping.Laflueret al.[7,20]proposed the corresponding dispersion relation for EDI by establishing a 1D azimuthal direction PIC simulation.The study by Coche and Garrigues[21]found that reducing plasma density can effectively suppress EDI.Taccognaet al.[9]studied the development process of EDI by building two different 2D models of the channel and showed that EDI triggers off both radial and azimuthal plasma oscillations and that the nonlinear development in the phase exhibits ion-acoustic wave properties.Senguptaet al.[13]studied the nonlinear growth phase of EDI by full-scale 2D simulation in the radial direction and azimuthal direction.They showed that the wavelength of EDI increases with nonlinear growth phase and that the saturation of EDI is strongly correlated with the motion of the ions in the azimuthal direction.It is clear that EDI shows different characteristics in each growth stage due to different excitation mechanisms.Tavassoliet al.[22]showed that in numerical simulation studies of EDI,numerical noise often significantly affects the simulation results and obscures the actual growth mechanisms at each stage.Asadiet al.[23]showed that increasing the number of macro-particles in the model can eliminate the numerical noise to some extent.
The EDI is considered to be one of the main reasons for anomalous axial electron transport.[24–30]Lazurenkoet al.[31]demonstrated experimentally that the EDI significantly increases the axial electron mobility of the thruster.Laflueret al.[5]established a modified model of the electron axial mobility under the influence of EDI through theoretical derivation,and the modified electron mobility is in the same order of magnitude as the actual value.Lafleur and Chabert[11]developed a 2D model in the axial-azimuthal direction and demonstrated that anomalous electron transport can be explained by an instability-enhanced friction force between electrons and ions.
Xenon gas is widely chosen as the propellant in traditional Hall thrusters, owing to its low ionization energy and chemical stability.In recent years,other types of propellants,such as argon and krypton, have also been proposed as propellants for Hall thrusters to reduce costs.[32,32–35]The EDI is expected to exhibit different characteristics under different types of propellants,thereby affecting the discharge process of Hall thrusters.Asadiet al.[23]investigated the axial electron mobility variation under the effect of EDI for different propellants corresponding to ion weight.However, the study used the same collision cross-section, which may not fully reflect the true influences of different propellants on EDI characteristics.
From the content mentioned above, it can be observed that the precise growth mechanisms of EDI at different stages(linear and nonlinear) remain undetermined, and the detailed characteristics of EDI in Hall thrusters with different propellant types have not been comprehensively studied.Additionally, the effects of electromagnetic field strength and propellant types on the axial electron transport caused by EDI have not been thoroughly investigated.Based on the typical size and operating parameters of the Hall thruster, a 1D physical model of the azimuthal discharge channel is established in this work.In this model, the number of particles is increased to reduce the influence of numerical noise on the simulation results, and the actual differential scattering cross-sections for different types of propellants are considered.The improved 1D azimuthal PIC model is employed to investigate the development process of EDI and the influences of different propellants on EDI and electron axial migration rate.
The rest of the paper is organized as follows.The physical model is established and the basic equations are introduced in Section 2.In Section 3,the numerical simulation results are described and analyzed.Finally,the results are summarized in Section 4.
2.Physical model and basic equations
The discharge channel of the thruster is an annular space formed by an inner ceramic sleeve and outer ceramic sleeve.The wavelength of the EDI is within the millimeter range,which is significantly smaller than the dimension of the Hall thruster discharge channel.Hence, the influence of curvature in the azimuthal direction in this model is not considered.Figure 1 shows a typical 3D structure of the Hall thruster and a schematic of the simulation region for this study.The thruster discharge channel is expanded in the azimuthal direction,and the profile is taken in the channel axial direction to establish a 2D coordinate phase space and a 3D velocity phase space.The lengths of the axial boundary and azimuthal boundary of the respective discharge channels in the simulation area are represented byLzandLyrespectively.A radial magnetic fieldB0perpendicular to the axial-azimuthal plane is applied to the simulation area,and a uniform and constant axial electric fieldE0is applied in thezdirection.The electric field strength in the simulation area is set to 2×104V/m, and the magnetic field strength is assumed to be 200 Gs(1 Gs=10?4T).[37]
The particle positions are tracked in the axial direction and azimuthal direction,and the axial electric field component is provided by the applied electric fieldE0,while the azimuthal electric field component is obtained by solving Poisson’s equation in the azimuthal direction.It is worth noting that the 1D model established in this study solves the Poisson equation only in the azimuthal direction.The particles in this simulation exist in a 2D positional coordinate space and a 3D velocity space.
The electrons are magnetized and their collisions with xenon atoms are considered in the simulation,including single ionization, excitation, and elastic scattering reactions, which are processed by the Monte Carlo collision(MCC)algorithm.Only energy loss and scattering are considered in the treatment of ionization and excitation collisions,and neither newly generated electrons nor ions are added to the simulation area.Additionally,because of the significant difference in mass between ions and electrons,this model does not take into account the influence of the magnetic field on ions.The influence of the axial electric field on ion motion is limited to changing the effective transit time through the acceleration region.Due to the smaller axial length of the simulation region than the actual size of the Hall thruster discharge channel, the ions are given an additional constant axial velocity,vdito simulate the ion motion near the exit of the discharge channel.
The boundary conditions of the simulation region are set as follows.The azimuthal angular boundary uses periodic boundary conditions, while the axial boundary uses the following conditions: ions passing through the exit plane of the axial region are removed from the simulation and replaced by new ions loaded at the entrance with an initial temperature of 0.1 eV; electrons lost at the entrance plane are removed and replaced by new electrons loaded at the exit plane with an initial temperature of 10 eV.The parameters are selected from the literature.[23,37,38]Consequently,the total number of“macro particles”and the overall plasma density are kept constant.When new particles are loaded, their azimuthal positions are randomly distributed within the range ofLy.Table 1 displays the parameters of the physical quantities used in the simulation region.The values of the magnetic field intensity and the electric field intensity are chosen based on the parameters near the exit of a classical Hall thruster discharge channel.[1,34,36,39]Simultaneously, considering program runtime, computational load, and the actual values within Hall thruster discharge channels,[36]in the model a simulation region is specified to have an axial length of 1 cm and an azimuthal length of 2.75 cm.
In the model a fixed time step is set to 5×10?12s,and a fixed grid cell length to 5×10?5m.These set values ensure that the model continues to satisfy the Courant–Friedrichs–Lewy (CFL) condition even after electron temperature has rised.[40]
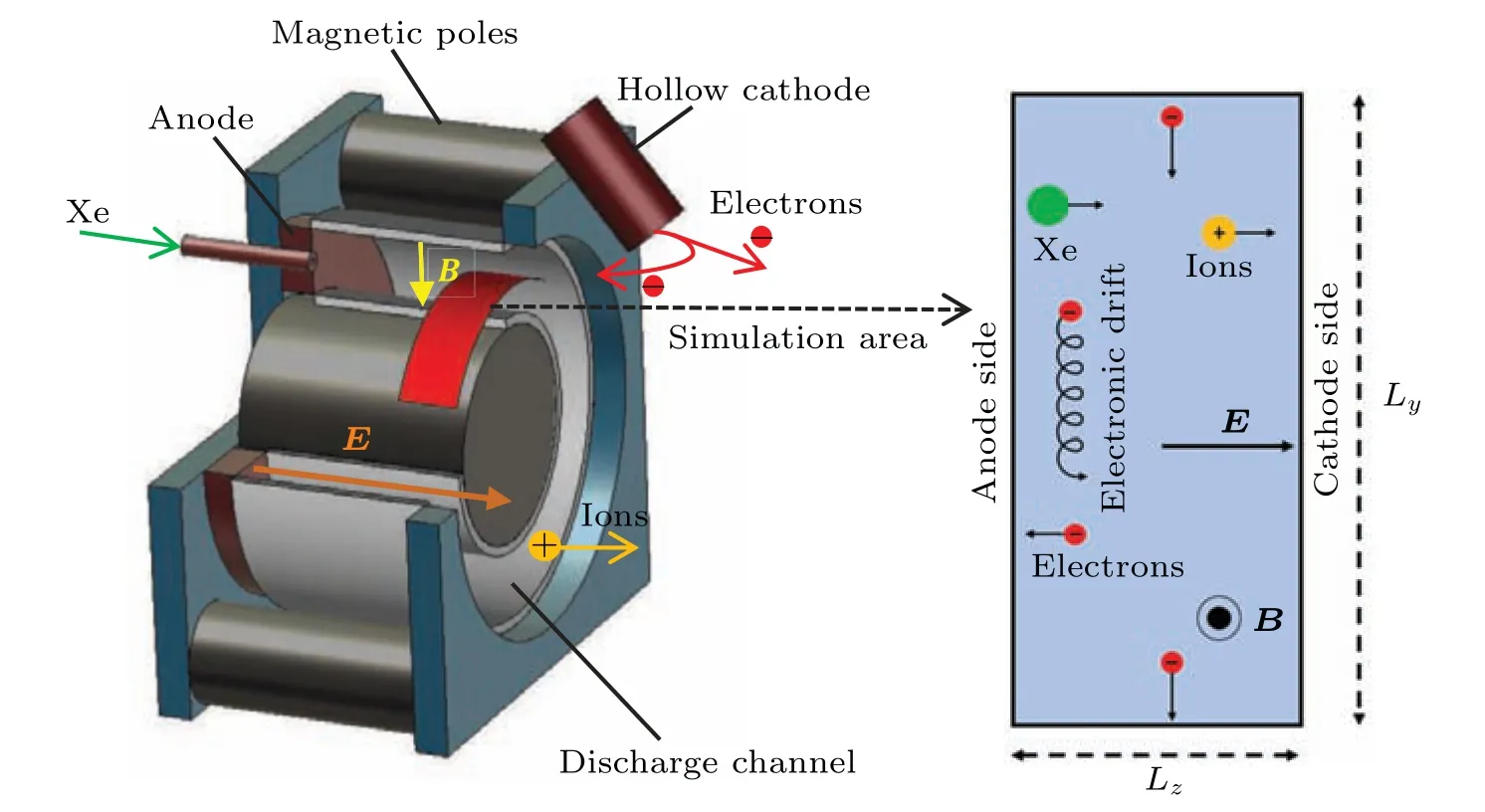
Fig.1.Typical 3D structure of Hall thruster and schematic diagram of simulation region.
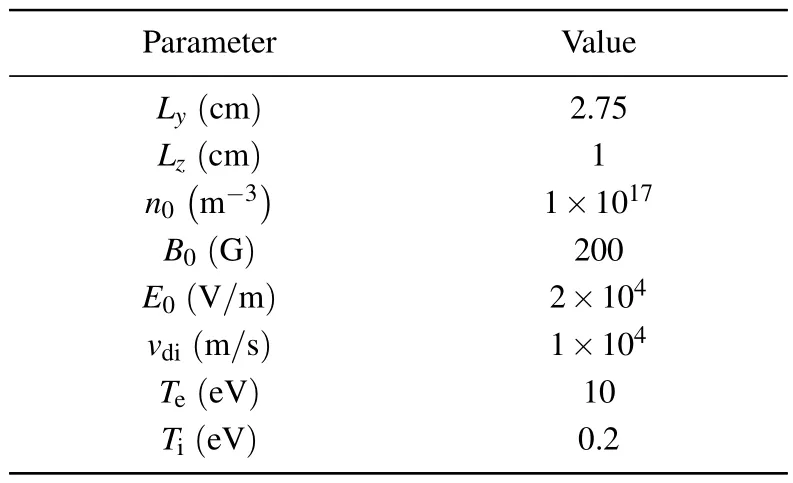
Table 1.Physical parameters used in PIC simulation.
Furthermore, to minimize the influence of numerical noise on the simulation results, the model increases the total number of“macro particles”compared with the conventional 1D model.Specifically,1000 particles are allocated to per cell.Table 2 displays the variations in oscillation frequency, particle energy,runtime duration,and coefficient of determination(R2)in the EDI’s quasi-steady phase with different numbers of particles per cell(Nppc)in the simulation program.Here,R2is calculated from the approximate fitting to the electron density oscillations at 6μs by using the sum of sin functions curve:
whereyirepresents the actual value being fitted, ?yirefers to the fitted value, and ˉydenotes the mean of the actual values.The coefficient of determinationR2measures the quality of the fitting of the fitted values to the true values.When fitting electron density oscillates,R2can also reflect the smoothness of the oscillation curve of electron density.A smoother curve indicates less numerical noise in the program.
From Table 2, it can be observed that whenNppc≤500,the oscillation frequency of EDI, and particle energy show noticeable and irregular variations due to the value ofNppcchanging.However,whenNppc>500,all parameters listed in Table 2 exhibit insignificant differences when particle counts change.It can also be seen from Table 2 that with the increase ofNppc, theR-squared value after fitting the electron density oscillations also increases.This implies that withNppc>500,it is sufficient to reduce the interference of numerical noise to the results of simulation program.Considering the program runtime,the program is set withNppc=1000.

Table 2.Frequencies,particle energy,coefficients of determination,and runtimes in EDI’s quasi-steady phase with different numbers of particles per cell.
3.Simulation results and discussion
3.1.Driving force and development process of EDI
The main features of EDI are high frequency reaching to~MHz,large-amplitude oscillations of the azimuthal electric field and the plasma density in the channel.The simulation uses a time step of 2.5×10?10s and observes oscillation in the azimuthal electric field and electron density at a frequency of 5 MHz.Figures 2(a) and 2(b) show the temporal evolution of azimuthal electric field and electron density, revealing that the electron density oscillation lags behind azimuthal electric field oscillation, which means that the plasma density oscillation is triggered off by the electric field.As EDI develops, the maximum amplitude of azimuthal electric field oscillation can reach to 8 times the magnitude of the applied axial electric field, while the electron density oscillation can reach to 2 times the plasma density.Figure 2(c) shows the oscillation of azimuthal electric field in the first 0.375μs.Figure 2(d)shows the temporal evolution of the amplitude of azimuthal electric field oscillation in 0–3 μs.Comparison of Fig.2(c) with Fig.2(d) shows that the oscillation of the azimuthal electric field initiates at 0.1 μs, and EDI undergoes a linear growth phase for the first 0.375 μs.The amplitude growth of azimuthal electric field oscillation exhibits an exponential growth characteristic during the linear growth period.Theγin Fig.2(d)shows the amplitude linear growth rate normalized by the ion plasma frequency.The azimuthal electric field distribution at each time point is subjected to a fast Fourier transform (FFT), and the amplitude corresponding to the maximum frequency is selected as the characteristic amplitude at the corresponding time, followed by a linear fit to calculate the amplitude growth rate.
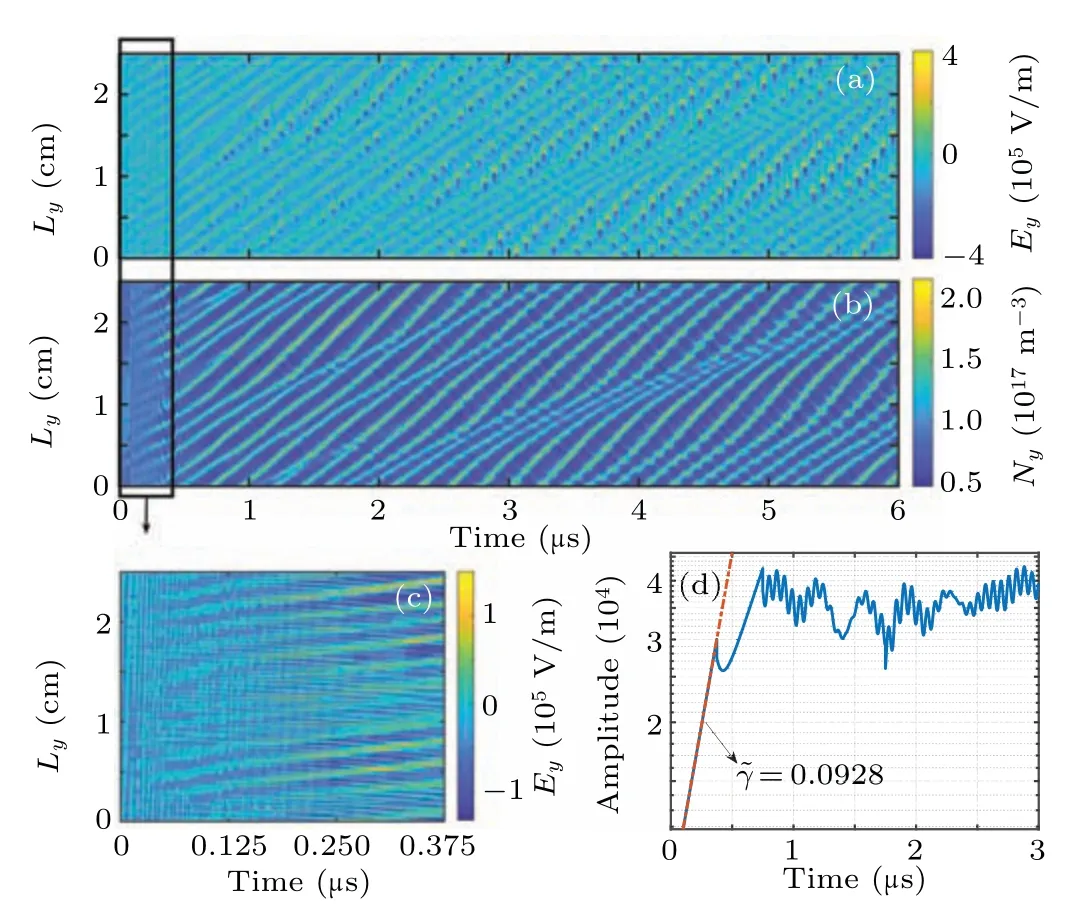
Fig.2.Temporal evolution of azimuthal electric field, electron density, and the temporal evolution of the amplitude of azimuthal electric field oscillations: (a) electric field in azimuthal direction, (b) electron density, (c) azimuthal electric field evolution during the linear growth phase,(d)amplitude of the azimuthal electric field.
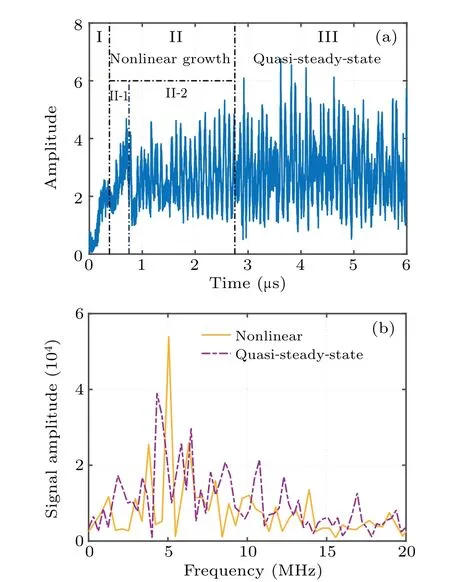
Fig.3.Temporal evolution of amplitude of azimuthal electric field oscillations and the corresponding frequency spectrum analysis: (a) amplitude evolution(I:linear growth phase;II:nonlinear growth phase;III:quasi-steady-state phase), (b) frequency spectrum at nonlinear growth and quasi-steady-state stages.
Figure 3 shows the temporal evolution of the amplitude of azimuthal electric field oscillation and the corresponding frequency spectrum analysis, here, the amplitude is normalized by the axial electric field strength.As shown in Fig.3(a),the amplitude variation of EDI follows a linear growth relationship before 0.375 μs.At the timepoint of 0.375 μs,where the amplitude reaches 2.5 times the axial electric field,the linear growth relationship is disrupted, and the growth rate slows down.At the timepoint of 0.75 μs, the amplitude of the EDI experiences a sharp drop, followed by oscillation and slow growth.After the 2.75 μs, EDI enters a high-amplitude oscillation mode,with the amplitude reaching to 7 times the strength of the axial electric field.Three clear evolution phases are shown in this process of EDI: (I) linear growth phase (0.1 μs–0.375 μs), in which the amplitude of the azimuthal electric field oscillation increases linearly; (II)nonlinear growth phase (0.375 μs–2.75 μs): EDI enters the first nonlinear growth phase(II-1 shown in Fig.3(a)),in which the amplitude of EDI continues to increase, but no longer follows the linear growth rate; after 0.75 μs, EDI enters the second phase of nonlinear growth (II-2 shown in Fig.3(a)),where the oscillation amplitude of EDI increases slowly and exhibits pronounced oscillation;(III)quasi-steady-state phase(after 2.75 μs): EDI reaches saturation finally, where the oscillation frequency no longer changes and the amplitude exhibits irregular oscillation.The spectrum analysis of the nonlinear growth phase and quasi-steady-state period of the EDI are shown in Fig.3(b).As can be seen from this figure, the EDI has a major frequency of 5 MHz in the nonlinear growth phase,and the major frequency of EDI decreases to 4.9 MHz after entering the quasi-steady state.
Figure 4 shows the temporal evolution of the average particle energy and its azimuthal energy within the simulation region.As shown in Fig.4(a),the average energy of ions rapidly increases, and reaching 95 eV at the 0.75μs.This is primarily due to the acceleration of ions in the axial direction by the applied electric field.Subsequently, the ion energy undergoes oscillation until the EDI reaches a quasi-steady state.The electron energy first increases briefly,then decreases,and eventually stabilizes with oscillations in a range from 30 eV to 45 eV.From Fig.4(b),it can be observed that the azimuthal ion energy starts to increase from 0.1 eV after the onset of EDI.It exhibits different growth patterns during different stages of EDI development until it stabilizes at 6 eV after the EDI enters a quasi-steady state.The variation of electron temperature in the azimuthal direction follows a similar trend to the overall energy change.This means that due to EDI,there occurs a significant ion heating mechanism in the azimuthal direction.It is worth noticing that the variation of azimuthal ion energy during the linear growth and the first nonlinear growth phase of EDI shows a similar trend to the amplitude variation shown in Fig.3(a),which exhibits a short and rapid initial increase, followed by a brief decrease and then a slow growth.These pieces of evidence indicate a close relationship between the azimuthal ion heating mechanism and the evolution of EDI.To investigate the ion heating mechanisms of EDI and their relationship with the development of instability,four time points,denoted ast1=0.1μs,t2=0.375μs,t3=0.75μs,andt4=2.75μs,to represent different stages of EDI development,are selected.The azimuthal particle density oscillations,velocity phase space evolution,and changes in velocity distribution fitting profiles at each of these time points are shown in Figs.5–7.
Figure 5 shows the azimuthal distributions of electron density and ion density at different time points.It can be observed that the electron density distribution oscillates before the ion density distribution.As the particle energy increases,the amplitude of plasma density oscillation also increases.Att2=0.375 μs, the amplitude of the plasma density reaches twice that of the initial density and stabilizes.This is because electrons have a higher azimuthal velocity than ions.Because of this velocity difference, the electron density oscillates before the ion density, and the oscillation of ion density is triggered off through their interactions.The interaction between electrons and ions, which results in oscillation in ion density and energy loss for electrons in the azimuthal direction, is commonly referred to as electron–ion friction.By combining Figs.4(b) and 5, it can be observed that EDI induces a deceleration of electrons and an acceleration of ions through the increase of electron–ion friction in the azimuthal direction.When electron density oscillation and ion density oscillation are almost synchroinous,the ion azimuthal energy reaches its maximum value of 6 eV, and the amplitude of ion density is slightly higher than that of electron density.
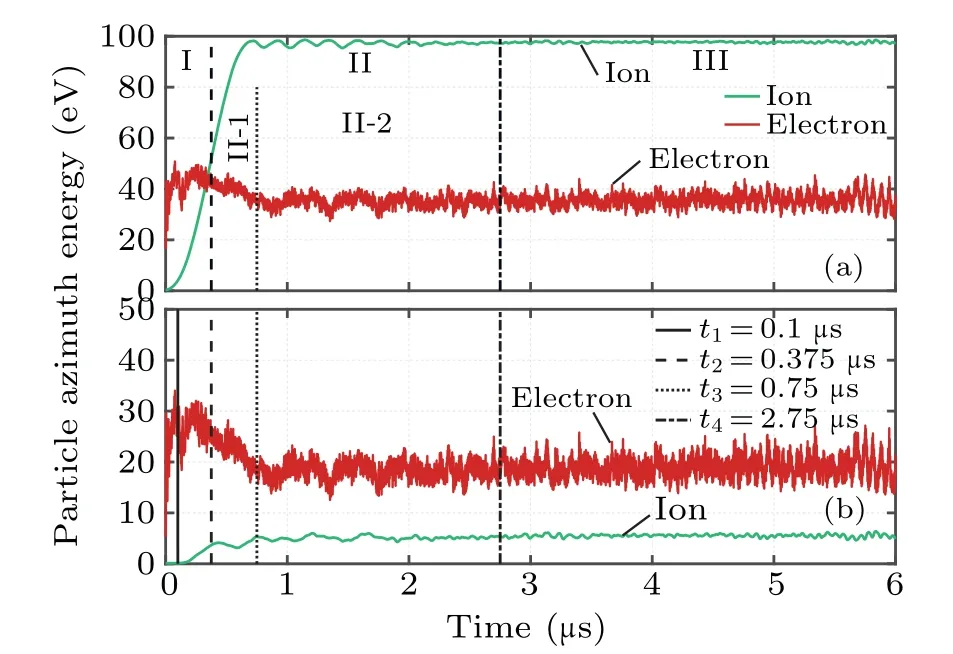
Fig.4.Temporal evolution of (a) average particle energy and (b) its azimuthal energy in simulation region.
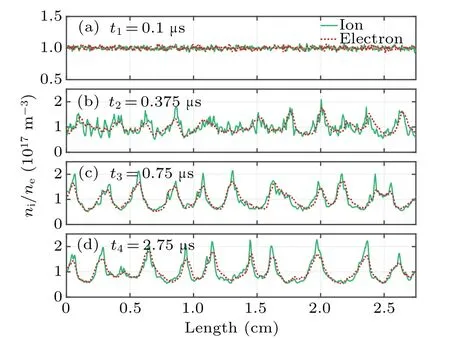
Fig.5.Ion density distributions and electron density distributions at different time points.
Figure 6 shows the evolutions of the ion phase space plot in azimuthal direction at different time points.As observed in this figure,the ion phase space gradually forms a vortex structure.Att3=0.75μs,vortices start to emerge in the ion phase space, accompanied by the formation of a striped long-tail,while the amplitude of the instability oscillation increases to a larger amplitude.Att4=2.75 μs, the majority of ion velocities are limited within the range of±5000 m/s.Combining with Fig.3(a), it can be observed that EDI exhibits irregular amplitude oscillations att3=0.75μs.This is due to the fact that aftert3=0.75μs, the EDI wave of the phase velocity is close to the ion thermal velocity.Under the influence of nonlinear Landau damping, the EDI and ions are interacted with each other, entering the nonlinear development phase.After entering the nonlinear phase, resonance occurs between the EDI wave and ions with velocities close to the wave speed.When there is a larger number of ions with velocities lower than the wave velocity, the particles gain more energy from the wave than their contribution to it.This explains the difference in the growth trend of ion azimuthal energy between the nonlinear growth stage and the linear growth stage in Fig.4(b).This phenomenon hinders the development of EDI and further heats the ions in the azimuthal direction.This is consistent with the phenomenon observed in the experiment in Ref.[41].As the ion velocity increases,distinct vortex patterns appear in the ion phase space,indicating that the ions are trapped in potential wells.Starting from this stage,the trapped ions exhibit energy oscillation as shown in Fig.4(a).
Figure 7 shows the fitted azimuthal ion velocity distribution profiles at different time points.The dotted lines in Fig.7 represent Maxwellian distributions of the velocity distribution function (VDF) for ions with the same temperature at the corresponding time.The dotted dash lines indicate the wave speed of EDI at the corresponding time points.From Fig.7, it can be observed that the ion azimuthal velocity follows the Maxwellian distribution when EDI starts to generate.However, as EDI grows, the ion azimuthal velocity gradually deviates from the Maxwellian distribution.The actual velocity distribution profile is broader than the Maxwellian distribution,with the proportion of high-speed ions increasing significantly.This broadening effect is attributed to ion acceleration in the azimuthal direction, caused by electron–ion friction which results in the ions velocity deviating from the typical Maxwellian distribution.As shown in Figs.7(b)–7(d),the velocity distribution profiles in the azimuthal direction gradually shift towards positive values with ion energy increasing.Moreover, the portion of the velocity distribution profile exceeds the value of the dotted dash line gradually approaches zero.This is due to the fact that after entering the nonlinear growth phase, EDI extracts energy from ions with velocities exceeding the wave speed,leading it to further grow.The interaction between waves and ions reduces the proportion of velocities exceeding the wave speed in the velocity distribution.When the portion of ions with velocities exceeding the wave speed approaches zero,ions become trapped in potential wells.At this stage,the ion heating mechanism of EDI is disrupted,and the ability to gain energy through wave-particle interaction is suppressed.Consequently,the EDI enters a quasisteady state where ions no longer interact with the wave, and ion energy tends to stabilize.
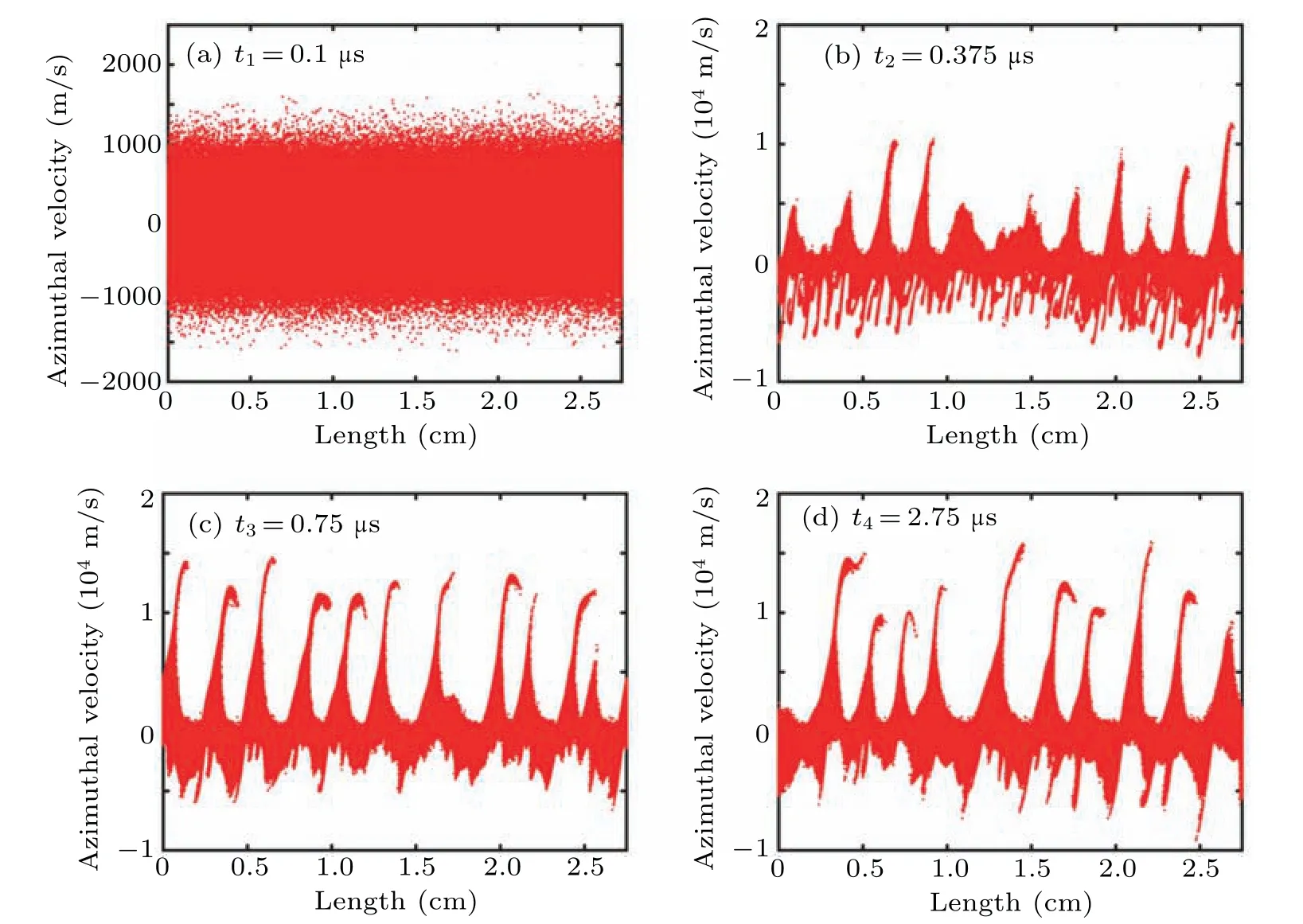
Fig.6.Evolutions of ion phase space in azimuthal direction at different time points.
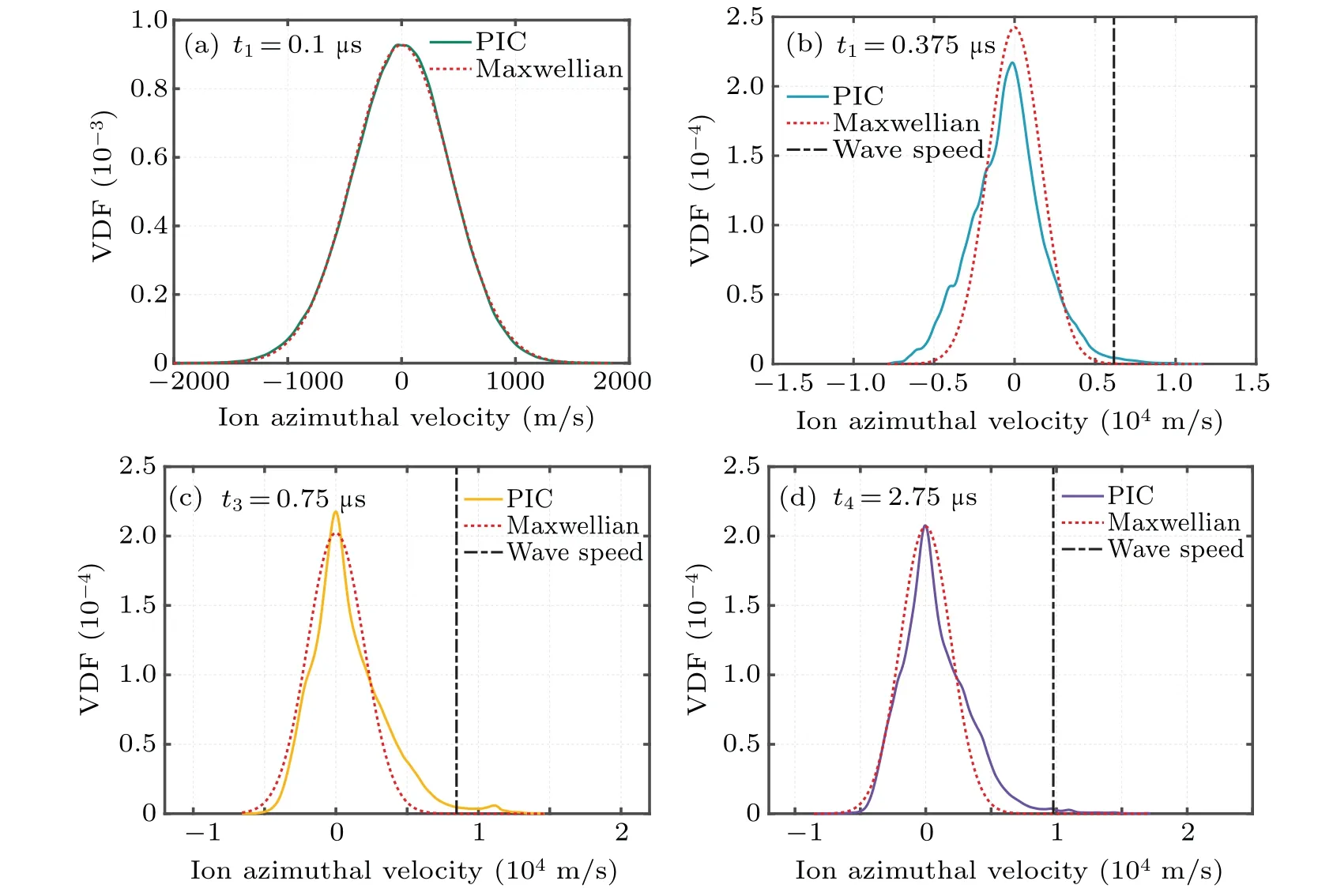
Fig.7.Fitting of ion azimuthal velocity distributions at different time points.
3.2.Effect of propellant type on EDI
In this study, three different types of propellants,Ar,Kr,and Xe,are selected to investigate their influences on the EDI.The variations in the mass of the propellant ions, atomic ionization energy, and scattering cross-section are considered.Only the collisions between electrons and neutral particles,including elastic, excitation, and ionization collisions, are considered under different types of propellants.
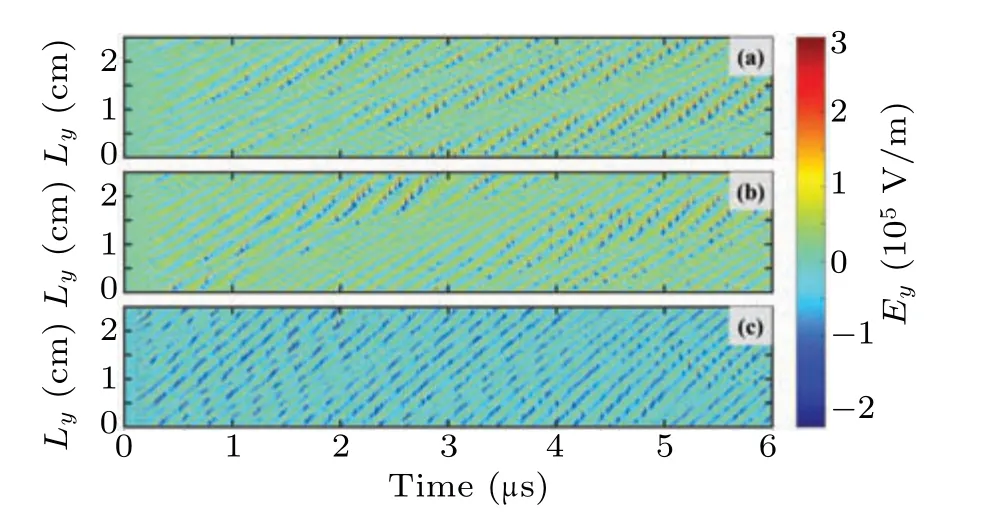
Fig.8.Spatiotemporal distribution of angle electric fields with different propellants: (a)Xe,(b)Kr,and(c)Ar.
Figure 8 displays the spatial and temporal distributions of the azimuthal electric field with different propellants.It can be observed from the figure that changing the propellant type does not have a significant inhibitory effect on the generation of EDI,as the oscillations of the azimuthal electric field occur nearly simultaneously in different propellants.Table 3 shows the duration, initial amplitude, and linear growth rate of the oscillatory linear growth phase of EDI with different propellants,with the linear growth rate normalized by the ion plasma frequency of Xe+.From the table,it can be observed that as the ion mass decreases, the linear growth duration of EDI gradually decreases and the initial amplitude decreases,the linear growth rate increases.This is due to the lighter ions being more susceptible to the effect of electron–ion friction,resulting in an earlier onset of EDI and a faster growth in its amplitude.The oscillation amplitude,frequency,phase velocity, and ion temperature are shown in Figs.9 and 10 to study the influences of different propellants on the EDI.
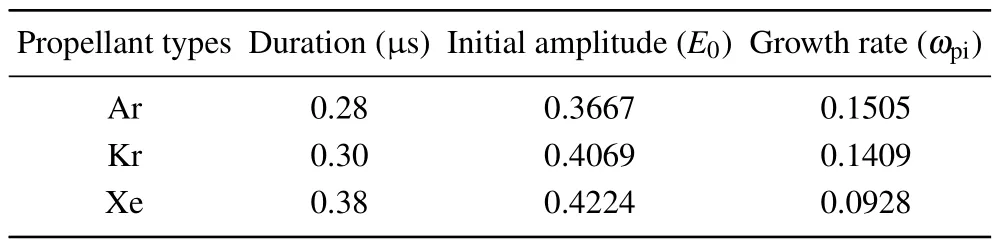
Table 3.Durations,initial amplitudes,and growth rates in EDI’s linear growth phase with different types of propellants.
Figure 9 shows the temporal evolutions of the amplitude of azimuthal electric field oscillation and the variations in frequency and phase velocity with different propellants.In this figure,the amplitude of oscillation is normalized by the axial electric field,and the frequency and phase velocity of the oscillation are analyzed as the system reaches a quasi-steady state.As shown in the figure, reducing the ion mass leads to faster attainment of a quasi-steady state in EDI,and it can effectively suppress the amplitude of oscillation after EDI has reached a quasi-steady state.Notably, the oscillations under Kr propellant and Ar propellant enter a large oscillation mode faster than under the Xe propellant.The frequency and phase velocity in the quasi-steady state of the EDI gradually increase as the ion mass decreases.The steady-state frequency of EDI oscillations in Ar, compared with that in Xe, increases by 30.23%,and the phase velocity increases by 30.22%.This is because ions with larger mass are not easily accelerated by the axial electric field,which leads to longer residence times of ions in the simulation region and longer EDI oscillation period, thus reducing the frequency.The lower acceleration and longer residence time of ions with heavier mass in the region also contribute to a decrease in the phase velocity of EDI oscillations.
Figure 10 shows the temporal evolutions of the average energy and azimuthal energy of particles for different propellants.From Fig.10 it is evidently seen that as the ion mass decreases,electron temperature deceases sightly.The total energy gained by ions from the axial electric field decreases and stabilizes more quickly.Moreover, the maximum energy of ions in the azimuthal direction increases, while the energy in the electron azimuthal direction gradually decreases.The ions are heated more rapidly in the azimuthal direction, resulting in a reduction in the amplitude of ion azimuthal energy oscillation during the second nonlinear growth phase of EDI and a faster transition to the quasi-steady state.However, after entering the quasi-steady phase, there is no significant change in the azimuthal energy of ions for different propellants.This indicates that the change in propellant types does not significantly affect the effectiveness of the ion heating mechanism of EDI.Additionally, with ion mass decreasing, ions become more susceptible to acceleration from the axial electric field and electron–ion friction.The former leads to the increase of axial acceleration,causing ions to exit from the simulation region more quickly.The latter results in a higher heating rate of ions in the azimuthal direction and facilitates faster interaction between ions and EDI.The faster interaction between ion and EDI wave enhances the possibility of ion capture,thereby suppressing the amplitude of ion energy oscillation and shortening the duration of the second nonlinear growth stage of EDI.Consequently,ions reach a steady state more rapidly.
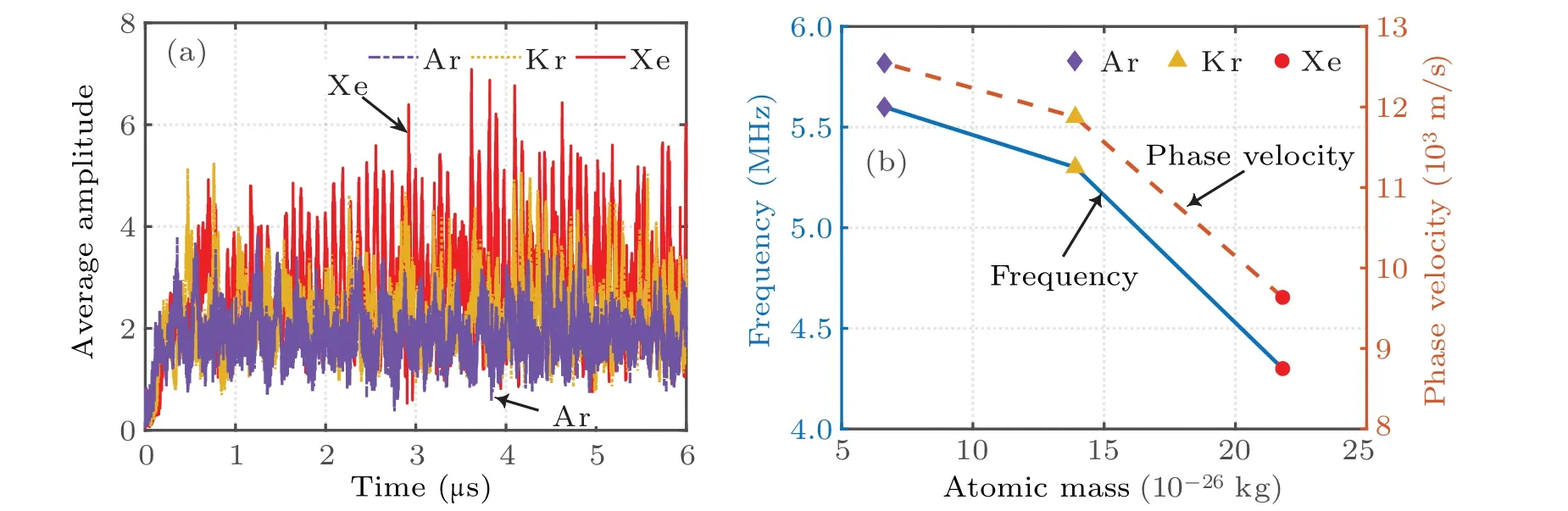
Fig.9.(a)Temporal evolutions of amplitude of azimuthal electric field oscillation and(b)variations of frequency and phase velocity of EDI with atomic mass for different propellants.
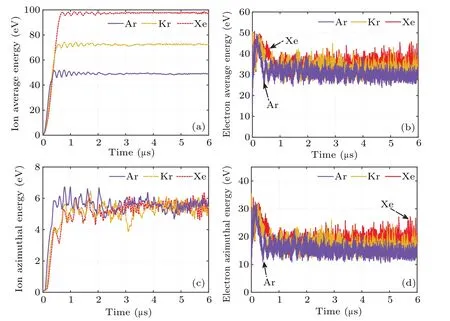
Fig.10.Variations of(a)ion average energy,(b)electron average energy,(c)ion azimuthal energy,and(d)electron azimuthal energy with time for different propellants.
3.3.Effect of EDI on axial electron mobility
EDI may be one of the main reasons for abnormal axial electron mobility.Considering the electron migration triggered by electrical drift instability, the classical electron mobility is corrected by introducing the electron momentum conservation equation as follows:[6,7,38]
wheremandqare the electron mass and charge,neandυdeare the electron density and drift velocity,respectively,andυmis the collision frequency of electrons with neutral atoms in the simulation region,Reiis the electron–ion friction force density,andΠerepresents the electron stress tensor.
By neglecting the electron–ion friction term in Eq.(2),the classical electron mobility due to collisions can be obtained as follows:[7,24]
whereωceis the electron cyclotron frequency, and the classical mobility of electrons in the simulation region is 0.0021 m2/(V·s)calculated from Eq.(3),which is in the same order of magnitude as the simulation results in Ref.[34].
By taking into consideration the influence of EDI, the axial electron migration rate, equation (2) can be expressed as[7,24]
When considering the influence of azimuthal electric field oscillation in EDI, the axial electron migration rate can also be expressed as follows:[7,24]
Furthermore,in this study,the actual axial electron mobility in the simulation region is calculated by working out the average axial electron velocity in the simulation region:
wherevjzis the the axial component of the electron velocity,Nis the number of electrons in the simulation region,andE0is the axial electric field set by the model.The ion heating mechanism is a complex process influenced by various factors, making it challenging to be analyzed quantitatively.By comparing Eq.(4)with Eq.(5),the electron–ion friction force density can be expressed as[7]
In the study the parameterReiis used as a measure of the response of the EDI to the heating capacity of ions in the azimuthal direction.It is described in Ref.[34]as follows:
whereCsis the ion sound velocity.In this simulation,the initial velocity of ions is very low, and uniformly distributed in the azimuthal direction and the radial direction.Thus,the expression ofReican be rewritten as[9]
Therefore, combining Eqs.(4) and (10), it can be concluded that the axial electron migration rate can also be expressed under the condition satisfied by Eq.(10)as follows:[38]
Figure 11(a) shows the axial electron mobility in the simulation region within the 2-μs interval for different propellants after the EDI has reached the quasi-steady state.The axial electron mobility is calculated from Eqs.(5) and(7).From the figure, it can be observed that the axial electron mobility for Xe propellant in the simulated region is 9.98 m2/(V·s), which is consistent with the result reported in Ref.[23].When considering the actual differential scattering cross-section, the axial electron mobility fluctuates within a range of 9.98 m2/(V·s)–11.50 m2/(V·s),showing no significant variation with change in the type of propellant.This indicates that changes in the type of propellant will not significantly affect the axial electron mobility at the exit of the thruster discharge channel.Figure 11(b)depicts the variation in axial electron mobility when neglecting change in the differential scattering cross-section, yielding similar results to those reported by Asadiet al.[23]which demonstrates that increasing the ion mass can suppress the axial electron mobility effectively.This is attributed to the fact that neglecting the chnges in differential scattering cross-sections can distort the electron energy loss caused by collisions in the model.By combining
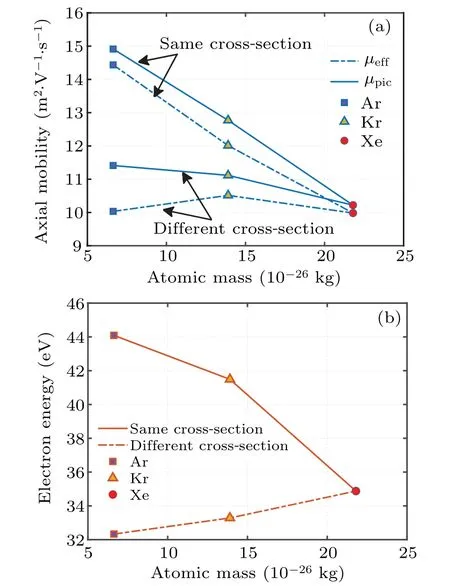
Fig.11.Variations of(a)axial electron mobility and(b)electron energy with atomic mass for different propellants.
Fig.10(b)with Fig.12,it can be observed that Xe atoms predominantly experience elastic collisions with electrons in the simulation region.But Ar atom and Kr atom exhibit a higher frequency of excitation collisions with electrons, leading to more significant electron energy losses.Referring to Eqs.(8)–(10), it becomes evident that change in electron temperature directly influences variation inRie,subsequently leading to the variation of axial electron mobility.As depicted on the vertical axis of Fig.11,the electron temperature variation resulting from change in scattering cross-sections align with the corresponding trends in axial electron mobility under respective conditions.
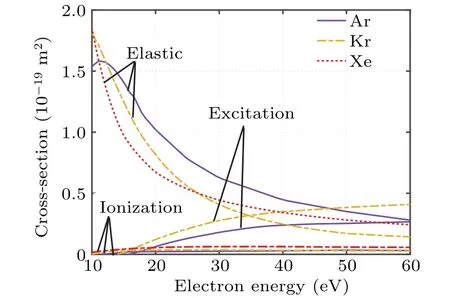
Fig.12.Variations of differential scattering cross-sections with electron temperature for different propellants.
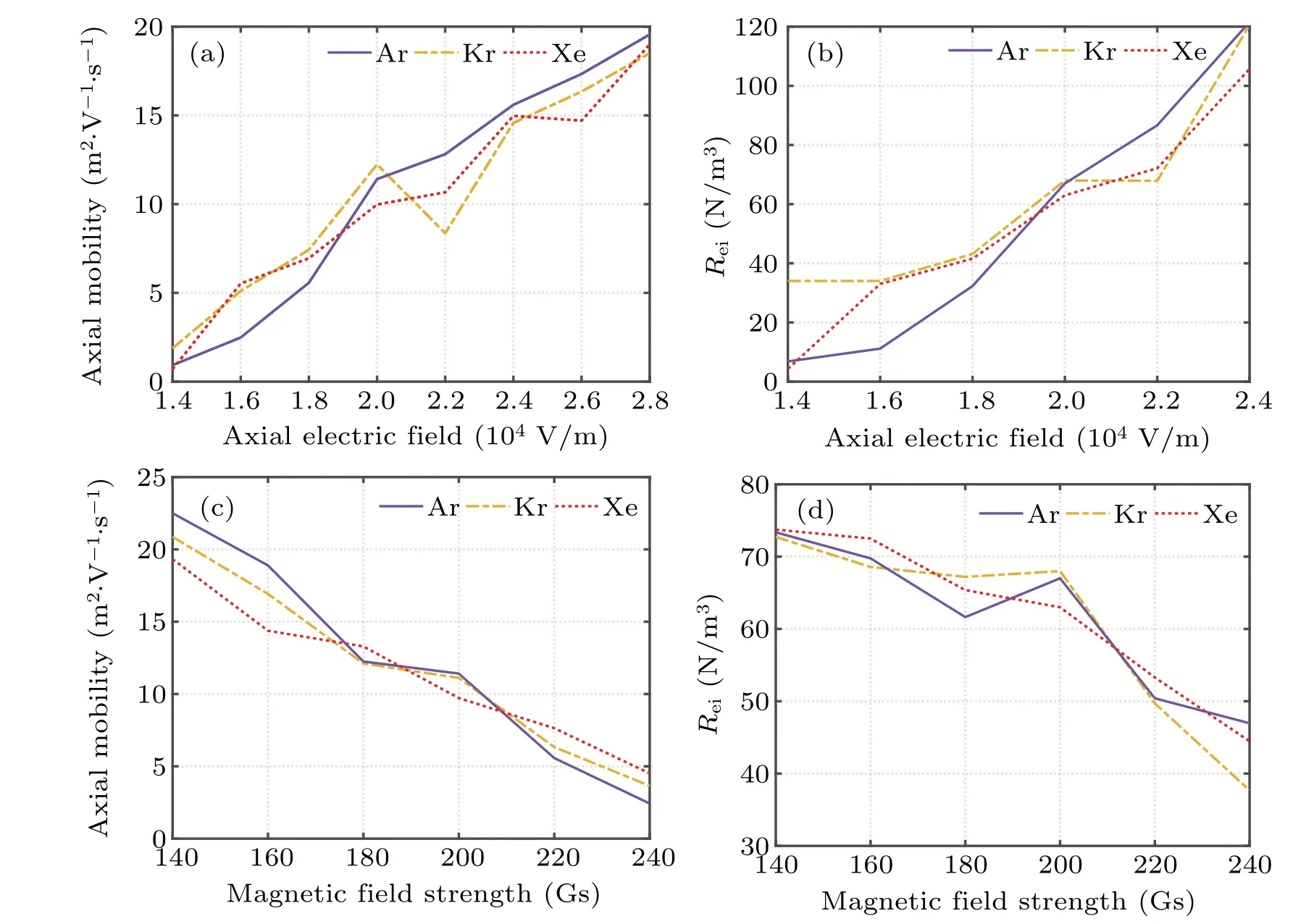
Fig.13.Variations of(a)axial electron mobility and(b)electron–ion friction force density with electric field strength for different propellants;variations of(c)axial electron mobility and(d)electron–ion friction force density with magnetic field for different propellants.
Figure 13 shows the variations of axial electron mobility and the corresponding electron–ion friction force density with the applied electric and magnetic field strength for different propellants.It can be observed from Fig.11 that the axial electron mobility calculated from Eqs.(5) and (7) exhibit good consistency, therefore figure 13 only displays the axial electron mobility calculated from Eq.(7).As shown in Figs.13(a)–13(c), smaller axial electric field and larger magnetic field can effectively suppress the axial electron mobility.This aligns with the conclusion drawn from the experimental findings in Ref.[42].Changes in types of propellants with external electric strength and magnetic field strength do not have a significant influence on the axial electron mobility.According tovde~E/B, the increase in electric field strength and the decrease in magnetic field strength both result in a larger drift velocity of electrons in the azimuthal direction.Moreover, the smaller magnetic field strength also results in the lager electron cyclotron drift radius.This weakens the ability of the electromagnetic field to bind the electrons,allowing the electrons to quickly pass through the simulation region.As illustrated in Figs.13(b) and 13(d), the enhancement of the electron–ion friction force density further promotes the increase in axial electron mobility.
4.Conclusions
This study focuses on the physical processes of the electron drift instability in the near-exhaust region of Hall thruster channel.A 1D physical model is established, and the generation,development,and saturation process of EDI,as well as its influence on particle energy and density, are numerically studied by using particle-in-cell simulation.The influences of different propellants on the EDI and axial electron mobility are also discussed.The obtained results are given below.
During the linear growth phase, EDI exhibits a significant ion heating mechanism in the azimuthal direction through electron–ion friction,resulting in ion acceleration.In the nonlinear growth phase,EDI wave speed is similar to the ion velocity and further grows to reach a quasi-steady state through the Landau damping effect.However,the ion heating mechanism of EDI becomes ineffective due to the ion wave trapping effect caused by Landau damping.
The choice of propellant in Hall thruster can affect the frequency and amplitude of the EDI oscillation greatly.Increasing the mass of the propellant prolongs the duration of the linear growth phase of EDI and reduces the linear growth rate of the amplitude.Comparing with Xe as the propellant, the linear growth rate of the amplitude of EDI under Ar decreases by 38.34%.Once EDI reaches a quasi-steady state,the smaller ion mass leads to higher frequency and smaller amplitude of EDI oscillation.Comparing with Xe,the oscillation frequency and phase velocity of EDI under Ar increases by 30.23%and 30.22%,respectively.
The EDI can lead to an abnormal increase in the axial electron mobility by increasing electron–ion friction force.Variations in propellant type,with the actual differential scattering cross-section considered, are not sufficient to cause a significant change in the axial electron mobility.Additionally,smaller electric field and higher magnetic field strengths can effectively suppress the axial electron mobility.It is consistent with relevant experimental research results.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.11975062 and 11605021) and the Fundamental Research Funds for the Central Universities(Grant No.3132023192).
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

