形式三角矩陣環(huán)上的Gorenstein FP-內(nèi)射模及維數(shù)

吳德軍, 周 慧

(蘭州理工大學(xué) 理學(xué)院, 甘肅 蘭州 730050)

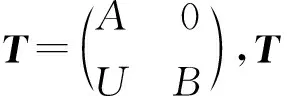
本文用pdRM,G-FP-idRM分別表示左R-模M的投射維數(shù)和Gorenstein FP-內(nèi)射維數(shù).pdRM<∞表示左R-模M的投射維數(shù)有限,HomR(X,Y)表示R-模X到Y(jié)的同態(tài)集.Maurice等[1]給出了形式三角矩陣環(huán)T的一些性質(zhì),例如:

1)T是左 Artin環(huán)當(dāng)且僅當(dāng)A,B是左Artin環(huán)且U是有限生成的B-模;

2)T是右 Artin環(huán)當(dāng)且僅當(dāng)A,B是右Artin環(huán)且U是有限生成的A-模;

3)T是Artin代數(shù)當(dāng)且僅當(dāng)存在交換環(huán)R,使得A,B是ArtinR-代數(shù)且U是有限生成的R-模.Mao等[2]介紹和研究了Gorenstein FP-內(nèi)射模,并將Gorenstein同調(diào)性質(zhì)從左諾特環(huán)擴充到了左凝聚環(huán)上.Zeng等[3]討論了Gorenstein FP-內(nèi)射模的性質(zhì),并且證明了若環(huán)R是左諾特環(huán)當(dāng)且僅當(dāng)每個Gorenstein FP-內(nèi)射左R-模是Gorenstein內(nèi)射左R-模.Gao等[4]給出了Gorenstein FP-內(nèi)射模的新定義并且從Gorenstein FP-內(nèi)射模的角度研究了自FP-內(nèi)射凝聚環(huán).2014年,Enochs等[5]研究了三角矩陣環(huán)上的Gorenstein投射模和Gorenstein內(nèi)射模及Gorenstein正則環(huán).楊燕妮等[6]證明了當(dāng)環(huán)R是右凝聚環(huán)且是右GFPI-封閉環(huán)時,Gorenstein FP-內(nèi)射右R-模是內(nèi)射可解類,并且給出了Gorenstein FP-內(nèi)射維數(shù)的若干等價刻畫.Mao[7]研究了形式三角矩陣環(huán)上的對偶對和FP-內(nèi)射模及維數(shù).吳德軍等[8]介紹和研究了投射余分解 Gorenstein平坦復(fù)形.受以上文獻的啟發(fā),本文討論了形式三角矩陣環(huán)上的Gorenstein FP-內(nèi)射模及維數(shù).

定義1[4]稱左R-模M為Gorenstein FP-內(nèi)射模,如果存在FP-內(nèi)射左R-模的正合列

Ε∶…→E1→E0→E0→E1→…

使得M?ker(E0→E1),并且對任意投射維數(shù)有限的有限表示左R-模P,HomR(P,Ε)正合.

引理1[4]設(shè)R是左凝聚環(huán),M是左R-模,則M是Gorenstein FP-內(nèi)射左R-模當(dāng)且僅當(dāng)存在FP-內(nèi)射左R-模的正合列

Ε∶…→E1→E0→E0→E1→…

使得M?ker(E0→E1).

定義2[6]稱環(huán)R為左GFPI-封閉環(huán),如果Gorenstein FP-內(nèi)射左R-模類對擴張封閉.

定義3[6]左R-模M的Gorenstein FP-內(nèi)射維數(shù),G-FP-idRM,定義為G-FP-idRM=inf{n|存在左R-模的正合列0→M→E0→E1→…→En→0,其中每個Ei是Gorenstein FP-內(nèi)射模}.

G-FP-idRM≤n當(dāng)且僅當(dāng)存在左R-模的正合列0→M→E0→E1→…→En→0,其中每個Ei是Gorenstein FP-內(nèi)射模.

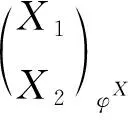
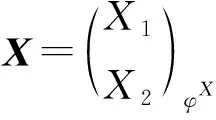
引理5[7]設(shè)A,B是左凝聚環(huán),UA是平坦模,BU是有限表示模.若G是FP-內(nèi)射左B-模,則HomB(U,G)是FP-內(nèi)射左A-模.

引理6設(shè)A,B是左凝聚環(huán),UA是平坦模,BU是投射維數(shù)有限的有限表示模.若G是Gorenstein FP-內(nèi)射左B-模,則HomB(U,G)是Gorenstein FP-內(nèi)射左A-模.

證明因為G是Gorenstein FP-內(nèi)射左B-模,所以存在FP-內(nèi)射左B-模的正合列

使得G?ker ?1,并且對任意投射維數(shù)有限的有限表示左B-模F,HomB(F,Λ)正合.由引理5知,HomB(U,Ni)為FP-內(nèi)射左A-模.

因為BU為投射維數(shù)有限的有限表示模,所以由定義1,HomB(U,Λ)正合.進而有FP-內(nèi)射左A-模的正合列

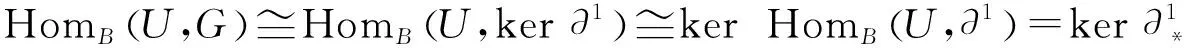
定理1BU是投射維數(shù)有限的有限表示模,考慮下列條件:

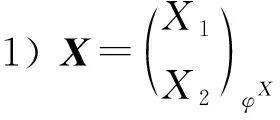
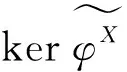
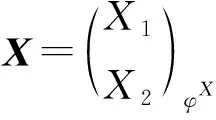
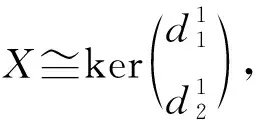
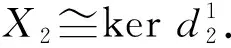
設(shè)pdBC=n<∞,則存在左B-模的正合列

0→Pn→…→P0→C→0

其中Pi(i=0,1,…,n)為投射模.進而存在左T-模的正合列

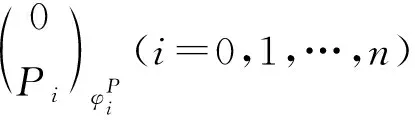
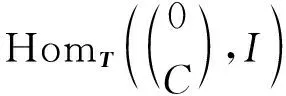
所以HomB(C,I2)正合.進而由定義1,X2是Gorenstein FP-內(nèi)射左B-模.

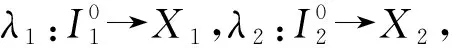
是滿同態(tài).考慮下面交換圖,如圖1所示.

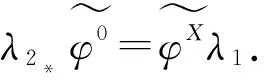
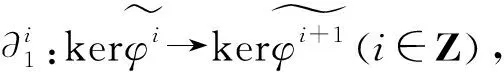
下證:對任意投射維數(shù)有限的有限表示模AD1,HomA(D1,E)正合.

對pdAD1<∞進行歸納:

當(dāng)pdAD1=0時,D1為投射模,進而HomA(D1,E)正合.假設(shè)當(dāng)pdAD1≤m時,HomA(D1,E)正合.當(dāng)pdAD1=m+1時,存在左A-模的正合列

0→L1→Q1→D1→0

其中Q1為投射模且pdAL1≤m.用HomA(-,E)作用上正合列,則有復(fù)形正合列, 如圖3所示.

因為Q1是投射模,所以HomA(Q1,E)正合.又因為pdAL1≤m,所以由歸納假設(shè),HomA(L1,E)正合,進而HomA(D1,E)正合.

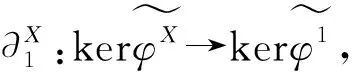
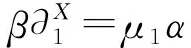
又因為X2是Gorenstein FP-內(nèi)射左B-模,所以存在FP-內(nèi)射左B-模的正合列

使得X2?kerd1,并且對任意投射維數(shù)有限的有限表示左B-模N,HomB(N,I)正合.因為BU是投射維數(shù)有限的有限表示模,所以HomB(U,I)正合,進而有左T-模的正合列

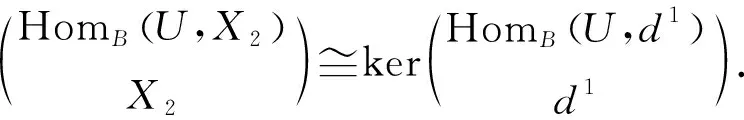
對pdTL<∞進行歸納:

當(dāng)pdTL=0時,L為投射模,進而HomT(L,Λ)正合.假設(shè)當(dāng)pdTL≤m時,HomT(L,Λ)正合.當(dāng)pdTL=m+1時,存在左T-模的正合列

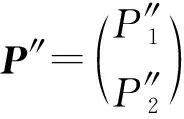
因為P″是投射模,故HomT(P″,Λ)正合.又因為

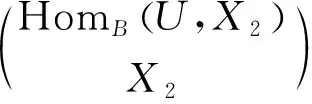
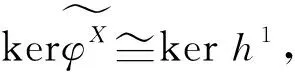
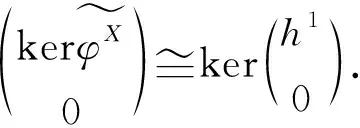
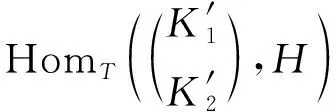
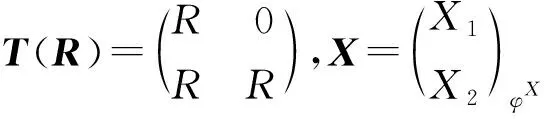
1)X是Gorenstein FP-內(nèi)射左T(R)-模;

此外,若R為左凝聚環(huán),則上述條件等價于:

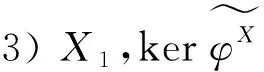
證明因為RR是有限生成投射模,所以RR是有限表示模.進而由定理1知,1)?2).

又因為R是左凝聚環(huán)且是左GFPI-封閉環(huán),所以由文獻[6]中命題1.4知,Gorenstein FP-內(nèi)射左R-模是內(nèi)射可解類.進而X1是Gorenstein FP-內(nèi)射左R-模當(dāng)且僅當(dāng)X2是Gorenstein FP-內(nèi)射左R-模.

推論2T是左GFPI-封閉環(huán),BU是投射維數(shù)有限的有限表示模,則每個Gorenstein FP-內(nèi)射左T-模是內(nèi)射模當(dāng)且僅當(dāng)每個Gorenstein FP-內(nèi)射左A-模是內(nèi)射模,每個Gorenstein FP-內(nèi)射左B-模是內(nèi)射模.

證明必要性:設(shè)X1是Gorenstein FP-內(nèi)射左A-模,X2是Gorenstein FP-內(nèi)射左B-模.

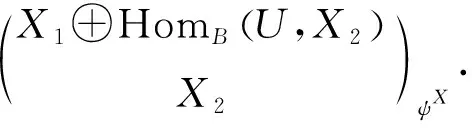
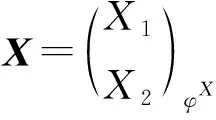
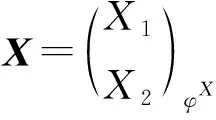
1) max{G-FP-idA(X1),G-FP-idB(X2)}≤G-FP-idT(X)≤max{G-FP-idA(X1),G-FP-idB(X2)+1};

2) max{lG-FP-id(A),lG-FP-id(B)}≤lG-FP-id(T)≤max{lG-FP-id(A),lG-FP-id(B)+1}.

證明1) 先證:max{G-FP-idA(X1),G-FP-idB(X2)}≤G-FP-idT(X).

假設(shè)G-FP-idT(X)=m<∞,則存在左T-模的正合列

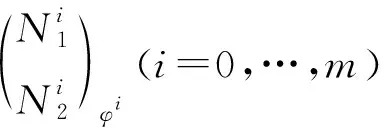
正合,所以G-FP-idA(X1)≤m,G-FP-idB(X2)≤m.

下證:G-FP-idT(X)≤max{G-FP-idA(X1),G-FP-idB(X2)+1}.

假設(shè)max{G-FP-idA(X1),G-FP-idB(X2)+1}=n<∞,則存在左B-模的正合列

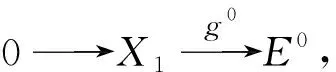
則h0是單同態(tài).從而有左T-模的正合列

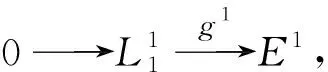
則h1是單同態(tài).從而有左T-模的正合列

重復(fù)以上過程,得到左T-模的正合列

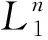
2) 由1)可得.

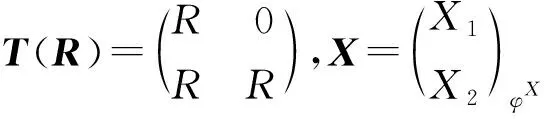
1) max{G-FP-idR(X1),G-FP-idR(X2)}≤G-FP-idT(R)(X)≤max{G-FP-idR(X1),G-FP-idR(X2)+1};

2) max{lG-FP-id(R),1}≤lG-FP-id(T(R))≤lG-FP-id(R)+1.

證明1) 因為T(R)是左GFPI-封閉環(huán),所以R是左GFPI-封閉環(huán).又因為R是左凝聚環(huán),RR是投射模,RR是有限生成投射模,所以由定理2可得.

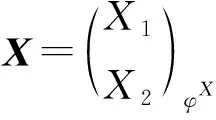
證明由定理2可得.