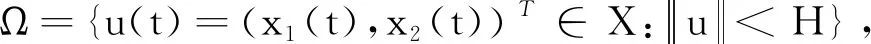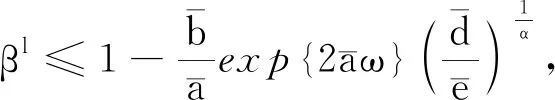具避難所和Rosenzweig功能性反應的兩種群捕食-食餌系統(tǒng)的周期正解

吳玉敏, 李福坤

(1.山東石油化工學院 基礎科學學院,山東 東營 257061;2.山東石油化工學院 機械與控制工程學院,山東 東營 257061)

眾所周知,避難所對捕食-食餌系統(tǒng)的動力學行為有著重要的影響,近年來許多學者在這一課題上展開研究(文獻[1—11]),其中有關自治系統(tǒng)的平衡點的存在性與局部穩(wěn)定性,極限環(huán)的存在性、唯一性和穩(wěn)定性,Hopf分支產(chǎn)生的可能性等,已經(jīng)有很好的成果.眾所周知,自然界中生物的生存環(huán)境都是隨著時間變化而不斷變化的,現(xiàn)實生存環(huán)境中定常系統(tǒng)基本不存在,因此非自治生態(tài)系統(tǒng)顯得更為合理.早在1997年,有關非自治具有避難所的捕食-食餌種群的動力學行為就有學者提出并加以研究[9],然而這方面的研究進展并不如自治模型的研究來得深入.文獻[8—9]均是以經(jīng)典的Lotka-Volterra捕食食餌模型為基礎提出的模型,我們知道,Lotka-Volterra模型由于其線性化假設,一直受到學者們的詬病,文獻[1—5]開始考慮捕食者的功能性反應對具有避難所的捕食-食餌系統(tǒng)的動力學行為的影響,他們分別研究了具有Holling Ⅱ、Holling Ⅲ類功能性反應和B-D功能性反應的捕食-食餌系統(tǒng)的動力學行為.在假設系統(tǒng)(1)的各項系數(shù)均為正常數(shù)下,Ma等提出了自治具有避難所和Rosenzweig功能性反應的兩種群捕食者-食餌系統(tǒng),探討了系統(tǒng)正平衡點的存在性和穩(wěn)定性,極限環(huán)的存在性等問題[10].本文將在文獻[10]的基礎上進一步考慮如下非自治具有避難所和Rosenzweig功能性反應的兩種群捕食者-食餌系統(tǒng):

(1)

為了下文敘述方便,對f∈C(R,R)且為ω周期連續(xù)函數(shù)引進記號:

1 預備知識

為了證明周期解的存在性,我們引入重合度理論中的延拓定理[11].

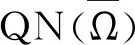
(ⅰ)對任意的λ∈(0,1),方程Lx=λNx的解滿足x??Ω∩DomL;

(ⅱ)對任意的x∈?Ω∩KerL,QNx≠0而且

deg{JQN,Ω∩KerL,0}≠0,

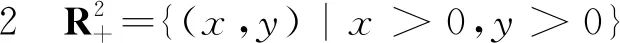
N1(t)=

N2(t)=

引理證畢.

2 主要結果及其證明

證明做變換Ni(t)=exp{xi(t)},i=1,2,則系統(tǒng)變?yōu)?/p>

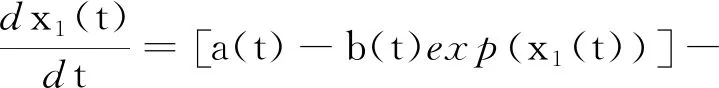
c(t)(1-β(t))αexpα-1(x1(t))exp(x2(t)),

(2)

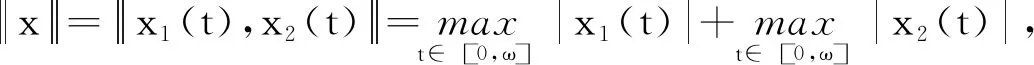
c(t)(1-β(t))αexpα-1(x1(t))

exp(x2(t))e(t)(1-β(t))αexpα(x1(t))-

則有

KerL={x∈X:x=h∈R2},

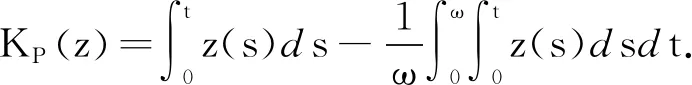
對應于算子方程Lx=λNx,λ∈(0,1)有

c(t)(1-β(t))αexpα-1(x1(t))exp(x2(t))],

(3)

設x=x(t)∈X是系統(tǒng)(3)的對應于某個λ∈(0,1)的解,將(3)式兩端同時從0到ω積分得

c(t)(1-β(t))αexpα-1(x1(t))exp(x2(t))}dt=0,

即

(4)

(5)

由(4)～(5)式可得

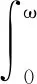
c(t)(1-β(t))αexpα-1(x1(t))exp(x2(t))|dt≤

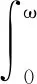
c(t)(1-β(t))αexpα-1(x1(t))exp(x2(t))|dt≤

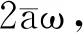
(6)

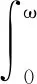
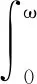
(7)

由(5)式和積分中值定理知,存在τ∈[0,ω],使得

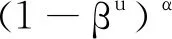
從而

|x1(τ)|≤

(8)

從而由(6)式和(8)式可得

(9)

進一步由(4)式和(9)式利用中值定理可知,存在η∈[0,ω],使得

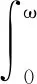
(10)

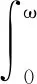
(11)

由此可知

|x2(η)|≤

(12)

從而由(7)式和(12)式可得

(13)

顯然Hi(i=1,2)的選取與λ的選取無關.令f(t)=c(t)(1-β(t))α,h(t)=e(t)(1-β(t))α,由定理條件知代數(shù)方程組

(14)

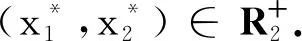
令H=H1+H2+H3,其中H3>0充分大,使