擴張的圈Schr?dinger-Virasoro 代數(shù)的二上同調群

王 松, 王曉明

(上海海洋大學信息學院,上海201306)

1 引言

眾所周知, Schr?dinger 代數(shù)和Virasoro 代數(shù)與非平衡統(tǒng)計物理密切相關, 它們在數(shù)學和物理學(如統(tǒng)計物理學) 的許多領域中都有著重要的作用. Schr?dinger-Virasoro 代數(shù)sb 最初是由Henkel 在研究自由Schr?dinger 方程的不變性時被引入文獻[1], 其結構和表示理論被Roger 和Unterberger 在文獻[2] 深入研究. 比如, Henkel 在文獻[1] 中給出了sb 只有一維中心擴張. Roger 和Unterberger 在研究sb 的同調理論時得出了有三維外導子[2]. sb 上的有限維不可約權模在文獻[3] 中被分類. 廣義的Schr?dinger-Virasoro 代數(shù)的自同構群及Verma 模被完全確定[4]. 最近幾年Schr?dinger-Virasoro 代數(shù)及其變形的結構和表示理論被許多學者廣泛研究[5?8]. 為了研究sb 的頂點表示, Unterberger 介紹了一類新的無限維李代數(shù)[9], 稱之為擴張的Schr?dinger-Virasoro 代數(shù)該李代數(shù)是復數(shù)域C 上的向量空間, 帶有一組基滿足李積關系

該無限維李代數(shù)的導子、自同構群及中心擴張等結構理論在文獻[10] 中被完全刻畫.

對任意的m,n,i,j ∈Z, 其中Lm,i表示Lm?ti, 其他定義類似.

由于李代數(shù)的二上循環(huán)在其中心擴張方面起著關鍵作用, 可以借助它構造許多無限維李代數(shù), 并且可以進一步刻畫所得李代數(shù)的結構及表示. 同時上同調群和李代數(shù)的結構密切相關, 比如一階同調群和李代數(shù)的導子代數(shù)及李雙代數(shù)的聯(lián)系, 從而上同調群的計算就顯得比較重要. 本文主要確定了擴張的圈Schr?dinger-Virasoro 代數(shù)的所有二上同調群, 并且給出了它的泛中心擴張. 我們希望借助于中心擴張能夠進一步深刻理解的結構及其表示.

2 擴張的圈Schr?dinger-Virasoro 代數(shù)的二上同調群

令φ=ψ ?ψf, 其中ψf即為(2.1) 式中的定義, 顯然很容易驗證

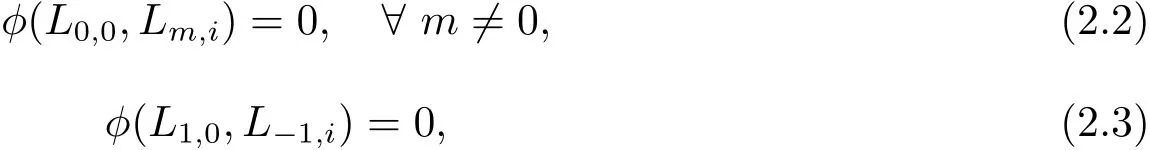
下面通過幾個引理給出主要結果.

引理2.1

證由二上循環(huán)φ 的關系知

整理得

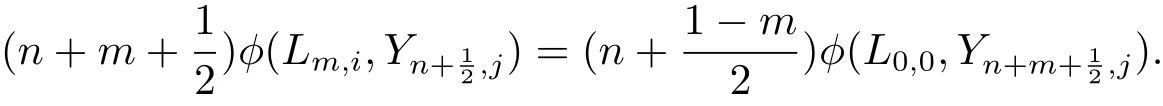
引理2.2

證由二上循環(huán)φ 的關系知

整理得

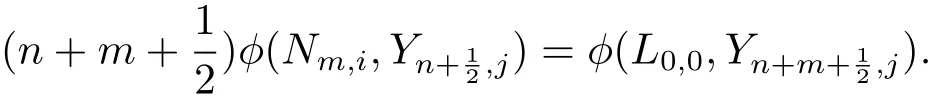
引理2.3

證由二上循環(huán)φ 的關系知

整理得

則有

引理2.4

證由關系

整理得

又由關系

整理得

取n=m, 則有

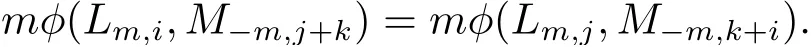
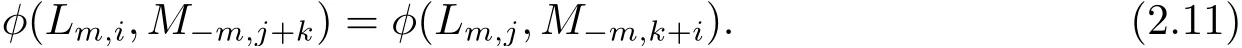
在(2.10) 式中令m=?n, 則有

從而

由(2.11) 和(2.12) 式, 得到

上式說明僅與第二個指標的和i + j + k 有關, 而與位置無關, 從而不妨設Am,i+j=φ(Lm,i+j,M?m,0). 在(2.10) 式中取m=1, 又由(2.5) 式有

在(2.14) 式中用n ?1 替換n, 則有

在(2.10) 式中取n=n ?1,m=2, 可得

將(2.14),(2.15) 和(2.16) 式聯(lián)立方程, 解得

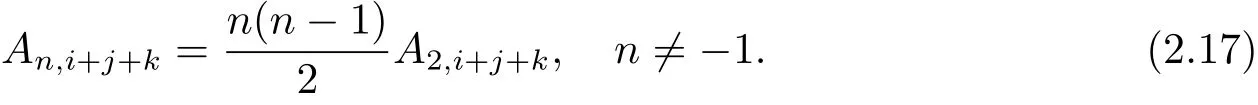
在(2.10) 式中令m=2,n=?1, 從而

由(2.17) 和(2.18) 式, 得到

考慮關系

又由關系

整理得到

在(2.21) 式中取m=0, 則有

在上式取n=?2, 結合(2.5) 式, 從而有

由(2.19),(2.22) 及(2.23) 式, 可得

上式也說明僅與第二個指標的和i+j+k 有關, 而與位置無關. 當n=?2 時, 由φ 的反對稱性及上式知

在(2.24) 式中分別取n=2,?3, 則有

由φ 的反對稱性知A2,i+j+k=0. 從而由(2.19), (2.24) 和(2.25) 式知

引理2.5φ(Mm,i,Mn,j)=0, ?m,n,i,j ∈Z.

證由于

從而有

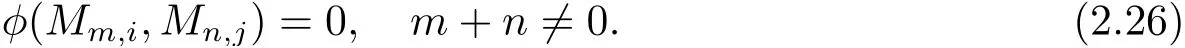
又由

則有

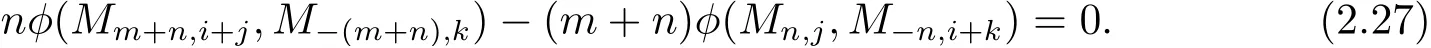
在(2.27) 式中令m=0, 則有

在(2.27) 式中令n=0, 可得

綜合(2.28) 和(2.29) 式, 有

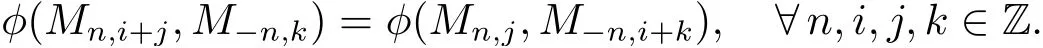
上式說明僅與第二個指標的和i + j + k 有關, 而與位置無關. 從而不妨令Bn,i+j=φ(Mn,i+j,M?n,0), 在式(2.27) 式中取n=1, 則有

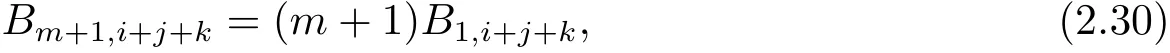
又由

從而

在上式中取m=2,n=?2, 可得B1,i+j+k=0, 由(2.30) 式知

綜合(2.26) 和(2.31) 式, 得到

引理2.6φ(Mm,i,Nn,j)=0, ?m,n,i,j ∈Z.

證由關系

從而由(2.4) 式得

又由關系

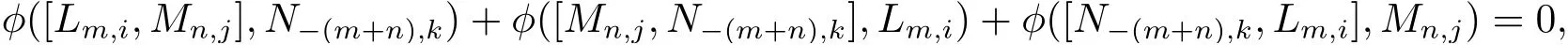
結合引理2.4, 整理得

若m=0, 則有

在(2.33) 式中令n=0, 可得

由(2.33) 和(2.35) 式, 有

上式說明僅與第二個指標的和i+j+k 有關,而與位置無關.不妨設Cn,i+j=φ(Mn,i+j,N?n,0),在(2.33) 中令n=1, 則有

又由關系

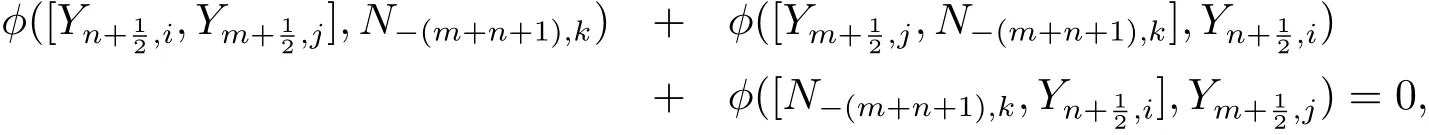
又由引理2.4, 整理得

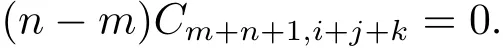
在上式令n=1,m=?1, 則有C1,i+j+k=0, 從而由(2.37) 式, 知

由上式結合(2.32) 式, 就可得到

引理2.7

證由關系

由(2.6) 式, 則有

又由關系

整理得

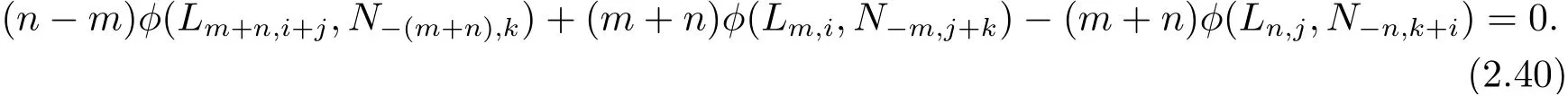
在上式中取m=n, 則有

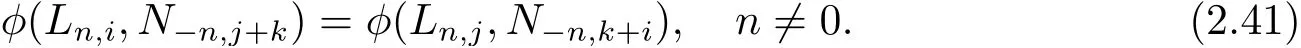
在(2.40) 式中取m=?n, 可得

由(2.41) 和(2.42) 式, 則有

上式說明僅與第二個指標的和i+j+k 有關,而與位置無關.不妨設Dn,i+j=φ(Ln,i+j,N?n,0),在(2.40) 式中取n=1, 結合(2.7) 式, 則有

在上式用m ?1 替換m, 有

在(2.40) 式中令n=2,m=m ?1, 得到

將式(2.44),(2.45) 和(2.46) 式聯(lián)立方程, 解得

在(2.40) 式中取m=2,n=?1, 結合(2.7) 式, 易得D2=D?1, 從而由(2.47) 式就有

由上式和(2.39) 式, 有

引理2.8φ(Nm,i,Nn,j)=δm+n,0mφ(N1,i+j,N?1,0), ?m,n,i,j ∈Z.

證由關系

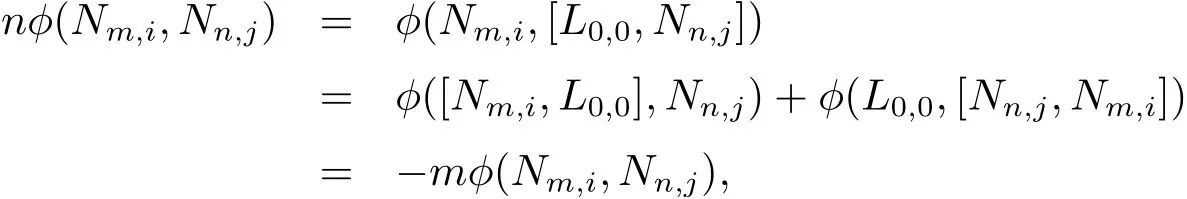
整理得

又由關系

從而有

在上式取m=0, 則有

在(2.49) 式中取m=?n, 可得

由(2.50) 和(2.51) 式, 有

上式說明僅與第二個指標的和i+j+k 有關,而與位置無關.不妨設En,i+j=φ(Nn,i+j,N?n,0),在(2.49) 式中令n=1, 就有

引理2.9

證由關系

由上式及(2.2) 式可得

考慮關系

整理得

在上式中令n=m, 則有

在(2.55) 式中取m=?n=1, 結合上式可得

由(2.56) 和(2.57) 式, 有

上式說明僅與第二個指標的和i+j+k 有關,而與位置無關.不妨設Fn,i+j=φ(Lm,i+j,L?m,0),在(2.55) 式中令m=1, 結合(2.3) 式, 則有

將上式n 由n ?1 替代, 從而

在(2.55) 式中取m=2,n=n ?1, 可得

將(2.59),(2.60) 和(2.61) 式聯(lián)立方程組, 解得

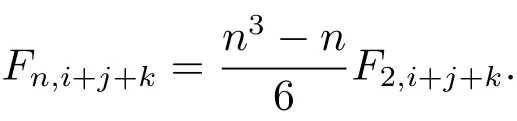
由引理2.1–2.9, 我們就可以得到本文的主要定理.

定理2.1二上同調群

注考慮中心擴張滿足李積關系: 對于任意給定的k ∈Z, 有