Robust Adaptive Gain Higher Order Sliding Mode Observer Based Control-constrained Nonlinear Model Predictive Control for Spacecraft Formation Flying

Ranjith Ravindranathan Nair and Laxmidhar Behera,

I.INTRODUCTION

T HE past few decades have witnessed tremendous advances in space science and satellite technology.It has revolutionized our know ledge and understanding of Earth’s diverse landscapes,with enormous scientific applications invarious fields ranging from biological and geological studies to disaster management.The low Earth orbiting(LEO)satellites have already proven their efficacy in imaging and remote sensing applications in prior missions,with their high resolution imaging capability,which may help in educing pivotal information in various applications.The wider area of coverage,coupled with the added advantages of smaller spacecraft formation,make the constellation of miniaturized satellites more preferable over a single large platform,in many real missions.

The success of the constellation observing system for meteorology,ionosphere,and climate(COSMIC)mission,a collaborative project of the National Space Organization(NSPO)in Taiwan,China and the University Corporation for Atmospheric Research(UCAR)in the United States,making use of a constellation of six LEO micro satellites,is an example for this.

A decentralized optimal control segment,with good disturbance rejection capability,is a prerequisite for the success of a spacecraft formation flying(SFF)mission.Most of the SFF control strategies depicted in literature,are derived from multi-robotic systems.A brief survey on various spacecraft formation flying control and guidance strategies has been provided in[1].In[2],Liu and Kumar deal with a digital control technique for the tracking control of spacecraft in formation,with network-induced communication delays and external disturbances.Sliding mode control is one of the robust techniques commonly used in formation control applications[3]?[5].In[6],Nairet al.deal with the formation control of multiple satellites using artificial potential field based path planning scheme,combined with adaptive fuzzy sliding mode control.A Lyapunov-based,robust,nonlinear,adaptive control law for the relative position control of spacecraft is depicted in[7].The design of consensus protocol for the time varying formation control of swarm systems is presented in[8]and[9].But in all these strategies,the optimality in control input cannot be guaranteed.A comprehensive survey on the distributed attitude coordination control,provided in[10],points out optimal fuel consumption as one of the key features to be considered in formation control problem.A linear quadratic regulator based approach applied to in plane satellite formation keeping using tangential maneuvers,is presented in[11],in which a linearized model is used,where the margin of stability is limited.In[12],McCamishet al.deal with a distributed control algorithm for a multi-spacecraft system using LQR technique,combined with artificial potential field based collision avoidance;but it is limited to close proximity operations.

Model predictive control(MPC)is a widely used planning based approach,in which the concept of prediction in control makes it unique from other optimal control strategies.An MPC technique,in which a distributed decision-making with systematic constraint handling,to operate a linear dynamic network,is proposed in[13].In[14],Xia and Zhang have utilized an MPC approach for the operation efficiency improvement in energy systems.Reference[15]depicts an MPC approach applied to a linearized spacecraft formation dynamics with sensing noise.There are only very few researches done in the area of SFF,using nonlinear model predictive control(NMPC)approach.Most of the works are based on linear MPC approach.An NMPC technique applied to a nonlinear submarine system,is presented in[16],where the finite horizon open loop optimization problem is solved online.A similar approach is also utilized in[17]for the formation control of multiple unmanned aerial vehicles,in which inequality constraints for control inputs,collision avoidance and obstacle avoidance are included in the optimization routine.In that case,the step size has been chosen heuristically based on the operating conditions.But it is not recommendable for complex systems with diverse,unpredictable operating conditions.Moreover,Karush-Kuhn-Tucker variables are used for handling the constraints.It may further increase the complexity of the optimization problem.In[18],Muske and Badgwell deal with an offset-free linear model predictive control,in which the plant model is augmented with a state space disturbance model.

The precision in position and velocity measurements are also crucial for the efficient performance of decentralized control and guidance segment.The relative positions of the spacecraft are measurable using inertial navigation systems,viz.GPS.Velocity can either be obtained from the Doppler shift,which needs more complex post processing for compensating the Doppler noise,or by differentiating the position.The latter one using conventional differentiation,will give more erroneous result,if there is noise in the original position measurements.A robust observer can be utilized for obtaining the velocity as well as disturbance estimates from the noisy position measurements.Among the various estimation schemes available in literature,higher order sliding mode(HOSM)based approach is found to be highly robust to disturbances and insensitive to parametric variations.Moreover,chattering in HOSM is very less compared to that of conventional sliding mode observers.

Different types of higher order sliding mode differentiator structures are available in[19]?[22].A second order super twisting sliding mode observer for state as well as disturbance estimation,along with robust distributed output feedback control scheme for an SFF system,are depicted in[23].In this work,the authors have used only radial and tangential plane linearized dynamics based on Hill’s equations,where the out-of-plane dynamics is decoupled.[22]deals with the simultaneous fault and disturbance reconstruction in a multiinput multi-output(M IMO)nonlinear system using a network of interconnected sliding mode observers,where a complex HOSM structure has been used.HOSM observer for unknown input reconstruction and state estimation,for a M IMO system is described in[24],where the observer structure is independent of the control input and Lipschitz constant.Also,a system dynamics,with total vector relative degree less than the total number of states,has been considered.In[25],Iqbalet al.propose a robust feedback linearization technique,in which an HOSM differentiator,incorporating Lebesgue measurable control input and Lipschitz constant,is used for approximating the dynamics in a single-input single-output(SISO)system.Similarly,a continuous sliding mode controller and an HOSM based disturbance observer are designed for the tracking control of air-breathing hypersonic vehicles in[26].In all the above works,the observer gains are precomputed off line,where trajectory convergence cannot be guaranteed,if the initial estimates are chosen arbitrarily,or if there are unexpected state jerks.

The objective of the present work is to develop a robust decentralized control scheme for the tracking control of LEO satellites in a leader-follower based formation.Here,we propose a robust NMPC technique with a real time finite horizon open loop optimization[16],[17]for achieving the same.A nonquadratic cost function[27]has been considered for incorporating the control constraints,which can reduce the additional burden of constraint handling in the optimization algorithm.The heuristic choice of step size in optimization algorithm is not recommendable in all operating conditions.Hence,an adaptive tuning algorithm has been derived for updating the step size,which may improve the convergence speed.We have applied the HOSM observer structure containing the Lipschitz constant and Lebesgue measurable control input[19],[25]for obtaining the disturbance as well as velocity estimates from noisy position measurements.The system dynamics,having a total vector relative degree equal to the total number of system states,has been considered.The system is transformed into canonical form using nonlinear coordinate transformation[24].For the observers with precomputed fixed gains,the convergence can be guaranteed,only when initial estimates are chosen in the neighborhood of the actual values of the states[28].Moreover,it may not cope with unexpected state jerks.To handle these issues,here,we have proposed adaptive tuning algorithms,derived on the basis of Lyapunov stability theory,for updating the observer gains.The disturbance as well as the velocity estimates from the HOSM disturbance observer have been utilized by the output prediction model,in the NMPC[16],[17].The prescribed differentiator structure has good estimation accuracy[19].The observer design is repeated with an alternate HOSM differentiator structure as well.Simulation studies are conducted for a two-spacecraft system,for different levels of perturbations,along with added random noise.The results are compared with that of two recent references[26]and[29]respectively.

The rest of this paper is organized as follows.In Section II,the adaptive gain HOSM based technique for state as well as disturbance estimation is presented.Section III deals with the complete NMPC algorithm.The nonlinear model,and the design of proposed HOSM based predictive controller for the SFF system,are provided in Section IV.Simulation results are provided in Section V to validate the robustness of the proposed control scheme.Conclusions are drawn in Section VI.

II.ADAPTIVE GA IN HIGHER ORDER SLIDING MODE OBSERVER

For the completeness of the discussion,we begin with the HOSM based state estimation technique,depicted in[19],[22],[24].Consider the following nonlinear system

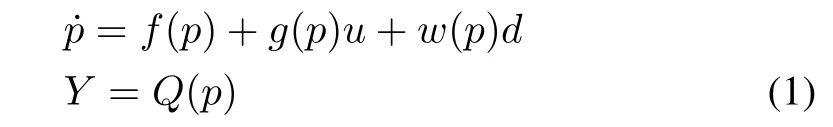
wheref(p)∈Rn,g(p)=[g1,g2,...,gm]∈Rn×m,Q(p)=[Q1,Q2,...,Qm]∈Rm,w(p)=[w1,w2,...,wm]∈Rn×m,p∈Rn,Y∈Rm,u∈Rmis the control input,andd∈Rmis the disturbance,defined in an open set Υ?Rn.The system with motion dynamics given by(1),is locally detectable,if the following conditions[24],[30]are satisfied,

Condition 1:The outputs of the system are assumed to have a vector relative degree,e={e1,e2,...,em},corresponding tow(p),if1,2,...,m,?k=1,2,...,ei?2,and

Condition2:M(p)=

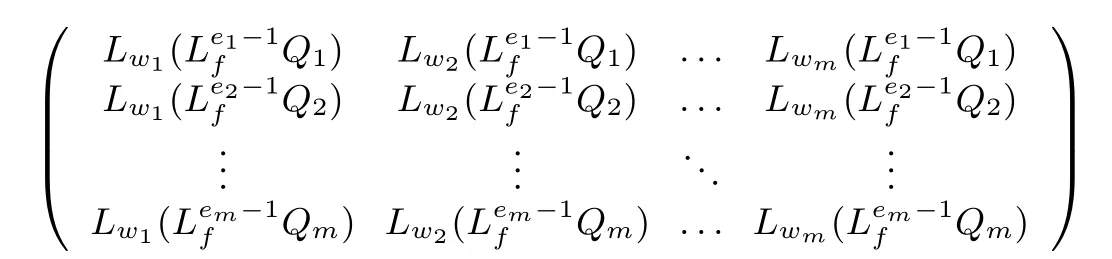
is nonsingular.

Condition 3:The distribution Λ =span{w1,w2,···,wm}is involutive.

These are necessary conditions for checking the observability of the nonlinear system in the presence of unknown inputs.The system given by(1)can be transformed into new coordinates as follows:?i=1,2,...,m,

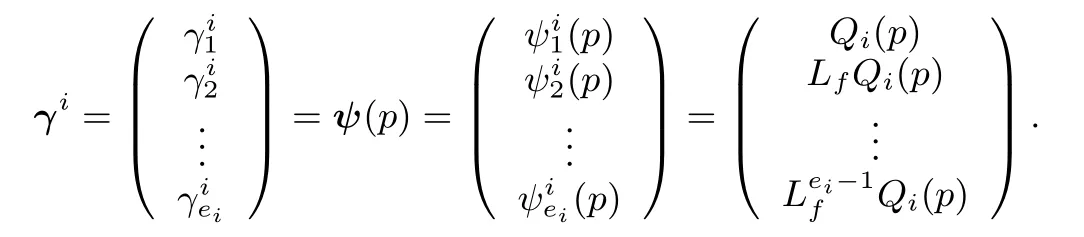
The transformation,x=ψ?1(γ),is a local diffeomorphism,since,it is described only in the neighborhood of any point,p,defined on an openset,Υ?Rn.Hence,the system given by(1)can be reformulated as

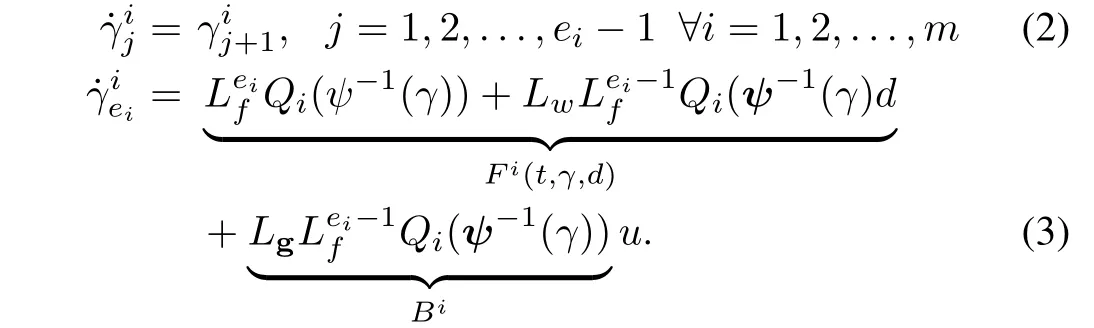
In this work,we have applied the HOSM differentiator structure[19],[25],incorporating the Lipschitz constant and Lebesgue measurable control input,to a complex multi-input multi-output system,to obtain the state as well as disturbance estimates from the noisy measurements.The observer gains are updated using adaptive tuning laws,derived based on Lyapunov stability theory.Hence the initial values of estimates can be chosen arbitrarily in the large compact subset of state space.Moreover,it can handle unexpected state jerks.Using the system canonical form[24]given by(2)and(3),the HOSM observer can easily be designed.Here,the system dynamics under consideration has a total vector relative degree equal ton.The HOSM differentiator structure is defined as follows[19],[25],

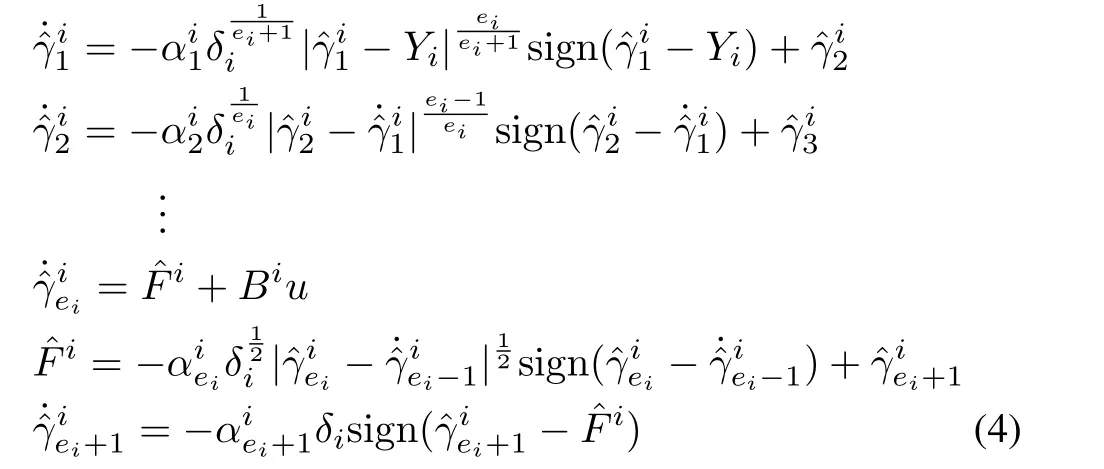
whereis the Lipschitz constant.

Theorem 1:Suppose that for the given nonlinear system,with the transformed dynamics as given in(2)and(3),and state observer structure as given in(4),the conditions(1)?(3)have been satisfied and the control input is Lebesgue measurable.Then,for any initial values of estimates chosen arbitrarily in the large compact subset of state space,the estimation error trajectories converge to origin along the sliding surface in finite time,if the observer gains are updated using the following adaptive tuning laws:

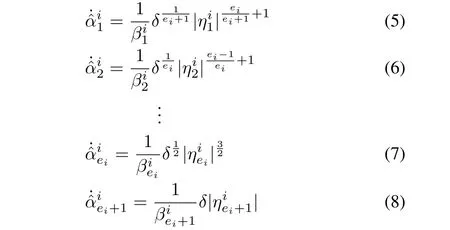
where

Proof:The estimation error can be defined as

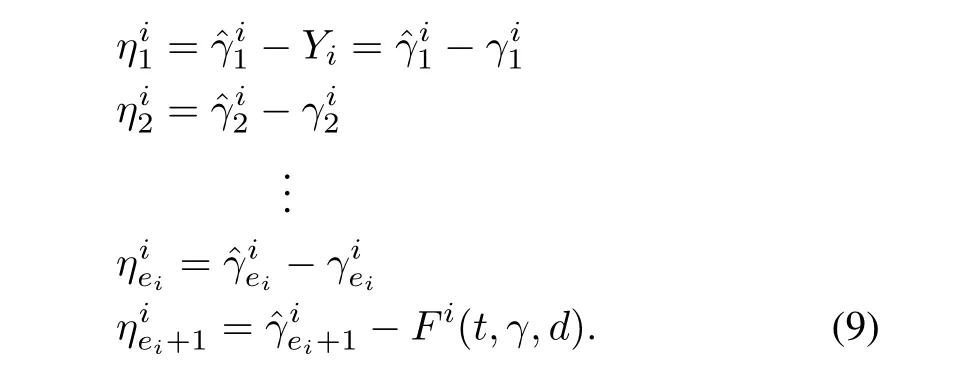
Since,

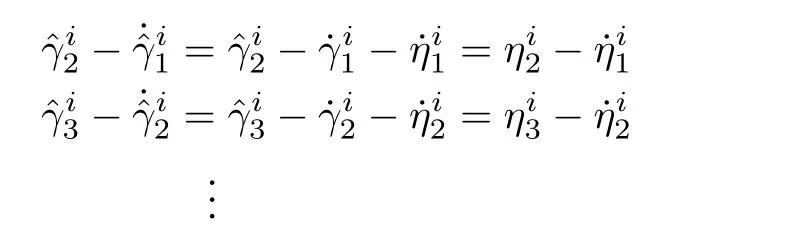
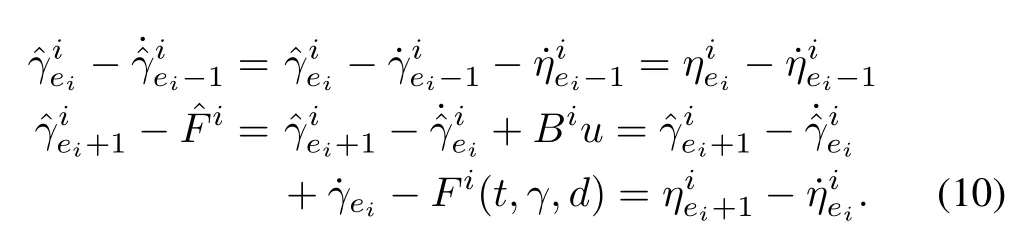
The error dynamics can be written as follows[31]:

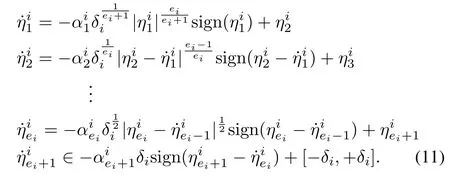
Step 1:For the time 0≤t≤t1,the Lyapunov candidate can be chosen as

Taking derivative of the Lyapunov function yields

Substituting for

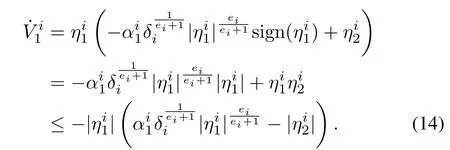
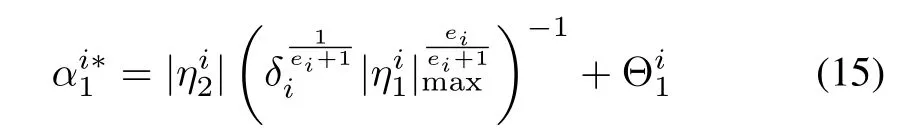
whererepresents the upper bound on the estimation error.Since the updation of gains and the convergence of the estimation error take place sequentially,remains constant at the initial value,during the time step,0≤t≤t1,for the given operating condition.The value of constantis chosen sufficiently high enough to ensure that the condition,always holds.HenceThe adaptation error can be defined as

The Lyapunov function can be modified as

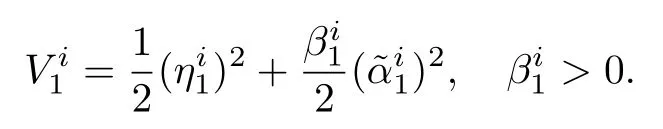
Hence,

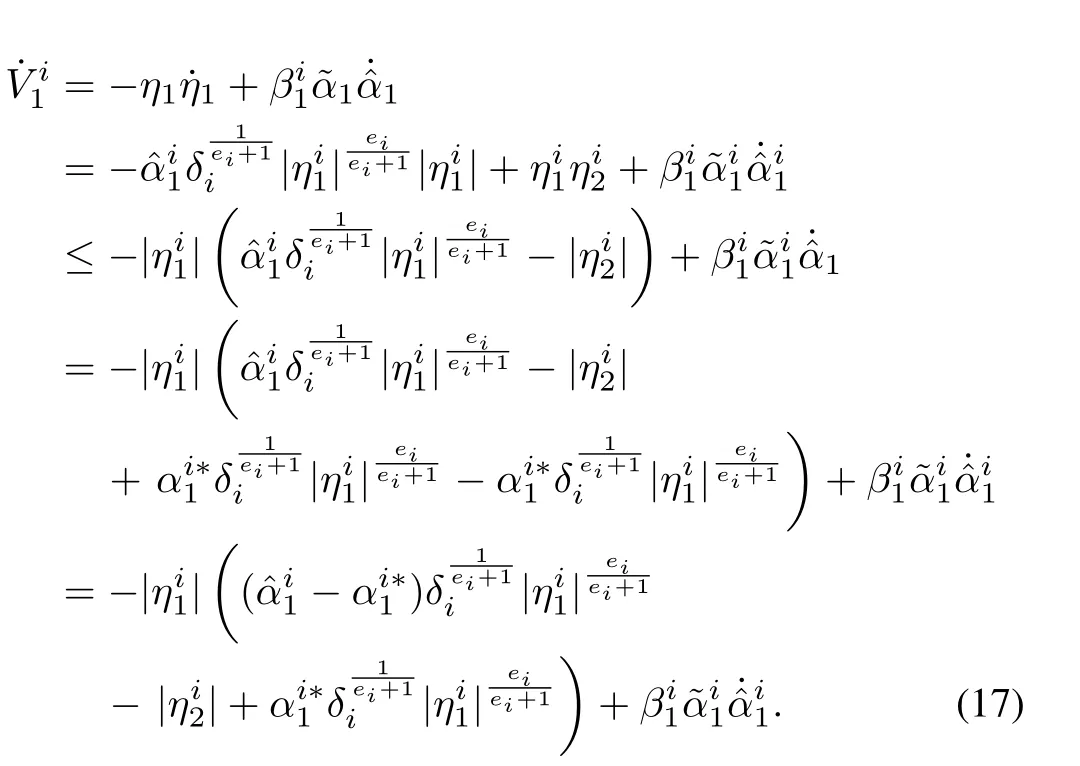
Substituting forfrom(15),

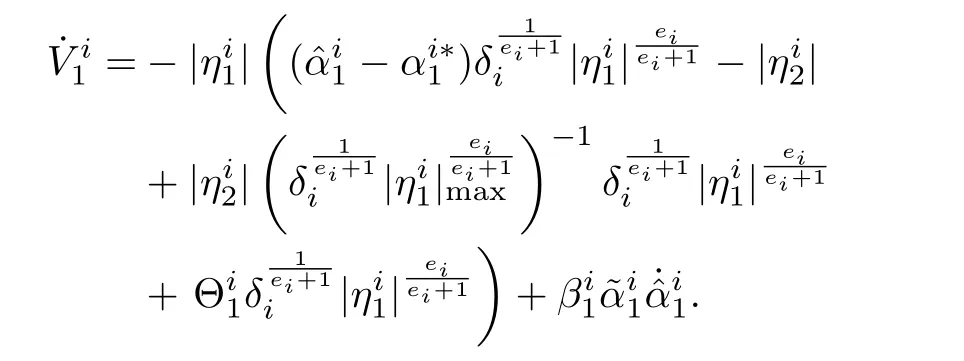
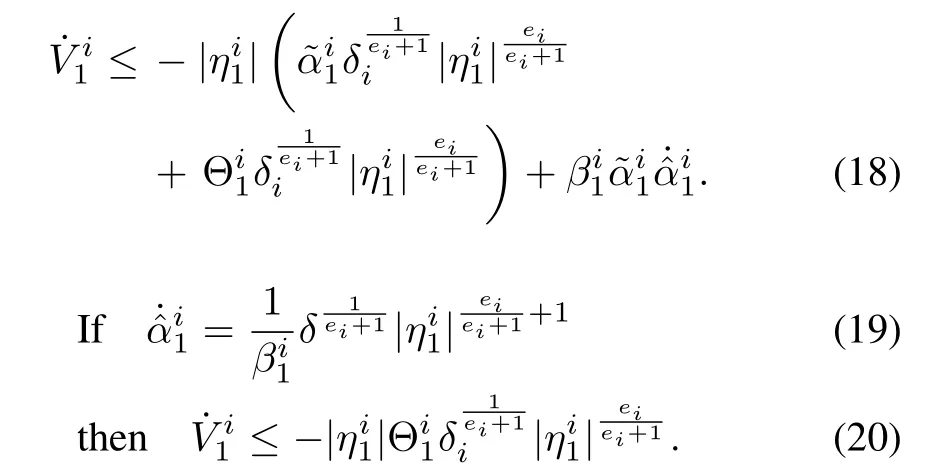
From(11),using Filippov theory[19],[31],we can find that the differential inclusion is consistent with the dilation,Hence it is homogeneous with a homogeneity degree of?1.Since the homogeneity degree is negative,the finite time convergence[19],[21],[25],[33]ofto zero can be guaranteed.The same has already been proved by Levant in[34],using the property of contractivity.Moreover,by Orlov’s theorem[33],[35],the finite time stability of the system can be guaranteed,if the system is asymptotically stable and the degree of homogeneityis negative.Since is uniformly continuous,the system is asymptotically stable.Hence,using Orlov’s theorem,the finite time stability can also be guaranteed,and the estimation error converges to zero in finite time sayt1,and the remaining error dynamics will converge to a hyper ball in finite time[32].

Step 2:For the timet1≤t≤t2,the remaining error dynamics becomes

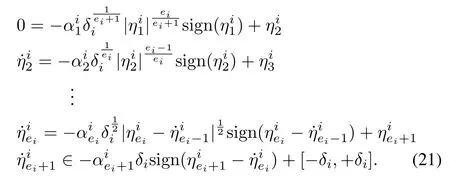
The Lyapunov candidate function can be chosen as

Taking derivative of the Lyapunov function and,substituting for˙ηi2,as in Step 1 yields

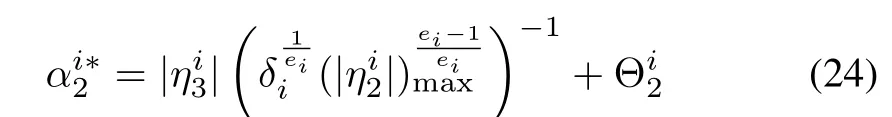
The Lyapunov function can be modified as

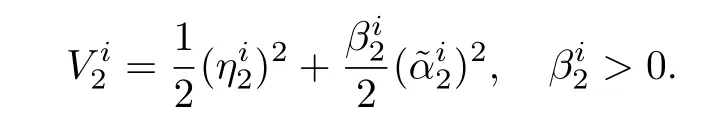
Taking the derivative of,and proceeding in the same way as in Step 1 yields,

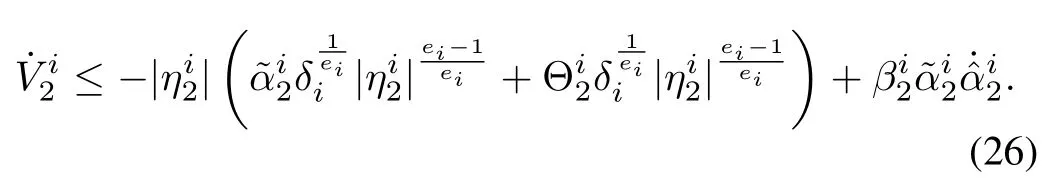
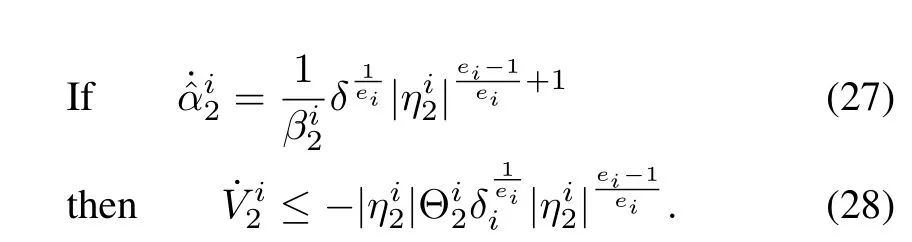
Just as in the previous step,we can prove thatis uniformly continuous,and the finite time convergence of the trajectories to the sliding manifolds can be guaranteed;0.Hence,aftert2,the estimation error stays equal to zero.

Step 3:For the timet2≤t≤tn,the remaining error dynamics becomes

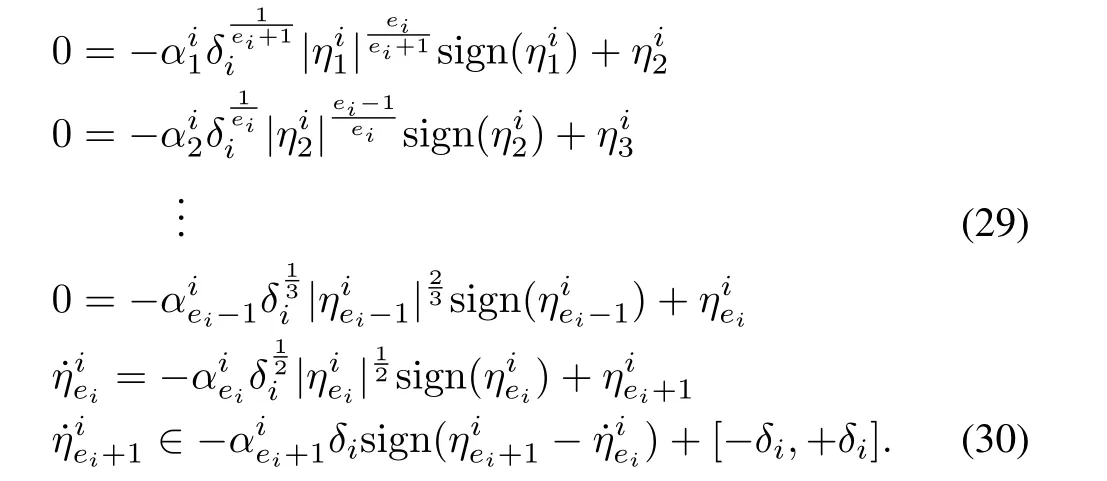
The Lyapunov candidate function can be chosen as

Taking derivative of the Lyapunov function and substituting foras in Step 1 yields,

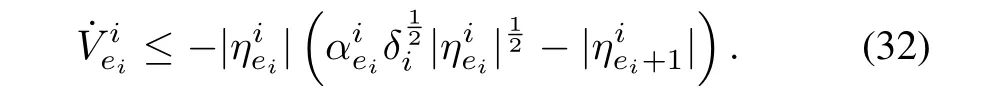
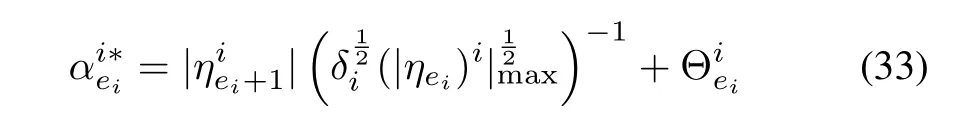
The Lyapunov function can be modified as

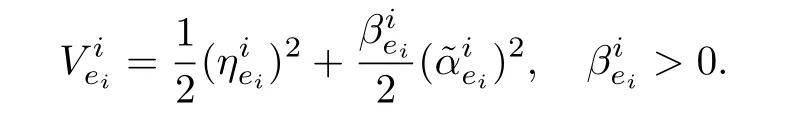
Taking the derivative ofand proceeding in the same way as in Step 1 yields,

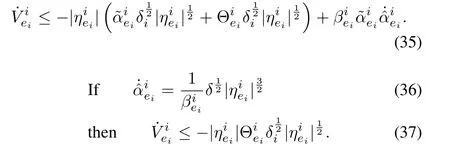
Similar to Step 1,we can findas uniformly continuous,and the finite time convergence of the trajectories to the sliding manifolds can be guaranteed;Hence,aftertei,the estimation error stays equal to zero.

Step 4:For the timethe remaining error dynamics becomes

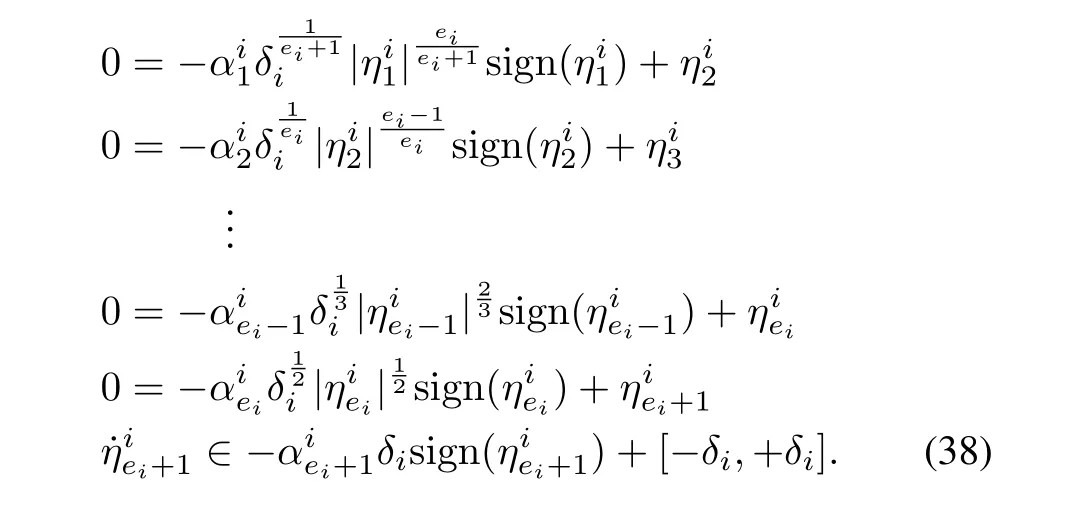
The Lyapunov candidate function can be chosen as

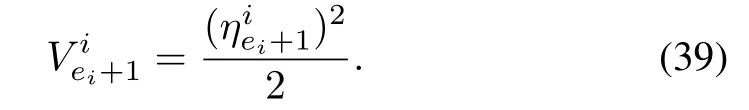
Taking derivative of the Lyapunov function yields

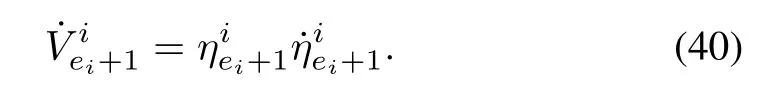
Substituting for

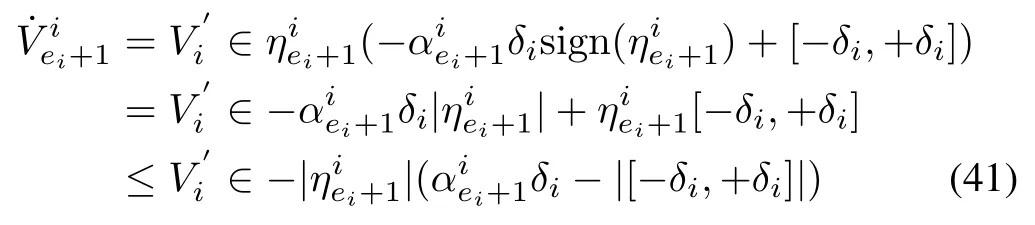
whererepresents the absolute values of the elements of the closed set.The nominal value ofcan be chosen as

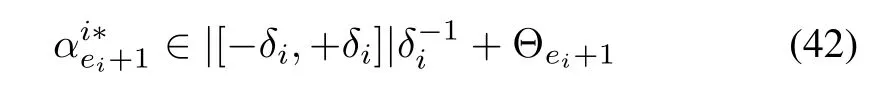
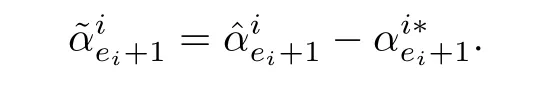
The Lyapunov function can be modified as

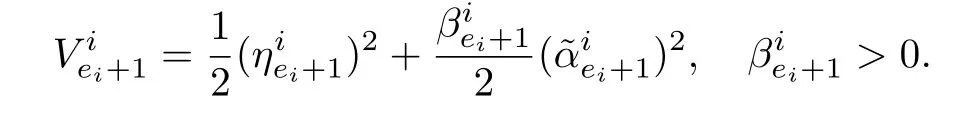
Taking the derivative,

Using(42),

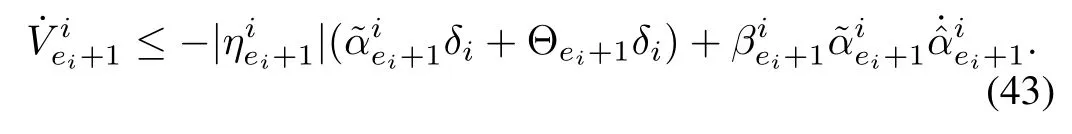
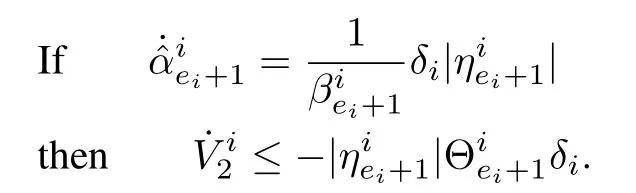
Hence,as in the previous steps,the finite time convergence of the trajectories to the sliding manifolds can be guaranteed.From(41),it is clear thatis a simple and sufficient condition to ensure the same.

Theorem 2:Upon satisfaction of Conditions 1?3,for any nonlinear system,with the transformed motion dynamics given by(2)and(3),and the control input is Lebesgue measurable,the disturbance inputs can be estimated from the observer structure,represented by(4),as

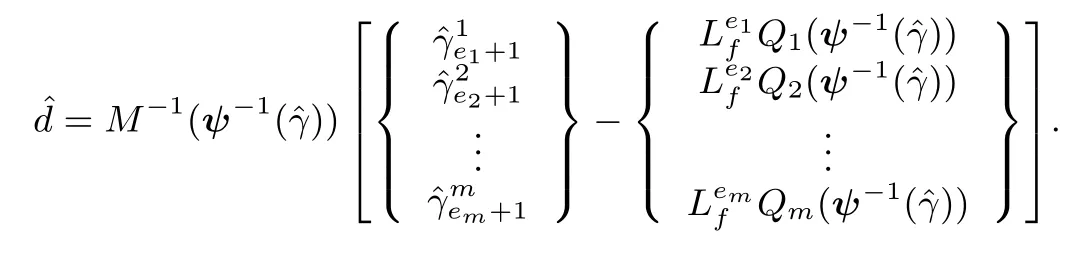
Proof:When,from(11),it is clear thatsinceWhen,hence.Proceeding in this way,the following results can be obtained from(11):

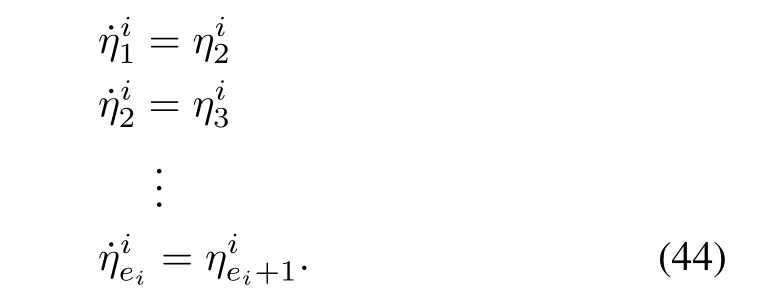
From(10)and(44),.Hence,using(3),the disturbance estimates can be obtained as

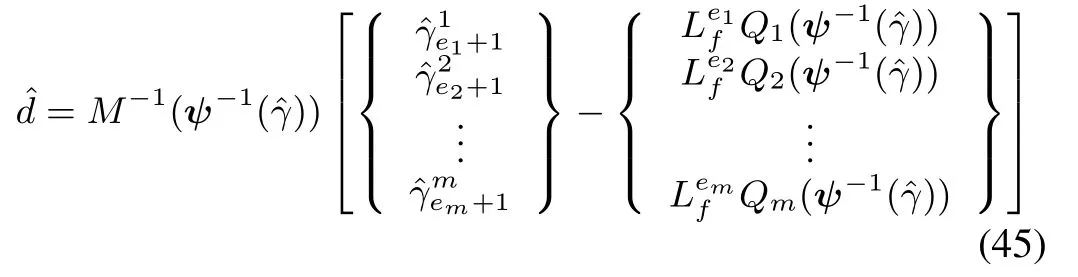
The observer design is repeated with an alternate HOSM differentiator structure as well.

Corollary 1:Upon satisfaction of Conditions 1?3,for any nonlinear system,with the transformed motion dynamics given by(2)and(3),and the control input is Lebesgue measurable,choosing an alternate structure for an HOSM differentiator[19],[24]given by,

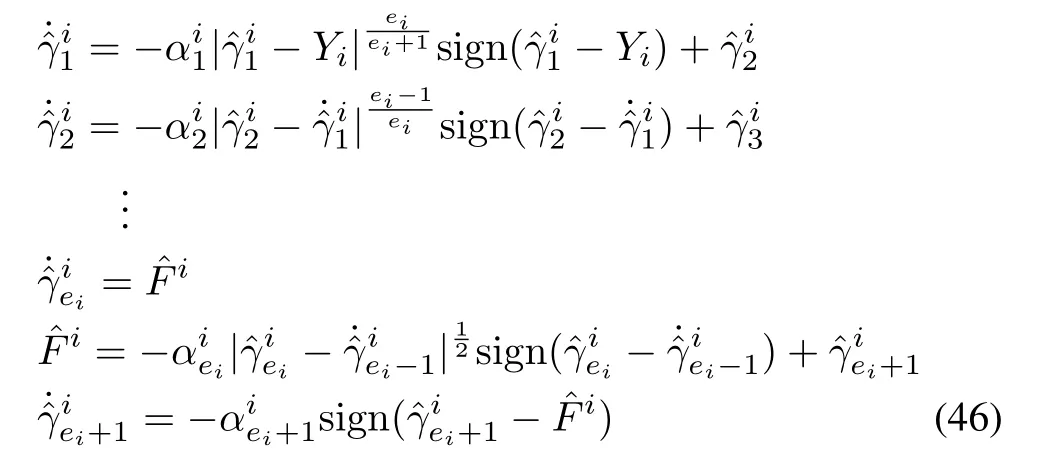
the disturbance inputs can be estimated as

Proof:Unlike Theorems 1 and 2,in this case,F i(t,γ,d)is defined as

The proof will be similar to that of Theorem 2.The update laws for the observer gains also remain the same,provided the value ofδiis to be taken as 1.Finally,as in previous case,we will arrive at the condition,.From this,making use of(48),the required expression for disturbance observer can be obtained.

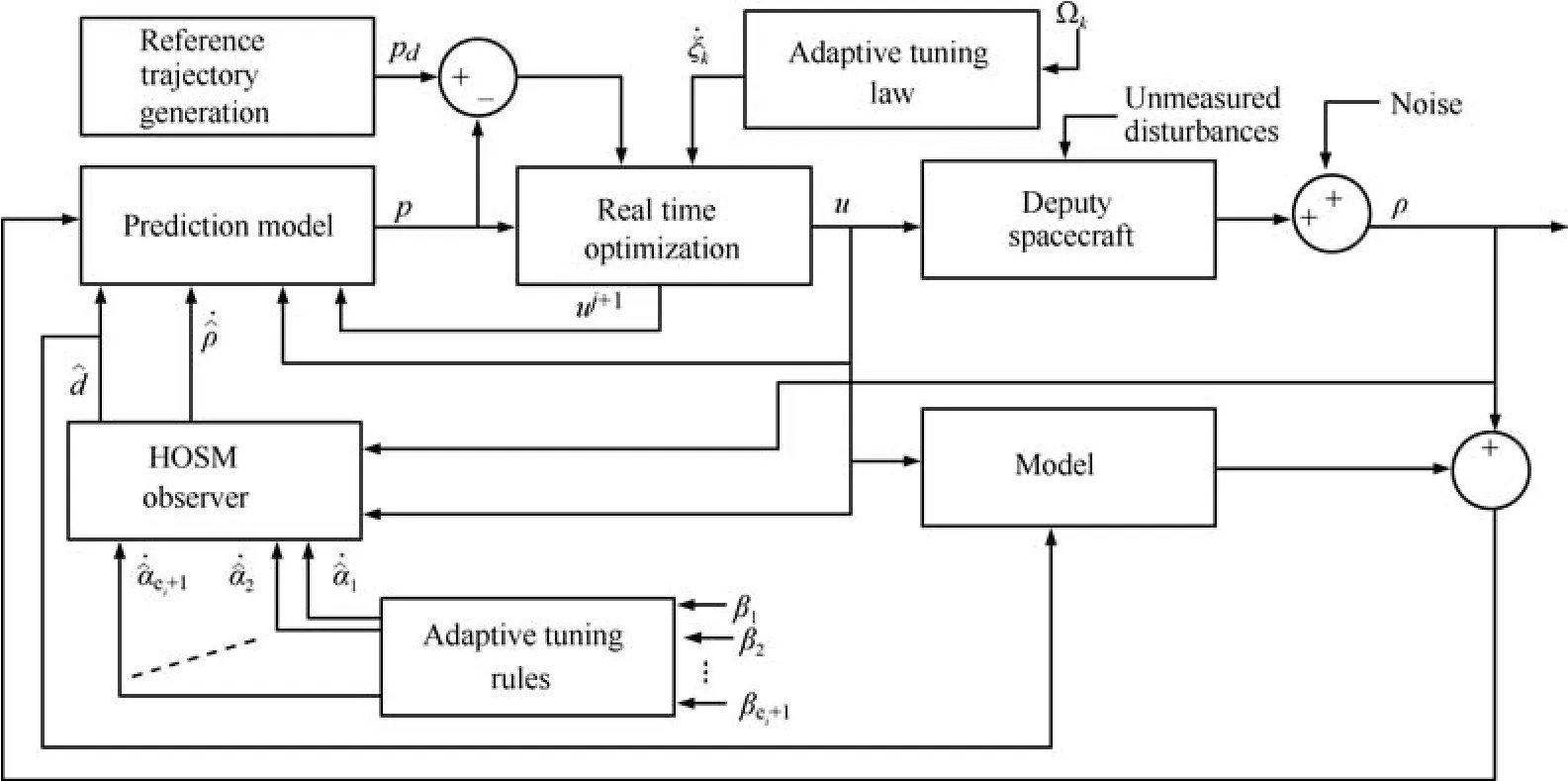
Fig.1.Block schematic of the proposed scheme.

The complete NMPC algorithm,incorporating the disturbance estimates from an HOSM disturbance observer,isgiven in next section.

III.NONLINEAR MODEL PREDICTIVE CONTROL

The block schematic of the proposed scheme is shown in Fig.1.The fundamentals of NMPC problem and the optimization algorithm used[16],[17],can be detailed as follows.The objective is to find the control input sequenceu0,u1,...,uN?1,that minimizes the following nonquadratic cost function:

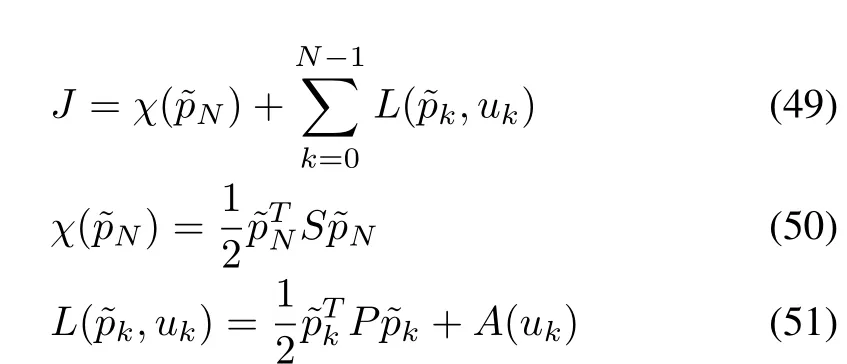
whereA:Rn→R,is utilized to incorporate the control constraints,and it can be defined in terms of continuous one-to-one real-analytic integrable inverse hyperbolic tangent function[27]as

whereumaxis the bound on control input.The discretized dynamic constraints to be satisfied,is given by

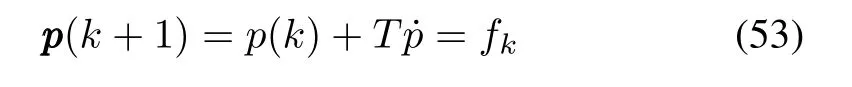
wherefkis a function ofdk,which can be estimated using HOSM disturbance observer;andpdis the reference trajectory.

The Hamiltonian can be written as

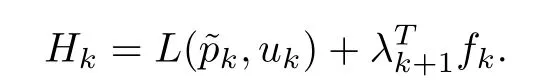
For driving the derivatives of the cost function to zero,the Lagrange multipliers can be chosen as

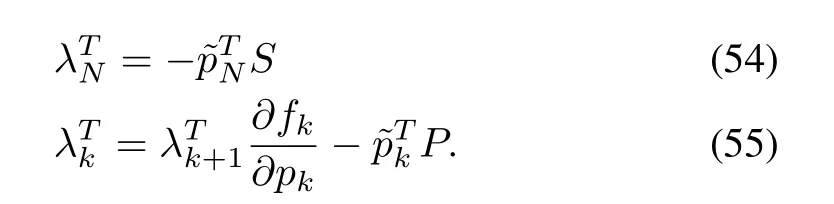
The gradient of the Hamiltonian is given by

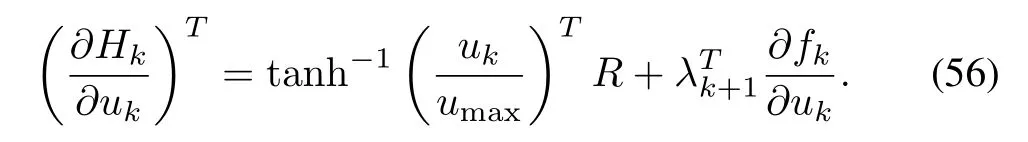
The control update law[16]can be written as

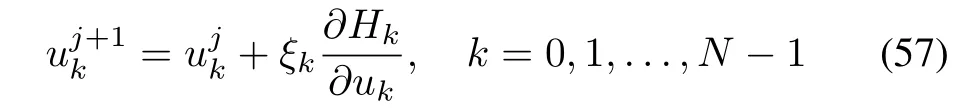
whereξkis the step size.

Theorem 3:For the given nonquadratic cost function,the Hamiltonian can be minimized,and convergence to the optimal value function can be guaranteed,if the step size is updated using the adaptive update law.

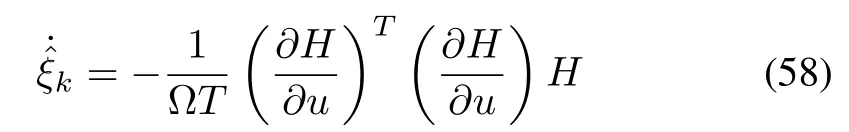
whereTis the sampling time.

Proof:Consider the energy function

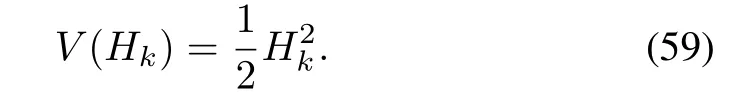
Taking the derivative,

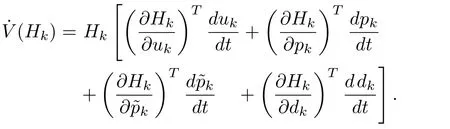
From(57),

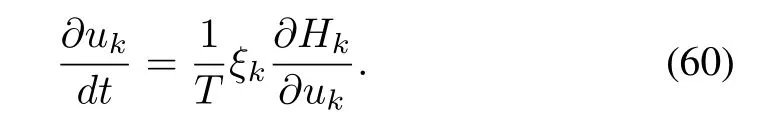
Hence,

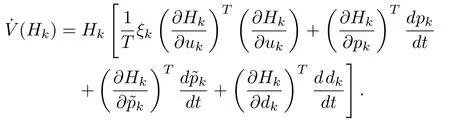
Suppose that,there exists a finite optimal value for step size,at the given operating condition,such that the Hamiltonian can be minimized,and convergence to the optimal value function can be guaranteed.

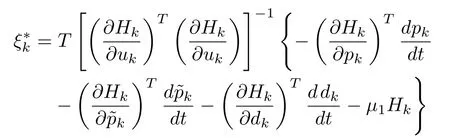
whereμ1＞0.Since the computation ofinvolves the unknown parameters such as derivative of disturbance vector,and the gradient of Hamiltonian with respect to the disturbance vector,it is not possible to computefrom the above equation.Hence we are proposing an adaptive tuning algorithm for updating the step size for the given operating condition.For a given operating condition,the optimal value of step size,should be a fixed value.From the above equation,the optimal value of step size,is assumed to be slow ly varying with respect to time.Hence it is reasonable to assume thatat the given operating condition.The response ofshown in SectionVconfirms this,i.e.,is settling to different fixed values ofat different operating conditions.Ifrepresents the estimated value of the step size,the adaptation error can be defined as

The energy function can be modified as

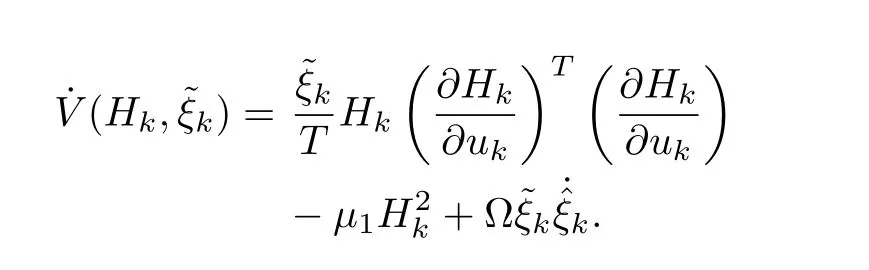
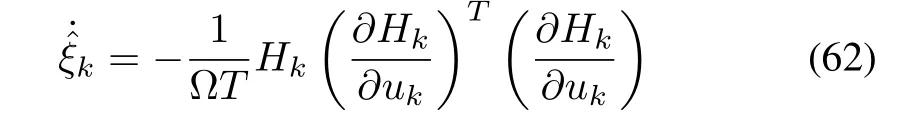
Substituting foryieldsHenceis negative semidefinite,this implies thatHkandare bounded.Taking the derivative of

If the update law is chosen such that

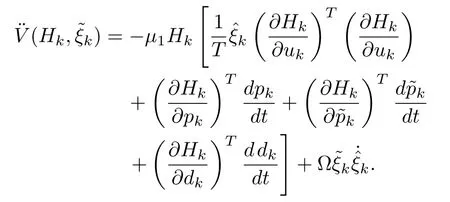
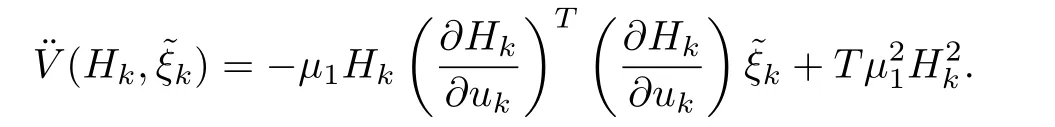
The optimal value of gain,is a bounded value.Sinceis bounded,is also bounded.Sinceuis assumed to be Lebesgue measurable,bounded and Lipschitz,from(60),we can find thatis bounded.Since,we have already proved thatHkis bounded,from the above equation,it is clear thatis bounded.Hence,is uniformly continuous,and by Barbalat’s Lemma[32],it has been found that

The complete NMPC algorithm[16],[17],with the real time finite horizon optimization technique,is provided in the next section.

IV.TRACKING CONTROL OF SFFUSING THE PROPOSED SCHEME

A schematic of the Earth orbiting SFF system in a leader follower based framework is shown in Fig.2.

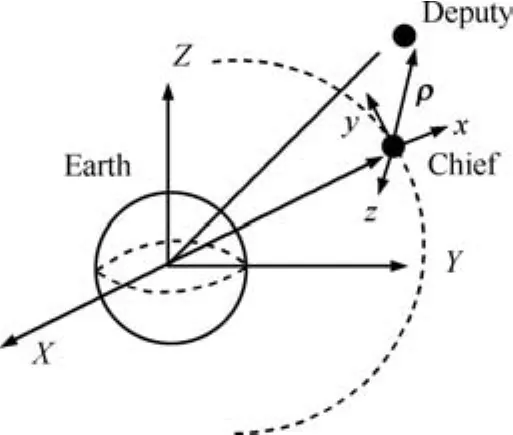
Fig.2.Schematic representation of the satellite formation flying system.

The chief(leader)is assumed to be in circular orbit.The equations of motion of the deputy(follower)spacecraft[2],[36]are defined in local-vertical-local-horizontal(LVLH)frame,fixed at the center of the chief.Letr=[r,0,0]Tdenotes the position vector of the chief in Earth centered inertial reference frame,andρ=[x,y,z]Tdenotes the relative position vector of the deputy with respect to the chief in LVLH frame.The nonlinear SFF model can be written as follows:

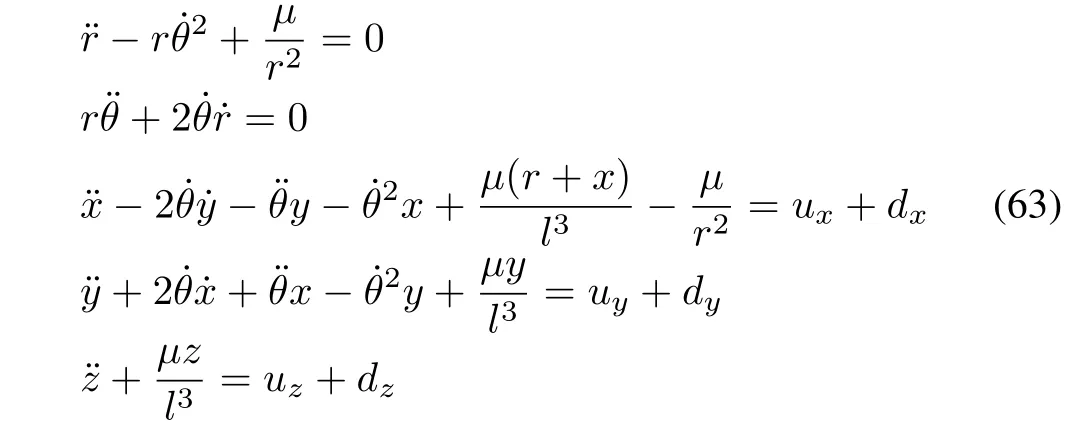
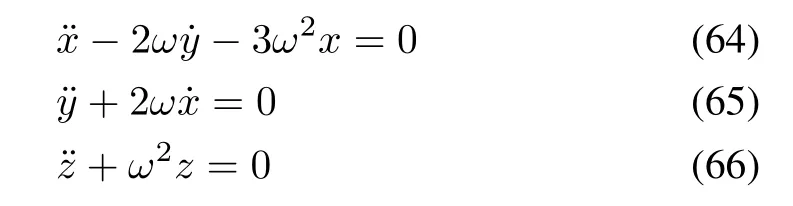
The reference trajectory is chosen such that it satisfies:

wherepdrepresents the desired trajectory.Our objective is to design an optimal control law for controlling the relative positions and velocities of the deputy with respect to chief.It is assumed that deputy has the on board arrangements to acquire the information regarding its relative position with respect to chief.For the system model given by(63),

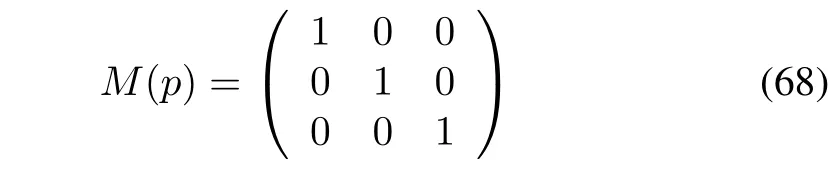
is nonsingular;hence,the relative degree of the system is{2,2,2}.The distribution,Λ=span{w1,w2,w3},is in volutive.Therefore,the system is locally detectable in the domain Υ.The structure of the adaptive gain HOSM can be defined as follows:

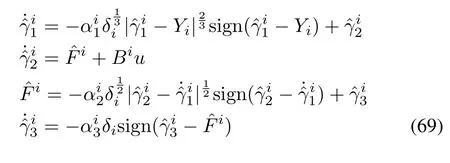
whereY=[x,y,z]T.Using Theorem 2,the disturbance estimates can be obtained as

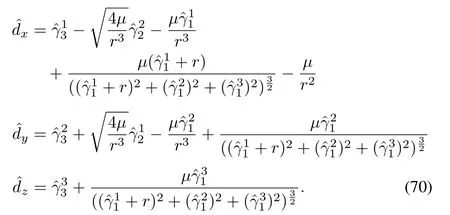
The velocity estimates can be obtained asandThese estimates are utilized by the prediction model in the NMPC.Using the alternate observer structure given by(46),the disturbances can be estimated as follows:

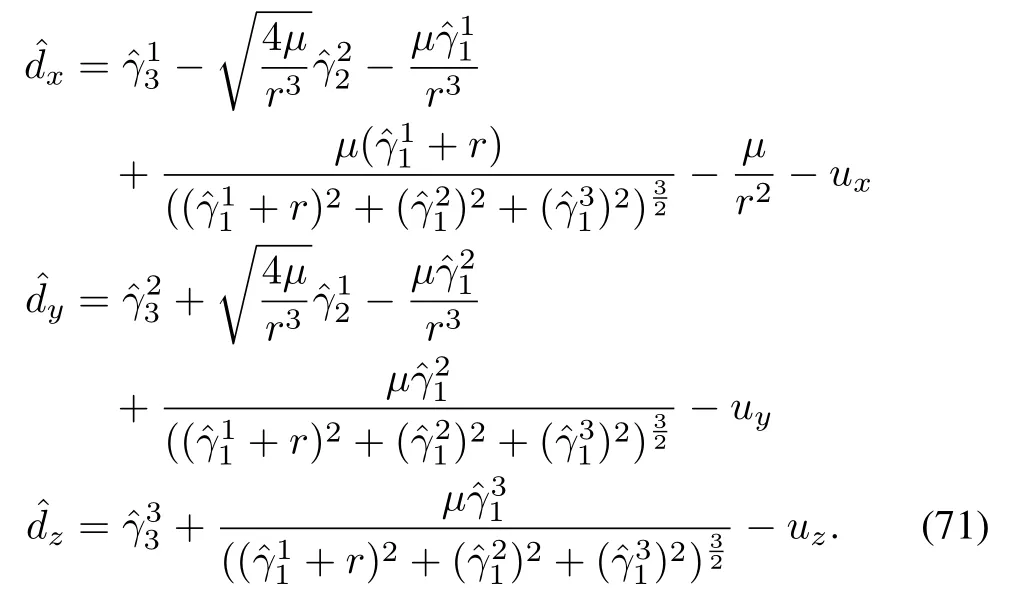
The complete tracking scheme is detailed in Algorithm 1.

The simulation results,given in the next section,confirm the efficacy of the proposed scheme.

V.RESULTS AND DISCUSSION

Random intermediate perturbations are applied,with an initial off set of(ρ?ρd)=[400,400,300]Tm,and[0,0,0]Tm.The Lipschitz constants are chosen asδ1=1.7×10?4,δ2=8×10?4andδ3=6×10?6respectively.The values ofβare chosen asand[6E?3,3E?2,1E?6]Trespectively.The value of ? used in the update law for step size is taken as0.1.The control constraint,is chosen as 80mm/s2,?i,since we have considered avery high initial distance separation of 640.3m,for the desired formation size of 1000m.A ll the observer gains are initialized as zero.The other parameters such asR=(1E?3)I(3),andS=(2E?2)I(6),are chosen heuristically,whereIis identity matrix.The phase portrait given by Fig.3,and the relative position trajectories of the deputy given by Fig.4,confirm the robustness of the proposed approach.A projected circular formation[2]is maintained along they-zplane.Fig.5 shows the applied intermediate disturbances and the reconstructed signal using the proposed HOSM observer.Different types of perturbations have been applied alongx,yandzdirections.The perturbing accelerations are expressed as functions of angular velocity of the circular reference orbit(ω).The HOSM disturbance observer is found to be capable of rebuilding even the worst case disturbances.The estimated relative velocity trajectories,and the corresponding error histories are shown in Figs.6 and 7 respectively.The rotated magnified version of the initial region of tracking result is shown in cubical box.Irrespective of the initial values,the estimated trajectories are found to be converging to the actual one within 100s.To show the convergence speed,the velocity error histories are provided in Fig.8.

Algorithm 1.NMPC algorithm

TABLE I SIMULATION PARAMETERS

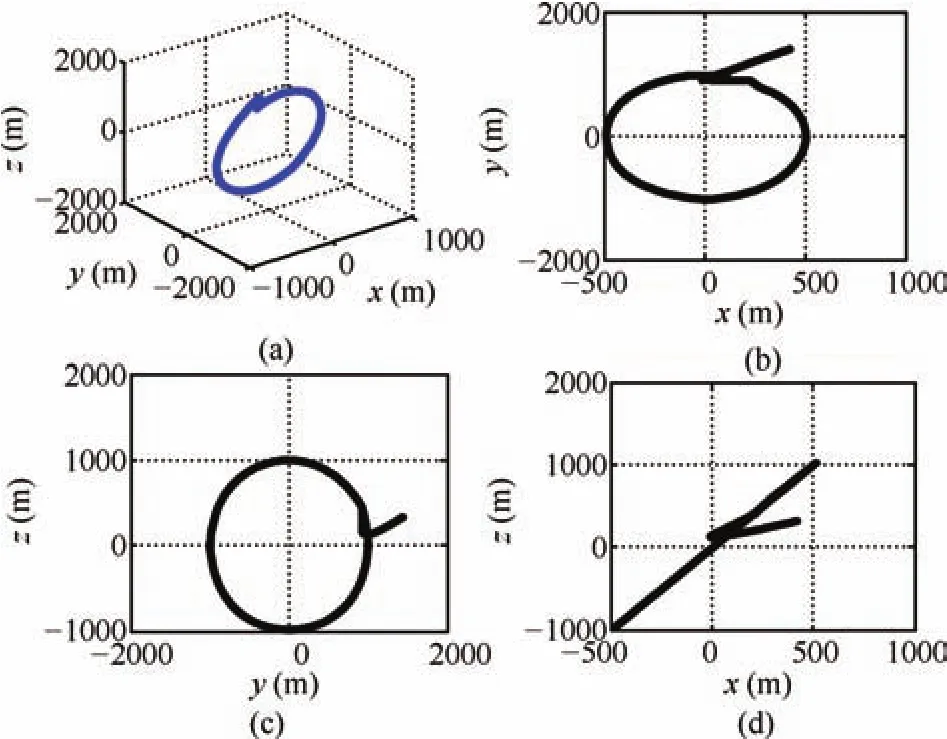
Fig.3.Phase portrait:(a)X-Y-Z coordinates,(b)X-Y coordinates,(c)YZ coordinates and,(d)X-Z coordinates.

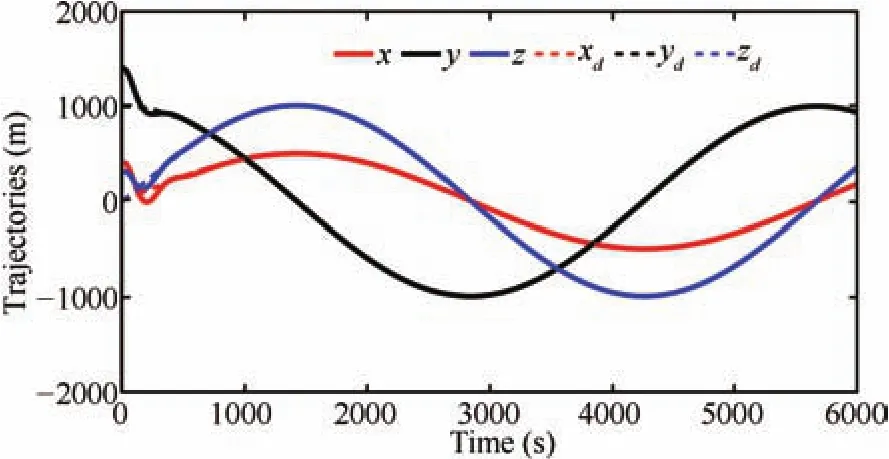
Fig.4.Relative position trajectories of the deputy.

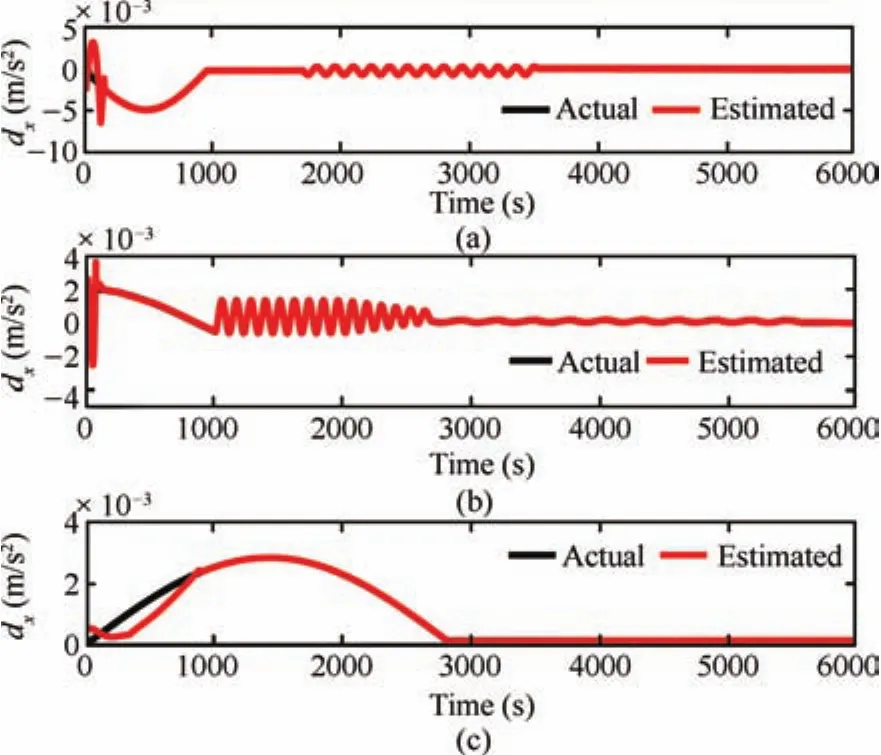
Fig.5.Disturbance trajectories of the deputy.

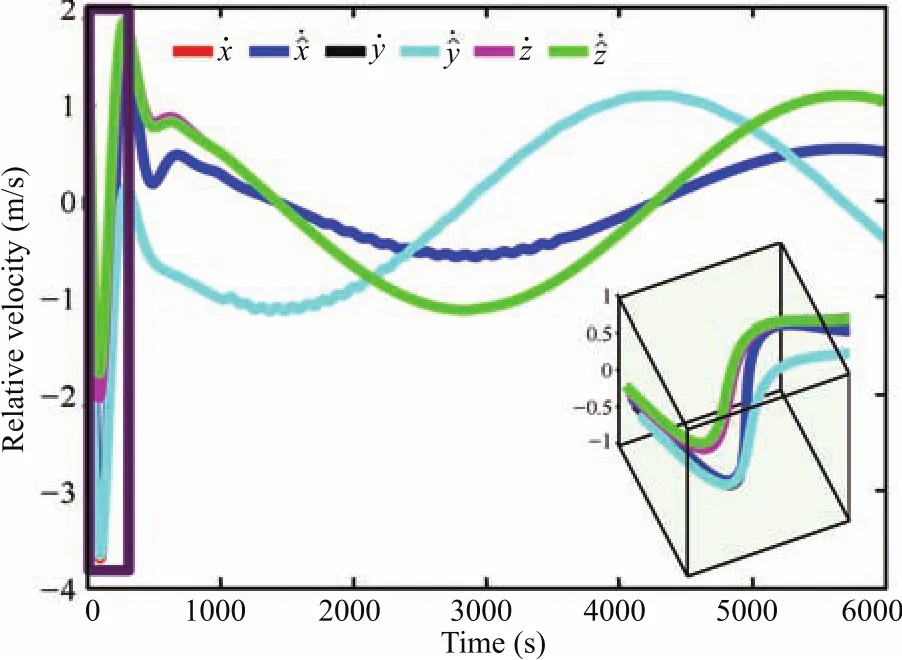
Fig.6.Estimated relative velocity trajectories of the deputy.

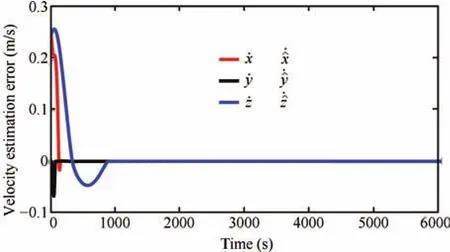
Fig.7.Relative velocity estimation error trajectories of the deputy.

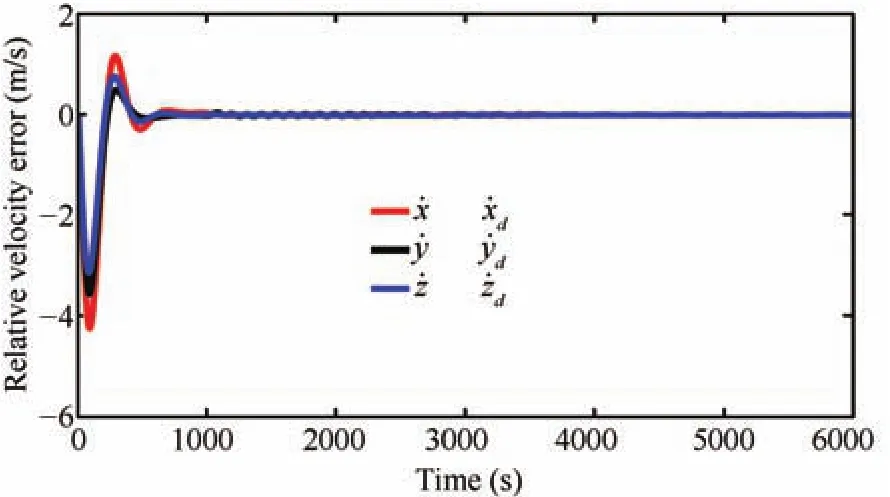
Fig.8.Relative velocity error trajectories of the deputy.

The control histories given by Fig.9,show that the required thrust acceleration inputs are staying within the available control authority.The maximum control effort is found to be less than 60mm/s2,even though the relative position has been perturbed by 64%,when compared to the required formation size.The control accuracy can be further improved by increasing the length of control horizon,but it can affect the computational performance.The computation time is a key factor in determining the performance of an optimal control technique.Fig.10 shows the computation time at each sampling instant,and the average computational effort per sampling instant is found to be less than 0.5ms.Proper choice of∈can also considerably save the computation time.Fig.11(a)provides the cost function trajectory and Fig.11(b)shows the net distance separation error.

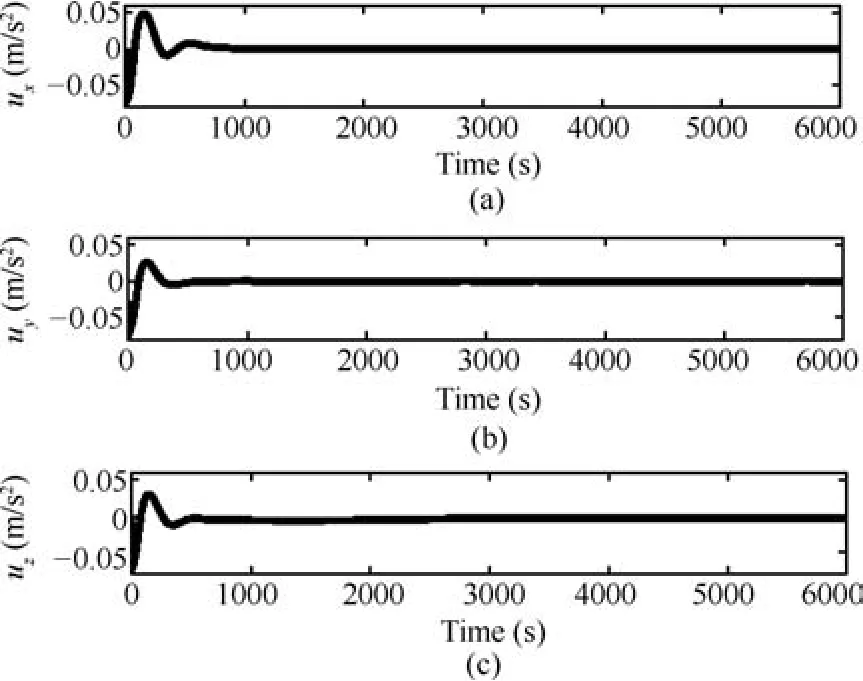
Fig.9.Control inputs to the deputy.

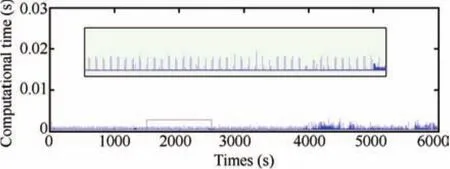
Fig.10.Computation time.

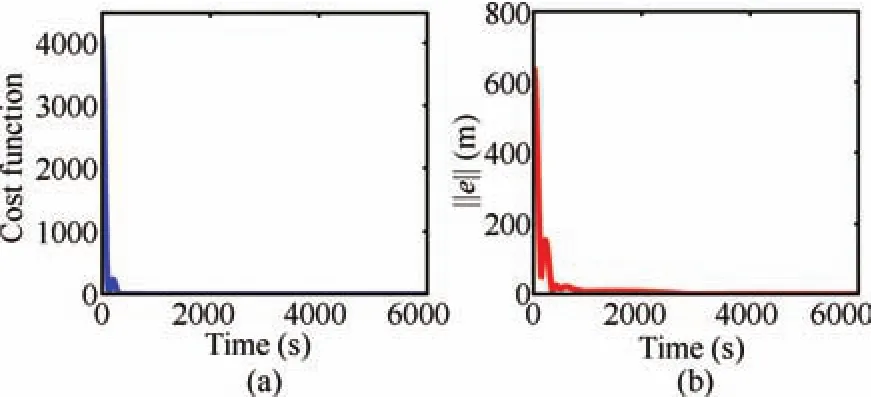
Fig.11.(a)Cost function trajectory and(b)Net relative distance error.

In order to show the tuning drift,the time responses of the various adapted parameters such as observer gains and step size are presented in Fig.12.Fig.13 verifies the input constraint handling capability of the proposed NMPC scheme.The simulations are repeated for different values ofumax,with the same level of initial and intermediate disturbances applied as in the previous case.Even though the trajectories are found to be converging with a reasonable speed in all the cases,comparatively more smooth and fast convergence is observed forumax=70mm/s2.From Fig.14,it is clear that the robustness and convergence speed of proposed adaptive gain HOSM are preserved in all the cases,where different initial estimates are chosen in different cases.The performance of the proposed observer,in case of unexpected state jerks,can be validated using Fig.15.The magnified versions of the respective regions of interest confirm the efficiency of the proposed adaptive observer,in dealing with unpredicted state jerks.In order to show the step size adaptation,simulations are repeated for different initial distance separations,and the corresponding tuning responses are provided in Fig.16.From this,it is clear that a heuristic choice of step size may not be appropriate at all operating conditions.

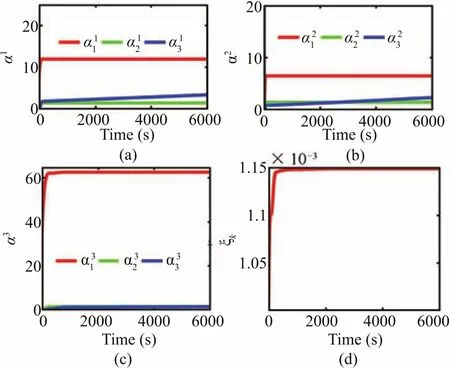
Fig.12. Tuning response:(a)gainα1,(b)gainα2,(c)gainα3 and,(d)step sizeξk.

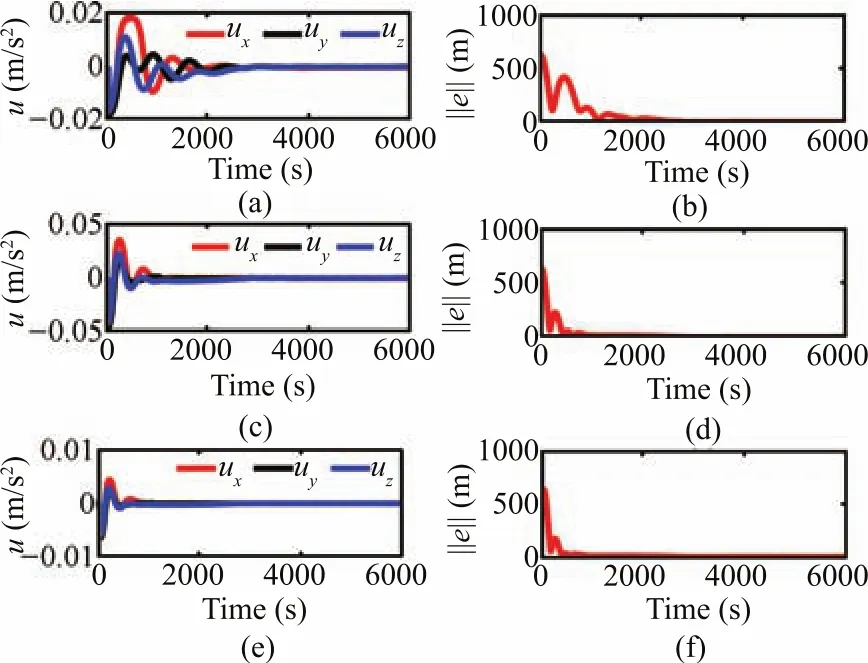
Fig.13. Control histories and net distance separation error for different input constraints(a)and(b)umax=20mm/s2,(c)and(d)umax=50mm/s2,(e)and(f)umax=70mm/s2.

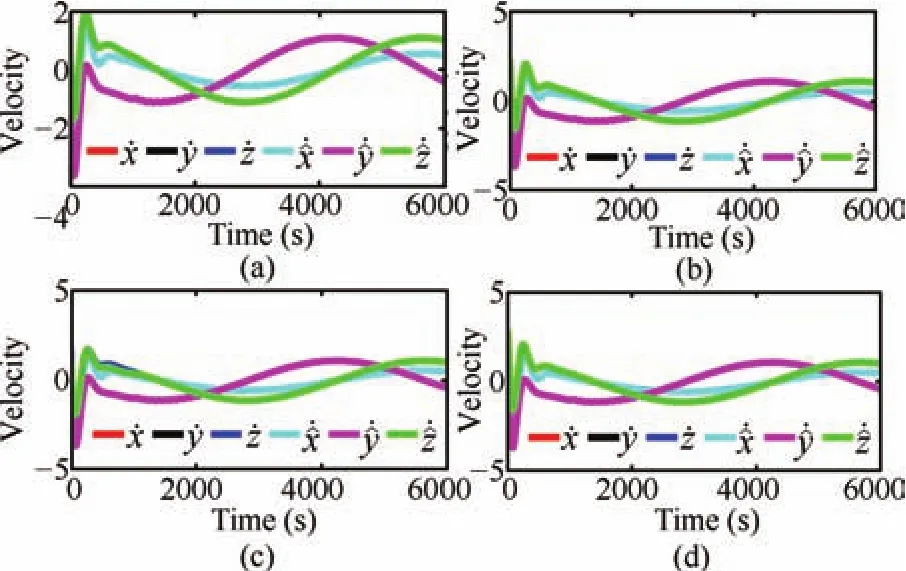
Fig.14. Relative velocity trajectories for different initial estimates.

The estimation responses show that the proposed HOSM will work satisfactorily for locally Lipschitz case as well,provided the Lipschitz nonlinearity is bounded.Fig.17 shows the disturbance estimates obtained using the alternate HOSM observer structure,given by(47).The same levels of random perturbations as in the previous case,have been applied.The results are compared with that of the estimates obtained in Fig.5.The performance of this observer is found to deteriorate,for very high levels of initial perturbations.This reaffirms the efficacy of the proposed observer structure.

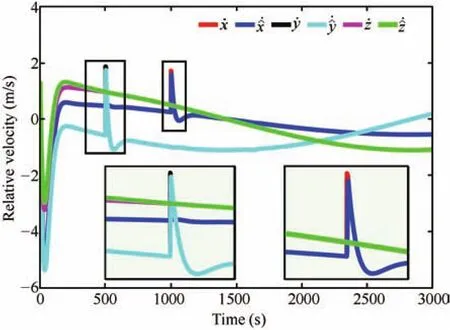
Fig.15.Relative velocity estimation trajectories in the case of induced state jerks.

Fig.16. Tuning response ofξk for different initial conditions.

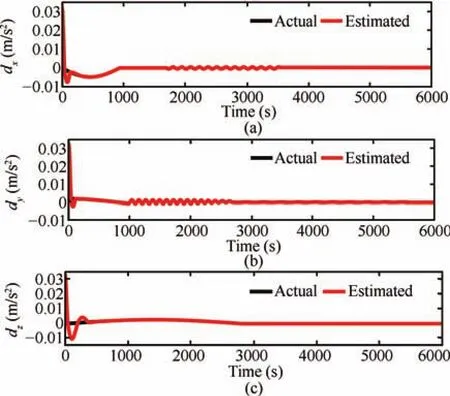
Fig.17. Disturbance trajectories using alternate HOSM differentiator structure.

We have compared the results with that of two recent relevant literature,[26]and[29].In[26],an HOSM based disturbance observer has been used,for improving the disturbance rejection capability of continuous sliding mode controller.There are only slight differences in the differentiator structure,when compared to that of the proposed one.The structure is given by

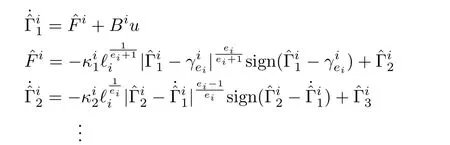
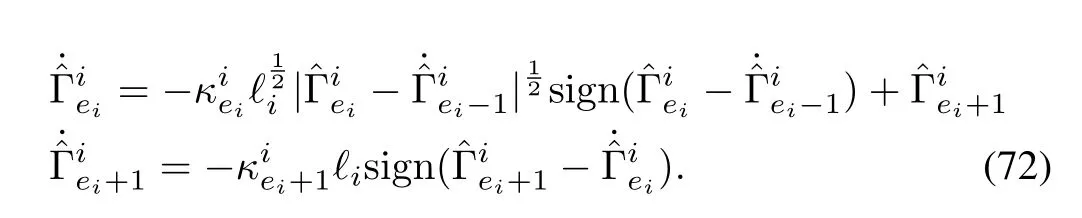
This HOSM based observer,when it is applied to SFF dynamics,utilizes velocity measurements to obtain the disturbance estimates.directly gives the disturbance estimate.We have combined this fixed gain disturbance observer with the proposed NMPC scheme.When the initial estimates are chosen in the neighborhood of the actual value,the results are somewhat satisfactory.But,when those values are perturbed as in the case of previous simulations,the results are not at all satisfactory,and the corresponding trajectories are shown in Fig.18.Since we have retained the same constraint value for the control input,the control requirement remains same.But the speed of convergence is less.

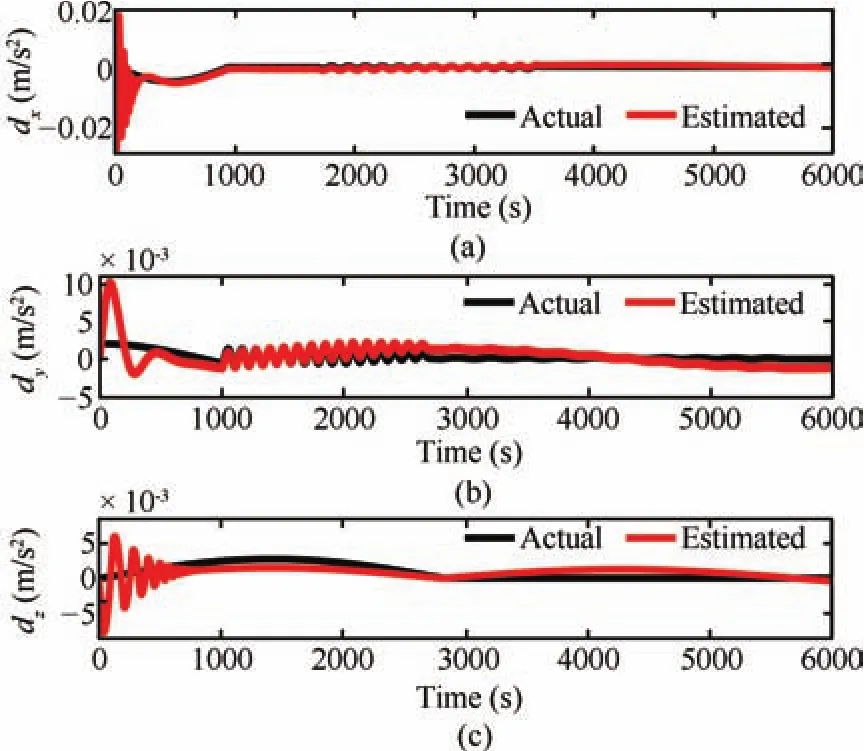
Fig.18. Disturbance estimates with the estimation scheme proposed in[29].

We have also simulated and compared the spacecraft formation flying scheme,which is proposed in[29].In this paper,an HOSM based observer is used for the feed forward compensation of a nonsingular terminal sliding mode controller.The results are given in Figs.19?21.For the ease of design,we can reformulate the dynamics given by(63),in the form,In this case,there is a slight difference in the differentiator structure,when compared to(72),whereInstead of velocity,it uses the tracking error to estimate the unknown disturbances.directly gives the disturbance estimate.The nonsingular terminal sliding surface is chosen asS=ewhereκ=diag{κ1,κ2,...κn};andκi＞0,?i.The control input can be designed aswhereis the disturbance estimate.The observer structure is more or less model dependent.The results show that the control requirement is very high,and the trajectory convergence speed is not even comparable with the proposed scheme.It is found to be more than 3500s.The magnified regions indicate that the disturbance estimation error is also high.

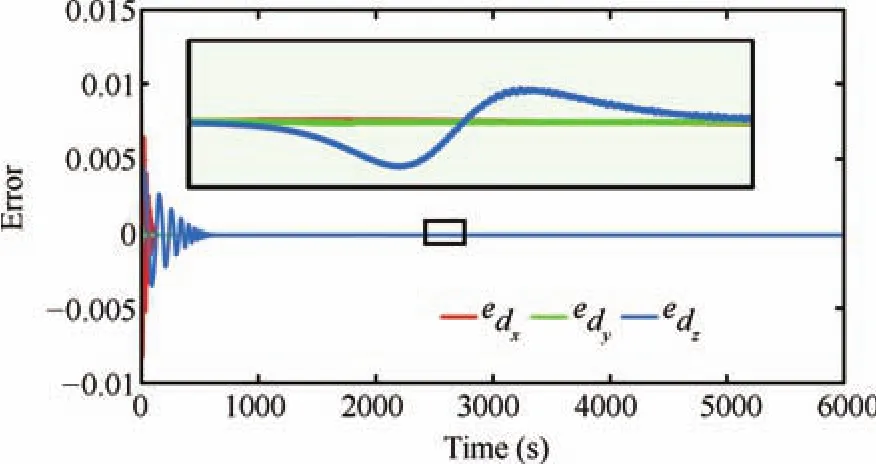
Fig.19.Disturbance estimation error with the estimation scheme proposed in[29].

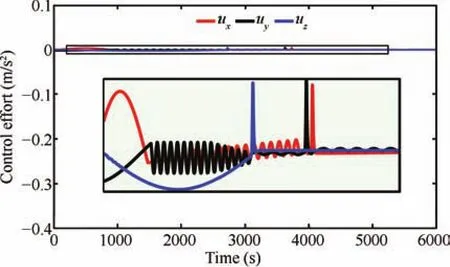
Fig.20. Control inputs with the control scheme proposed in[29].

Fig.21. Relative positions with the control scheme proposed in[29].

From the results,it is clear that,the robustness of the NMPC has been enhanced considerably with the HOSM based disturbance observer.The prescribed structure is found to have good estimation accuracy.The adaptation of the observer gains give enough flexibility in the choice of initial values of estimates.Moreover,it is able to handle unexpected state jerks.The constraint handling has been made easy,and thereby,complexity of the optimization scheme has been reduced,with the choice of nonquadratic cost function,in the NMPC scheme.The adaptation in step size has further improved the efficiency of the optimization algorithm.

V I.CONCLUSION

This paper has focused on the tracking control of spacecraft formation flying system consisting of two LEO satellites,in a leader-follower based framework.In this work,we have applied the HOSM differentiator structure,containing the Lipschitz constant and Lebesgue measurable control input[19],[25],to a complex multi-input multi-output SFF system,to estimate the unmeasurable disturbances and velocities from the noisy position measurements.The observer gains are updated using adaptive tuning algorithms,derived based on Lyapunov stability theory.The prescribed differentiator structure has good estimation accuracy[19].The system is transformed into canonical form using nonlinear coordinate transformation[24].SFF dynamics,having a total vector relative degree equal ton,has been considered.The observer design is repeated with an alternate HOSM differentiator structure as well for comparative study.

A robust NMPC technique with a nonquadratic cost function[27]has been considered for incorporating the control constraints,which has reduced the additional burden of constraint handling in real time optimization algorithms.The heuristic choice of step size in optimization algorithm is not recommendable at all operating conditions.Hence,an adaptive tuning algorithm has been derived for updating the step size.The estimates from the HOSM disturbance observer has been utilized by the output prediction model in NMPC.For simulation studies,the nonlinear SFF model defined in leader fixed Euler-Hill frame,has been considered,and the reference trajectories are generated using Hill-Clohessy-Wiltshire equations of unperturbed motion.Simulation studies are conducted for different levels of perturbations,along with added random measurement noise.The feasibility of the algorithm based on NMPC,combined with the adaptive gain HOSM based disturbance observer and a state estimator,has been evaluated in sufficient detail,and the following conclusions are drawn:

1)The prescribed adaptive gain HOSM differentiator is found to have good estimation accuracy.It fits well as state as well as disturbance estimator for such complex systems like SFF system.

2)The performance of the adaptive gain HOSM is less affected by the extremely high level of initial perturbations applied.

3)The adaptation in observer gain has added more flexibility to the choice of initial estimates.Moreover,the observer is found to be robust to unexpected state jerks.

4)The results indicate that the proposed scheme will work satisfactorily for locally Lipschitz systems with bounded Lipschitz nonlinearity as well.

5)NMPC technique,with the real time open loop finite horizon optimization algorithm is found to be computationally efficient and is best suited for satellite formation control applications.

6)The non-quadratic performance functional has considerably reduced the burden of input constraint handling.

7)The adaptation in step size,is found to be an attractive alternative to the heuristic choice of it,well suited for systems with diverse operating conditions,which may also improve the convergence speed.

8)The inclusion of disturbance estimate in the model prediction is found to add more robustness to the scheme,therefore,eliminates the necessity of exact modeling.

The inclusion of actuator dynamics,can be viewed as a further extension of this work.

[1]D.P.Scharf,F.Y.Hadaegh,and S.R.Ploen,“A survey of spacecraft formation flying guidance and control.Part II:control,”inProc.2004 American Control Conf.,Boston,Massachusetts,2004,pp.2976?2985.

[2]X.Liu and K.D.Kumar,“Network-based tracking control of spacecraft formation flying with communication delays,”IEEE Trans.Aerosp.Electronic Syst.,vol.48,no.3,pp.2302?2314,Jul.2012.

[3]L.Hui and J.F.Li,“Terminal sliding mode control for spacecraft formation flying,”IEEE Trans.Aerosp.Electronic Syst.vol.45,no.3,pp.835?846,Jul.2009.

[4]R.R.Nair and L.Behera,“Swarm aggregation using artificial potential field and fuzzy sliding mode control with adaptive tuning technique,”inProc.2012 American Control Conf.,Montreal,Canada,2012,pp.6184?6189.

[5]T.E.Massey and Y.B.Shtessel,“Continuous traditional and high order sliding modes for satellite formation control,”J.Guid.Control Dynamics,vol.28,no.4,pp.826?831,Jul?Aug.2005.

[6]R.R.Nair,L.Behera,V.Kumar,and M.Jamshidi,“Multisatellite formation control for remote sensing applications using artificial potential field and adaptive fuzzy sliding mode control,”IEEE Syst.J.,vol.9,no.2,pp.508?518,Jun.2015.

[7]M.S.de Queiroz,V.Kapila,and Q.G.Yan,“Adaptivenonlinear control of multiple spacecraft formation flying,”J.Guid.Control Dynamics,vol.23,no.3,pp.385?390,May 2000.

[8]X.W.Dong,B.C.Yu,Z.Y.Shi,and Y.S.Zhong,“Time-varying formation control for unmanned aerial vehicles:theories and applications,”IEEE Trans.Control Syst.Technol.,vol.23,no.1,pp.340?348,Jan.2015.

[9]X.W.Dong,Y.Zhou,Z.Ren,and Y.S.Zhong,“Time-varying formation control for unmanned aerial vehicles with switching interaction topologies,”Control Eng.Pract.,vol.46,pp.26?36,Jan.2016.

[10]L.Ma,H.B.M in,S.C.Wang,Y.Liu,and S.Y.Liao,“An overview of research in distributed attitude coordination control,”IEEE/CAA J.of Autom.Sinica,vol.2,no.2,pp.121?133,Apr.2015.

[11]Y.Ulybyshev,“Long-term formation keeping of satellite constellation using linear-quadratic controller,”J.Guid.Control Dynamics,vol.21,no.1,pp.109?115,Jan.?Feb.1998.

[12]S.B.McCamish,M.Romano,and X.P.Yun,“Autonomous distributed control of simultaneous multiple spacecraft proximity maneuvers,”IEEE Trans.Automat.Sci.Eng.,vol.7,no.3,pp.630?644,Jul.2010.

[13]E.Camponogara and H.F.Scherer,“Distributed optimization for model predictive control of linear dynamic networks with control-input and output constraints,”IEEE Trans.Automat.Sci.Eng.,vol.8,no.1,pp.233?242,Jan.2011.

[14]X.H.Xia and J.F.Zhang,“Operation efficiency optimisation modelling and application of model predictive control,”IEEE/CAA J.of Autom.Sinica,vol.2,no.2,pp.166?172,Apr.2015.

[15]L.Breger,J.P.How,and A.Richards,“Model predictive control of spacecraft formations with sensing noise,”inProc.2005 American Control Conf.,Portland,OR,USA,2005,pp.2385?2390.

[16]G.J.Sutton and R.R.Bitmead,“Performance and computational implementation of nonlinear model predictive control on a submarine,”inNonlinear Model Predictive Control,F.Allg?ower and A.Zheng,Eds.,Birkh?user Basel,2000,pp.461?471.

[17]J.Shin and H.J.Kim, “Nonlinear model predictive formation flight,”IEEE Trans.Syst.Man Cybernet.-A:Syst.Humans,vol.39,no.5,pp.1116?1125,Sep.2009.

[18]K.R.Muske and T.A.Badgwell,“Disturbance modeling for offset-free linear model predictive control,”J.Process Control,vol.12,no.5,pp.617?632,Aug.2002.

[19]A.Levant,“Higher-order sliding modes,differentiation and output feedback control,”Int.J.Control,vol.76,no.9?10,pp.924?941,Sept.2003.

[20]A.Benallegue,A.Mokhtari,and L.Fridman,“High-order sliding-mode observer for a quadrotor UAV,”Int.J.Robust Nonlin.Control,vol.18,no.4?5,pp.427?440,Mar.2008.

[21]A.Levant, “Robust exact differentiation via sliding mode technique,”Automatica,vol.34,no.3,pp.379?384,Mar.1998.

[22]R.Sharma and M.Aldeen,“Fault and disturbance reconstruction in non-linear systems using a network of interconnected sliding mode observers,”IET Control Theory Appl.,vol.5,no.6,pp.751?763,Apr.2011.

[23]P.P.Menon and C.Edwards,“An observer based distributed controller for formation flying of satellites,”inProc.2011 American Control Conf.,San Francisco,CA,USA,2011,pp.196?201.

[24]L.Fridman,Y.Shtessel,C.Edwards,and X.-G.Yan,“Higher-order sliding-mode observer for state estimation and input reconstruction in nonlinear systems,”Int.J.Robust Nonlin.Control,vol.18,no.4?5,pp.399?412,Mar.2008.

[25]S.Iqbal,C.Edwards,and A.I.Bhatti,“Robust feedback linearization using higher order sliding mode observer,”inProc.50th IEEE Conf.Decision and Control and European Control Conf.(CDC-ECC),Orlando,FL,USA,2011,pp.7968?7973.

[26]C.X.Mu,Q.Zong,B.L.Tian,and W.Xu,“Continuous sliding mode controller with disturbance observer for hypersonic vehicles,”IEEE/CAA J.of Autom.Sinica,vol.2,no.1,pp.45?55,Jan.2015.

[27]A.Heydari and S.N.Balakrishnan,“Finite-horizon control-constrained nonlinear optimal control using single network adaptive critics,”IEEE Trans.Neural Netw.Learning Syst.,vol.24,no.1,pp.145?157,Jan.2013.

[28]N.Boizot,E.Busvelle,and J.-P.Gauthier,“An adaptive high-gain observer for nonlinear systems,”Automatica,vol.46,no.9,pp.1483?1488,Sep.2010.

[29]Q.X.Lan,J.Yang,S.H.Li,and H.B.Sun,“Finite-time control for 6d of spacecraft formation flying systems,”J.Aerosp.Eng.,vol.28,no.5,Article no.04014137,Sep.2015.

[30]A.Isidori,Nonlinear Control Systems(Third edition).Springer:Berlin,1995.

[31]A.F.Filippov,Differential Equations with Discontinuous Righth and Sides.Dordrecht:Kluwer Academic,1988.

[32]J.-J.Slotine and W.P.Li,Applied Nonlinear Control.Englewood Cliffs,NJ:Prentice-Hall,1991.

[33]S.P.Bhat and D.S.Bernstein,“Geometric homogeneity with applications to finite-time stability,”Math.Control Signals Syst.,vol.17,no.2,pp.101?127,Jun.2005.

[34]A.Levant,“Homogeneity approach to high-order sliding mode design,”Automatica,vol.41,no.5,pp.823?830,May 2005.

[35]Y.Orlov,“Finite time stability and robust control synthesis of uncertain switched systems,”SIAM J.Control Optim.,vol.43,no.4,pp.1253?1271,Apr.2004.

[36]K.T.Alfriend,S.R.Vadali,P.Gurfil,J.P.How,and L.S.Breger,Spacecraft Formation Flying:Dynamics,Control and Navigation.Amsterdam:Elsevier,2010.

[37]D.Vallado,Fundamentals of Astrodynamics and Applications(Second edition).New York:Springer,2001.