Suboptimal Robust Stabilization of Discrete-time Mismatched Nonlinear System

Niladri Sekhar Tripathy,Indra Narayan Kar,,and Kolin Paul,

I.INTRODUCTION

REQUIREMENT of exact system model to design a feedback control law is the primary shortcoming of the classical feedback control technique.An uncertain system model is a more realistic representation and has far greater significance over the exact system model.However,there are open problems of designing a control law to deal with system uncertainties.To deal with parametric uncertainty,F.Lin and D.Wanget al.have proposed a continuous-time robust control technique for both linear and nonlinear system[1]?[5].In both the cases,they have formulated an equivalent optimal control problem to derive the proposed robust control input.The optimal control problem is solved based on the nominal dynamics by minimizing a quadratic cost-functional with the know ledge of uncertainty bound.Similar concepts are used for nonlinear continuous system in[6],[7],where a non-quadratic cost-functional is considered.The discrete-time version ofthe proposed robust-optimal control approach is still an open problem.Recently,Wanget al.[8]have extended the Lin’s approach[1]?[3]for a discrete-time nonlinear system.To realize the robust control law,the assumption in their work is that the physical system is affected by matched uncertainty(i.e.,uncertainty is in the range space of input matrix[9]?[11]).But there are several physical systems like maglev suspension system[12],[13],aircraft engine system[14],the movement control of truck-trailer problem[15],where the so-called matching condition does not hold.Therefore considering mismatched uncertainty in both state and input functions is a more realistic control problem.In general,it is known that the existence of stabilizing control law can be guaranteed for matched uncertainty but not so form is matched system.

In this paper,a discrete-time robust control technique for uncertain nonlinear system is proposed.The system is primarily affected by mismatched uncertainty due to bounded parametric variation.To stabilize such systems,a robust control law is derived by solving a nonlinear optimal control problem for nominal virtual system with a cost-functional.To solve the nonlinear optimal control problem,the solution of a discretetime general Hamilton-Jacobi-Bellman (DT-GHJB) equation is approximated using a neural network implementation.Based on the approximated solution of DT-GHJB,the cost-functional and control inputs are estimated.The block diagram representation of proposed control approach is shown in Fig.1.

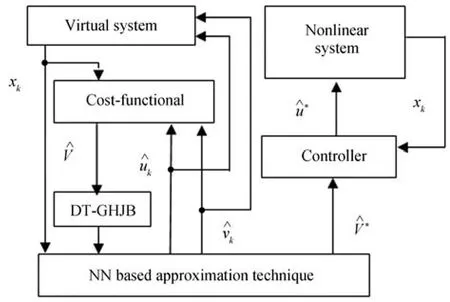
Fig.1.The block diagram of proposed discrete-time robust control technique is shown in this figure.Here notations and represent the system’s state and two estimated control inputs,respectively.Using NN based approximation technique,the estimated cost-functional converges to its optimal costUsingthe optimal inputsandare computed.Inputis applied to the nonlinear uncertain system to solve the robust control problem.

Mathematical analysis is done to prove the stability of the uncertain system by applying the approximated suboptimal control inputs.Finally,numerical results are reported to prove the efficacy of the proposed control algorithm.The key contributions of this work are:

1)A robust control algorithm is proposed for a discrete time nonlinear system with mismatched uncertainty.A robust control law is derived by formulating an equivalent optimal control problem for a nominal virtual system with a quadratic cost-functional.The virtual dynamics have two control inputsuandv.The concept of virtual inputvis used to derive the existence of stabilizing control inputu.The virtual inputvhelps to tackle the mismatched uncertainty.The proposed robust control law ensures asymptotic convergence of uncertain closed-loop system.

2)An optimal solution of a DT-GHJB equation is approximated through a NN implementation,to solve the nonlinear optimal control problem.The approximated inputs ensure the asymptotic convergence of uncertain states both analytically and numerically.The convergence of both the NN weight and cost-functional are also shown through the simulation results.

3)This paper also shows that some of the existing results[8]of matched system are special cases of the proposed results.

Notation&Definitions:The symbol‖x‖denotes the Euclidean norm of a vectorx∈Rn.The Rnrepresents thendimensional Euclidean real space and Rn×mis a set of all(n×m)real matrices.The notationsandX Tdenote the negative definiteness,inverse and transpose of matrixX,respectively.TheIis used to represent an identity matrix.The minimum and maximum eigenvalue of symmetric matrixP∈Rn×nare represented by the notationsλmax(P)andλmin(P),respectively.The number of iteration for discrete-time system is represented byk.Thekthinstant state and control input for a discrete-time system are denoted byxkanduk.A set ? is used to denote a continuous Lipschitz compact set where statexk(including the initial points)satisfy the conditionxk∈?[16].To prove the theoretical results,following definition is used in this paper.

Definition 1[17],[18]:Consider a nonlinear discrete-time system as

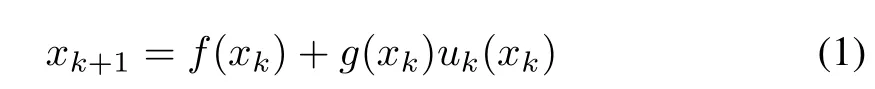
wherexk∈Rnanduk∈Rmare system state and input vector respectively.The functionsf(xk)andg(xk)are continuous nonlinear functions andf(xk)+g(xk)uk(xk)is Lipschitz continuous on a set ? including the origin.The control inputuk(xk)ensures the asymptotic convergence of closed loop system(1),?xk∈?.Let ?uis a set of admissible control inputs and inputukminimizes the cost-functional

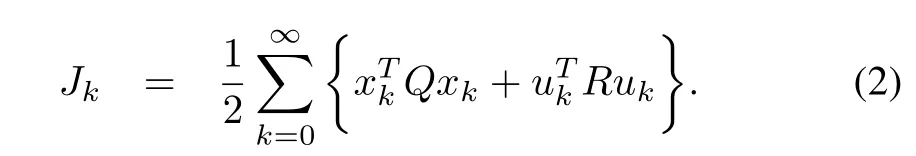
Then,the control inputukis considered as an admissible(i.e.,uk∈?u)with-respect to its state penalty functionand control energy penalty functionuTk Ruk,?xk∈?,if the following conditions hold:

1)?xk∈?,inputuk(xk)is continuous;

2)uk(0)=0;

3)ukmust stabilizes(1)for?xk∈?;

II.ROBUST CONTROL DESIGN

System Description:A discrete-time uncertain nonlinear system is described by the state equation in the form

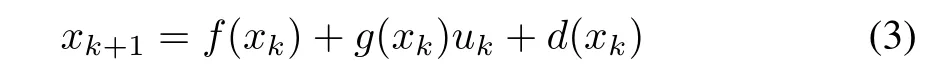
wherexk∈Rnis the state anduk∈Rmis the periodic control input andf∈Rn,g∈Rn×mare the nonlinear functions.It is assumed that(3)is Lipschitz continuous on a compact set ?∈Rnand origin is the equilibrium point,i.e.,f(0)=0 andg(0)=0.The unknown functiond(xk)∈Rnis used to represent the system uncertainty and it is always upper bounded by a known functiondmax(xk),that is

Generally system uncertainties are classified as matched and mismatched uncertainty and they are defined as follows[3],[8]?[10].

Definition 2:System(3)suffers through the matched uncertainty if the uncertaintyd(xk)satisfy the following

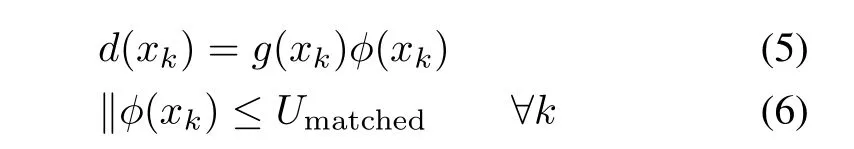
whereφ(xk)is the unknown function andUmatchedis the upper bound of‖φ(xk)‖.In other words,d(xk)is in the range space ofg(xk).

Definition 3:System(3)has mismatched uncertainty if the uncertain componentd(xk)is not in the range space of input matrixg(xk).

For the simplification,uncertainty can be decomposed in matched and m ismatched component as follows

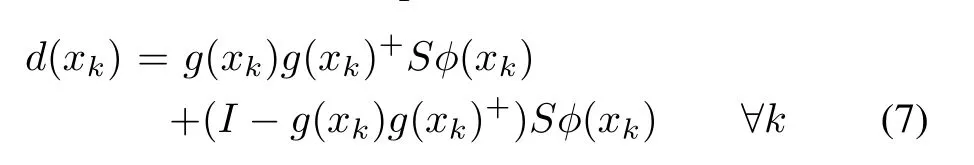
whereandare the matched and mismatched components respectively.The matrixg(xk)+=(gT(xk)g(xk))?1g(xk)Tdenotes the left pseudo inverse of matrixg(xk)[19]andSis a scaling matrix whereS/=g(xk).For a matrixS=g(xk),the uncertainty(7)reduces to a matched one as defined in(5).The decomposition of uncertainty into a matched and mismatched components will be used to define a nominal virtual system for(3)which is discussed in the subsequent subsection.

Problem Statement:Design a state feedback control lawuk=K(xk),to stabilize the discrete-time uncertain nonlinear system(3),such that the closed-loop system is asymptotically stable in the presence of uncertainty(7).

Proposed Solution:This problem is solved in two steps.First,the controller is designed by adopting nonlinear optimal control theory and then an algorithm is used to approximate the solution of DT-GHJB equation.The approximate solution of DT-GHJB equation is used to compute the stabilizing and virtual control inputsukandvk,respectively.

Robust Control Problem:Design a state feedback control lawuk=K(xk)such that the uncertain closed-loop system(3)is asymptotically stable? ‖d(xk)‖≤dmax(xk).In order to stabilize(3),the robust control lawukis designed using an optimal control approach.

Optimal Control Approach:The key idea is to design a discrete-time nonlinear optimal control law for virtual nominal system by minimizing a cost-functionalJ,which depends on the upper-bound of system uncertainty.An extra term(I?g(xk)g(xk)+)Sv(k)is added with the nominal dynamics of(3)to define a virtual system(8).The derived optimal input for virtual system is shown to be a robust input for original uncertain system.The virtual nominal dynamics and cost-functional for solving robust control problem are given below:

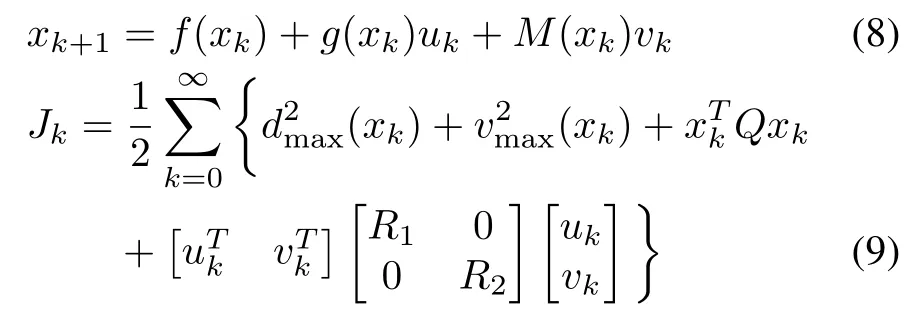
where matricesandR2＞0.Herevmaxis a scalar.

Inspired by the results reported in[20]and[21],the discrete-time HJB(DT-HJB)equation for(8)with the optimal cost-functionalof(9)is

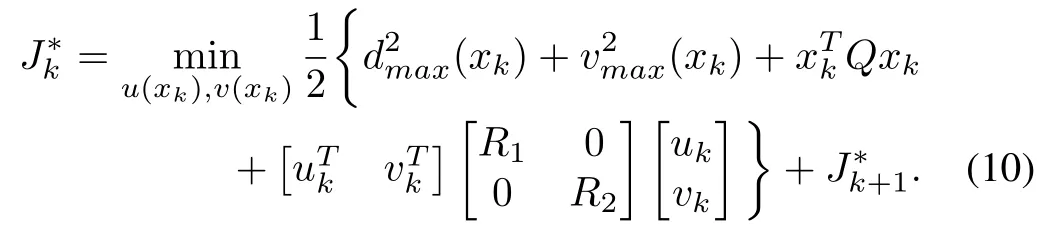
Using(10),the optimal control input for(8)is

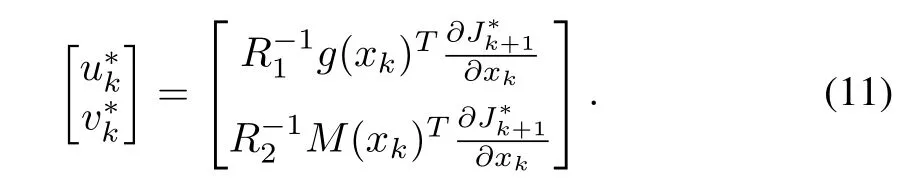
LetV(xk)be a positive definite continuously differentiable function,which satisfiesV(x0)=J(x0,u).Applying Taylor series expansion of the cost-functional,the DT-HJB(10)reduces to discrete-time general HJB as in[21]

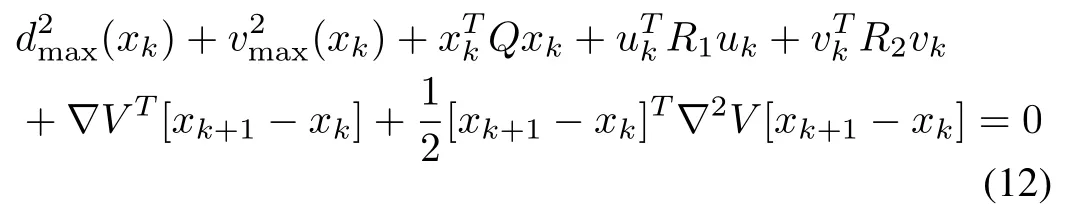
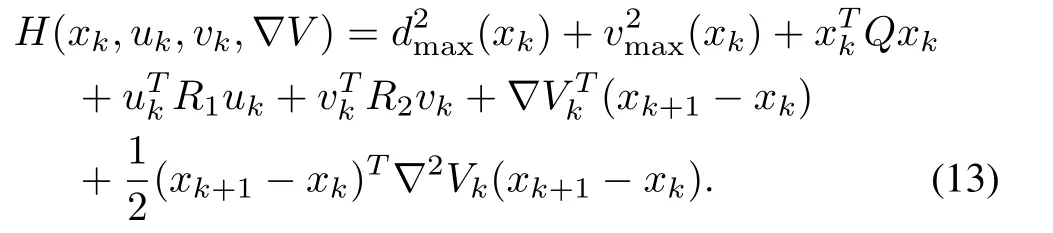
That meansandwhich correspond to

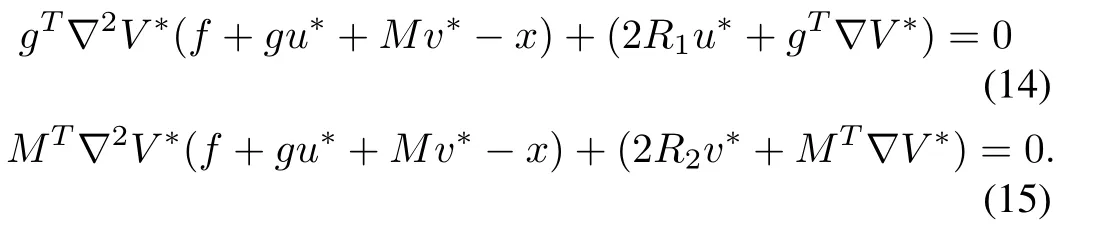
The scalarV?(xk)is the optimal value ofV(xk)and it satisfies equation(12).After further simplification,from(14)and(15),the optimal inputs are

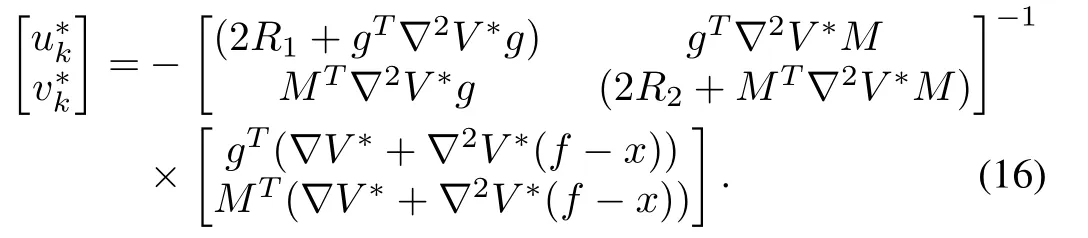
To address the stability issue of virtual nominal system(8)by applying the optimal inputs(16),following Lemma is used.

Lemma 1:Suppose there exists a Lyapunov functionV(xk)for(8)and DT-GHJB(12)is satisfied.Then the optimal inputsanddefined in(16)ensure the asymptotic convergence of virtual nominal system(8).

Proof:ConsiderV(xk)is a Lyapunov function for(8).Using(12),the ΔV(xk)=Vk+1?Vkreduces to

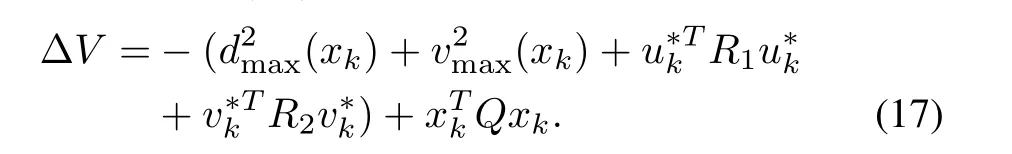
The negative-definiteness of ΔValong the solution of(8)proves the asymptotic stability of(8)through the inputs(16).

Remark 1:In DT-GHJB,the derivative of cost-functional is linearly related but it is nonlinear for DT-HJB.As a result,solving DT-GHJB corresponds to solving a linear partial difference equation.This makes the DT-GHJB computationally easier to solve than the DT-HJB.However it is still difficult to achieve a closed form solution as it is a partial difference equation.

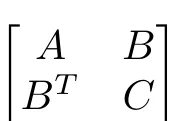
Now,the control inputs(16)can be computed if the matrix

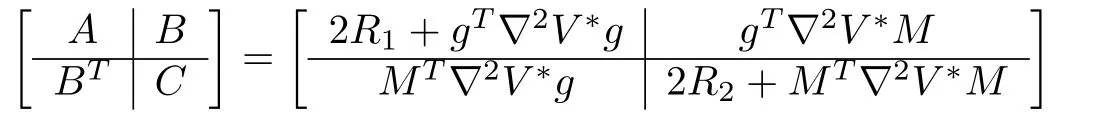
is invertible.HereR1,R2and??2Vare the positive definite matrices.So the sub-matrixis positive definite asand henceNow a suitable selection of design matricesR1andR2helps to satisfy condition 2).

The realization of optimal control inputs(16)depend on the solution of DT-GHJB(12).In the next section,a brief description of NN based approximation technique is discussed to achieve the estimated solution of(12)which helps to design the optimal inputs(16).

A.NN Based Approximation Using Least Squares Approach

Neural network(NN)has universal function approximation property.Using this approximation property,several researchers have used NN to approximate the solution of HJB orGHJB as reported in[6],[20]and[21].The key aim of this section is to approximate the optimal cost functionalV?(xk),using a NN based algorithm.Applying NN based algorithm,the cost-functionalis approximated as.The estimated cost functionalis used to compute the approximate control inputs?ukand?vk.To estimateusing NN,the basis functionand weight vectorare selected.The scalarldenotes the number of hidden layers in the NN.The selection of activation function depends on the following polynomial[17],[18]

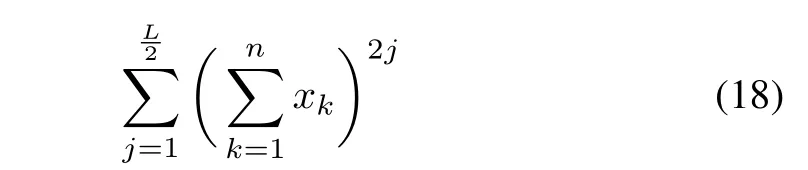
whereLandnrepresent the order of approximation and the dimension of the system respectively.The equation(19)corresponds to the activation function for a 2-dimensional system as

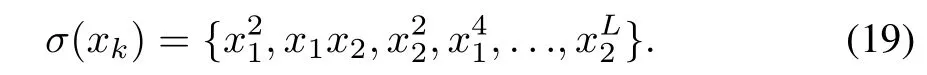
The selected basis functionσ(xk)is smooth and continuous moreover it also holds the propertyσ(0)=0,?xk=0.Applying the basis functionσ(xk)and NN weight?w,the estimated cost functional reduces to

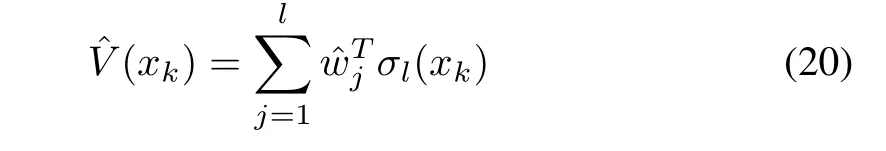
with a residual error(er)

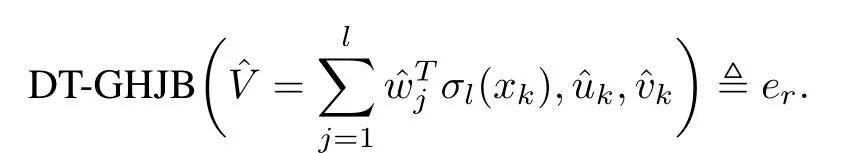
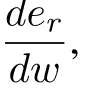
This helps to derive the weight update law with least square error minimizing rule as

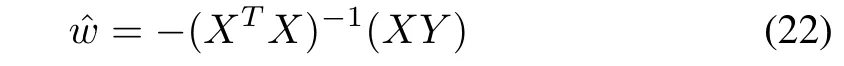
whereXandYare defined as(23)and(24),shown at the bottom of this page.

Using estimated weight(22),the cost-functional is also estimated by applying(20).The estimated cost-functional(20)is applied to derive the approximated control inputsandAn algorithmic representation of numerical steps to achieve the suboptimal inputsandis given next.

Remark 3:Given admissible control inputsu0∈?uandv0∈?v,the solutionof DT-GHJB(12)iteratively converges to its optimal solutionV?by updating the control inputs using(25).This claim can be proved analytically using the results reported in[17],[21].

B.Stability of Uncertain Systems Using Approximate Inputs

The derived approximated optimal inputs(26)for(8)ensure the asymptotic stability of uncertain system(3).This information is stated as a theorem in Algorithm 1.

Theorem 1:Suppose there exists a continuously differentiable positive function?V?(xk)which satisfies(12)with the inequality

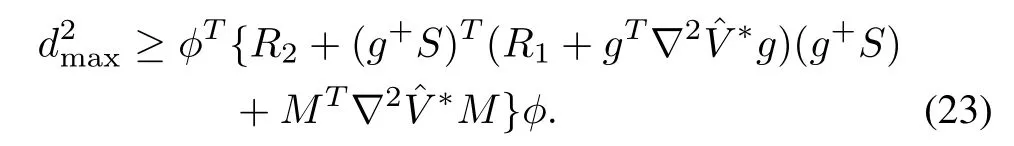
The approximated optimal control inputdefined in(26)for(8)will be the robust solution of unmatched system(3)if the following condition holds

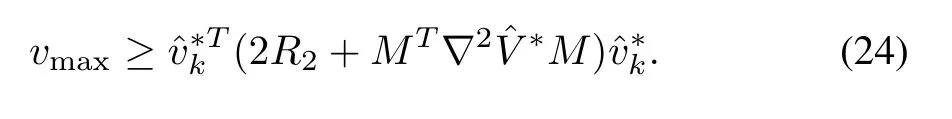
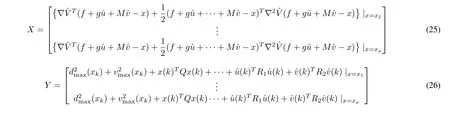
Algorithm 1 Optimal inputs using NN based approximation

Proof of Theorem 1:LetV(xk)is the solution of(12)and it is approximated asusing the estimated inputs(26).The approximated solution?V?(xk)and inputs(26)also satisfy the following equation

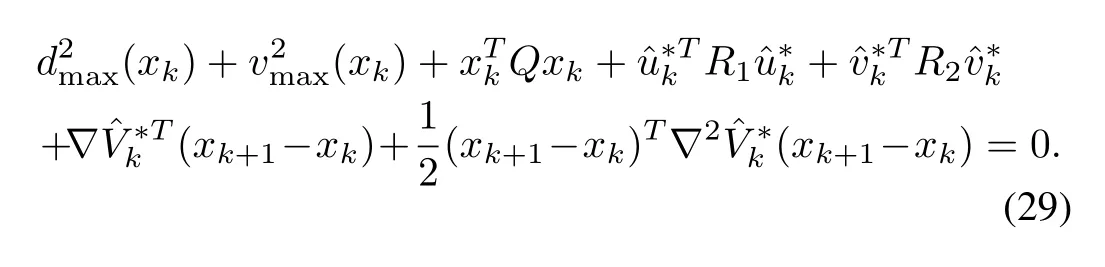
Now,with the control inputs(26),the difference ofalong the solution of(3)is

Using(7)in(30),the following is obtained

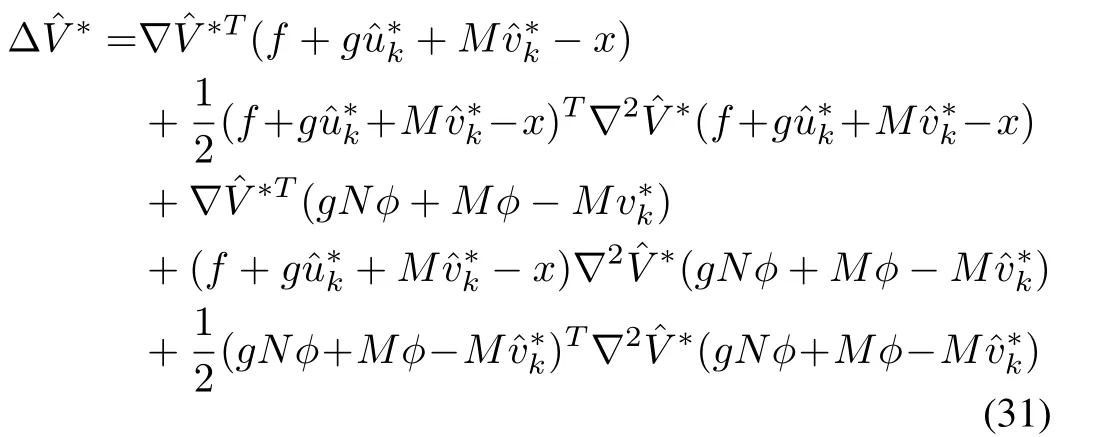
where matrixN=g+S.After further simplification,equation(26)can be rewritten as

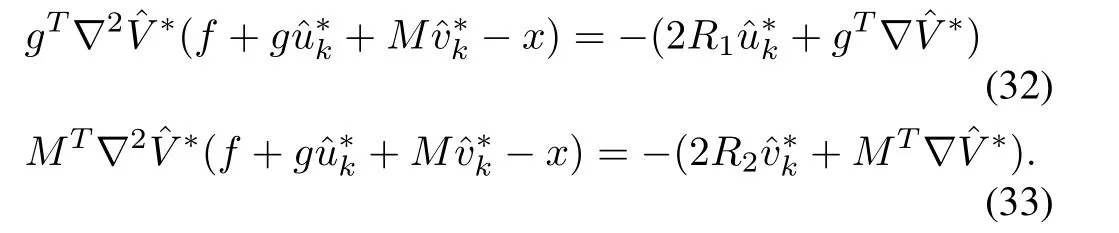
Applying(29),(32)and(33)in(31),is simplified as

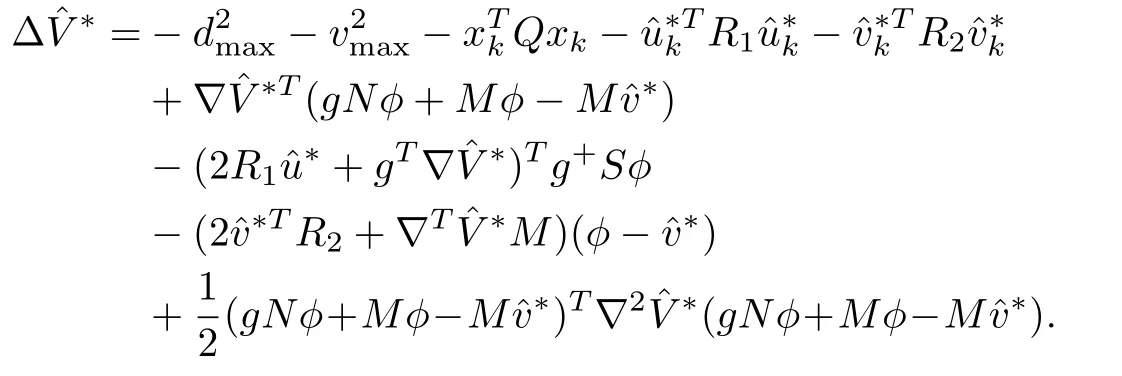
After further simplificationreduces to

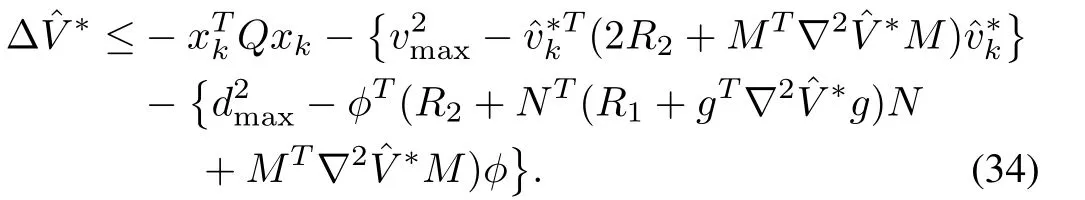
The proposed robust control framework considers the general system uncertainty,which includes both matched and mismatched component.Without mismatched part,system(3)reduces to matched system(defined in(5)),i.e.

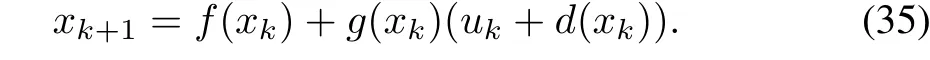
Moreover,due to the absence of mismatched part,the virtual control inputvkis not necessary in(8)and(9).Therefore the nominal system and cost-functional for(35)reduce to

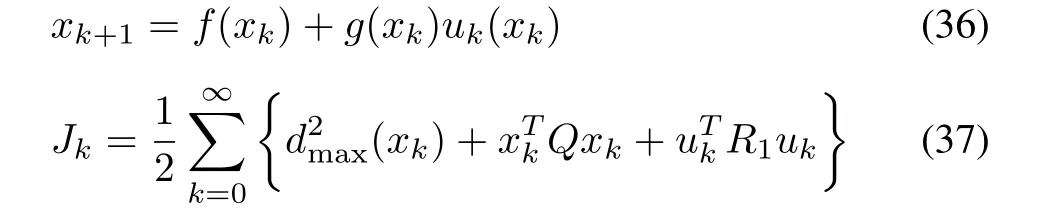
where

As a special case of Theorem 1,Corollary 1 is introduced for matched system.

Corollary 1:Suppose there exists a continuously differentiable positive functionwhich satisfies

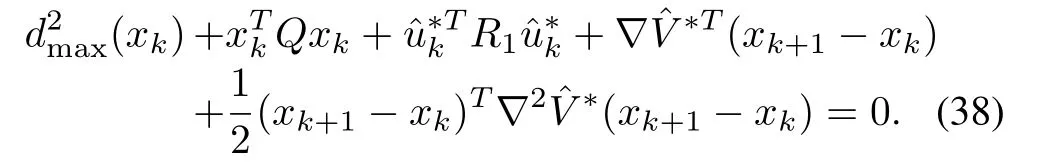
Then the designed optimal control input

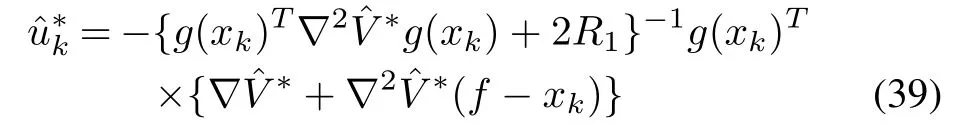
for(36)which minimizes(37)is also a robust solution of(35)if the uncertaintyd(xk)satisfies the following bound

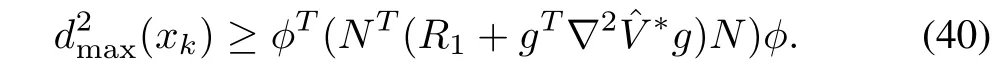
Proof:Due to space limitation,the proof of this corollary is omitted.

C.Robustness With Input Uncertainty

The proposed framework can be extended in the presence of input uncertainty.A system with mismatched input uncertainty is described as

where functiond(xk)is the bounded uncertainty affecting the input functiong(xk).To design the robust control input the virtual nominal system(8)and cost-functional(9)are considered.To tackle the mismatched uncertainty in input function,the optimal control problem is solved for(8)and(9)with the control inputs(26).The following theorem states the robust problem under presence of input uncertainty.

Theorem 2:Suppose there exists a continuously differentiable positive function?V?(xk)which satisfies(29)with the inequality

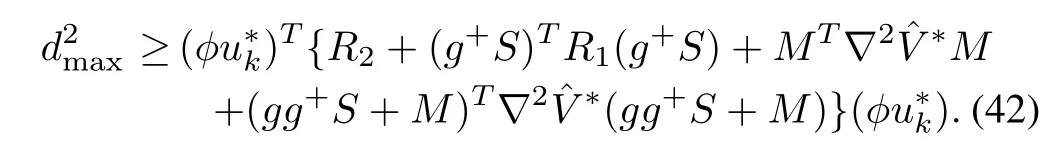
The approximate optimal control inputdefined in(26)for(8)which minimizes(9)will be the robust solution of(41)if the following condition holds

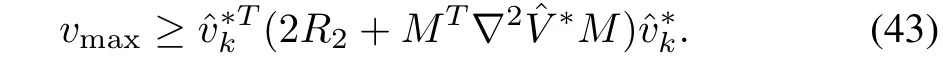
Proof:The proof of this theorem is similar to the proof of Theorem 1.

Remark 4:It is observed that the DT-HJB(10)is approximated using Taylor series expansion and it reduces to DTGHJB(12).Due to this approximation,the optimal input(11)is converted to near optimal input(16).The approximated virtual inputis not used to stabilize system(3)but it is used to design theThe inputis used to verify the condition(28).

D.Comparison With Existing Results

This subsection compares the main results of this paper with the existing work reported in[8].In 2016,D.Wanget al.have proposed an approximate optimal control based robust control technique for discrete-time nonlinear system.To realize the robust control law,they have considered that the system is affected by matched uncertainty.For the purpose of comparison with the results described in[8],the mismatched component of the uncertainty is neglected.It is observed that without mismatched component,the virtual inputvkis not necessary.Therefore without virtual inputvk,the nominal dynamics and cost-functional defined in this paper are in a form similar to that as mentioned in[8].

So the results reported in[8]can be recovered as a special case of the proposed work.To solve the nonlinear optimal control problem,a NN based approximation technique is adopted from[8],[21].But,the presence of control inputvkin nominal system(8)modifies the DT-HJB equation reported in[8],[21].To tackle the mismatched uncertainty,the cost functional(9)consists of two extra terms asandThese two extra terms directly affect the computation of matricesXandYas mentioned in(23)and(24)respectively.Moreover,the computation of approximated cost functional?V?also depends on both the control inputsandThe absence of virtual inputvkin[8],[21],makes it easy to compute?V?.

III.ADDITIONAL RESULTS

A discrete-time linear system with state uncertainty is described as

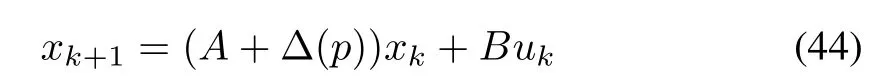
whereAandBare state and input matrices.The uncertain matrixaffects the system due to bounded variation of the uncertain parameterp.The uncertainty is bounded by a known matrixFand it is defined as

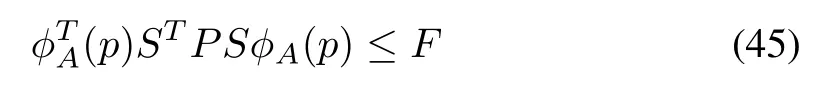
where matrixPis a positive-definite matrix.To solve the robust control problem,the virtual nominal system and cost functional are selected as

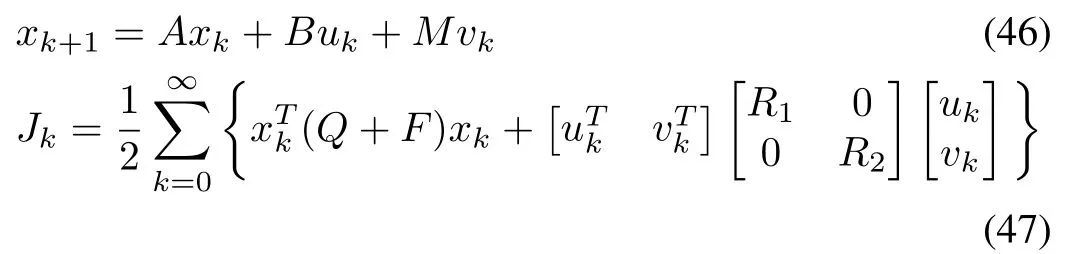
where matrixM=(I?BB+)S.With a quadratic Lyapunov functionV?(x)=xTk Pxk,the gradient vector and Hessian matrix can be expressed as?V=2Pxkand?2V=2P.For the system(46),with a cost-functional(47),the DT-GHJB is

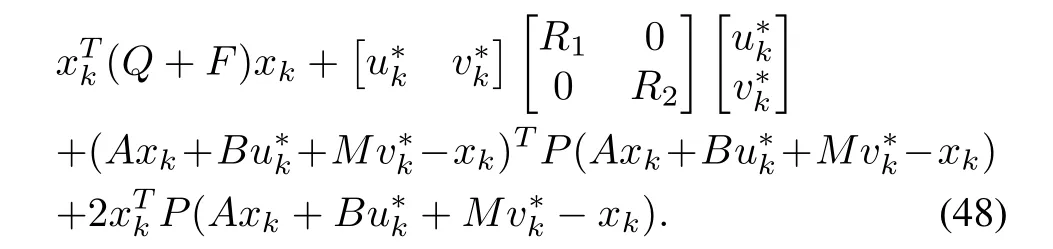
After further simplification,equation(48)reduces to

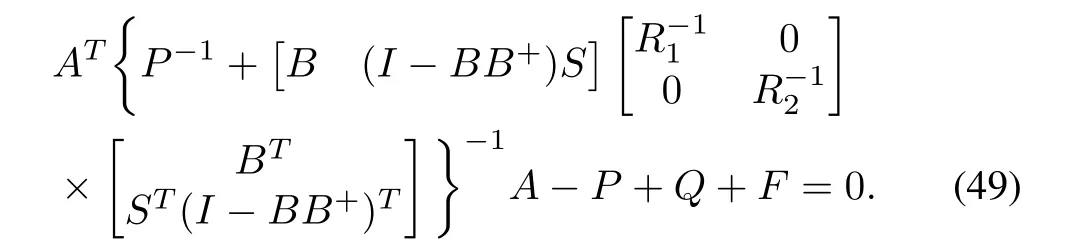
The optimal control inputsandare

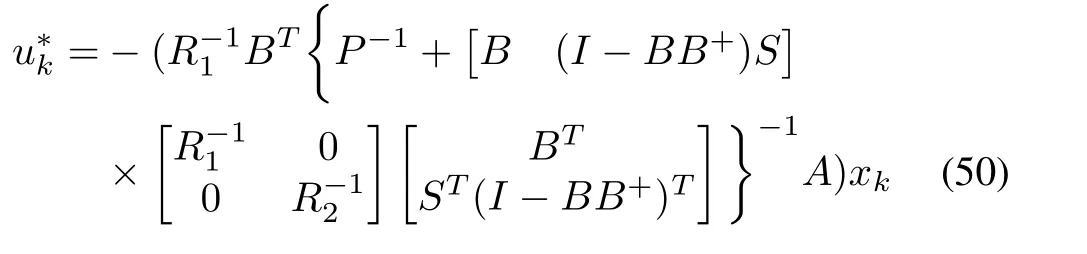
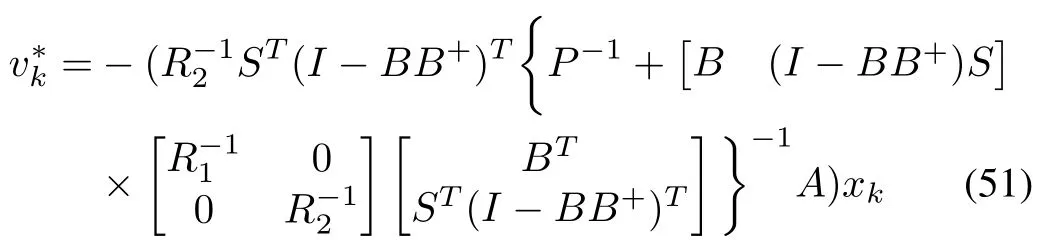
where matricesKandLare the controller gains.It is observed that the equation(49)is a discrete-time Algebraic Riccati equation(DT-ARE).Therefore the DT-ARE related with the optimal control problem for a linear system can be recovered from the proposed DT-GHJB(12).To address the robust control problem for the linear system(44),following lemma is included.

Lemma 2:Suppose their exists a positive definite solutionPof Riccati equation(49).The optimal input(50)ensures the asymptotic convergence of uncertain closed-loop system(44)for all bounded variation of uncertain parameterp,if it satisfies the inequalities(45)andwhereAc=A+BK.

Proof:Proof of this Lemma is omitted.

IV.RESULTS

The section uses a numerical example to validate the proposed control algorithm.Consider a state space form of uncertain discrete-time nonlinear system as(3)where functionsf(xk),g(xk)andφ(xk)are defined as

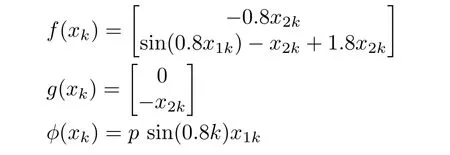
wherepis the uncertain parameter.This system has mismatched uncertainty and hence the results of[8]are not applicable.To solve the optimal control problem for virtual nominal system,the design parametersQ=I,R1=0.5IandR2=0.5Iare selected.The scaling matrixSis selected asS= ￡0.1 0.2?T.The upper bound of uncertaintyd(xk),defined in(4)is considered asdmax=‖xk‖2.The parameterpcan vary within?0.5 to 0.5.To estimate the optimal cost function through the NN realization,the NN is constructed as

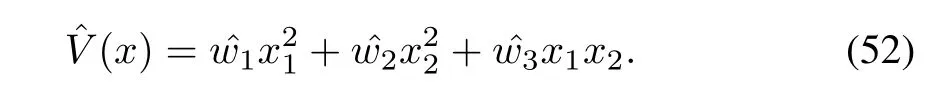
The mesh pointρ=6 and mesh size Δx=0.01 are selected.For simulation,the initial admissible control inputsu0=x1+1.5x2andv0=0.049x1are used.The simulation is carried out in MATLAB simulation platform for 10 iterations with the initial states[0.5,?0.5]T.After 5 iterations,the NN weightwconverges to

Analysis of Simulation Results:Fig.2(a)shows that the system has converged to its equilibrium point through the admissible control inputsu0.Figs.3(a)and 3(b)show the convergence of NN weight and approximated value function.In Fig.2(b),the systems state trajectories reach their equilibrium point in-spite-of uncertainty.The simulation results show that the proposed robust suboptimal control technique guarantees the closed-loop stability in presence of mismatched uncertainty.The variation of stabilizing inputand virtual inputis shown in Figs.4(a)and 4(b).

Now,for a selection of the scaling matrixS=g(xk),the same example is solved numerically.This selection converts them is matched system(3)to a matched system as defined in(35).The closed loop behavior of(35),is shown in Fig.5a and 5b which replicates the results of matched system as stated in[8].

Fig.2.Results of proposed robust control technique.(a)Convergence of state trajectory(x1,x2)with the initial admissible control inputs u0 and v0 for p=0.(b)Convergence of state trajectory(x1,x2)with the designed robust control input?u?k for p=0.5.

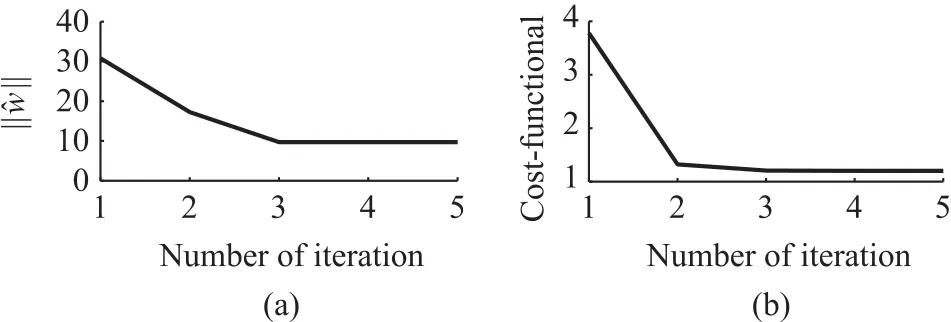
Fig.3.Results of NN based approximation.(a)Convergence of norm of weight vector(‖?w‖).(b)Convergence of approximated cost-functional.

Fig.4.Convergences of control inputs.(a)Convergence of approximated control input(b)Convergence of approximated virtual input

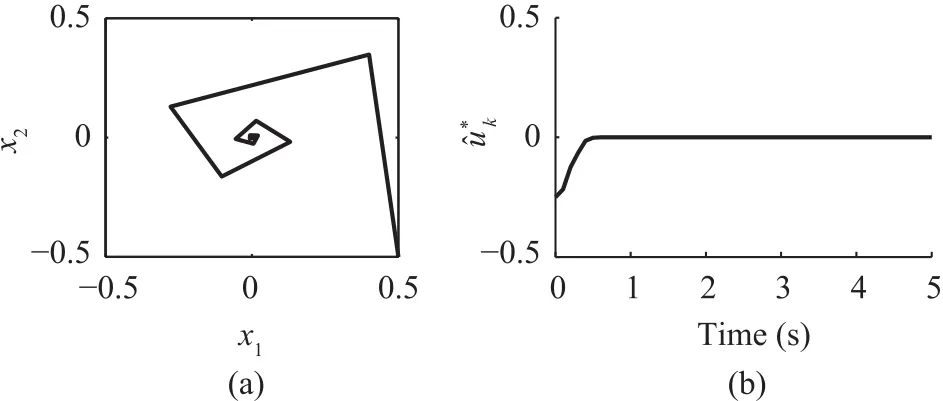
Fig.5.Results for matched uncertain system.(a)Convergence of system states with matched uncertainty for p=0.5.(b)Convergence of approximated control input for matched system.

V.CONCLUSION

A discrete-time robust control technique for an uncertain nonlinear system is proposed in this paper.It is considered that the system is primarily affected by mismatched uncertainty.The control law is designed by formulating an optimal control problem for a virtual nominal system with a modified cost functional.The virtual input is defined to design the stabilizing controller gain along with the stability condition.An analytical proof for ensuring asymptotic convergence of closed-loop uncertain system is also given.A comparative study between existing and proposed results is also reported.This paper has several promising future research directions.Few of them are discussed below.

The proposed control algorithm can be applied in several application and can also be extended to networked control system where subsystems are interconnected by a digital network[25].To address this problem,coupled DT-HJB equation can be formulated[26].The proposed control framework can also be treated as a differential game problem by considering control inputsukandvkas maximizing and minimizing inputs[27].

[1]F.Lin,“An optimal control approach to robust control design”,Int.J.Controlvol.73,no.3,pp.177?186,2000.

[2]F.Lin and R.D.Brandt,“An optimal control approach to robust control of robot manipulators”,IEEE Trans.on Robot.and Automat.,vol.14,no.1,pp.69?77,1998.

[3]F.Lin,W.Zhang and R.D.Brandt,“Robust hovering control of a PVTOL aircraft”,IEEE Trans.on Control Syst.Technol.,vol.7,no.3,pp.343?351,1999.

[4]D.Wang,D.Liu,Q.Zhang,and D.Zhao,“Data-based adaptive critic designs for nonlinear robust optimal control with uncertain dynamics”,IEEE Trans.on Syst.Man and Cybern.:Syst.,pp.1?12,2016.

[5]D.Wang,D.Liu,and H.Li,“Policy iteration algorithm for online design of robust control for a class of continuous-time nonlinear systems.”IEEE Trans.Autom.Sci.Eng.,vol.11,no.2,pp.627?632,2014.

[6]D.M.Adhyaru,I.N.Karand M.Gopal,“Fixed final time optimal control approach for bounded robust controller design using Hamilton Jacobi Bellman solution”,IET Control Theory and Appl..vol.3,no.9,pp.1183?1195,2009.

[7]D.M.Adhyaru,I.N.Kar and M.Gopal,“Bounded robust control of systems using neural network based HJB solution”,Neural Comput and Applic,vol.20,no.1,pp.91?103,2011.

[8]D.Wang,D.Liu,H.Li,B.Luo and H.Ma,“An approximate optimal control approach for robust stabilization of a class of discrete-time nonlinear systems with uncertainties”,IEEE Trans.on Syst.Man and Cybern.:Syst.,vol.46,no.5,pp.1?5,2016.

[9]IR Petersen,“Structural stabilization of uncertain systems:necessity of the matching condition”,SIAM J.Control Optim.,vol.23,no.2,pp.286?296,1985.

[10]I.N.Kar,“Quadratic stabilization of a collection of linear systems”,Int.J.Syst.Sci.,vol.33,no.2,pp.153?160,2002.

[11]Y.A.R.I.Mohamed,“Design and implementation of a robust current control scheme for a PMSM vector drive with a simple adaptive disturbance observer”,IEEE Trans.Ind.Electron.,vol.54,no.4,pp.1981?1988,2007.

[12]H.W.Lee,K.C.Kim,and J.Lee,“Review of maglev train technologies”,IEEE Trans.Magn.,vol.42,no.7,pp.1917?1925,2006.

[13]J.Yang,S.Li and X.Yu,“Sliding-mode control for systems with mismatched uncertainties via a disturbance observer”,IEEE Trans.Ind.Electron.,vol.60,no.1,pp.160?169,2013.

[14]L.Ma,Z.Wang,Y.Bo and Z.Gua,“RobustH∞sliding mode control for nonlinear stochastic systems with multiple data packet losses”,Int.J.Robust&Nonlin.Control,vol.22,no.5,pp.474?491,2012.

[15]Y.Zheng,G.M.Dimirovski,Y.jing and M.Yang,“Discrete-time sliding mode control of nonlinear systems”,American Control Conf.,New York City,USA.pp.3825?3830,2007.

[16]H.K.Khalil,Nonlinear Systems,Prentice Hall,3rd Edition,New Jersey,2002.

[17]J.Sarangapani,“Neural network control of nonlinear discrete-time systems”,CRC press,Florida,USA,2006.

[18]R.W.Beard,“Improving the closed-loop performance of nonlinear systems.”Ph.D.diss.,Rensselaer Polytechnic Institute,1995.

[19]R.A.Horn and C.R.Johnson,Matrix Analysis,Cambridge University Press,Cambridge,UK.1990.

[20]A.Al-Tamini,F.L.Lew is and M.Abu-Khalaf,“Discrete-time nonlinear HJB solution using approximate dynamic programming:Convergence Proof”,IEEE Trans.on Syst.,Man and Cybern.B:Cybern.,vol.38,no.4,pp.943?949,2008.

[21]Z.Chen and S.Jagannathan,“Generalized Hamilton-Jacobi-Bellman formulation-based neural network control of affine nonlinear discrete time systems”,IEEE Trans.on Neural Netw.,vol.19,no.1,pp.90?106.2008.

[22]D.S.Naidu,Optimal control systems,CRC press,India,2009.

[23]I.N.Imam,“The Schur complement and the inverseM-matrix problem”,Linear Algebra and its Appl.,vol.62,pp.235?240,1984.

[24]B.A.Finlayson,“The method of weighted residuals and variational principles”,Academic Press,New York,USA,1972.

[25]N.S.Tripathy,I.N.Kar,and K.Paul,“Stabilization of uncertain discrete-time linear system with limited communication”,IEEE Trans.Autom.Control,vol.62,no.9,pp.4727?4733,2017.

[26]Z.Gajic and M.T.J.Qureshi,“Lyapunov matrix equation in system stability and control”,Dover Publication,New York,USA.2008.

[27]I.R.Petersen,“Linear quadratic differential games with cheap control”,Syst.&Control Lett.,vol.8,pp.181?188,1986.