多重模糊蘊涵與生成模糊蘊涵的新方法

李 芳,裴道武

(浙江理工大學理學院,浙江杭州310018)

多重模糊蘊涵與生成模糊蘊涵的新方法

李 芳,裴道武

(浙江理工大學理學院,浙江杭州310018)

提出一種生成模糊蘊涵的新方法,即通過一個或多個選定的模糊蘊涵作多重迭代生成新的模糊蘊涵,稱為多重模糊蘊涵.從選定的模糊蘊涵出發(fā),根據(jù)不同的迭代次數(shù),分別證明迭代結(jié)果仍為模糊蘊涵.進一步,分析當選定的模糊蘊涵具有某種性質(zhì)時,所生成的多重模糊蘊涵是否仍保持這些性質(zhì).還對選定的模糊蘊涵分別為(S,N)-蘊涵和R-蘊涵這兩種重要情形,進行更深入的分析.這些結(jié)果將為模糊蘊涵在控制及決策等領(lǐng)域的應(yīng)用提供支持.

模糊邏輯;模糊蘊涵;二重蘊涵;多重蘊涵

§1 引 言

模糊蘊涵在很多領(lǐng)域都有非常重要的作用,例如模糊控制,模糊決策等.在文獻[1]中,作者主要研究模糊蘊涵在模糊控制方面的應(yīng)用,在其構(gòu)造的模糊控制系統(tǒng)中,核心組成部件是模糊規(guī)則庫,在模糊規(guī)則庫中事先給定了若干條模糊控制規(guī)則.

X和Y為論域,Ai,Bi分別為論域X和Y的模糊集(i=1,2,...,n),模糊規(guī)則庫為：

第i條規(guī)則：如果x是Ai,則y是Bi,i=1,2,...,n.

這里的第i條模糊規(guī)則為X到Y(jié)的模糊關(guān)系Ri,它由某個模糊蘊涵Ii所確定,即

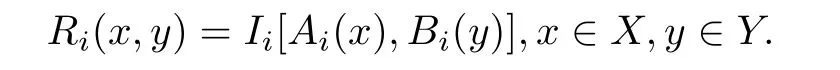
一般說來,模糊控制器的規(guī)則庫中含有足夠多的規(guī)則,這也要求有足夠多的模糊蘊涵.本文從一個或多個給定的模糊蘊涵出發(fā),通過累次迭代的方法構(gòu)造二元函數(shù),從而生成新的模糊蘊涵.還針對給定的模糊蘊涵相同與互異兩種情形,分別討論生成的模糊蘊涵及其性質(zhì).

在文獻[2]里,作者們主要研究了由兩個模糊蘊涵生成新的蘊涵,而在本文中將更一般地考慮由任意有限個蘊涵生成新的蘊涵.

§2 預(yù)備知識

本節(jié)介紹三角模,三角余模,模糊蘊涵與模糊否定的一些必要的概念與結(jié)論.

本文記U=[0,1],并且使用T,S,N和I分別記三角模,三角余模,模糊否定及模糊蘊涵.

定義2.1[3]U上的二元運算T被稱為三角模,簡稱t-模,如果T滿足交換律,結(jié)合律,單調(diào)性,并且以1為單位元.

定義2.2[3]U上的二元運算S被稱為三角余模,簡稱t-余模,如果S滿足交換律,結(jié)合律,單調(diào)性,并且以0為單位元.

定義2.3[4]U上的二元運算I被稱為模糊蘊涵,簡稱為蘊涵,如果I關(guān)于第一變元不增,關(guān)于第二變元不減,并且滿足邊界條件：I(0,0)=I(0,1)=I(1,1)=1,I(1,0)=0.

由模糊蘊涵的定義不難看出,任何模糊蘊涵必具有以下性質(zhì)：

(1)左邊界條件(LB)：I(0,y)=1,y∈U;

(2)右邊界條件(RB)：I(x,1)=1,x∈U.

定義2.4[5]U上的一元運算N被稱為模糊否定,簡稱為否定,如果N單調(diào)遞減,并且滿足邊界條件：N(0)=1,N(1)=0.

進一步,若否定N還是連續(xù)的與嚴格遞減的,則被稱為嚴格否定;若否定N還滿足對合律,即N(N(x))=x對于任何x∈U成立,則被稱為強否定.

定義2.5[6]設(shè)I為蘊涵.定義

稱NI為I的自然否定.

定義2.6[7](i)映射ρ：U→U稱為U的自同構(gòu),如果它是連續(xù)的,嚴格遞增的,且ρ(0)=0,ρ(1)=1.

(ii)設(shè)ρ是U上的自同構(gòu),F是U上的二元運算.以下定義的運算Fρ稱為F關(guān)于ρ的共軛：

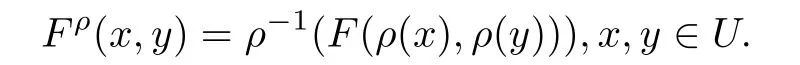
對于一些特殊類型的蘊涵,還滿足以下一些性質(zhì)[4,8,9]：

(1)左單位元性質(zhì)(NP)：I(1,y)=y,y∈U;

(2)恒等原則(IP)：I(x,x)=1,x∈U;

(3)交換原則(EP)：I(x,I(y,z))=I(y,I(x,z)),x,y,z∈U;

(4)序性質(zhì)(OP)：I(x,y)=1??x≤y,x,y∈U;

(5)強否定性(SN)：I的自然否定NI為強否定;

(6)關(guān)于否定N的逆否對稱性(CP)：I(x,y)=I(N(y),N(x)),x,y∈U.

最常見的三種模糊蘊涵的生成方式如下[6,10,11]：

(S,N)-蘊涵：由t-余模S和否定N生成,I(x,y)=S(N(x),y),x,y∈U;

R-蘊涵：為t-模T的剩余形式,即IT(x,y)=sup{z|T(x,z)≤y},x,y∈U;

QL-蘊涵：由t-模T,t-余模S,強否定N生成,I(x,y)=S(N(x),T(x,y)),x,y∈U.

§3 二重蘊涵及其性質(zhì)

首先考慮由相同的蘊涵生成新的蘊涵.

定義3.1 設(shè)I是U上的二元運算.稱以下定義的U上的二元運算FI是由I生成的二重函數(shù)：

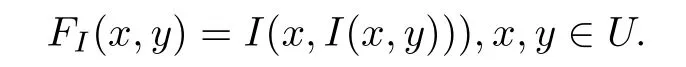
特別地,當FI為模糊蘊涵時,稱其為由I生成的二重模糊蘊涵,簡稱為二重蘊涵.

注3.1 在文獻[2]中,作者們從兩個模糊蘊涵I和J出發(fā),通過類似于定義3.1的方法,生成新的模糊蘊涵：

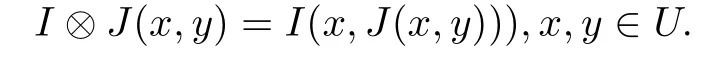
這里的模糊蘊涵的運算?被稱為?-合成.

這里只從一個二元運算I出發(fā),生成新的二元運算,與[2]是不同的.但是,當I=J為模糊蘊涵時,定義3.1可以看成[2]的特例.

例3.1 當I為Lukasiewicz蘊涵,即I(x,y)=min(1,1-x+y)時,

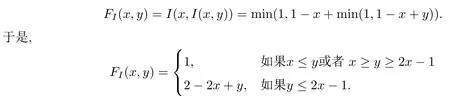
顯然,FI為模糊蘊涵.

更一般地,有以下結(jié)論：

定理3.1 當I為蘊涵時,FI也為蘊涵,即二重蘊涵.

證 作為文[2]相應(yīng)結(jié)論的特例,FI確實為蘊涵.

從例3.1可以看出,盡管蘊涵I滿足性質(zhì)(OP),但是由I生成的二重蘊涵FI卻不必滿足該性質(zhì).因此,一個自然的問題是,究竟二重蘊涵FI繼承了I的哪些性質(zhì)?

命題3.1 當蘊涵I滿足(IP)(或者(NP),(EP))時,FI也滿足(IP)(對應(yīng)地,(NP),(EP)).

證 (1)作為[2]中相應(yīng)結(jié)論的特款,當I具有性質(zhì)(IP)或(NP)時,FI也對應(yīng)地具有性質(zhì)(IP)或(NP);

(2)由I滿足(EP),對一切x,y,z∈U,I(x,I(y,z))=I(y,I(x,z)).于是,

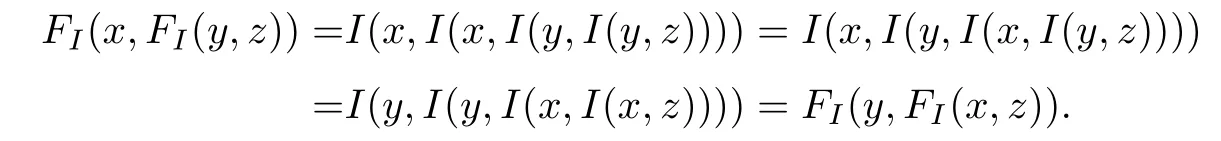
這表明,FI也滿足(EP).

注3.2 (i)文獻[2]指出,盡管兩個蘊涵I和J都滿足(EP),新的模糊蘊涵I?J也可能不滿足(EP).然而,在本文的情形,二重蘊涵FI卻保持性質(zhì)(EP).

(ii)一般說來,多重蘊涵也不保持逆否對稱性(CP).這個事實可以由以下例子得到證實.

例3.2 取I為例3.1中的Lukasiewicz蘊涵,N為標準否定,即N(x)=1-x.則由

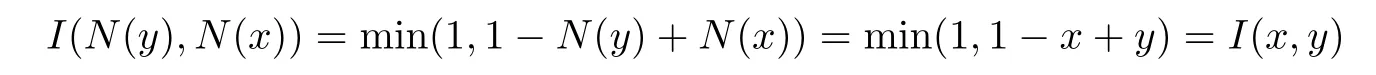
可知蘊涵I關(guān)于標準否定N滿足性質(zhì)(CP).然而

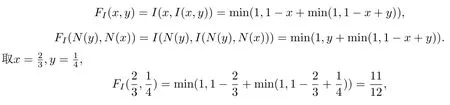
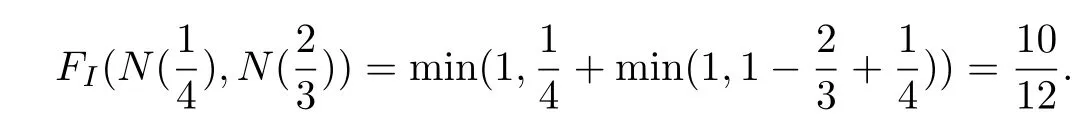
這表明FI(x,y)關(guān)于N不滿足性質(zhì)(CP).

這個例子說明二重蘊涵FI不必保持性質(zhì)(CP).

命題3.2 設(shè)I是蘊涵,ρ是U上的自同構(gòu),則二重蘊涵FI關(guān)于ρ的共軛為

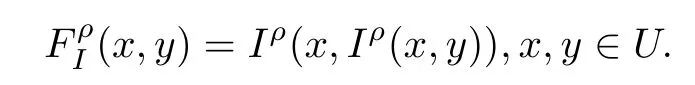
證 關(guān)于二重蘊涵F,有

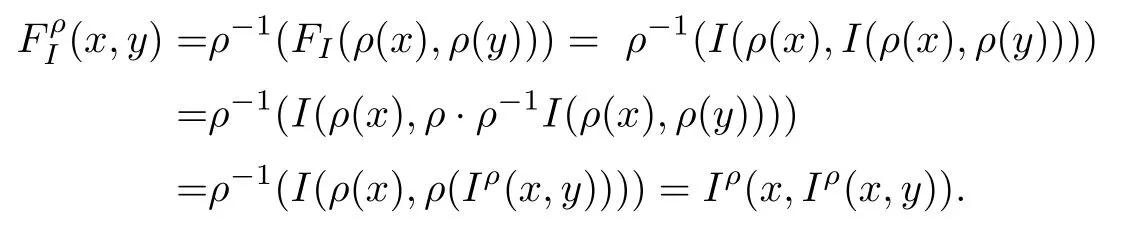
現(xiàn)在考慮由兩類特殊的模糊蘊涵生成的二重蘊涵.

命題3.3 設(shè)I為(S,N)-蘊涵,即I(x,y)=S(N(x),y),其中S,N分別為s-模與任意模糊否定,F=FI為由I生成的二重蘊涵,則

(1)F必滿足(NP);

(2)如果I滿足(IP),或者(S,N)滿足(LEM),那么F滿足(IP),其中(LEM)叫做排中律,是指S(N(x),x)=1對于任何x∈U成立;

(3)如果I滿足(SN),當S滿足(IP)時,此時S為S(x,y)=max(x,y),則F滿足(SN).

證 眾所周知,任何(S,N)-蘊涵都是蘊涵,具有性質(zhì)(NP)和(EP),而且其自然否定NI與N恰好一致[3].

(1)對一切x∈U,有F(1,x)=I(1,I(1,x))=I(1,x)=x.因此,F滿足(NP);

(2)(S,N)-蘊涵I滿足(IP)當且僅當(S,N)滿足排中律(LEM),而且此時I滿足(OP)[3].于是,對一切x∈U有

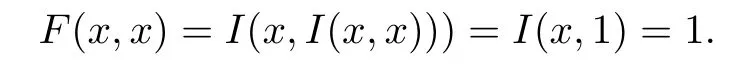
因此,F滿足(IP);

(3)由(S,N)-蘊涵I的自然否定NI與N一致,且I滿足(SN),所以對一切x∈U,有NI(NI(x))=N(N(x))=x.由S滿足(IP),得

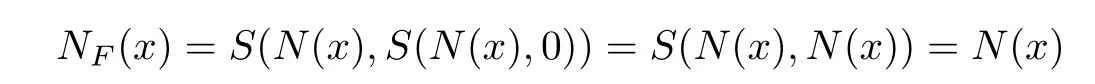
從而NF(NF(x))=N(N(x))=x,所以F滿足(SN).

對于R-蘊涵,先看下面的例子.

例3.3 取連續(xù)t-模T(x,y)=xy,則由T生成的R蘊涵為：

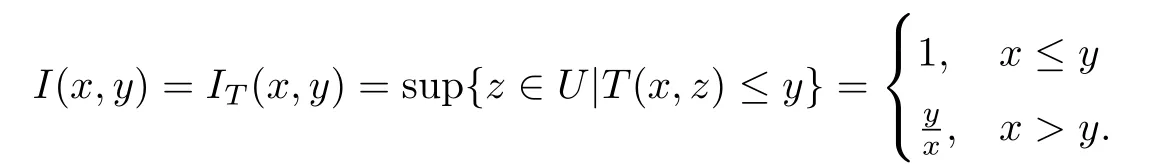
I=IT滿足交換原則(EP).取x=0.5,y=0.4,z=0.3,則

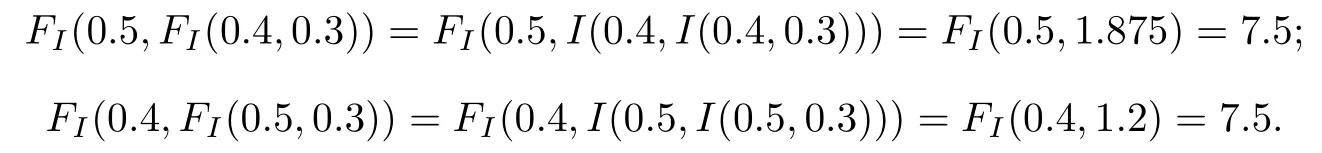
這表明,由I生成的二重蘊涵FI也滿足交換原則(EP).更一般地,有以下結(jié)論.

命題3.4 設(shè)I為由t-模T生成的R-蘊涵,而F=FI是由I生成的二重蘊涵,則

(1)F必滿足(NP);

(2)當T為左連續(xù)時,則I滿足(EP),F也滿足(EP).

證 (1)由R-蘊涵的定義容易證得;

(2)當T為左連續(xù)時,根據(jù)文獻[4]的定理2.5.7可知,I滿足(EP),再由命題3.1可知,F也滿足(EP).

§4 多重模糊蘊涵及其性質(zhì)

一般的n重模糊蘊涵是上節(jié)提出的二重模糊蘊涵的自然推廣.

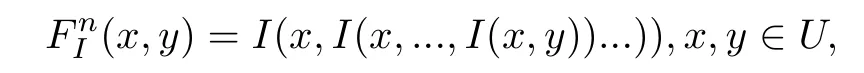
例4.1 取n=5,I為Godel蘊涵,即

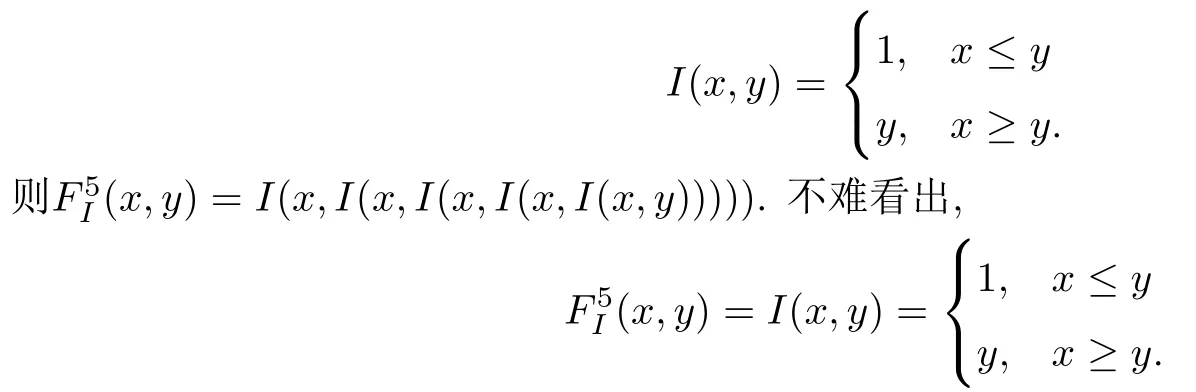
自然地,以下結(jié)論是有重要意義的.

證 只須利用定理3.1及[2]的相應(yīng)結(jié)論可得.

與n=2的情形類似,不難證明以下幾個命題成立.

命題4.1 當蘊涵I滿足(IP)(或(NP),(EP))時,也滿足(IP)(對應(yīng)地,(NP),(EP)).

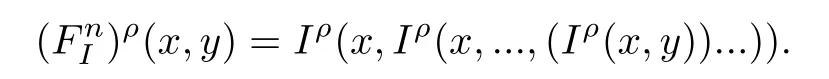
命題4.3 設(shè)I為(S,N)-蘊涵,即I(x,y)=S(N(x),y),其中S,N分別為s-模與任意模糊否定,為由I生成的n重蘊涵,則

(2)如果I滿足(IP),或者(S,N)滿足(LEM),那么滿足(IP);

注4.1 (1)由n=2的情形不難看出,當模糊蘊涵I滿足性質(zhì)(OP)(或(CP))時,不必保持這些性質(zhì);

(2)由例4.1引出一個問題,模糊蘊涵I在什么情況下,滿足=I,由其結(jié)構(gòu)形式可得,(x,y)=I(x,IN-1(x,y))=I(x,y).

情形1.I滿足(OP).則當x≤ y時,有I(x,y)=1;當x＞ y時,有I(x,y)=y.這表明I為Godel蘊涵;

情形2.I不滿足(OP).則當I(x,y)=y,且I(0,0)=1時,有

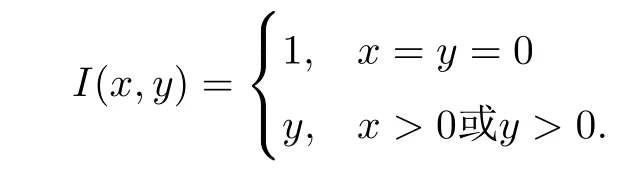
(3)與前面定義的n重蘊涵類似的函數(shù)形式有

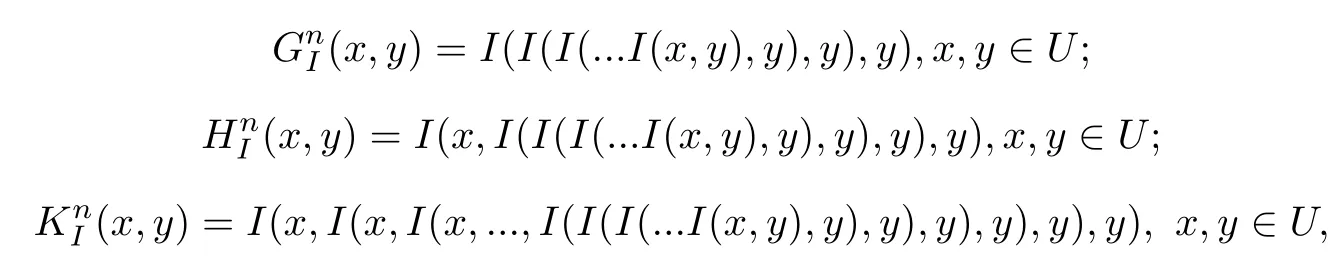
其中I為模糊蘊涵.

從而產(chǎn)生一個自然的問題,這三種迭代方式是否也可以生成模糊蘊涵?單純根據(jù)定義進行判斷,很難得出答案.而且發(fā)現(xiàn),這三種迭代方式有可能產(chǎn)生不出模糊蘊涵.這一點可從下例看出.

例4.2 對二重函數(shù)組合GI,取蘊涵I為Kleene-Dienes蘊涵,即I(x,y)=max(1-x,y),x,y∈U.則對于任何x,y∈U,有

GI(x,y)=I(max(1-x,y),y)=max(1-max(1-x,y),y)=max(min(x,1-y),y).

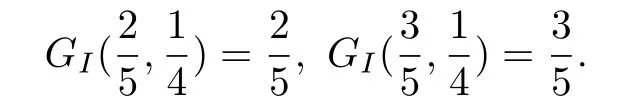
這里x1＜x2,但是,卻有GI(x1,y)＜GI(x2,y).這表明GI不是蘊涵.

至于需要對給定的蘊涵I增加哪些條件限制,才能分別保證以上迭代方式生成模糊蘊涵,仍然是一個未解決的問題.

§5 由不同的蘊涵生成的多重蘊涵及其性質(zhì)

設(shè){I1,I2,...,In}為區(qū)間U上n個模糊蘊涵構(gòu)成的集合,類似于從同一個給定的蘊涵生成n重蘊涵的形式,可以定義下面具有更廣意義的n重函數(shù)與n重蘊涵.

定義5.1 設(shè)I1,I2,...,In為n個蘊涵.U上的二元運算JI1,I2,...,In稱為由(I1,I2,...,In)生成的n重函數(shù),

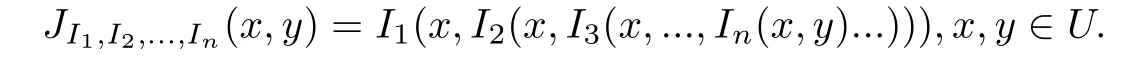
特別地,當JI1,I2,...,In為模糊蘊涵時,稱其為由(I1,I2,...,In)生成的n重模糊蘊涵,仍簡稱為n重蘊涵.

不難看出,定義5.1是定義3.1,定義4.1以及[2]中相應(yīng)概念的推廣.

例5.1 取n=3,I1為例4.1所給出的Godel蘊涵,I2為例3.1所給出的Lukasiewicz蘊涵,I3為Reichenbach蘊涵,即I3(x,y)=1-x+xy.那么

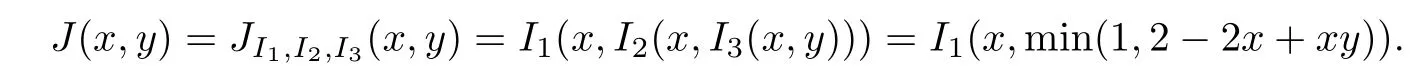
計算得到

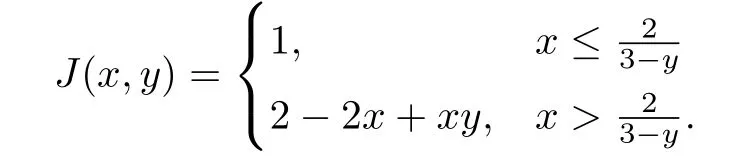
由下述命題可知,J為模糊蘊涵.

命題5.1 當I1,I2,...,In都是蘊涵時,J=JI1,I2,...,In也為蘊涵,即n重蘊涵.

證 對上述n重函數(shù)J,取x1,x2,y∈U,且x1≤x2,由I1,I2,...,In都為蘊涵,有

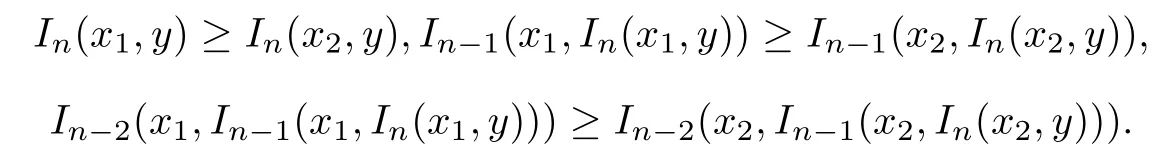
以此類推得J(x1,y)≥J(x2,y).所以,J(x,y)關(guān)于第一個變量遞減.

取y1,y2,x∈U,滿足y1≤y2.由I1,I2,...,In為模糊蘊涵,得到

以此類推得J(x,y1)≤J(x,y2).所以,J(x,y)關(guān)于第二個變量遞增.

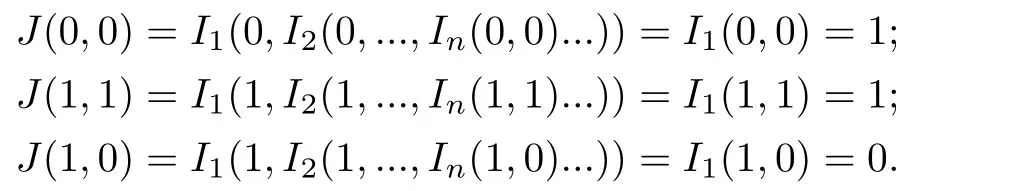
由模糊蘊涵定義可知,當I1,I2,...,In都為蘊涵時,J也為蘊涵.

命題5.2 當蘊涵I1,I2,...,In都具有性質(zhì)(NP)或(IP)時,J=JI1,I2,...,In也對應(yīng)地具有性質(zhì)(NP)或(IP).

證 (1)當I1,I2,...,In都滿足(NP)時,

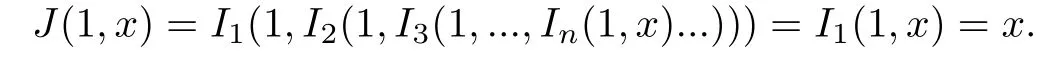
所以J也滿足(NP);

(2)當I1,I2,...,In都滿足(IP)時,

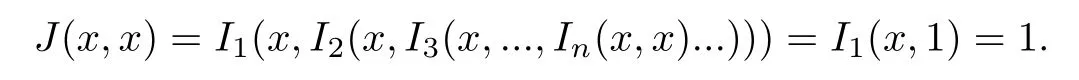
所以J也滿足(IP).

注5.1 (1)當I1,I2,...,In具有性質(zhì)(OP)或(CP)時,JI1,...,In未必對應(yīng)地具有性質(zhì)(OP)或(CP),這可以從上節(jié)看出;

(2)當I1,...,In都具有性質(zhì)(EP)時,JI1,...,In未必具有性質(zhì)(EP).這個事實可從下例看出.

例5.2 在例5.1中,蘊涵I1,I2,I3均具有性質(zhì)(EP),而且

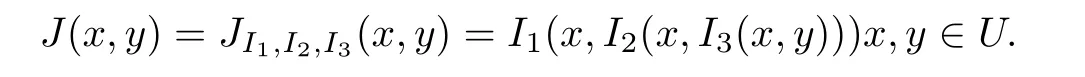
取x=0.92,y=0.85,z=0.6.則

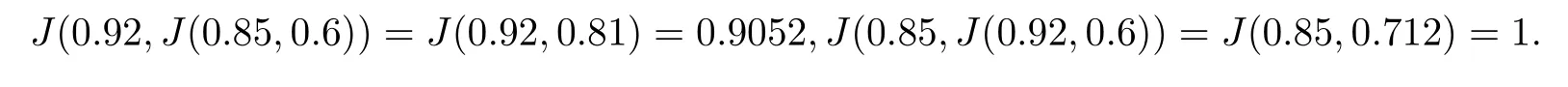
這表明J不具有性質(zhì)(EP).

命題5.3 當蘊涵I1,I2,...,In都具有性質(zhì)(ME)時,J=JI1,I2,...,In也對應(yīng)地具有性質(zhì)(EP).

證 由文獻[2]可知,取n=2,當I1,I2滿足(ME)時,JI1,I2(x,y)滿足(EP);

取n=3,當I1,I2,I3滿足(ME)時,

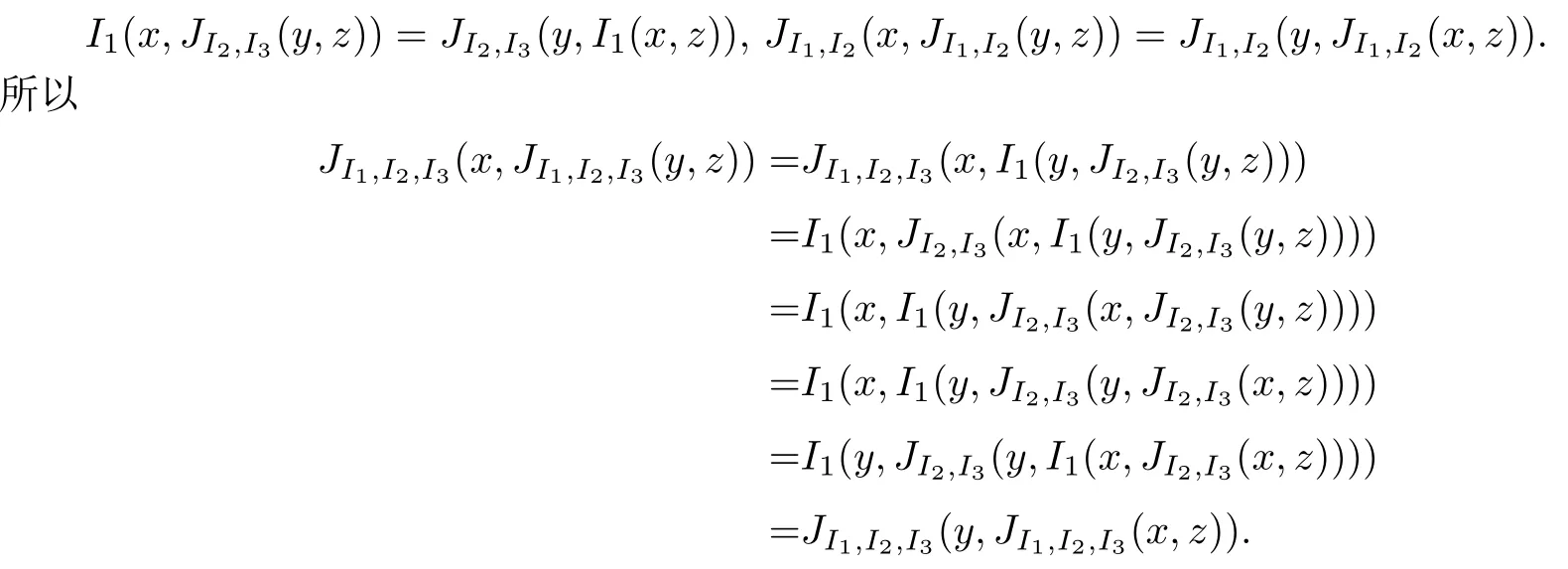
由數(shù)學歸納法得,當n為一般正整數(shù)時,JI1,I2,...,In(x,y)也滿足(EP).

§6 結(jié)論

當應(yīng)用領(lǐng)域出現(xiàn)多個模糊蘊涵時,可以通過函數(shù)組合的形式把這些模糊蘊涵組合在一起,以生成新的模糊蘊涵.本文提出一種新的模糊蘊涵生成方法,即從一個模糊蘊涵或多個模糊蘊涵,通過迭代的方法得到新的模糊蘊涵,并研究這種模糊蘊涵的性質(zhì),得到一些有趣的結(jié)論.這里的生成模糊蘊涵的方法與相應(yīng)結(jié)論推廣了文獻中已有的成果.

在以后的工作中,將考慮由這種方法生成的多重蘊涵的其他性質(zhì),如逆否對稱性(CP)等.盡管在例3.2中已經(jīng)看到,一般說來,多重蘊涵不保持(CP),但是,可以進一步討論在初始蘊涵滿足什么條件下,多重蘊涵才保持(CP).另一個需要研究的課題是,隨著重數(shù)的增加,多重蘊涵的性質(zhì)將會發(fā)生怎樣的變化.自然地,將這種方法生成的多重蘊涵應(yīng)用于實際的模糊推理問題[12,13],也是具有重要意義的.另外,還可以模糊蘊涵與模糊蘊涵代數(shù)的關(guān)系[14],考慮由聚合算子生成模糊蘊涵[15],以及模糊蘊涵的其它組合形式,例如,凸組合形式[16]等,為模糊蘊涵的實際應(yīng)用提供更多的選擇.

致謝 對審稿人提出的寶貴意見和建議表示衷心的感謝!

[1] 李洪興.Fuzzy系統(tǒng)的概率表示[J].中國科學(E),2006,36(4)：373-397.

[2] Vemuri N R,Jayaram B.The?-composition of fuzzy implications：Closures with respect to properties,powers and families[J].Fuzzy Sets Syst,2015,275：58-87.

[3] Klement E P,Mesiar R,Pap E.Triangular norms[M].Dordrecht：Kluwer,2000.

[4] Baczynski M,Jayaram B.Fuzzy implications[M].Heidelberg：Springer,2008.

[5] Benjamin C B.On interval fuzzy negations[J].Fuzzy Sets Syst,2010,161：2290-2313.

[6] Baczynski M,Jayaram B.On the characterizations of(S,N)-implications[J].Fuzzy Sets Syst,2007,158：1713-1727.

[7] Bustince H,Burillo P,Soria F.Automorphisms,negations and implication operations[J].Fuzzy Sets Syst,2003,134：209-229.

[8] Gottwald S.A Treatise on Many-Valued Logic[M].Baldock：Resarch Studies Press,2001.

[9] Smets P,Magrez P.Implication in fuzzy logic[J].Int.J Approx Reason,1987,1：327-347.

[10]Baczynski M.Residual implications revisited.Notes on the Smets-Magrez Theorem[J].Fuzzy Sets Syst,2004,145：267-277.

[11]Shi Yun,Ruan D,Kerre E.E.On the characterizations of fuzzy implications satisfying I(x,y)=I(x,I(x,y))[J].Inform Sci,2007,177：2954-2970.

[12] 裴道武.模糊推理的基本理論[J].高校應(yīng)用數(shù)學學報,2012,27(3)：340-350.

[13]裴道武.基于三角模的模糊邏輯理論及其應(yīng)用[M].北京：科學出版社,2013.

[14] 裴道武,王三民,楊瑞.模糊蘊涵格理論[J].高校應(yīng)用數(shù)學學報,2011,26(3)：343-354.

[15]Yao Ouyang.On fuzzy implications determined by aggregation operators[J].Inform Sci,2012,193：153-162.

[16]Mirko N.Convex combinations of fuzzy logical operations[J].Fuzzy Implications.Fuzzy Sets Syst 2015,264：51-63.

Multiple fuzzy implications and novel methods to generate fuzzy implications

LI Fang,PEI Dao-wu
(School of Sciences,Zhejiang Sci-Tech University,Hangzhou 310018,China)

This paper proposes some new methods for generating fuzzy implications.Some new fuzzy operations can be generated by using some selected fuzzy implications through multiple iterations.According to di ff erent iterative methods,all of the new fuzzy operations have been proved to be fuzzy implications.Furthermore,when the selected fuzzy implications satis fi ed some important properties,whether multiple fuzzy implications still keep these properties or not is also discussed.Two important cases have been investigated：the selected implications are(S,N)-implications or R-implications.This work provides some new possible selections of fuzzy implications for some applied fi elds such as fuzzy control and fuzzy decision making.

fuzzy logic;fuzzy implication;double implication;multiple implication

03B50;03B52

O141.1

A

：1000-4424(2016)04-0467-09

2016-02-25

2016-10-20

國家自然科學基金(11171308;61379018;61472471;51305400)