5元素集合上T0拓?fù)淇倲?shù)的計算

榮宇音,徐羅山

(揚州大學(xué)數(shù)學(xué)科學(xué)學(xué)院,江蘇揚州225002)

5元素集合上T0拓?fù)淇倲?shù)的計算

榮宇音,徐羅山

(揚州大學(xué)數(shù)學(xué)科學(xué)學(xué)院,江蘇揚州225002)

利用有限偏序集上的幾個重要結(jié)果并借助于拓?fù)淇臻g對應(yīng)的特殊化序與拓?fù)渲g的關(guān)系計算得出5元素集合上T0拓?fù)淇倲?shù)為4231,拓?fù)淇倲?shù)為6942.

有限偏序集;拓?fù)?極小元;T0拓?fù)淇倲?shù)

§1 引 言

拓?fù)鋵W(xué)[1]中有一個艱難的問題是給出n元素集合上拓?fù)淇倲?shù)的計算.為了計算n元集合上的拓?fù)淇倲?shù),對于較小的n可以通過手工驗證進(jìn)行計算;對于稍大一點的n則可以通過計算機(jī)編程進(jìn)行窮舉計算,但這很難體現(xiàn)數(shù)學(xué)方法和思維.當(dāng)然如果不借助于計算機(jī)編程,要算出n元素集合上的拓?fù)淇倲?shù),則可先考慮計算T0拓?fù)淇倲?shù)和非T0拓?fù)淇倲?shù),其中T0拓?fù)淇倲?shù)的計算更具方法性和技巧性,而非T0拓?fù)淇倲?shù)可以通過較小n情形的T0拓?fù)淇倲?shù)經(jīng)遞推計算得到.于是要計算n元素集合上拓?fù)淇倲?shù)關(guān)鍵是要計算n元素集合上T0拓?fù)淇倲?shù).從Domain理論與拓?fù)涞慕徊鎽?yīng)用[2-6]入手,文[7]已經(jīng)算出了對于n=1,2,3和4的T0拓?fù)淇倲?shù)分別是1,3,19和219,相應(yīng)的拓?fù)淇倲?shù)分別是1,4,29和355.隨著n的增大,計算這些總數(shù)難度會越來越大.本文從序與拓?fù)涞慕徊娉霭l(fā),在文[7]的基礎(chǔ)上并利用文[7]的理論和方法,結(jié)合Hasse圖[8],進(jìn)一步給出了5元素集合上T0拓?fù)淇倲?shù)和非T0拓?fù)淇倲?shù)的計算,它們分別是4231和2711,從而得到5元素集合上拓?fù)淇倲?shù)是4231+2711=6942.本文所用的方法還可望向n的更大情形推廣.

§2 若干相關(guān)概念和引理

先給出幾個相關(guān)概念,它們大都采自文獻(xiàn)[2]和[8].

設(shè)X為集合,則X上的自反且傳遞的二元關(guān)系均稱為X上的預(yù)序,記為≤.X上的一個預(yù)序,如果還是反對稱的,即由x≤y≤x可得x=y,則稱這樣的預(yù)序為偏序.設(shè)≤為X上一個預(yù)序(或偏序),則稱(X,≤)為一個預(yù)序集(或偏序集).此時也稱X為一個預(yù)序集(或偏序集).

設(shè)(X,≤)為偏序集.對x,y∈X,用x＜y表示x≤y且x 6=y.若x＜y不成立,則記為x≮y.

設(shè)X為預(yù)序集,m∈X稱為一個極小元,如果X中任一元x,當(dāng)x≤m時,有m≤x成立.X的非空子集D稱為X的定向集,若對任意a,b∈D,存在c∈D使a≤c,b≤c.

設(shè)A ? X,記↑A={y∈X ：?x∈A,x≤ y}及↓A={y∈X ：?x∈A,y≤ x}.簡記↑{y}為↑y及↓{y}為↓y.

定義2.1[2,6]設(shè)X為預(yù)序集,A?X.A稱為X的Scott-閉集,如果滿足：(1)A=↓A;(2)對任意定向集D?A,若上確界supD存在,則有supD∈A.X上的全體Scott-閉集記為σ?(X).X上Scott-閉集的補(bǔ)集全體形成X上的拓?fù)浞Q為Scott拓?fù)?記作σ(X).

易知偏序集上的Scott拓?fù)渚鶠門0拓?fù)?又如X是有限預(yù)序集,則σ(X)={↑A|A?X}為X的全體上集.

定義2.2[2,6]設(shè)X為拓?fù)淇臻g.X上的特殊化序≤定義為x≤y當(dāng)且僅當(dāng)x∈{y}-,其中{y}-為獨點集{y}的閉包.

下列命題和引理的是本文的理論基礎(chǔ),證明詳見文獻(xiàn)[7]中相應(yīng)結(jié)論的證明,這里從略.

命題2.1 預(yù)序集X的序和其上Scott拓?fù)涞奶厥饣蚴且恢碌?又若X為T0拓?fù)淇臻g,則X上特殊化序為偏序.若X為非T0拓?fù)淇臻g,則X上特殊化序為預(yù)序而非偏序(這樣的預(yù)序稱為真預(yù)序).

引理2.1 設(shè)X為有限集,τ和η為X上兩個拓?fù)?則τ=η當(dāng)且僅當(dāng)它們誘導(dǎo)的特殊化序相同.又設(shè)≤1和≤2為X上兩個預(yù)序,該兩預(yù)序相同當(dāng)且僅當(dāng)它們誘導(dǎo)的Scott拓?fù)湎嗤?

注2.1 (1)對于無限集,其上兩個不同的拓?fù)淇烧T導(dǎo)相同的特殊化序,例如有限補(bǔ)拓?fù)浜碗x散拓?fù)湔T導(dǎo)的特殊化序均為離散偏序.

(2)上一引理是說,有限集上的拓?fù)渑c其上的預(yù)序形成一一對應(yīng)且T0拓?fù)鋵?yīng)于偏序,而非T0拓?fù)鋵?yīng)于真預(yù)序.

引理2.2 (Zorn引理)在任何一個非空的偏序集中,如果任何一個全序子集都有上界,那么這個偏序集必然存在極大元.對偶地,在任何一個非空的偏序集中,如果任何一個全序子集都有下界,那么這個偏序集必然存在極小元.

引理2.3 設(shè)X為偏序集,min(X)為X的極小元之集.則當(dāng)x∈Xmin(X)時,斷言存在y0∈X使y0＜x.

引理2.4 設(shè)X為有限偏序集,min(X)為X的極小元之集.則?y∈X有↓y∩min(X)6=?.

定理2.5 設(shè)X為有限偏序集,min(X)為X的極小元之集,則當(dāng)x∈Xmin(X)時,存在m0∈min(X)使m0＜ x.

§3 5元素集合上非T0拓?fù)鋽?shù)計算

由引理2.1知,n元素集合上非T0拓?fù)鋽?shù)對應(yīng)的是n元素集合上真預(yù)序數(shù).對于真預(yù)序集,滿足條件x≤y≤x的元x和y稱為等價元.當(dāng)然,一個真預(yù)序集至少有兩個元等價.用Yi和Pi分別表示i個元素集合上真預(yù)序數(shù)和偏序數(shù).由文[7]知,Y1=0,P1=1,Y2=1,P2=3,Y3=10,P3=19,Y4=136,P4=219.

下面計算Y5而得到5元素集合上非T0拓?fù)鋽?shù).我們將按等價元的個數(shù)進(jìn)行分類計算.

情形1：含5個等價元,即5個元均等價,共有一種真預(yù)序.

情形2：含4個等價元,此時有4個元相互等價,該4元可看成一個整體,與剩下的一個元形成二元偏序,這種情形共有×P2=×3=15個真預(yù)序.

情形3：含3個等價元,這時又有兩種情況.一是除3等價元外,剩下的兩元不等價,這時將3等價元看成整體與剩下兩元形成3元偏序,這種情況共有

個真預(yù)序;二是除3等價元外,剩下的兩元也等價,這時將兩組等價元看成兩個整體形成二元偏序,這種情況共有

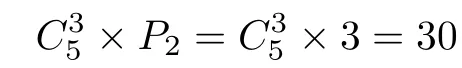
個真預(yù)序.故情形3共有190+30=220個真預(yù)序.

情形4：含兩個等價元,這時又有兩種情況.一是除兩等價元外,剩下的3元不等價,這時將兩等價元看成整體與剩下3元形成4元偏序,這種情況共有

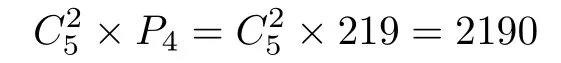
個真預(yù)序;二是除兩等價元外,剩下的3元中有兩元也等價,這時將兩組等價元看成兩個整體與剩下一元形成3元偏序,注意到對稱性,這種情況共有

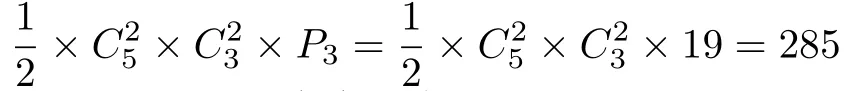
個真預(yù)序.故情形4共有2190+285=2475個真預(yù)序.

四種情形合計共有真預(yù)序數(shù)為1+15+220+2475=2711.

綜之,5元素集合上共有2711個真預(yù)序,即Y5=2711,從而其上共有2711個非T0拓?fù)?

§4 5元素集合上T0拓?fù)鋽?shù)計算

由引理2.1,為計算5元素集合上T0拓?fù)鋽?shù),只需計算5元素集合上偏序數(shù)P5.下面依極小元個數(shù)進(jìn)行分類計算.

情形1：含5個極小元,這時是離散偏序,僅有1個偏序.

情形2：含4個極小元(見圖1).這時4個極小元相互不可比較,又由定理2.5,剩下的一個元至

圖1 含4個極小元

少大于一個極小元,也可能大于兩個或3個或4個極小元,這種情形共有偏序數(shù)為

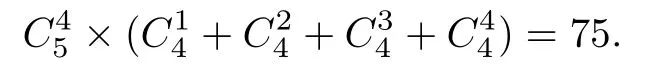
情形3：含3個極小元,此時分兩種情況.

(1)剩下兩元不可比較(見圖2).則每元與3極小元形成偏序數(shù)分別為++=7,這

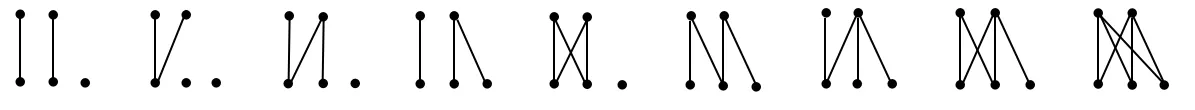
圖2 含3個極小元(1)

種情況共有偏序數(shù)為

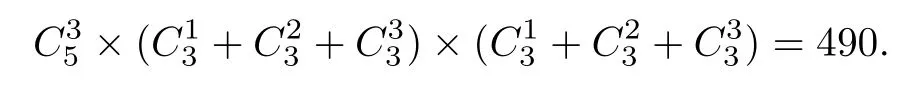
(2)剩下的兩元可比較(見圖3).由定理2.5,該兩元中的較小元至少比一個極小元大,當(dāng)較小

圖3 含3個極小元(2)

元比3極小元中的1個大時,較大的元可比另外二個極小元中0個或1個或2個大,共有×(++)=12種選擇;若較小的元比其中兩個極小元都大時,這時較大的元可比另外一個極小元中0個或1個大,共有×(+)=6種選擇;若較小的元比3個極小元都大時,這時有=1種選擇,從而這種情況共有偏序數(shù)為

故情形3兩種情況合計共有490+380=870種偏序.

情形4：含2個極小元,此時分三種情況.

(1)剩下3元不可比較(見圖4).則每元與兩極小元形成偏序數(shù)分別為+=3,這種情況

圖4 含2個極小元(1)

共有偏序數(shù)為

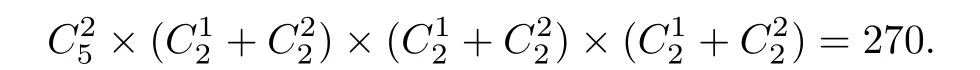
(2)剩下的3元中至少有兩元可比較,此時這3元按極大元的情況可以分成兩類.

(I)極大元有兩個(見圖5).此時若(A)兩極大元都比剩下的第三元大時有=3種,由定

圖5 含2個極小元(2)-(I)

理2.5,該第三元至少比一個極小元大,當(dāng)該第三元比兩極小元中的1個大時,兩極大元都可比另外一個極小元中0個或1個大,共有×(+×(+)=8種選擇;若該第三元比兩個極小元都大時有=1種選擇.于是,情形4(2)(I)(A)共有偏序數(shù)為

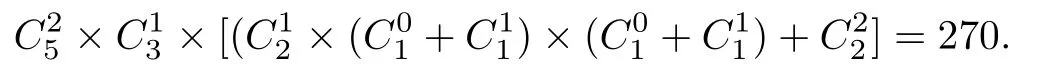
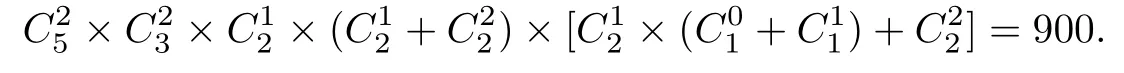
故情形4(2)(I)共有偏序數(shù)為270+900=1170.

(II)極大元有一個(見圖6).此時剩余兩較小元,每個較小元至少比一個極小元大,每個較小

圖6 含2個極小元(2)-(II)

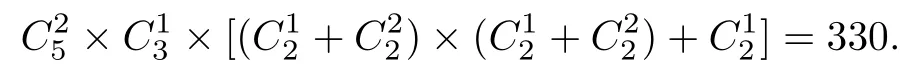
綜之,情形4(2)共有偏序數(shù)為1170+330=1500.

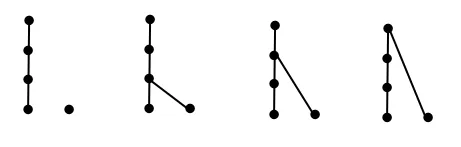
圖7 含2個極小元(3)

故情形4(3)共有偏序數(shù)為

綜之,情形4的三種情況合計有270+1500+420=2190個偏序.

情形5：含1個極小元(見圖8).這時由定理2.5,該極小元也是最小元,從而剩下的4個元形成4元偏序,這種情形共有偏序數(shù)為

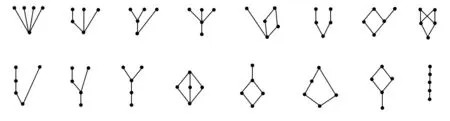
圖8 含1個極小元

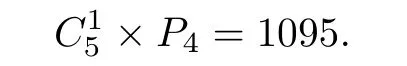
于是,5元素集合上偏序數(shù)P5=1+75+870+2190+1095=4231.從而5元素集合上T0拓?fù)鋫€數(shù)為4231.

綜之,5元素集合上非T0拓?fù)鋽?shù)為2711,T0拓?fù)鋽?shù)為4231,而不同拓?fù)淇倲?shù)為6942.

§5 結(jié)論

本文利用偏序與拓?fù)渲g的關(guān)系以及有限預(yù)(偏)序集的性質(zhì)給出了5元素集合上非T0拓?fù)淇倲?shù)和T0拓?fù)淇倲?shù)的計算.結(jié)果是：5元素集合上非T0拓?fù)鋽?shù)為2711,T0拓?fù)鋽?shù)為4231,而不同拓?fù)淇倲?shù)為6942.

這種計算方法易于被人們理解,并可望向n=6,7甚至更大的n情形推廣.

致謝 揚州大學(xué)數(shù)科院研究生陳振超利用計算機(jī)編程驗證了本文的上述結(jié)果,特此致謝.

[1] Engelking R.General topology[M].Warszawa：Polish Scienti fi c Publishers,1977.

[2] Gierz G,Hofmann,K H,Keimel K,et.al.Continuous Lattices and Domains[M].Cambridge：Cambridge University Press,2003,1-263.

[3] Lawson J D.The duality of continuous posets[J].Houston Journal of Mathematics,1979,5：357-394.

[4] Scott D.Continuous lattices[J].Toposes,algebraic geometry and logic,Lecture Notes in Mathematics,Berlin：Springer,1972,274：97-136.

[5] Xu Luoshan.Continuity of Posets via Scott Topology and Sobri fi cation[J].Topology and Its Applications,2006,153：1886-1894.

[6] 何青玉,徐羅山.Scott閉集格的C-代數(shù)性及其應(yīng)用[J].高校應(yīng)用數(shù)學(xué)學(xué)報,2014,29(3)：369-374.

[7] 榮宇音,徐羅山,謝麗娜.有限偏序集與4元素集合上T0拓?fù)淇倲?shù)的計算[J].高校應(yīng)用數(shù)學(xué)學(xué)報,2015,30(4)：457-461.

[8] 屈婉玲,耿素云,張立昂.離散數(shù)學(xué)[M].北京：高等教育出版社,2012,1-150.

Calculating of the total number of T0-topologies on a 5-element set

RONG Yu-yin,XU Luo-shan
(Department of Mathematics,Yangzhou University,Yangzhou 225002,China)

Based on some results for fi nite posets and the specialization order of a topology,as well as relationships between topologies and orderings,we calculate the total number of T0-topologies on a 5-element set,which is 4231.We also calculate the total number of di ff erent topologies on a 5-element set,which is 6942.

fi nite poset;topology;minimal element;the total number of T0-topologies

54C35;06A11

O153.1;O189.1

A

：1000-4424(2016)04-0461-06

2016-01-30

2016-10-08

國家自然科學(xué)基金(11671008;61472343);江蘇省高校自然科學(xué)基金(15KJD110006);江蘇高校品牌專業(yè)建設(shè)工程項目(PPZY2015B109);揚州大學(xué)大學(xué)生學(xué)術(shù)科技創(chuàng)新基金