ON GROWTH OF MEROMORPHIC SOLUTIONS OF NONLINEAR DIFFERENCE EQUATIONS AND TWO CONJECTURES OF C.C.YANG?

Yueyang ZHANG(張月陽)Zongsheng GAO(高宗升)Jilong ZHANG(張繼龍)LMIB&School of Mathematics and Systems Science,Beihang University,Beijing 100191,China

?

ON GROWTH OF MEROMORPHIC SOLUTIONS OF NONLINEAR DIFFERENCE EQUATIONS AND TWO CONJECTURES OF C.C.YANG?

Yueyang ZHANG(張月陽)Zongsheng GAO(高宗升)Jilong ZHANG(張繼龍)
LMIB&School of Mathematics and Systems Science,Beihang University,Beijing 100191,China

E-mail:zhangyy8911@gmail.com;06712@buaa.edu.cn;09017@buaa.edu.cn

AbstractIn this paper,we investigate the growth of the meromorphic solutions of the following nonlinear di ff erence equations

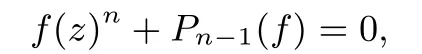
where n≥2 and Pn?1(f)is a di ff erence polynomial of degree at most n?1 in f with small functions as coeffi cients.Moreover,we give two examples to show that one conjecture proposed by Yang and Laine[2]does not hold in general if the hyper-order of f(z)is no less than 1.

Key wordsgrowth;meromorphic solutions;di ff erence equations;conjectures

2010 MR Subject Classi fi cation30D35;39A10

?Received October 27,2014;revised March 9,2015.The first author is supported by the NNSF of China(11171013,11371225,11201014),the YWF-14-SXXY-008 of Beihang University,and the Fundamental Research Funds for the Central University.

1 Introduction

In this paper,a meromorphic function always means meromorphic in the whole complex plane.We assume that the reader is familiar with the fundamental results and the standard notions of Nevanlinna’s value distribution theory of meromorphic functions(see,e.g.[1,4]).Let f(z)be a meromorphic function.We use σ(f)and λ(f)to denote the order of growth and the exponent of convergence of zeros of a meromorphic function f(z),respectively.In addition,we denote by S(r,f)any quantity that satisfies the condition S(r,f)=o(T(r,f))as r→∞outside of a possible exceptional set of finite logarithmic measure.A meromorphic function a(z)(∞)is called a small function with respect to f(z)provided that T(r,a(z))=S(r,f).Moreover,the hyper-order of growth of f(z)is de fined as follows

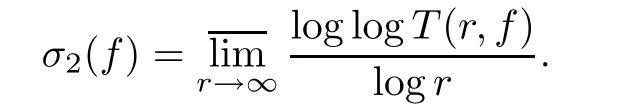
Recently,there was of Nevanlinna theory(see,e.g.,[5,6,8-10,12-17]).Given a meromorphic function f(z)and a constant c,f(z+c)is called a shift of f.As for a di ff erenceproduct,we mean a di ff erence monomial of typewhere c1,···,ckare complex constants,and n1,···,nkare natural numbers.In the following,a di ff erence polynomial,resp.a differential-di ff erence polynomial,in f is de fined as a finite sum of di ff erence products of f and its shifts,resp.of products of f,derivatives of f and of their shifts,with all the coeffi cients of these monomials being small functions of f.Yang and Laine[2]investigated the nonlinear differential-di ff erence equations and gave two conjectures on the nonexistence of entire solutions of in finite order to some differential-di ff erence equations.We now recall Theorem 2.4 in[2]and the two conjectures.

Theorem 1.1(see[2])Let p,q be polynomials.Then a nonlinear di ff erence equation

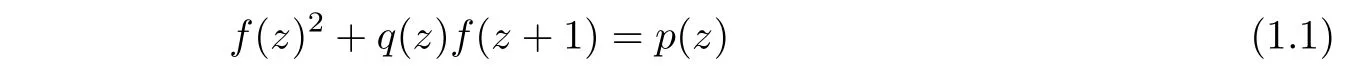
has no transcendental entire solutions of finite order.

Conjecture 1.2(see[2])There exists no entire function of in finite order that satisfies a di ff erence equation of type

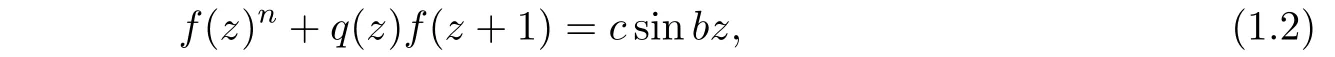
where q is a nonconstant polynomial,b,c are nonzero constants and n≥2 is an integer.

Conjecture 1.3(see[2])Let f be an entire function of in finite order and n≥2 be an integer.Then a differential-di ff erence polynomial of the form fn+Pn?1(z,f)cannot be a nonconstant entire function of finite order,here Pn?1(z,f)is a differential-di ff erence polynomial of total degree at most n?1 in f,its derivatives and its shifts,with entire functions of finite order as coeffi cients.Moreover,we assume that all terms of Pn?1(z,f)have total degree≥1.

Remark 1.4Li[3]proved that Conjecture 1.3 is correct when the hyper-order of f(z)is less than 1 by using a di ff erence analogue of the lemma on the logarithmic derivative(see[5,7])which was extended to the case of hyper-order σ2(f)＜1.

In this paper,we first investigate the following general nonlinear di ff erence equation

where n≥2 and Pn?1(f)is a di ff erence polynomial of degree at most n?1 in f.We mainly focus on the growth of the transcendental meromorphic solutions of(1.3)and give the following Theorem 1.5 and Theorem 1.6.

Theorem 1.5Suppose that f(z)is a transcendental meromorphic solution of(1.3),and Pn?1(f)is a di ff erence polynomial of degree at most n?1 in f.Then f(z)has in finite order.

Since all solutions of(1.3)is of in finite order,we now generalize Theorem 1.1 and estimate the hyper-order of the meromorphic solutions of(1.3)with rational coeffi cients.

Theorem 1.6Suppose that f(z)is a transcendental meromorphic solution of(1.3),and that all the coeffi cients of Pn?1(f)are rational,and that all the shifts of f(z)are f(z+c1),···,f(z+ck).Denote C=max{|c1|,···,|ck|}and

(1)If f(z)is entire or has finitely many poles,then there exist constants K＞0 and r0＞0 such that

holds for all r≥r0;

(2)If f(z)has in finitely many poles,then there exist constants K＞0 and r0＞0 such that

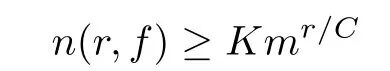
holds for all r≥r0.

Furthermore,we get σ2(f)≥1.

In Section 5,we will give two examples to show that Conjecture 1.3 does not hold in general if the hyper-order of f(z)is no less than 1.To Conjecture 1.2,we have the following conclusion.

Theorem 1.7Suppose that f(z)is an entire solution of in finite order satisfying(1.2).If σ2(f)＜∞,then for any entire function d(z)of finite order,we have λ(f?d)=∞.

2 Some Lemmas

Lemma 2.1(see[2])Let f(z)be a meromorphic function of finite order of a di ff erence equation of the form

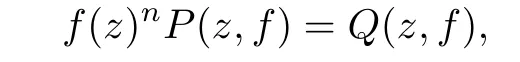
where P(z,f)and Q(z,f)are differential-di ff erence polynomials with all the coeffi cients aλ(z)being small functions of f(z)and degfQ(r,f)≤n.Then for each ε＞0,

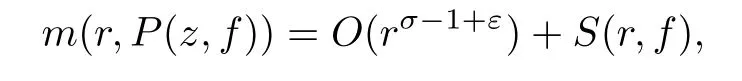
possibly outside of an exceptional set of finite logarithmic measure.

In what follows,a meromorphic function f(z)with more than S(r,f)poles(counting multiplicities)means that the integrated counting function of these poles is not of type S(r,f).

Lemma 2.2(see[14])Suppose that f(z)is a meromorphic solution of(1.3)with more than S(r,f)poles(counting multiplicities).We use∞k(0l)to denote a pole(zero)of f(z)with multiplicity k(l),and let zjdenote the zeros and poles of the coeffi cients ai(z)which are small meromorphic functions with respect to f(z).Let mjbe the maximum order of zeros and poles of the functions ai(z)at zj.Then for any ε＞0,there are at most S(r,f)points zjsuch that

where mj≥εkj.

Lemma 2.3(see[1])Let fj(z)(j=1,···,n)(n≥2)and gj(z)(j=1,···,n)(n≥1)be entire functions that satisfy

(2)when 1≤j＜k≤n,gj(z)?gk(z)is not a constant;

(3)when 1≤j≤n,1≤h＜k≤n,T(r,fj(z))=o{T(r,egk(z)?gh(z))}(r→∞,rE).Then fj(z)≡0(j=1,···,n).

The following lemma is more general than Theorem 1.45 in[1].By applying Theorem 1.4 in[1]and the Caratheodory’s inequality,we may easily get the conclusion,so we omit its proof.

Lemma 2.4Let h(z),a(z)be non-constant entire functions of finite order and f(z)= eh(z)+a(z).If h(z)is transcendental,then the hyper-order σ2(f)of f(z)satisfies σ2(f)=σ(h).

3 Proof of Theorem 1.5

ProofWe first observe that Pn?1(f)contains at least one shift of f(z),for otherwise(1.3)is obviously a contradiction.Let all the shifts of f(z)be f(z+c1),···,f(z+ck),where k∈N+,Now we suppose that f(z)is of finite order and we use the similar reasoning as that in the proof of Proposition 5.4 in[13].By Lemma 2.1,we conclude that m(r,f)=S(r,f).Therefore,N(r,f)=T(r,f)+S(r,f).Thus we may use the notations of Lemma 2.2 and say that f(z)has more than S(r,f)poles,counting multiplicities.Note that all the coeffi cients of(1.3)are of finite order.By the Hadamard’s theory,we may write a finite order meromorphic function a(z)as the formwhere p(z)is a polynomial and H1(z)and H2(z)(H1(z)H2(z)0)are the canonical products formed by the zeros and poles of a(z),respectively.Then we need write all the coeffi cients of(1.3)as the above form and multiply out all the denominators of the coeffi cients to obtain that

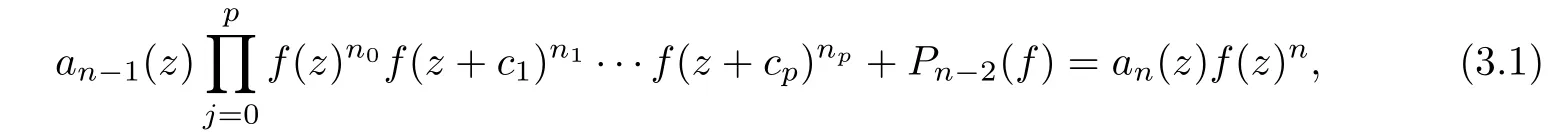
where n0+n1+···+np=n?1(p≤k),and that Pn?2(f)is a di ff erence polynomial of degree at most n?2 in f,and that all the coeffi cients of(3.1)are finite order entire functions.Denoting the points in the pole sequence of f(z)by zj,then we have f(zj)=∞kj.By Lemma 2.2,f(z)has more than S(r,f)poles so that we have mj＜εkjat zj,here mjrefers to the coeffi cients of(3.1).Let this sequence as our starting point and denote it by z1,j.Suppose that ε＜1,we see thatComparing this with the left-hand side of(3.1),we conclude that at least one of the terms of the left-hand side of(3.1)has a pole with multiplicitiesSince all the coeffi cients of(3.1)are entire functions,we see that there is at least one of the points z1,j+c1,···,z1,j+ckis a pole of f(z).In particular,we suppose that n0=0 and all z1,j+c1,···,z1,j+cpare such poles of f(z)with multiplicities k1,···,kpand that

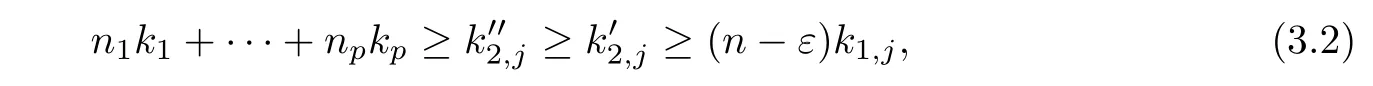
where n1+···+np=n?1.By taking ε＜1,we observe from(3.2)that at least one of k1,···,kp,say kμ,satisfies

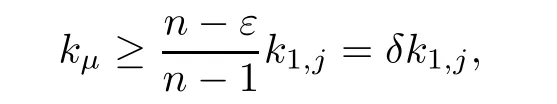
Then by induction,we may fi nally choose a sequence ziof poles of f(z)which satisfy the conditions f(zi)=∞kiand ki≥(δ)i?1k1≥(δ)i?1.We now estimate the counting functionN(r,f).Let C=max(|c1|,···,|ck|)and denote ri=|z1|+(i?1)C,then it is geometrically obvious that

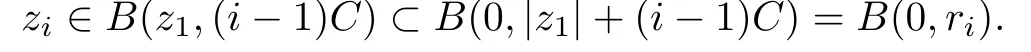
For i large enough,we have ri≤2(i?1)C,which suggests that

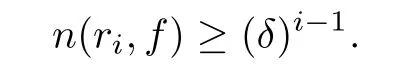
Hence,

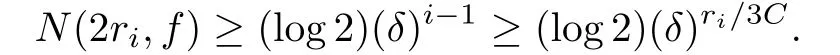
This means that f(z)is of in finite order,which obviously contradicts to our assumption that f(z)is of finite order and this completes the proof.

4 Proof of Theorem 1.6

ProofWe multiply out the denominators of the coeffi cients in(1.3)and write(1.3)as the following form

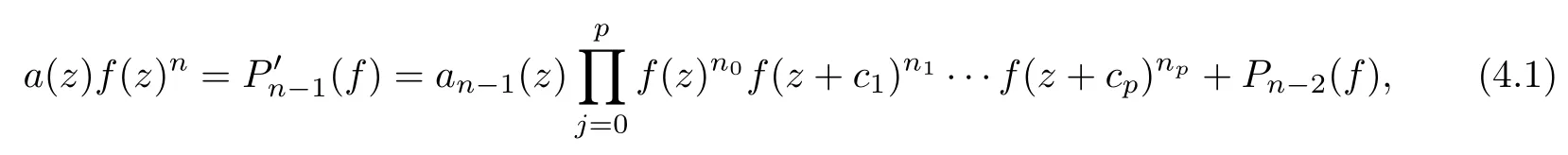
where n0+···+np=n?1,and that a(z)and an?1(z)are polynomials,and that Pn?2(f)is a di ff erence polynomial of degree at most n?2 in f with polynomial coeffi cients.The proof is now divided into two parts.

(1)Suppose that f(z)is a transcendental entire solution of(4.1).Let a(z)=as0zs0+···and denote the highest degree of the polynomials of(4.1)by s.We first have

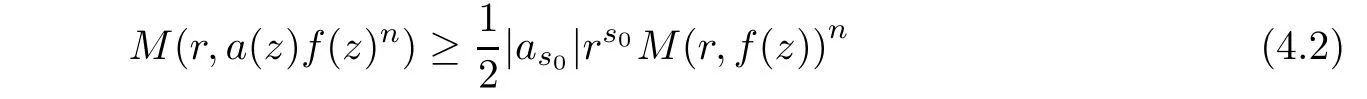
when r is large enough.The maximum modulus principle yields

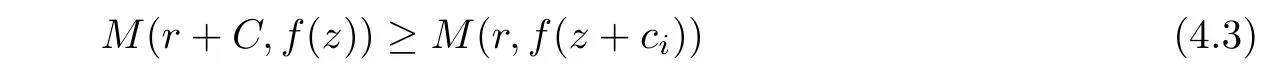
for all i=1,···,k.It follows from(4.1)-(4.3)that

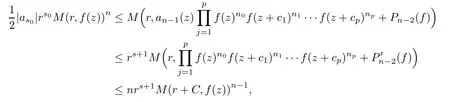
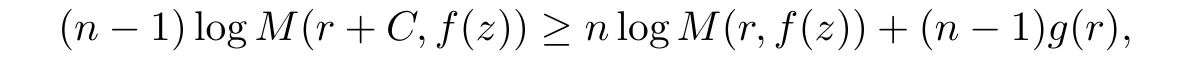
where g(r)＜K logr for some K＞0,when r is large enough.Sinceby iterating the above inequality,we have

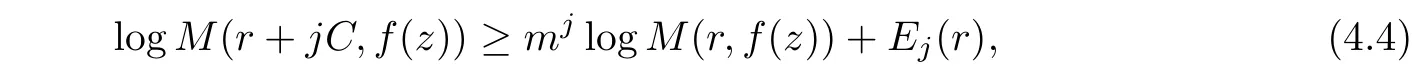
where

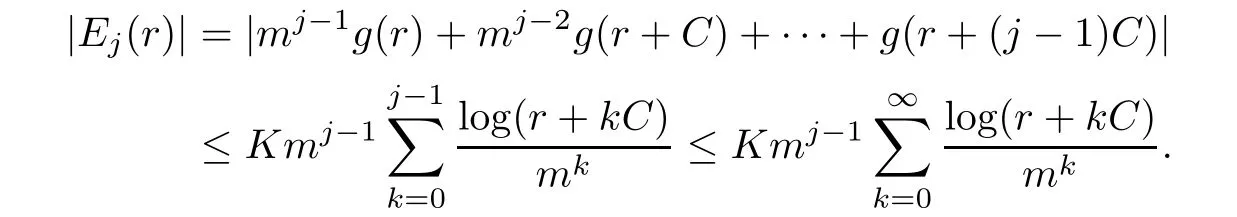
Since log(r+kC)≤logrlog(kC)for r and k sufficiently large,we observe that the series above converge wheneverHence

Since,by the hypothesis,f(z)is transcendental entire of in finite order,we have the inequality logM(r,f)≥2K′logr for r large enough.Thus(4.4)and(4.5)imply that

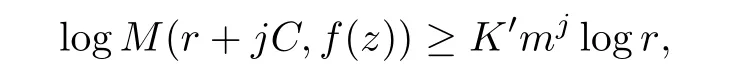
which holds for r sufficiently large,say r≥r0.By choosing r∈[r0,r0+C)arbitrarily and letting j→∞for each choice of r,we see that

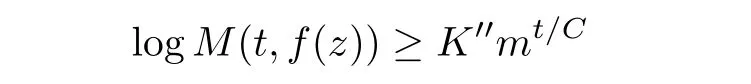
holds for all t≥t0:=r0+C,where K′′:=K′m?(r0+C)/Clogr0.We have proved the assertion in the case of f(z)being entire.

Suppose then that f(z)is meromorphic with finitely many poles.Then there exists a polynomial S(z)such that w(z)=S(z)f(z)is entire.Substituting f(z)=w(z)/S(z)into(4.1)and again multiplying away the denominators,we will obtain a di ff erence equation with polynomial coeffi cients similar to(4.1).Applying the reasoning above to w(z),we obtain,by the growth properties of polynomials,that

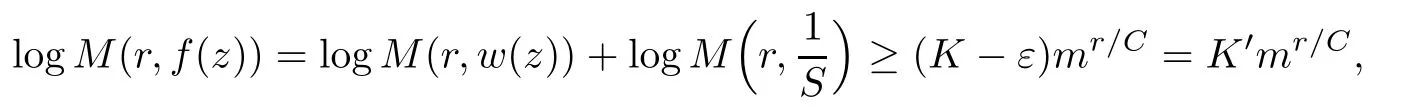
which holds for all r≥r1≥r0.We now prove the first part.

(2)Finally,we suppose that f(z)is meromorphic with in finitely many poles.Choose a pole z0of f(z)having multiplicity τ≥1 such that z0is not a zero of a(z).Then the left-hand side of(4.1)has a pole of multiplicity nτ at z0.Note that in this case we may let ε=0 in the proof of Theorem 1.5.Since all the coeffi cients of(4.1)are polynomials,then there is at least one of the points z0+c1,···,z0+ckis a pole of f(z)of multiplicityDenote one of these points by z0+ck1.Substitute z0+ck1for z into(4.1)to obtain

Since the coeffi cient a(z)has finitely many zeros only being inside of a finite disk|z|＜R and that f(z)has in finitely many poles,then by following the same processes as that in the proof of Theorem 10 in[12],we can obtain

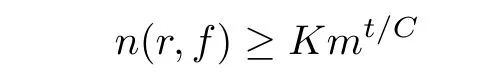
holds for all r≥r0:=(k0+1)C+|z0|,where k0is some positive constant and K:= τm?(r0+C)/C.The fact that r0and K both depend on|z0|is not a problem,since z0is fixed.

It is obvious that σ2(f)≥1,and this completes the proof.

5 Proof of Theorem 1.7 and Two Examples

ProofSuppose that λ(f?d)＜∞,then by Weierstrass’s theorem,f(z)has the form

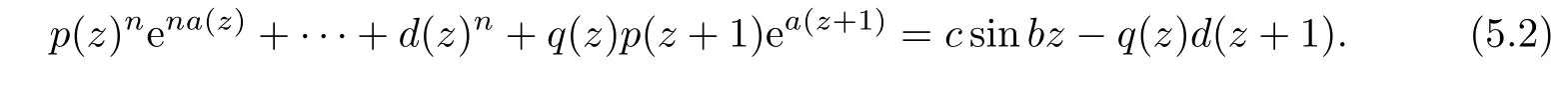
We then discuss the following two cases:

Case 1d(z)≡0.Then(5.2)can be written as

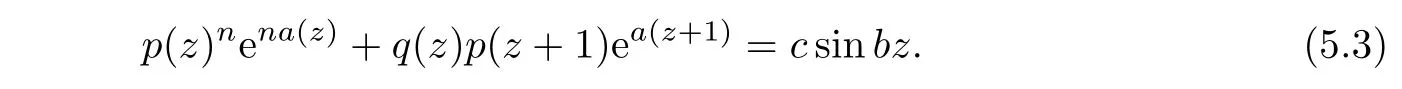
We claim that a(z+1)?na(z)is transcendental and satisfies σ(a(z+1)?na(z))=σ(a(z)).Otherwise,we may suppose that a(z+1)?na(z)is a polynomial or transcendental entire function and satisfies σ(a(z+1)?na(z))＜σ(a(z))and turn(5.3)into the following form

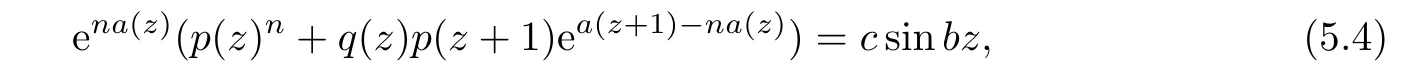
which yields a contradiction when comparing the order of growth of both sides of(5.4).Then by Lemma 2.3,we get from(5.3)that p(z)n≡0,a contradiction,and this leads to that λ(f)=∞.

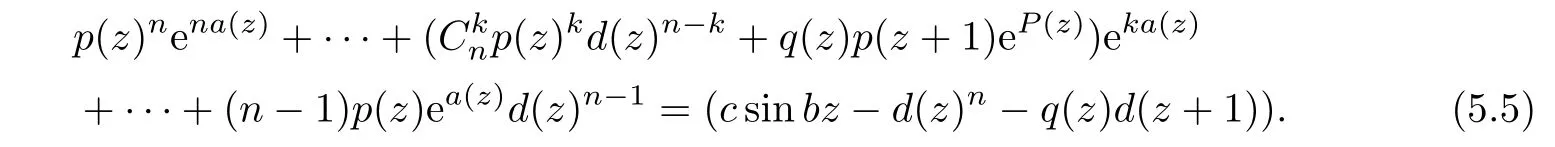
Since n≥2,then by Lemma 2.3,we can also obtain p(z)≡0 from(5.5),a contradiction again and this completes the proof.

Example 5.1Let f(z)=eez log 2+(log2)ez log 2.Then f(z)is of in finite order and satisfies the following equation

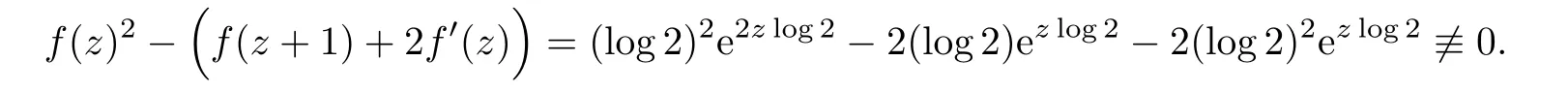
By Lemma 2.4,we know that σ2(f(z))=σ(ez log 2)=1.This example shows that Conjecture 1.3 does not hold in general when f(z)is of hyper-order σ2(f)=1.

We know from Theorem 1 in[11]that there exists a periodic function Π(z)with periodic 1 such that 1＜σ(Π(z))＜∞,thus we may give the following example.

Example 5.2Let f(z)=eg(z)+g′(z),and let g(z)=Π(z)ez log 2.Then we have σ(Π(z)ez log 2)＞1 and g(z+1)=2g(z).By Lemma 2.4,we know that σ2(f(z))=σ(Π(z)ez log 2)＞1.Now f(z)is of in finite order and satisfies the following equation

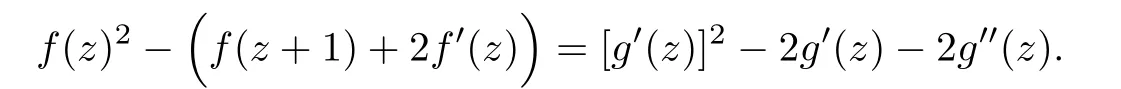
Let h(z)=g′(z),we have σ(h)=σ(g)＞1.Suppose that

then by Lemma 2.1,we have that m(r,h)=S(r,h),a contradiction to that h(z)is an entire function,which immediately gives

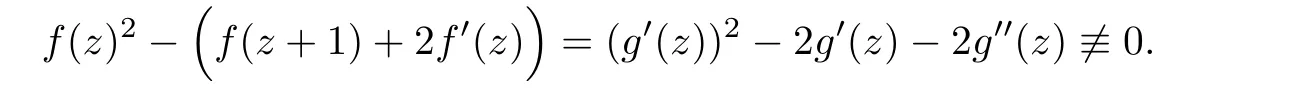
Thus we see that Conjecture 1.3 does not hold in general when f(z)is of hyper-order σ2(f)＞1.

References

[1]Yang C C,Yi H X.Uniqueness Theory of Meromorphic Function.Newtherlands:Kluwer Academic pulishers,2003

[2]Yang C C,Laine I.On analogies between nonlinear di ff erence and differential equations.Pro Japan Acad,2010,86(A):10-14

[3]Li N,Yang L.Some results related to complex linear and nolinear di ff erence equations.J Di ff Equ Appl,2014,20(2):237-250

[4]Laine I.Nevanlinna Theory and Complex Di ff erential Equations.Berlin:W de Gruyter,1993

[5]Halburd R G,Korhonen R J.Di ff erence analogue of the lemma on the logarithmic derivative with applications to di ff erence equation.J Math Anal Appl,2006,314(2):477-487

[6]Chiang Y-M,Feng S-J.On the Nevanlinna charactericstic of f(z+η)and di ff erence equations in the complex plane.Ramanujan J,2008,16(1):105-129

[7]Halburd R G,Korhonen R J.Holomorphic curves with shift-invatiant hyperplane preimages.arXiv:0903.3236v2

[8]Zhang J L,Gao Z S,Li S.Distribution of zeros and shared values of di ff erence operator.Ann Polon Math,2011,102:213-221

[9]Wen Z T,Heittokangas J,Laine I.Exponential polynomials as solutions of certain nonlinear di ff erence equations.Act Math Sinica,English Series,2012,66(2):1295-1306

[10]Chen Z X.On growth,zeros and poles of meromorphic solutions of linear and nonlinear di ff erence equations.Arch Math,2011,10:2123-2133

[11]Mitsuru Ozawa.On the existence of prime periodic entire functions.Kodai Math Sem Rep,1978,29(3):308-321

[12]Heittokangas J,Korhonen R,Laine I,Rieppo J,Tohge K.Complex di ff erence equations of Malmquist type.Comput Methods Funct Theory,2001,1(1):27-39

[13]Laine I,Yang C C.Clunie theorems for di ff erence and q-di ff erence polynomials.J Lond Math Soc,2007,76(3):556-566

[14]Halburd R G,Korhonen R J.Finite order solutions and the discrete Painlevé equations.Proc Lond Math Soc,2007,94:443-474

[15]Zhang J L,Korhonen R.On the Nevanlinna characteristic of f(qz)and its applications.J Math Anal Appl,2010,369(2):537-544

[16]Li S,Gao Z S.Resolts on a question of Zhang and Yang.Acta Math Sci,2012,32B(2):717-723

[17]Gao L Y.Estimates of n-functions and m-function of meromrophic sohctions of systems of complex di ff erence equations.Acta Math Sci,2012,32B(4):1495-1502