形式三角矩陣環(huán)上的F-Gorenstein平坦模

劉亞楠, 楊 剛

(蘭州交通大學(xué) 數(shù)理學(xué)院, 蘭州 730070)

1 引言及預(yù)備知識(shí)

左T-模的序列

T-Mod和A-Mod×B-Mod之間存在以下函子:

1)p:A-Mod×B-Mod→T-Mod, 對任意的對象(N1,N2)∈A-Mod×B-Mod, 令

對任意態(tài)射(f1,f2)∈A-Mod×B-Mod, 令

定義1[5]若對任意的平坦余撓模W, 函子HomR(-,W)作用序列F·仍得到正合序列, 則F·: …→F-1→F0→F1→F2→…稱為F-完全正合復(fù)形, 其中每個(gè)Fi都是平坦模.若存在F-完全正合復(fù)形F·, 使得M?Ker(F0→F1), 則稱左R-模M是F-Gorenstein平坦模.

引理3設(shè)M是R-模且n是整數(shù).若FGfdRM<∞, 則下列敘述等價(jià):

1)FGfdRM≤n;

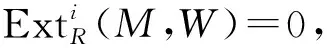
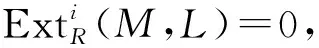
4) 對任意的正合列:

0→Kn→Gn-1→…→G0→M→0,

證明參見文獻(xiàn)[3]中定理4.5.

2 主要結(jié)果

下面給出形式三角矩陣環(huán)上的F-Gorenstein平坦模的結(jié)構(gòu)刻畫.

1)M1是F-Gorenstein平坦左A-模;

2) CokerφM是F-Gorenstein平坦左B-模;

3)φM是單射.

在這種情況下,U?AM1是F-Gorenstein平坦模當(dāng)且僅當(dāng)M2是F-Gorenstein平坦模.

證明: 必要性.M是F-Gorenstein平坦左T-模, 由定義1知, 存在平坦左T-模的正合列:

首先, 證明M1是F-Gorenstein平坦左A-模.由A·誘導(dǎo)的平坦左A-模的正合列為

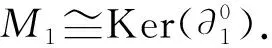
由于BU的平坦維數(shù)有限, 因此可假設(shè)fd(BU)=m<∞.由文獻(xiàn)[8]知, 對于任意的右B-模X, 有

最后, 證明CokerφM是F-Gorenstein平坦左B-模.考慮下列行正合的交換圖:

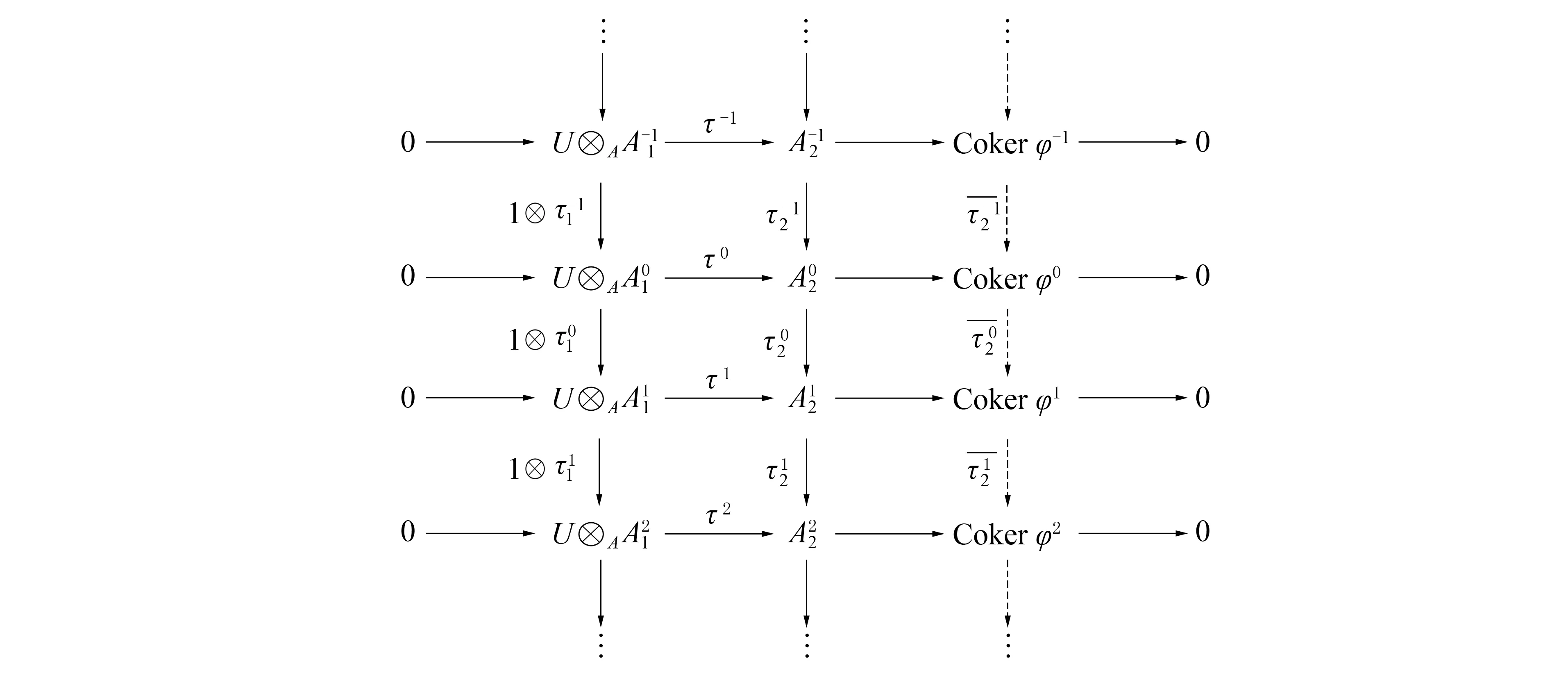
因?yàn)榈谝涣泻偷诙姓? 所以第三列正合.在上圖第0個(gè)位置取核, 得到正合列:

(1)

0→HomB(CokerφM,H)→HomB(M2,H)→HomB(U?AM1,H).

注意到

同理, 對任意的i∈, 有

因此序列

…→Cokerφ-1→Cokerφ0→Cokerφ1→Cokerφ2→…

函子HomB(-,H)作用正合.進(jìn)一步, 由定義1可知, CokerφM是F-Gorenstein平坦左B-模.

充分性.由φM是單射可知, 存在左T-模的正合列:

(2)

且對任意的i≥0, 有

由文獻(xiàn)[9]中引理3.2可知,

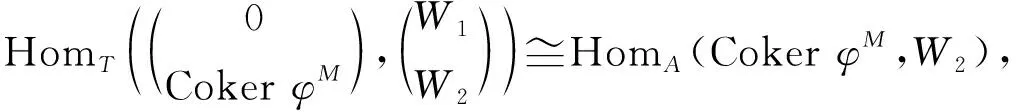
由于W2是平坦維數(shù)有限的余撓左B-模, 由文獻(xiàn)[9]中引理3.2和引理3知,

最后, 在上述情形下, 在左B-模的正合列

定理2設(shè)B是左凝聚環(huán).若BU是內(nèi)射模,UA是平坦模, 則對任意的左A-模X,U?AX是余撓左B-模.

證明: 對任意的左A-模X, 取X的平坦分解:

…→F2→F1→F0→X→0.

因?yàn)閁A是平坦模, 所以有正合列:

…→U?AF2→U?AF1→U?AF0→U?AX→0.

又BU是內(nèi)射模, 故由文獻(xiàn)[10]中定理3.2.16知,U?AFi是內(nèi)射左B-模.取U?AX的內(nèi)射分解:

則有下列余撓模的正合復(fù)形:

使得U?AX=Kerα.從而由文獻(xiàn)[6]引理1.1可知U?AX是余撓左B-模.證畢.

與定理1證明方法相同, 可得如下推論.

1)M1是F-Gorenstein平坦左A-模;

2) CokerφM是F-Gorenstein平坦左B-模;

3)φM是單射.

此時(shí),U?AM1是F-Gorenstein平坦模當(dāng)且僅當(dāng)M2是F-Gorenstein平坦模.

1)M是F-Gorenstein平坦左T模;

2)M1是F-Gorenstein平坦左R-模, CokerφM是F-Gorenstein平坦左R-模, 且φM是單射;

3)M2是F-Gorenstein平坦左R-模, CokerφM是F-Gorenstein平坦左R-模, 且φM是單射.

3 應(yīng) 用

1) 對任意的1≤i≤n,Mi是F-Gorenstein平坦左R-模;

2) 對任意的1≤i≤n-1, Cokerφi是F-Gorenstein平坦左R-模;

3) 對任意的1≤i≤n-1,φi:Mi→Mi+1是單射.

證明: 當(dāng)n=2時(shí), 由推論2可知結(jié)論成立.假設(shè)n>2, 并且結(jié)論對n-1成立, 下證結(jié)論對n成立.

(3)