Residual symmetries,consistent-Riccati-expansion integrability,and interaction solutions of a new(3+1)-dimensional generalized Kadomtsev-Petviashvili equation
Jian-Wen Wu(吳劍文), Yue-Jin Cai(蔡躍進(jìn)), and Ji Lin(林機(jī))
Department of Physics,Zhejiang Normal University,Jinhua 321004,China
Keywords: residual symmetry,interaction solutions,(3+1)-dimensional generalized Kadomtsev-Petviashvili equation
1. Introduction
As is known, nonlinear integrable evolution equations have been used in many nonlinear fields, such as fluid mechanics,[1-3]nonlinear optics,[4-6]plasma physics,[7,8]ferrimagnetics[9]and Bose-Einstein condensation.[10]A class of physically important integrable equations, such as the KP equation and the cubic gKP equation,has been applied to describe long wave propagation of small amplitude propagating in plasma physics[11,12]and the collapse of ultrashort spatiotemporal pulses in nonlinear optics.[13,14]In 1970,Kadomtsev and Petviashvili proposed the standard KP equation

For the new model, the Painlev′e integrability, bilinear form,multiple-soliton and lump solutions are investigated,while the interaction wave solutions are unsolved. It is well known that several systematic methods to construct exact and analytical solutions have been proposed, including inverse scattering method,[23,24]Hirota bilinear method,[25-30]and Lie group analysis.[31]The purpose of this paper stems from the observation of interaction waves in laboratory experiments,such as Fermionic quantum plasma[32]and elastic woodpile periodic structures.[33]In recent years, a number of papers have been devoted to research of interaction waves between solitons and other nonlinear waves.[34-36]Researchers have provided the nonlocal symmetry method,[37-42]the consistent tanh expansion method[43-45]and the consistent Riccati expansion(CRE)method,[46-50]which can be used to construct abundant interaction waves such as soliton-Painlev′e II waves and soliton-cnoidal waves. Based on the nonlocal symmetry method which is related to the infinitesimal forms of Darboux transformation and B¨acklund transformation(BT),many new interaction waves have been discussed for various integrable models,such as Korteweg-de Vries(KdV)equation,[51]sine-Gordon (sG) equation[52]and modified KdV-sG equation.[53]In addition, for the Painlev′e integrable systems, the interaction solution andn-th B¨acklund transformation has been obtained in Refs. [54-56]. Moreover, for some nonintegrable systems such as the Kraenkel-Manna-Merle system,the interaction waves can be constructed.[57]In this work,we employ the residual symmetries and the auto B¨acklund transformation of the gKP equation(3)to obtain analytic soliton-cnoidal wave solutions, which can describe a soliton moving on a cnoidal wave background.
The structure of the paper is as follows. In Section 2,we demonstrate the existence of the residual symmetry of the gKP equation(3)with the Painlev′e analysis. Then,we take advantage of introducing suitable auxiliary variables to construct the localization of the residual symmetry. Based on the results,we construct the finite symmetry transformation via solving the initial value problem. In Section 3, with the help of the CRE method we derive the CRE solvability for the gKP equation(3). In Section 4,some analytical soliton-cnoidal interaction solutions are studied in graphical way. Section 5 contains a conclusion and discussion.
2. Nonlocal symmetry of(3+1)-dimensional gKP equation



Here,{u,f,g,h}is a solution of the prolonged system (11),and another solution{ˉu,ˉf,ˉg,ˉh}can be obtained by the finite symmetry transformation(16).
3. CRE solvability of the(3+1)-dimensional gKP equation
In this section, based on the CRE method, we prove the CRE solvability of the gKP equation (3). Using the leading order analysis,we can realize that the truncated solution of the gKP equation(3)reads

4. Soliton-cnoidal wave solutions
In this section, the solutions of the (3+1)-dimensional gKP equation will be obtained, including trivial straight-line solutions and soliton-cnoidal wave solutions. As we all know,a trivial straight-line solution is formed as

It is very interesting that the interaction solutions between soliton and cnoidal wave are displayed in the Fermionic quantum plasma.[32]Consequently,to seek out the soliton-cnoidal wave solutions,one can assumeφin the following form:



in the plane (x,z) and the plane (y,z). Figures 1(c) and 1(d)clearly display the wave travel mode along theyandzaxes,respectively. The type of interaction solution can describe the soliton scattering from cnoidal wave train in a fiber.[62]

Fig.1. The type of a bright soliton on a cnoidal wave background expressed by Eq.(30)with Eq.(31):(a)the corresponding three-dimensional plot of the soliton-cnoidal wave in the plane(x,z)at t=0,(b)the three-dimensional plot of the soliton-cnoidal wave in the plane(y,z)at t=0,(c)the wave travel mode along the y axis,(d)the wave travel mode along the z axis.

where

with the arbitrary constantsk1,k2,l1,l2,ω1,ω2,m2,βandγ. Meanwhile, the constantsm1andmare given by Eq.(33),and sn =JacobiSN(k2x+l2y+m2z+ω2t,m),cn =JacobiCN(k2x+l2y+m2z+ω2t,m)and dn=JacobiDN(k2x+l2y+m2z+ω2t,m). From Fig.(2),we find that one soliton resides on the cnoidal wave instead of plane wave background by choosing suitable coefficients

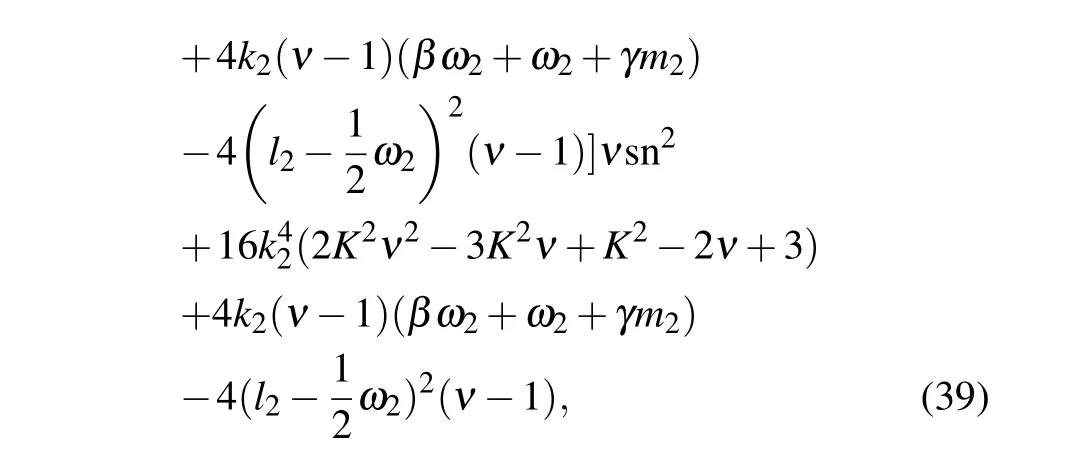
with the functions sn = JacobiSN(Kξ,m), cn =JacobiCN(Kξ,m), dn =JacobiDN(Kξ,m). This kind of interaction solutions is more useful in plasmas.[32]
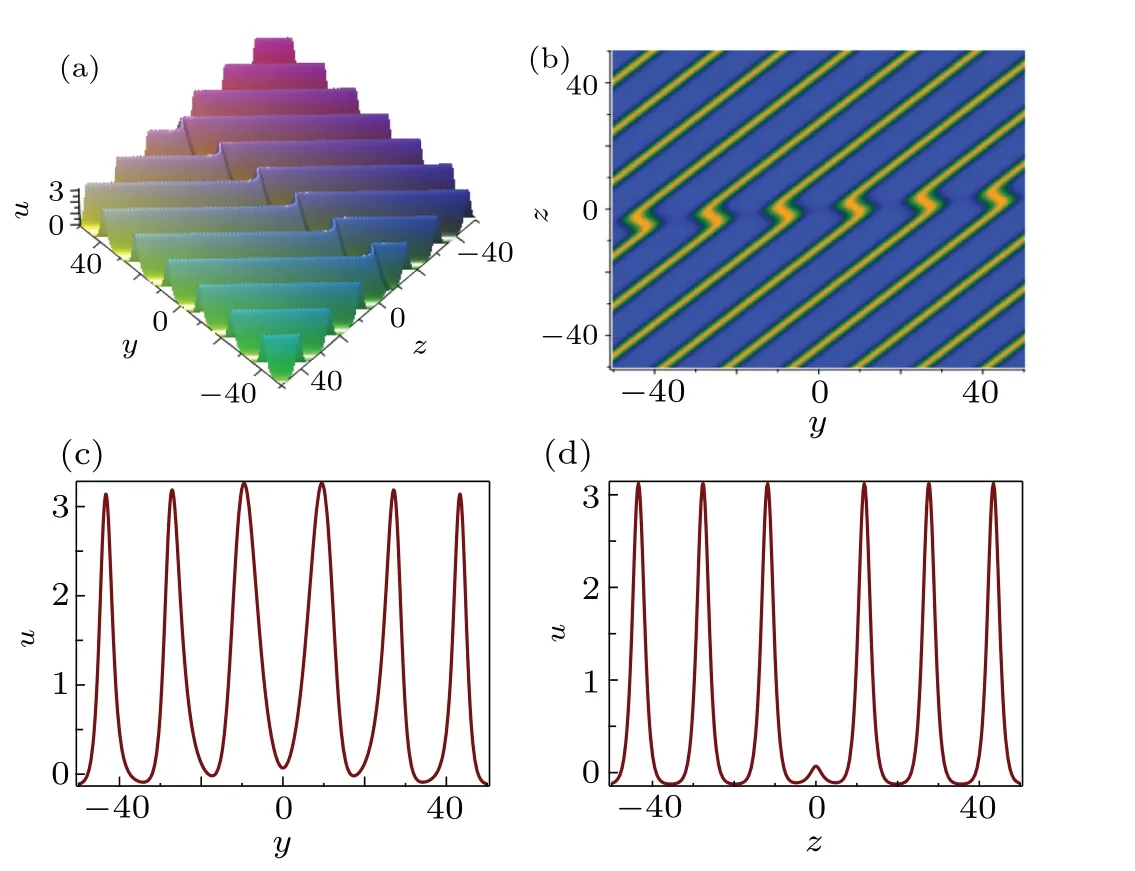
Fig.2.The type of a soliton resides on a cnoidal wave background expressed by Eq.(34)with Eqs.(33)and(36):(a)the corresponding three-dimensional plots for components u in the plane(y,z)at t=0,(b)the density plot of the soliton-cnoidal wave in the plane (y,z) at t =0, (c) the wave travel mode along the y axis,(d)the wave travel mode along the z axis.
5. Conclusion and discussion
In conclusion, the interaction waves of the 3+1-dimensional gKP equation(3)are studied via its residual symmetries related to its Painlev′e integrability. Firstly, a special residual symmetry is constructed for the gKP equation(3)by requiring the prolong system(11). Then,due to Lie’s first fundamental theorem, the initial value problem has been solved,which leads to a finite symmetry transformation,and with the help of the finite symmetry transformation,one can find some new solutions of the gKP equation(3)from a given one. Furthermore,according to the CRE method,the consistent equation(20)of the gKP equation(3)is obtained.Finally,the interaction solutions for soliton-cnoidal wave are unearthed,which can be explicitly constructed by the Jacobi elliptic functions.
It would be very interesting to search for nonlocal symmetries in any other integrable systems. There are other more methods to obtain the nonlocal symmetries, such as the Darboux transformation[59]and the B¨acklund transformation.[37]Many questions remain open in the domain of interaction solutions among different waves, which need be investigated in the future.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(Grant Nos.11835011 and 12074343).
- Chinese Physics B的其它文章
- Surface modulation of halide perovskite films for efficient and stable solar cells
- Graphene-based heterojunction for enhanced photodetectors
- Lithium ion batteries cathode material: V2O5
- A review on 3d transition metal dilute magnetic REIn3 intermetallic compounds
- Charge transfer modification of inverted planar perovskite solar cells by NiOx/Sr:NiOx bilayer hole transport layer
- A low-cost invasive microwave ablation antenna with a directional heating pattern

