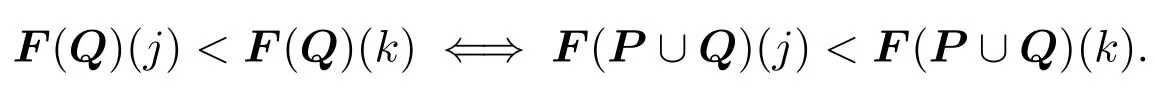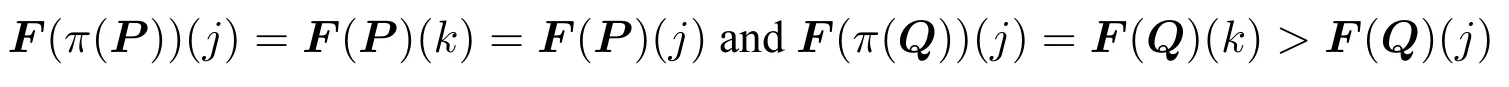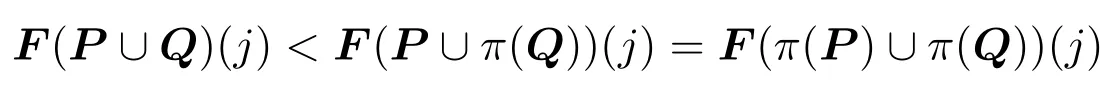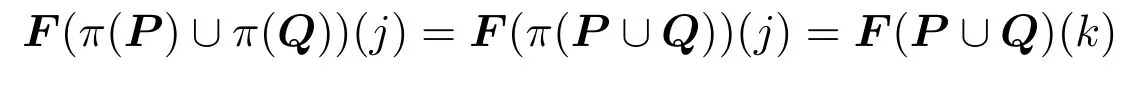一個(gè)真值函項(xiàng)偶然邏輯的希爾伯特演算系統(tǒng)
梁 飛 田中旭 楊新宇
1 Introduction
The study of voting systems,as an important part of social choice theory,formulates how a group should choose the winner(s) from among several alternatives.As the analysis in[20],a voting system should consist of two parts:a balloting procedure to state what information the voters are supposed to write on the ballots,and an aggregation procedure to state how to aggregate the voted ballots into a collective decision.
The most common voting system is plurality voting,where each voter can write down his/her favorite option only and the alternative favored by most voters would be the winner.When there are just two alternatives,plurality voting is equivalent to the majority rule,which is finely justified by May’s theorem ([18]) and widely accepted for binary decisions in practice.However,for elections with more than two alternatives,plurality voting suffers from the spoiler effect,which refers to an alternative who itself has no chance to win but could change the outcome by joining in the election.1A vivid illustration of the spoiler effect can be found in[23].This highlights the fact that plurality voting has no information about the voters’preferences besides their favorite options.
The classical design of the balloting procedure is asking each voter to rank all alternatives into a linear order.It provides more possibilities for the design of aggregation procedure since more information has been collected.The systems built in this way,such as Condorcet method,Borda count,and instant-runoff voting are all called rank-order systems.K.J.Arrow developed a method to study rank-order systems within an axiomatic framework,and yet obtained a negative conclusion——Arrow’s impossibility theorem.([1])In that pioneering work,he introduced three reasonable axioms and proved that they are incompatible whenever there are more than two alternatives.Basically,Arrow’s theorem tells us that no rank-order system is qualified to be an ideal voting system.
Afterwards,scholars gradually turned attention to another kind of balloting procedure,which allows each voter to evaluate alternatives individually.The allowed valuations are usually in the form of numbers and should be fixed beforehand.Meanwhile,the aggregation procedure is simply defined as an addition or averaging operation,which outputs a score for each alternative.We call systems of this kind scoring rules.As a result,the central issue of scoring rules is about choosing an appropriate set as the range of allowed valuations.Note that voters could select valuations from the appointed set freely.2For this reason,neither the point system in [27] nor the scoring function in [30] belongs to the scoring rules we are talking about here.Instead,they are variations of Borda count and still belong to rank-order systems.Then,they could express preferences with intensities when that set is large enough,which should be an advantage over rank-order systems from the informational perspective.Hence we prefer to choose an infinite set and there are two common options:R or[0,1].
The formal utilitarian voting has chosen R and interprets the valuations as utilities or welfare of voters.Different axiomatic characterizations of it can be found in[9,15,22].For the discussion of utilitarianism in economics,see[4,7,11,10,24,25].While some others proposed to normalize the utility into the set[0,1]and obtained relative utilitarianism.([5])It presupposes that all the voters are strategic,so each voter’s maximal and minimal valuations under formal utilitarianism are transformed to 1 and 0 respectively,and then the others into(0,1)in proportion.By contrast,range voting,another scoring rule that has chosen[0,1]as the set of allowed valuations,does not have any such presuppositions.Range voting is strongly advocated by W.D.Smith([28,29]),and has already had several axiomatic characterizations([9,16,21,22]).
This paper aims to justify range voting by replenishing an explicit semantical interpretation,without which we have no reasonable grounds for performing the aggregation procedure.Unlike relative utilitarianism,we regard one valuation as the degree of voter’s satisfaction in the absolute sense.Moreover,we suggest collecting another kind of information,the qualitative judgement,to know whether one voter approves an alternative or not.This information is concerned by the approval voting([3]) and D.S.Felsenthal divided it into three types:approval,disapproval and vacancy([6]).To highlight the differences from relative utilitarianism,we still choose the set[0,1]instead of[?1,1]and let 0.5 indicate the vacancy of opinion.Therefore,all the valuations higher than 0.5 mean approval and the others disapproval.In particular,1 means an alternative is absolutely perfect for a voter and 0 means the opposite.All of these statements should be acknowledged by voters.
Next in section 2,we construct a framework for formulating elections.Section 3 shows some commom axioms and clarifies two kinds of definitions.Also,by virtue of the qualitative judgement,we introduce a new axiom called Neutralization of Attitude.The main result of this paper,an axiomatization of range voting,is obtained in section 4.Section 5 improves the system by introducing two conditions and section 6 comes to the conlusion part.
2 Preliminaries
There are five things we should make clear:voters,alternatives,the desired outcome,balloting procedure and aggregation procedure.Usually,both the numbers of voters and alternatives are fixed for formulating a voting system.However,considering that sometimes we need to aggregate the ballots separately and combine the outcomes later,a voting system should be able to handle elections with variable numbers of voters and satisfy some kind of“consistency”with respect to the combination.J.Smith introduced an axiom named separability in[27]to describe this property,and as he emphasized in the title,his procedure works with“variable electorate”.Similar or equal axioms have been defined by others,e.g.,elimination in[7],consistency in [30] and reinforcement in [19].3It might be confusing that these axioms were not named in a unified way.For instance,the separability in[4,24]are different with that in[27],but almost equal to the elimination in[7].Following this approach,we also define voting systems for variable voters.
LetXdenote the set of all alternatives and supposecard(X)≥3.The desired outcome of an election includes how many winners there should be and whether the order of winners matters.In this paper,we focus on the single-winner elections as many others do since the procedures could be applied to plural-winner elections by selecting alternatives one by one.Though others may insist that the combinations of alternatives should be taken into consideration in plural-winner elections([2]),we can handle this issue by a modification onX.To be specific,if the order of winners matters such as selecting two alternatives to be the president and the vice president,the set for voters to estimate should beX′{(a,b)|a,b ∈Xandab}?X×X,whereaandbdenote those two positions respectively.Then,a plural-winner election onXbecomes a single-winner election onX′.
The balloting procedure is that we proposed in the Section 1.Let∈Vbe the voteri’s valuation on alternativej,whereV{vis a real number|0≤v ≤1}.In particular,0(1)indicates thatjis the worst(best)alternativeicould imagine,and0.5 means thatihas little knowledge aboutjand he/she is neutral forjto be the winner.LetPi∈V mbe the voteri’s valuation onX,then we can get a profilePn∈(V m)nby collectingnvoters’valuations in order.Finally,we define the aggregation procedure as follows:
Definition 1(Aggregation Procedure) An aggregation procedureFis a group of social scoring functions such that,for any numbern,there exists a uniquen-ary social scoring functionFn:(V m)n →V mwhich takes any given profilePntoFn(Pn)as the collective valuationF(Pn).4The superscript n can be omitted when it is obvious or unimportant.
LetFn(Pn)(j)orF(Pn)(j)denote the collective valuation on alternativej.
3 Basic Axioms
SinceFis a scoring system,it provides a new way to define some axioms by concerning the scores of alternatives rather than the order of them.However,these two kinds of definitions have not been explicitly distinguished so far and many authors still prefer to concern the ordering due to two main reasons:(1) Usually,the order-concerned definitions state weaker requirements onFthan the score-concerned definitions do;(2)It is the order of alternatives instead of the scores of them that essentially decides the winner.To clarify this distinction,we show both kinds of definitons for some axioms and mark the score-concerned one with a star symbol*.
First,all of the voters should be treated equally,i.e.,their names are insignificant information for the election.This sort of equality can be defined as the axiom of anonymity([2,30]):
Axiom 1 Anonymity(A).For any profilesPandQif there exists a permutationσofN{1,2,···,n}such thatfor allx ∈N,then we haveF(Q)F(P).
The profileQcan be obtained fromPvia a permutation among voters’valuations,which regardsas the voteriσ(x)’s valuation.Axiom(A)states that the permutation should not make any difference to the outcome.
Similarly,the equality among alternatives leads to an axiom called neutrality.5The combination of anonymity and neutrality is exactly the symmetry in[30].It requires that any permutation among alternatives should cause the same permutation of the outcome.
Axiom 2 Neutrality(N*).For any profileP(Pi1,···,Pin)and any permuationπofX,letπ(P),···,πwherethen for allj ∈X,we haveF(P)(π(j))F(π(P))(j).
The profileπ(P) is obtained by regarding the valuations onπ(j) as valuations onjfor all alternativesj.Axiom (N*) requires that the permutation of the outcome preserves the scores of alternatives,while the classical order-concerned definiton of neutrality makes a weaker requirement that only the ordering of alternatives needs preserving.
Fshould be provided with the independence of irrelevant information,the two kinds of definitions are as follows:
Axiom 3
?Unary Independence of Irrelevant Alternatives(UIIA*).For any profilesPn,and anyj ∈Xsuch thatfor all votersi,we haveF(Pn)(j)
?Binary Independence of Irrelevant Alternatives (BIIA).For any profilesPn,and anyj,k ∈Xsuch thatfor all votersi,we have thatF(Pn)(j) The principle of axiom(UIIA*)is that the voters’valuations on others are irrelevant information for deciding one alternative’s final score.It was named localization in[15].Axiom(BIIA)states that the order of any two alternatives should be completely decided based on the valuations they have got.([16])It would be easy to check that(BIIA)could be derived from(UIIA*). When all the voters hold identical opinions on an issue,Fshould keep this opinion through the aggregation.This property is defined as the axiom of unanimity: Axiom 4 ?Unanimity(U*).For any profilePand anyj ∈X,ifa ∈Vfor all votersi,then we haveF(P)(j)a. ?Unanimity(U).For any profilePand anyj,k ∈X,iffor all votersi,then we haveF(P)(j) Axiom(U)states that if all of the voters strictly prefer one alternative to another,so should the collective decision.It was adopted in[1]and called weak Pareto principle in[8,p.20].Thestrong Pareto principle(SP)has a weaker premise:If there exists a subgroup of voters who strictly prefer one alternative to another,so should the collective decision as long as none of the others strictly prefers the latter alternative.([4,7,16])Others have different names for SP,such as:positivity in[14],individualism in[13]and monotonicity in[9].Axiom(U*)states a unanimity with respect to one alternative’s score.When all the voters give the same valuations on an alternative,Fhas no reason to assign another value to that alternative,especially considering that each value has a semantical interpretation in our system.Notice that neither of axiom(U)and(U*)could imply the other one. Also,there are different invariance axioms about transformations of profiles,which depend on the stance to be taken towards interpersonal comparability.The distinction of different approaches for interpersonal comparisons was first introduced by A.K.Sen in[26,Ch.7],and it was adopted by others later.Among all these invariance axioms,full comparability(FC)is the weakest one([24,17]),and it was named co-cardinal(CC)in[12,4,10].In this paper,we take the view that the valuations of different voters are fully comparable and introduce an axiom even weaker than FC: Axiom 5 Ordinal Invariance under Isometry(OII).For any profilesPn,,if there exists a real numberasuch that for alliandj,+a,then for allj,k ∈X,we haveF(Pn)(j) Note thatPn,are proper profiles and the value of numberais fixed accordingly.The intuition of axiom(OII)is:when a profile can be obtained from another one after increasing/decreasing all the valuations by the same number,Fshould keep the ordering of alternatives unchanged since no alternative has gained advantage over others in the process.This axiom can be regarded as a simplified version of the axiom translation-invariance(TI)in[15],which allows more complex translations and equipped with(BIIA)inherently.We have a direct corollary of(OII): Corollary 1For any profilesPn,,if there exists a real numberasuch that for alliandj,+a,then for allj,k ∈X,we haveF(Pn)(j)F(Pn)(k)??F(Pn)(k). To make sure thatFis internally a coherent procedure,there are axioms that describe the relations among the functions inF.Usually,these axioms are formulated as howFshould combine the decisions of two seperate groups into a final decision,as mentioned in Section 2.For simplicity,from now on we assmue thatFsatisfies axiom (A),then we can arrange a profile in any way as needed.LetP∪Qdenote the profile combined from profilesPandQ,whereP∈(V m)nandQ∈(V m)r. When a subgroup of voters varies their collective valuation,Fshould be sensitive to the variation and always give positive response in the outcome.This property is defined as the axiom of monotonicity6Though monotonicity is a typical score-concerned definition,there is an axiom named(EIG)which can be regarded as the order-concerned version of monotonicity,see explanation in the appendix part.: Axiom 6 Monotonicity(Mon).For any profilesP,Qn,and anyj ∈X,we have Note that axiom(Mon)has no requirement about how the individuals in that subgroup changed their opinions.With the help of axiom (A),we have a corollary of (Mon)immediately: Corollary 2For any profilesPl,and anyj ∈X,we have Moreover,ifFsatisfies both axiom(A)and(U*),we have another corollary of(Mon):Corollary 3For any profilesPl,Qnand anyj ∈X,ifF(Pl)(j) Coro.3 says that one alternative’s final score after a combination of two profiles should remain between its two scores before.It can be interpreted as a two-way monotonic property and fits well with our intuition. Notice that each voter can be regarded as a group with only one member,by axiom(U*)we haveF(Pi)Pifor any voteri.Then it would be easy to check that the(UIIA*)is included in Coro.2.We conclude these into a lemma: Lemma 1(A)+(U*)+(Mon)?(UIIA*). When there are two groups of voters of equal number that hold opposite opinions on an alternative with equal intensity,Fshould not take any side of them,i.e.,the collective valuation of all these voters on that alternative should be neutral.Borrowing the idea of neutralization reaction in chemistry,we call this property neutralization of attitude. Axiom 7 Neutralization of Attitude(NA).For any profilesPn,Qnand anyj ∈X,we haveF(Pn)(j)+F(Qn)(j)1?F(Pn∪Qn)(j)0.5. Axiom 8 Reverse Neutralization of Attitude (RNA).For any profilesPn,Qnand anyj ∈X,we haveF(Pn∪Qn)(j)0.5?F(Pn)(j)+F(Qn)(j)1.By virtue of axiom(A),the axiom(RNA)states that if a group of voters has a neutral valuation on an alternative,any fifty-fifty division of this group,if possible,would result in two subgroups which hold opposite opinions on that alternative with equal intensity.The following theorem gives the connection between(NA)and(RNA): Theorem 1.Given axioms(U*)and(Mon),we have(NA)?(RNA). Definition 2(Range Voting) Range voting is an aggregation procedureAsuch that for any profilePnand anyj ∈X, Theorem 2.The range votingAis the unique aggregation procedureFwhich satisfies axioms(A),(U*),(OII),(Mon),and(NA). ProofIt is obvious thatAsatisfies all these axioms,we prove the other direction only.SupposeFis an aggregation procedure which satisfies all five axioms above,thenFalso satisfies Coro.1,2 and(UIIA*)(by Lem.1). We inductively prove that for alln,F(Pn)(j)(1≤s ≤n),wherePn,jare arbitrary. ? Base step: Letkbe another alternative andQ,∈P2be two profiels such thatis obtained by an enhancement fromQin the distance ofd.In particular,the valuations onj,kare as follows: (2.3)a+b>1,similar to(2.2). ? Induction step: (3) Suppose the proposition holds for alln ≤2z,then (3.2)n2z+1. Then the proposition holds for alln ≤(2z+2). Now we have proved thatF(Pn)(j)(1≤s ≤n)for alln,which meansFis exactly the range votingA. □ Compared with rank-order systems,scoring rules not only distinguish alternatives from good to bad but also have separate valuations for each of them.In range voting,one alternative’s final score indicates how satisfied the whole group of voters would be if it wins the election.Then the ties among several alternatives could be broken randomly since voters are indifferent to them.Moreover,the information of qualitative judgement puts forward a requirement for the winner: Condition 1Ifjis the winner of an election,thenF(P)(j)>0.5. This condition states that the winner should be approved by the group of voters.Note that the threshold value must also be 0.5.Otherwise,by axiom(U*),there would be an alternative who is approved by each voter but disapproved by the whole group or vice versa. When no alternatives could satisfy the Condition 1,voters have rights to reject all of them and reorganize an election by nominating new alternatives if possible.So our system can prevent the situations where voters have to choose the best one from incompetent alternatives,or in other words,choose the lesser of several evils.This kind of collective veto is a merit that no other systems have.Also,it should not be regarded as a violation of the default axiom ofuniversal domain([8])since the rights of veto did not damage the system’s capability of selecting the best one,regardless whether or not it is approved by the group. One forceful attack on scoring rules is that they could cause a result against the will of the majority.It is conceivable that one alternative preferred to another one by most voters could have lower final score than that one in range voting.Would that be acceptable? First,we have a discussion about Condorcet method,which is a productive attempt of applying majority rule to the elections of multiple alternatives.It checks out the voters’preferences between each pair of alternatives with the majority rule,and select the one who has an advantage over each others as the Condorcet winner.Though Condorcet method is reasonable enough,the only defect is that it violates the axiom of universal domain because the Condorcet winner does not always exist.Sometimes,there might be a cyclic structure formed by three or more alternatives,within which each alternative is dominated by another one,in which case selecting a winner from them would unavoidably violate the majority rule.So,the majority rule itself is not a consistent principle for elections of multiple alternatives and the violation of it seems not to be an effective charge. The problem truly bothers here is that a Condorcet winner,though regarded as a perfect candidate in general view,could still be defeated in scoring rules.However,as we emphasized in Section 1,the information scoring rules have taken into consideration are not just about preference but also the intensity of preference.In range voting,an alternative can defeat a Condorcet winner only if its supporters in the minority support it with much more intensities.So,roughly speaking,range voting could avoid delighting most voters by tremendously sacrificing the happiness of the others,while majority rule lacks this very kind of protection for the minority.On the other hand,range voting also has a tendency to slightly sacrifice most voters for great improvments of a few others.The following condition set a limit for this tendency so that the majority would not be disappointed too much:Condition 2Ifjis the winner of an election,then This condition could make sure that the winner is at least an acceptable option for most voters.Then we can accept the violation of majority as a necessary compromise for employing scoring rules. In summary,condition 1 and 2 provide criteria for voters to review the alternatives after aggregation procedure.Alegitimate winneris the alternative who has highest final score and satisfy both conditions above.An election without such legitimate winner should be marked with“unsuccessful”and the alternative with highest final score could be a temporary winner.The voters have rights to reorganize a new election whenever possible.In this sense,we say that the system of range voting is improved by condition 1 and 2. One novelty of this paper is provding an explicit semantical interpretation for range voting,which includes the information of qualitative judgement and regards the valuation as the degree of voters’satisfaction in the absolute sense.By virtue of this interpretation,we defined a new axiom named NA to handle valuations of opposite judgements and an interesing corollary of it named RNA.Also,the interpretation enabled us to define two conditions to be applied after aggregation.The alternative who has highest score among those who satisfiy both conditions would be a legitimate winner in our system.This additional procedure to review the alternatives could give voters a better estimation of the ongoing election,which is an advantage over other systems without qualitative judgement. Another effort is clarifying two kinds of definitions of axioms in this literature.In accordance with the distinction between rank-order systems and scoring rules,the common axioms were classified into order-concerned and score-concerned definitions in section 3.Then we got to survey these axioms from an overall perspective and rename some axioms to unveil the relations among them. The main result of this paper is an axiomatic characterization of range voting which includes five axioms:(A),(U*),(OII),(Mon),and (NA).That constitutes a mathematical justification for our system,while the conditions 1 and 2 in section 5 improve the system from procedural perspective. Appendix Proof of Corollary 3SupposeF(Pl)(j)a Proof of Theorem 1Suppose not,then there are profilesPn,Qnsuch thatF(Pn∪Qn)(j)0.5 andF(Pn)(j)+F(Qn)(j)1.AssumeF(Pn)(j)a,F(Qn)(j)banda+b<1.Letbe a profile such that1?afor all votersi,then by(U*)we haveF1?a.Then by(NA)we haveF(Pn∪0.5 sinceF(Pn)(j)+F(j)1.But by(Mon)we haveF(Pn∪>F(Pn∪Qn)0.5 since 1?a >b.Contradiction! Similarly,it can not be the case thata+b >1.Then we are done. □ Axiom 9 Elimination of Indifferent Group(EIG).For any profilesP,Qand anyj,k ∈Xsuch thatF(P)(j)F(P)(k),we have The original idea of axiom(EIG)is:when a subgroup of voters are indifferent to two alternatives,this subgroup could be eliminated without changing the order of those two alternatives.([7])The separability in[4,24]can be regarded as elimination of indifferent individuals instead of subgroup. However,we can give another explanation for(EIG).Instead of considering the effectPhave onQ,we can see thatFgive positive response on the issue ofjversuskwhen an indifferent profilePwas combined with another profileQ.In this sense,(EIG)is monotonic with respect to ordering and can be regared as the order-concerned version of(Mon).We prove a theorem to demonstrate this relation: Theorem 3.Given axiom(N*)and(A),we have(Mon)?(EIG). ProofGiven two profilesP,Qand two alternativesj,k ∈Xsuch thatF(P)(j)F(P)(k)andF(Q)(j) By(Mon)and(A)we have And by(N*)we have Then we come to the conclusion thatF(P∪Q)(j)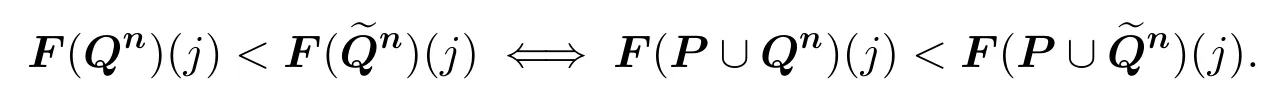
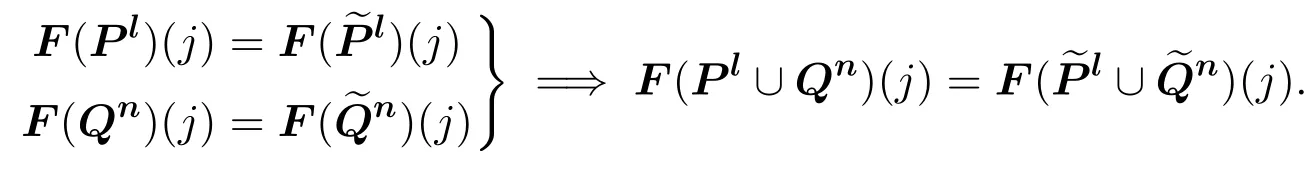
4 Axiomatic Characterization of Range Voting
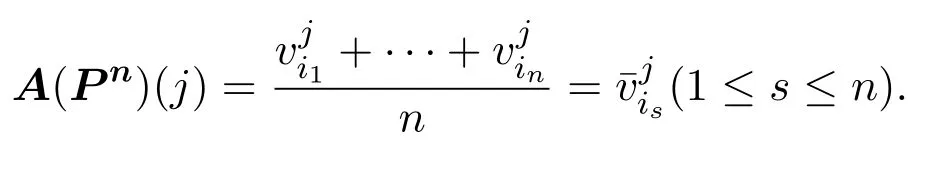

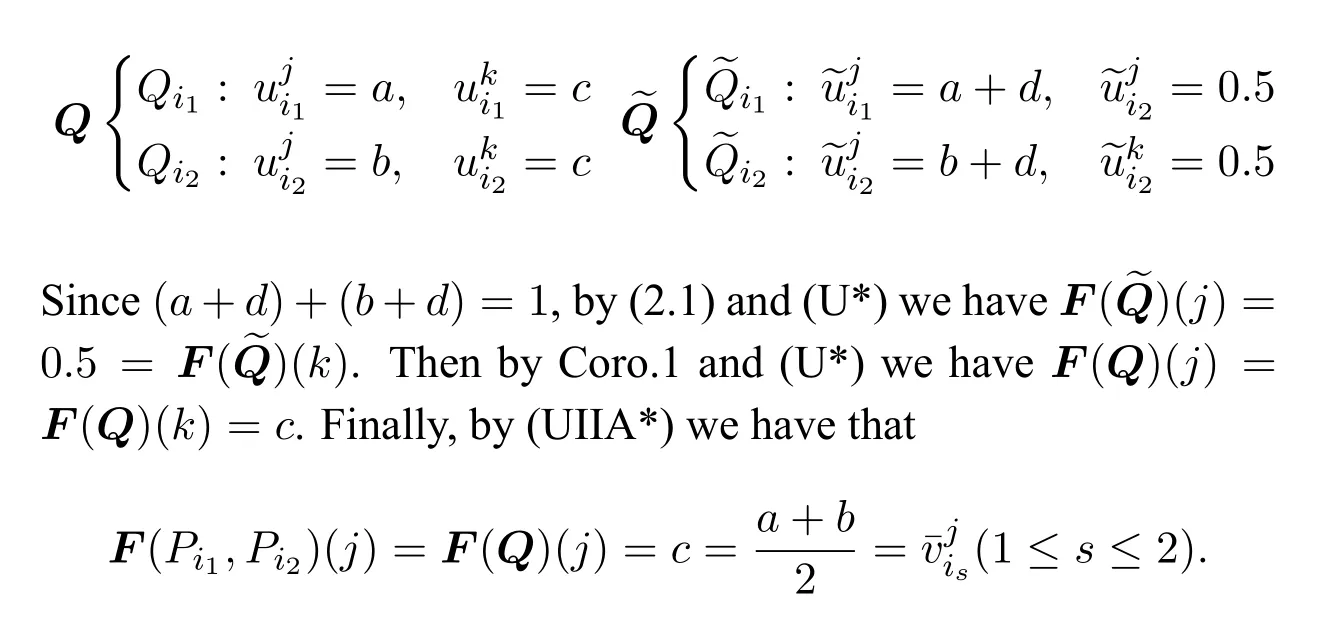

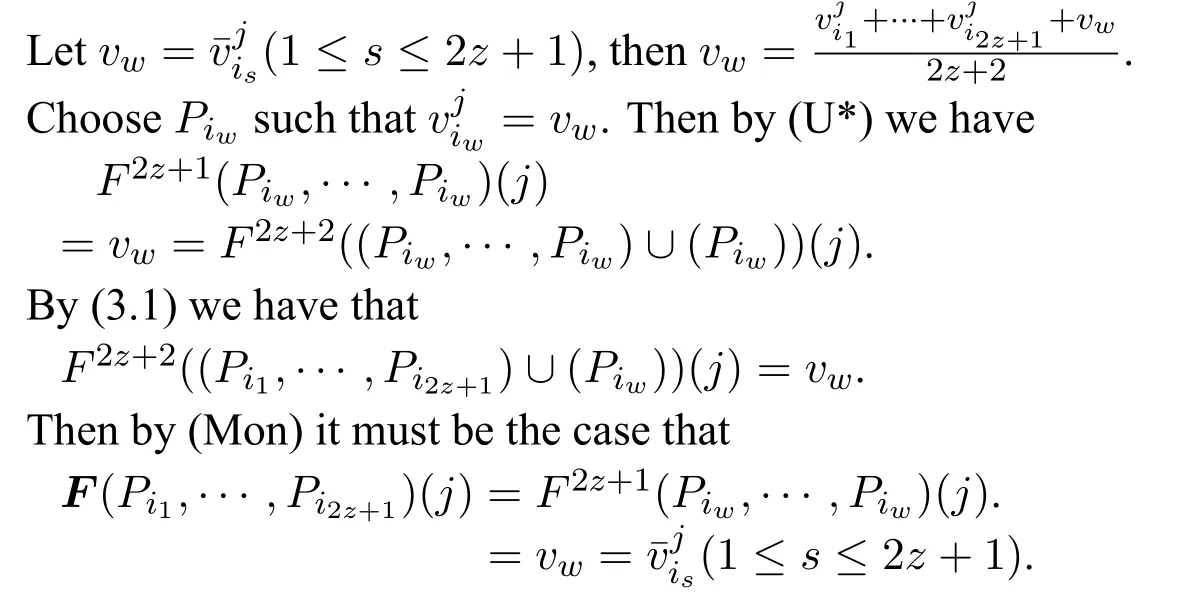
5 Improvement
5.1 Collective veto
5.2 Limit on the violation of majority
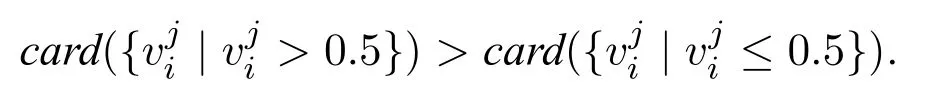
6 Conclusion