Sahlqvist Correspondence for Instantial Neighbourhood Logic*
Zhiguang Zhao
Abstract. In the present paper,we investigate the Sahlqvist-type correspondence theory for instantial neighbourhood logic (INL),which can talk about existential information about the neighbourhoods of a given world and is a mixture between relational semantics and neighbourhood semantics.The increased expressivity and its ability to talk about certain relational patterns of the neighbourhood function makes it possible to ask what kind of properties can this language define on the frame level,whether the“Sahlqvist”fragment of instantial neighbourhood logic could be larger than the rather small KW-fragment.(H.Hansen,2003)We have two proofs of the correspondence results,the first proof is obtained by using standard translation and minimal valuation techniques directly,the second proof follows M.Gehrke et al.(2005)and H.Hansen(2003),where we use bimodal translation method to reduce the correspondence problem in instantial neighbourhood logic to normal bimodal logics in classical Kripke semantics.We give some remarks and future directions at the end of the paper.
1 Introduction
Recently,a variant of neighbourhood semantics for modal logics was given,under the name of instantial neighbourhood logic(INL),where existential information about the neighbourhoods of a given world can be added.([5,13,2,3,4,14,15])This semantics is a mixture between relational semantics and neighbourhood semantics,and its expressive power is strictly stronger than neighbourhood semantics.
In this semantics,the(n+1)-ary modality□(ψ1,...,ψn;φ)is true at a worldwif and only if there exists a neighbourhoodS ∈N(w)such thatφis true everywhere inS,and eachψiis true atwi ∈Sfor somewi.This language has a natural interpretation as a logic of computation in open systems:□(ψ1,...,ψn;φ)can be interpreted as“in the system,the agent has an action to enforce the conditionφwhile simultaneously allowing possible outcomes satisfying each of the conditionsψ1,...,ψn”;this language can describe not only what properties can be guaranteed by an agent’s action,but also exactly what possible outcomes may be achieved from this action(see[3]).
Instantial neighbourhood logic is first introduced in [4],where the authors defines the notion of bisimulation for instantial neighbourhood logic,gives a complete axiomatic system,and determines its precise SAT complexity;in [13],the canonical rules are defined for instantial neighbourhood logic;in [2],the game-theoretic aspects of instantial neighbourhood logic is studied;in[3],a propositional dynamic logic IPDL is obtained by combining instantial neighbourhood logic with propositional dynamic logic (PDL),its sound and complete axiomatic system is given as well as its finite model property and decidability;in [5],the duality theory for instantial neighbourhood logic is developed via coalgebraic method;in[14],a tableau system for instantial neighbourhood logic is given which can be used for mechanical proof and countermodel search;in[15],a cut-free sequent calculus and a constructive proof of its Lyndon interpolation theorem is given.However,the Sahlqvist-type correspondence theory is still unexplored,which is the theme of this paper;in addition,the increased expressivity makes it possible to ask what kind of properties can this language define on the frame level,whether the“Sahlqvist”fragment of instantial neighbourhood logic could be larger than the rather small KW-fragment in [10] in monotone modal logic.
In this paper,we define the Sahlqvist formulas in the instantial neighbourhood modal language,and give two different proofs of correspondence results.The first proof is given by standard translation and minimal valuation techniques as in[6,Section 3.6],while the second proof uses bimodal translation method in monotone modal logic and neighbourhood semantics([10,11,12,1])to show that every Sahlqvist formula in the instantial neighbourhood modal language can be translated into a bimodal Sahlqvist formula in Kripke semantics,and hence has a first-order correspondent.The first proof is standard and it reveals how the instantial neighbourhood semantics have the relational pattern,and the second proof is simpler and easier to understand.
The structure of the paper is as follows:in Section 2,we give a brief sketch on the preliminaries of instantial neighbourhood logic,including its syntax and neighbourhood semantics.In Section 3,we define the standard translation of instantial neighbourhood logic into a two-sorted first-order language.In Section 4,we define Sahlqvist formulas in instantial neighbourhood logic,and prove the Sahlqvist correspondence theorem via standard translation and minimal valuation.In Section 5,we discuss the translation of instantial neighbourhood logic into normal bimodal logic,and prove Sahlqvist correspondence theorem via this bimodal translation.In Section 6,we give some examples.We give some remarks and further directions in Section 7.
2 Preliminaries on Instantial Neighbourhood Logic
In this section,we collect some preliminaries on instantial neighbourhood logic,which can be found in[4].
Syntax.The formulas of instantial neighbourhood logic are defined as follows:
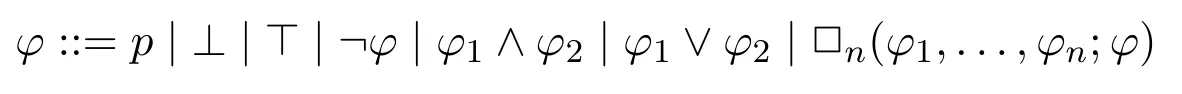
wherep ∈Prop is a propositional variable,□nis an (n+1)-ary modality for eachn ∈N.→,?can be defined in the standard way.An occurence ofpis said to bepositive(resp.negative)inφifpis under the scope of an even(resp.odd)number of negations.A formulaφis positive(resp.negative)if all occurences of propositional variables inφare positive(resp.negative).
Semantics.For the semantics of instantial neighbourhood logic,we use neighbourhood frames to interpret the instantial neighbourhood modality,one and the same neighbourhood function for all the(n+1)-ary modalities for alln ∈N.
Definition 1(Neighbourhood frames and models) Aneighbourhood frameis a pair F(W,N) where?is the set of worlds,N:W →P(P(W)) is a map called aneighbourhood function(notice that there is no restriction on what additional propertiesNshould satisfy,e.g.w ∈Xfor allX ∈N(w),or upward-closedness:X ∈N(w) andX ?YimpliesY ∈N(w)),whereP(W) is the powerset ofW.AvaluationonWis a mapV:Prop→P(W).A triple M(W,N,V)is called aneighbourhood modelor a neighbourhood model based on(W,N)if(W,N)is a neighbourhood frame andVis a valuation on it.
The semantic clauses for the Boolean part is standard.For the instantial neighbourhood modality□,the satisfaction relation is defined as follows:
M,w?□n(φ1,...,φn;φ)iff there isS ∈N(w)such that for alls ∈Swe have

Semantic properties of instantial neighbourhood modalities.It is easy to see the following lemma,which states that the(n+1)-ary instantial neighbourhood modality□nis monotone in every coordinate,and is completely additive(and hence monotone)in the firstncoordinates(even if the neighbourhood function is not upward-closed).This observation is useful in the algebraic correspondence analysis in instantial neighbourhood logic.
Lemma 1
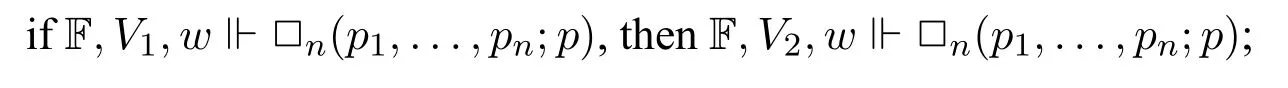
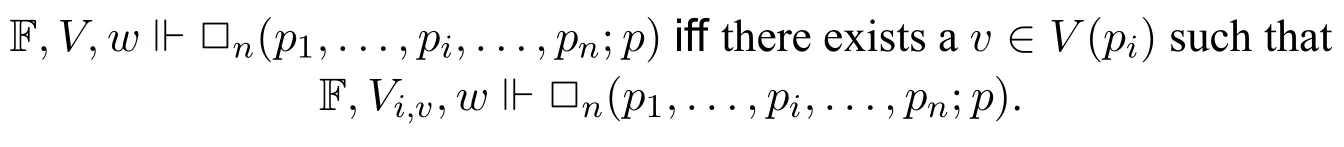
Algebraically,if we view the (n+1)-ary modality□nas an (n+1)-ary function:An+1→A,then(a1,...,an;a) is completely additive (i.e.preserve arbitrary joins) in the firstncoordinate,and monotone in the last coordinate.This observation is useful in the algebraic correspondence analysis(see Section 7).
Getting standard neighbourhood semantics and Kripke semantics from INL.
As we have already seen in[4],instantial neighbourhood logic can express standard monotone neighbourhood modalities by just takingn0,i.e.,
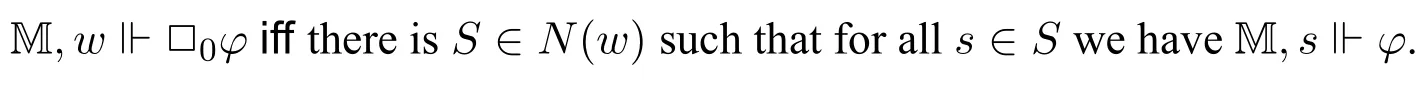
Indeed,from the definition ofNwe can define some induced(n+1)-ary relations,and instantial neighbourhood logic can reason about these relational structures.Here we take binary relation and the binary modality□1as an example:
We can define the following binary relationR1,?based on the neighbourhood functionN:
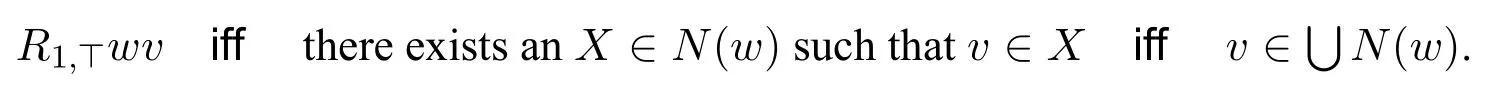
Then it is easy to see that
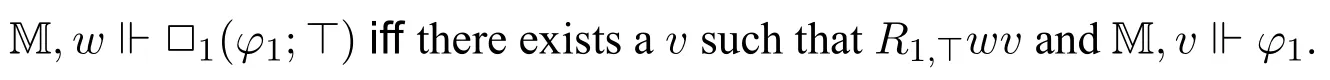
Therefore,instantial neighbourhood logic can talk about certain relational structures behind the neighbourhood function.Indeed,we will expand on this phenomenon later on(see Section 4.2)when we analyze when instantial neighbourhood logic become“normal”.
3 Standard Translation of Instantial Neighbourhood Logic
3.1 Two-sorted first-order language L1 and standard translation
Given the INL language,we consider the corresponding two sorted first-order languageL1,which is going to be interpreted in a two-sorted domainWw×Ws.For a more detailed treatment,see[10,7].This language is used in the treatment of the standard translation for neighbourhood semantics.The major pattern of this language is that we treat worlds and subsets of worlds as two different sorts,which makes it different from standard first-order language.In addition,allowing quantification over subsets of worlds makes the language have some flavor of second-order logic,but here we treat those subsets of worlds as first-order objects in the second domainWs.
This language has the following ingredients:
1.world variablesx,y,z,...,to be interpreted as possible worlds in the world domainWw;
2.subset variablesX,Y,Z,...,to be interpreted as objects in the subset domainWs{X |X ?Ww};1Notice that here the subset variables are treated as first-order variables in the subset domain Ws,rather than second-order variables in the world domain Ww.Indeed,when talking about standard translation in neighbourhood semantics,it is not possible to avoid talking about subsets of the domain,since the elements in N(w)are subsets of W.Therefore,we follow the tradition in monotone modal logic[10,p.34]to call this two-sorted language first-order.
3.a binary relation symbolR?,to be interpreted as the reverse membership relationR??Ws×Wwsuch thatR?Xxiffx ∈X;
4.a binary relation symbolRN,to be interpreted as the neighbourhood relationRN ?Ww×Wssuch thatRNxXiffX ∈N(x);
5.unary predicate symbolsP1,P2,…,to be interpreted as subsets of the world domainWw.
We also consider the following second-order languageL2which is obtained by adding second-order quantifiers?P1,?P2,…over the world domainWw.Existential second-order quantifiers?P1,?P2,...are interpreted in the standard way.Notice that here the second-order variablesP1,…are different from the subset variablesX,Y,Z,...,since the former are interpreted as subsets ofWw,and the latter are interpreted as objects inWs.
Now we define the standard translationSTw(φ)as follows:
Definition 2(Standard translation) For any INL formulaφand any world symbolx,the standard translationSTx(φ)ofφatxis defined as follows:
?STx(p):Px;
?STx(⊥):xx;
?STx(?):xx;
?STx(?φ):?STx(φ);
?STx(φ ∧ψ):STx(φ)∧STx(ψ);
?STx(φ ∨ψ):STx(φ)∨STx(ψ);
?STx(□n(φ1,...,φn;φ))?X(RNxX ∧?y(R?Xy →STy(φ))∧
?y1(R?Xy1∧STy1(φ1))∧...∧?yn(R?Xyn ∧STyn(φn))).
For any neighbourhood frame F(W,N),it is natural to define the following corresponding two-sorted Kripke frame F2(W,P(W),R?,RN),where
1.R??P(W)×Wsuch that for anyx ∈WandX ∈P(W),R?Xxiffx ∈X;
2.RN ?W × P(W) such that for anyx ∈WandX ∈P(W),RNxXiffX ∈N(x).
Given a two-sorted Kripke frame F2(W,P(W),R?,RN),a valuationVis defined as a mapV:Prop→P(W).Notice that here theP(W)in the definition ofVis understood as the powerset of the first domain,rather than the second domain itself.
For this standard translation,it is easy to see the following correctness result:
Theorem 3.For any neighbourhood frameF(W,N),any valuation V onF,any w ∈W,any INL formula φ,
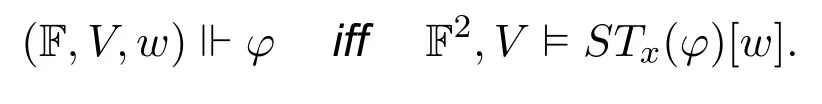
4 Sahlqvist Correspondence Theorem in Instantial Neighbourhood Logic via Standard Translation
In this section,we will define the Sahlqvist formulas in instantial neighbourhood logic and prove the correspondence theorem via standard translation and minimal valuation method.First we recall the definition of Sahlqvist formulas in normal modal logic.Then we identify the special situations where the instantial neighourhood modalities“behave well”,i.e.have good quantifier patterns in the standard translation.Finally,we define INL-Sahlqvist formulas step by step in the style of[6,Section 3.6],and prove the correspondence theorem.The reason why we still have a proof by standard translation and minimal valuation method is that it helps to recognize the“relational”pattern in this neighbourhood-type semantics.
4.1 Sahlqvist formulas in normal modal logic
In this subsection we recall the syntactic definition of Sahlqvist formulas in normal modal logic(see[6,Section 3.6,Definition 3.51]).
Definition 4(Sahlqvist formulas in normal modal logic) Aboxed atomis a formula of thep,whereare (not necessarily distinct) boxes.In the case wheren0,the boxed atom is justp.
ASahlqvist antecedent φis a formula built up from⊥,?,boxed atoms,and negative formulas,using∧,∨and existential modal operators◇(unary diamond)and Δ(polyadic diamond).ASahlqvist implicationis an implicationφ →ψin whichψis positive andφis a Sahlqvist antecedent.
A Sahlqvist formula is a formula that is built up from Sahlqvist implications by applying boxes and conjunctions,and by applying disjunctions only between formulas that do not share any proposition variables.
As we can see from the definition above,the Sahlqvist antecedents are built up by⊥,?,p,pand negative formulas using∧,∨,◇,Δ.If we consider the standard translations of Sahlqvist antecedents,the inner part is translated into universal quantifiers,and the outer part are translated into existential quantifiers.
4.2 Special cases where the instantial neighbourhood modalities become“normal”
As is mentioned in[4,Section 7]and as we can see in the definition of the standard translation,the quantifier pattern of□n(φ1,...,φn;φ)is similar to the case of monotone modal logic([10])which has an??pattern.As a result,even with two layers of INL modalities the complexity goes beyond the Sahlqvist fragment.However,we can still consider some special situations where we can reduce the modality to ann-ary normal diamond or a unary normal box.
n-ary normal diamond.We first consider the case□n(φ1,...,φn;φ)whereφis apure formulawithout any propositional variables,i.e.,all propositional variables are substituted by⊥or?.In this caseSTx(φ)is a first-order formulaαφ(x)without any unary predicate symbolsP1,P2···.Therefore,in the shape of the standard translation of□n(φ1,...,φn;φ),the universal quantifier?yis not touched during the computation of minimal valuation,since there is no unary predicate symbol there.Indeed,we can consider the following equivalent form ofSTx(□n(φ1,...,φn;φ)):
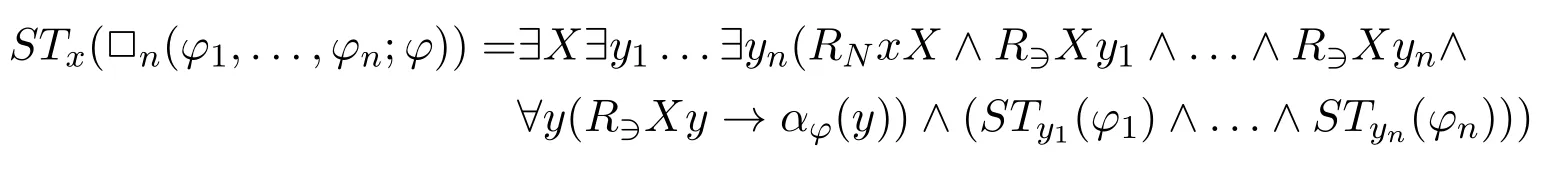
NowSTx(□n(φ1,...,φn;φ)) is essentially in a form similar toSTx(◇ψ) in the normal modal logic case;indeed,when we compute the minimal valuation here,RNxX ∧R?Xy1∧...∧R?Xyn ∧?y(R?Xy →αφ(y))can be recognized as an entirety and stay untouched during the process.Indeed,here we can use the formula?X(RNxX ∧R?Xy1∧...∧R?Xyn ∧?y(R?Xy →αφ(y)))to define an(n+1)-ary relation symbolRn,φxy1...yn,and we denote the semantic counterpart of this relation also byRn,φ,then it is easy to see that
M,w?□n(φ1,...,φn;φ)iff there existv1,...,vnsuch thatRn,φwv1...vnand
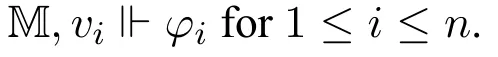
This is exactly how then-ary Δ modality is defined in standard modal logic settings.From now onwards we can denote□n(φ1,...,φn;φ)by Δn,φ(φ1,...,φn)whereφis pure.
Unary Normal Box.As we can see from above,in□n(φ1,...,φn;φ),we can replace propositional variables inφby⊥and?to obtainn-ary normal diamond modalities.By using the composition with negations,we can get the unary normal box modality,i.e.we can have a modality
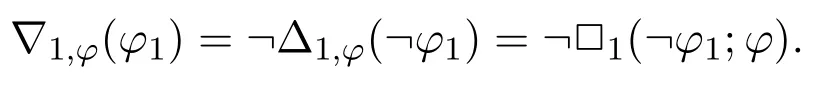
Now we can consider the standard translation of?1,φ(φ1):
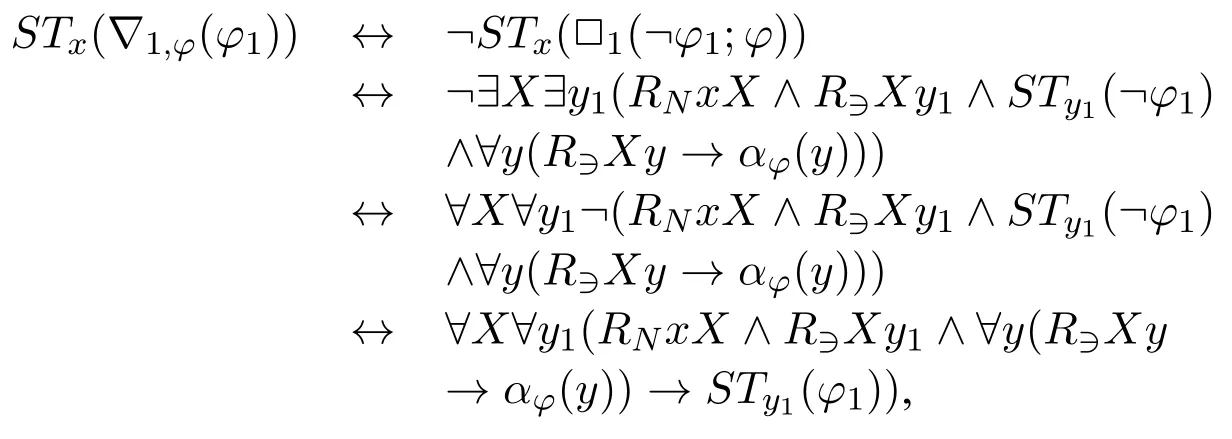
where?y(R?Xy →αφ(y)) does not contain unary predicate symbolsP1,P2,···.Now we can see thatSTx(?1,φ(φ1)) has a form similar toSTx(□ψ) where□is a normal unary box,by takingRNxX ∧R?Xy1∧?y(R?Xy →αφ(y))as an entirety.
4.3 The definition of INL-Sahlqvist formulas in instantial neighbourhood logic
Now we can define the INL-Sahlqvist formulas in instantial neighbourhood logic step by step in the style of[6,Section 3.6].The basic proof structure is similar to the basic modal logic setting,namely we first rewrite the standard translation of the modal formula into a specific shape,and then read off the minimal valuation directly from the shape,while here the manipulation of quantifiers is more complicated and needs to take more care.
4.3.1 Very simple INL-Sahlqvist implications
Definition 5(Very simple INL-Sahlqvist implications) Avery simple INL-Sahlqvist antecedent φis defined as follows:
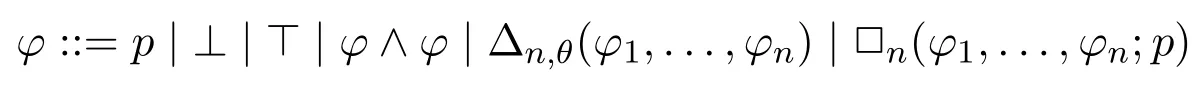
wherep ∈Prop is a propositional variable,θis a pure formula without propositional variables.Avery simple INL-Sahlqvist implicationis an implicationφ →ψwhereψis positive,andφis a very simple INL-Sahlqvist antecedent.
For very simple INL-Sahlqvist implications,we allown-ary normal diamonds Δn,θin the construction ofφ,while for the(n+1)-ary modality□n,we only allow propositional variables to occur in the(n+1)-th coordinate.
We can show that very simple INL-Sahlqvist implications have first-order correspondents:
Theorem 6.For any given very simple INL-Sahlqvist implication φ →ψ,there is a two-sorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,
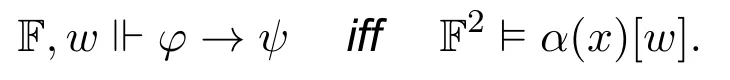
ProofThe proof strategy is similar to[6,Theorem 3.42,Theorem 3.49],with some differences in treating□n(φ1,...,φn;p).
We first start with the two-sorted second-order translation ofφ →ψ,namely?P1...?Pn?x(STx(φ)→STx(ψ)),whereSTx(φ),STx(ψ) are the two-sorted first-order standard translations ofφ,ψ.
For any very simple INL-Sahlqvist antecedentφ,we consider the shape ofβSTx(φ)defined inductively,
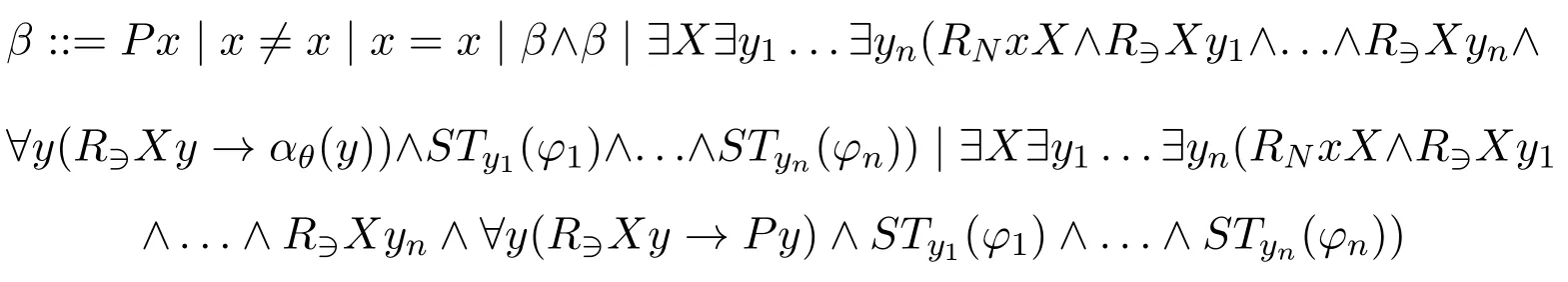
Now we can denoteRNxX ∧R?Xy1∧...∧R?XynasRnXxy1...ynandR?1,θXfor?y(R?Xy →αθ(y)),and thus get
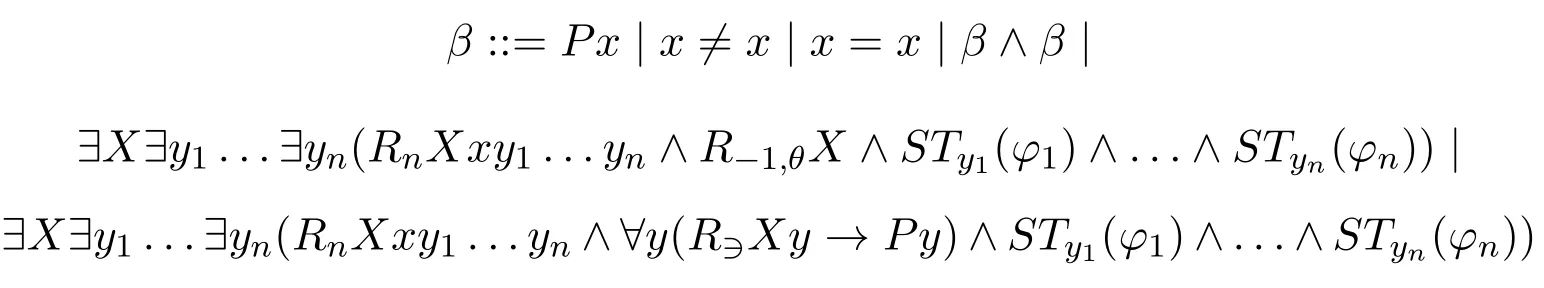
By using the equivalences
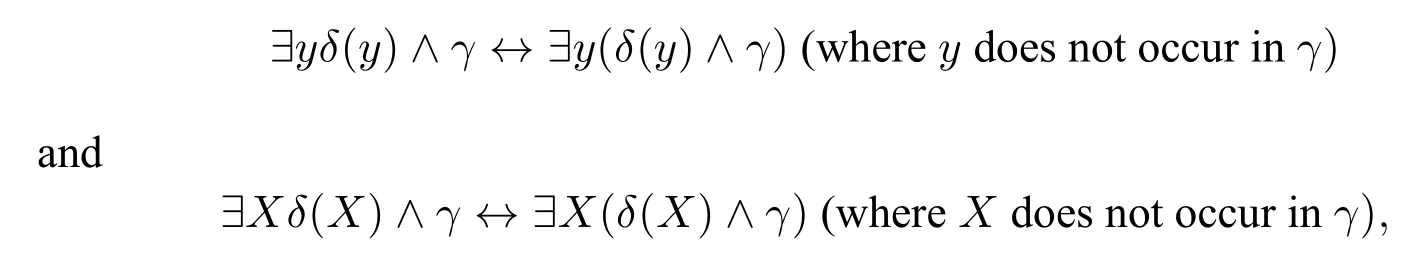
Itiseasy tosee thatthetwo-sorted first-orderformulaβSTx(φ)is equivalent to a f ormula ofthe form∧ATProp),where:
? ATProp is a conjunction of formulas of the form?y(R?Xy →Py)orPworwworww.
Therefore,by using the equivalences
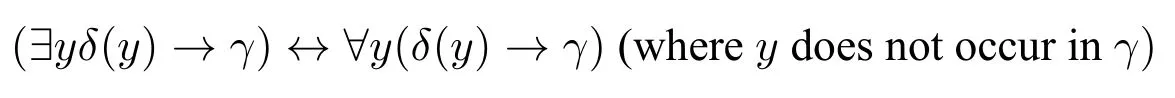
and
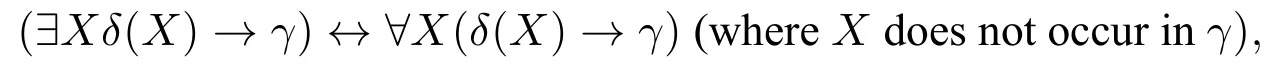
it is immediate that?P1...?Pn?x(STx(φ)→STx(ψ))is equivalent to
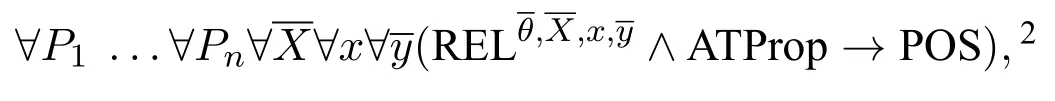
2Notice that the quantifiers ?P1...?Pnare second-order quantifiers over the world domain,andare first-order quantifiers over the subset domain.
Now we can use similar strategy as in[6,Theorem 3.42,Theorem 3.49].To make it easier for later parts in the paper,we still mention how the minimal valuation and the resulting first-order correspondent formula look like.Without loss of generality we suppose that for any unary predicatePthat occurs in the POS also occurs in AT;otherwise we can substitutePbyλu.uuforPto eliminateP(see[6,Theorem 3.42]).
Now consider a unary predicate symbolPoccuring in ATProp,andPx1,...,Pxn,?y(R?X1y →Py),…,?y(R?Xmy →Py)are all occurences ofPin ATProp.By takingσ(P)to be
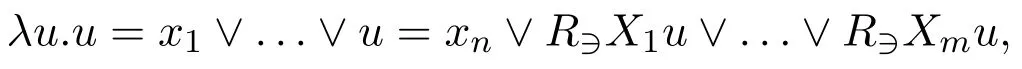
we get the minimal valuation.The resulting first-order correspondent formula is
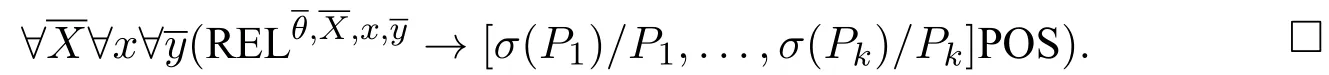
From the proof above,we can see that the part corresponding to Δn,θ(φ1,...,φn)is essentially treated in the same way as ann-ary diamond in the normal modal logic setting,and□n(φ1,...,φn;p)is treated as Δ(◇φ1∧...∧◇φn ∧□p)where Δ is an(n+1)-ary normal diamond,◇is a unary normal diamond and□is a unary normal box,therefore we can guarantee the compositional structure of quantifiers in the antecedent to be??as a whole.
4.3.2 Simple INL-Sahlqvist implications
Similar to simple Sahlqvist implications in basic modal logic,here we can define simple INL-Sahlqvist implications:
Definition 7(Simple INL-Sahlqvist implications) Apseudo-boxed atom ζis defined as follows:
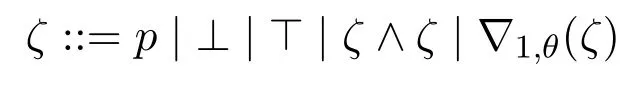
whereθis a pure formula without propositional variables.Based on this,asimple INL-Sahlqvist antecedent φis defined as follows:
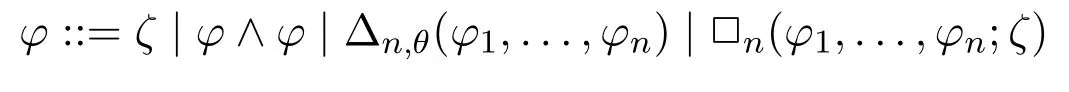
whereθis a pure formula without propositional variables andζis a pseudo-boxed atom.Asimple INL-Sahlqvist implicationis an implicationφ →ψwhereψis positive,andφis a simple INL-Sahlqvist antecedent.
Theorem 8.For any given simple INL-Sahlqvist implication φ →ψ,there is a twosorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,

ProofWe use similar proof strategy as [6,Theorem 3.49].The part that we need to take care of is the way to compute the minimal valuation.Now without loss of generality (by renaming quantified variables) we have the following shape ofβSTx(ζ)defined inductively for any pseudo-boxed atomζ:
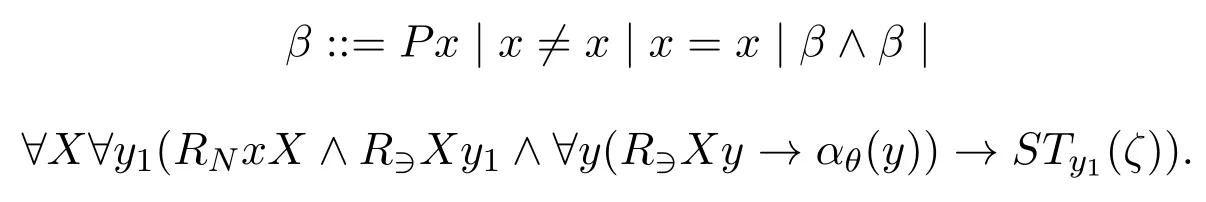
The shape ofβSTx(φ) is defined inductively for any simple Sahlqvist antecedentφ:
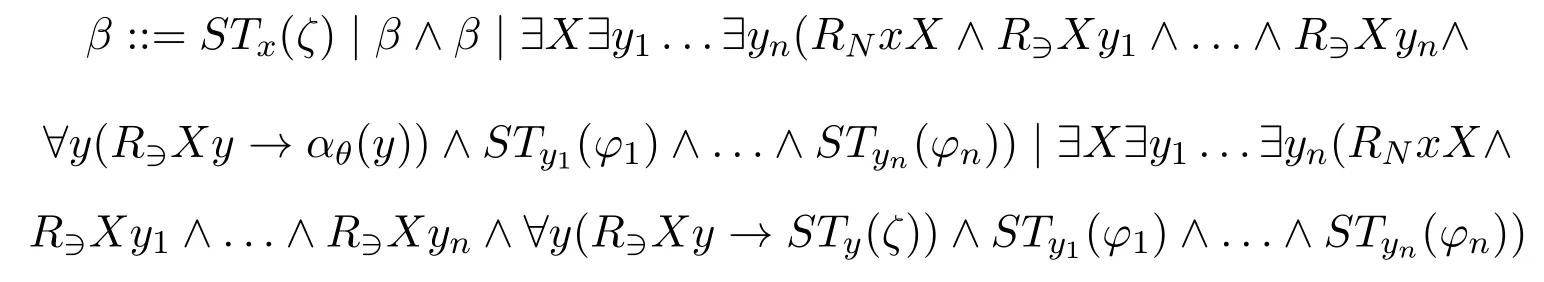
Now we use the abbreviationRnXxy1...ynforRNxX∧R?Xy1∧...∧R?XynandR?1,θXfor?y(R?Xy →αθ(y)) (note that the only possible free variable inαθ(y) isy),then by the equivalence (?Xα →β)??X(α →β),the shape ofβSTx(ζ)can be given as follows:
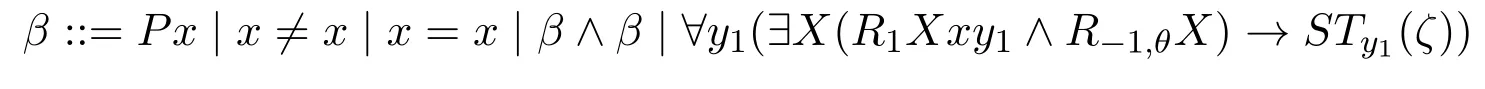
The shape ofβSTx(φ)can be given as follows:
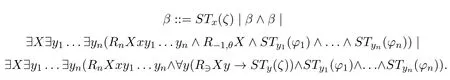
Now we denote?X(R1Xxy1∧R?1,θX)asR?2,θxy1,and we get the shape of pseudo-boxed atomβSTx(ζ)as follows:
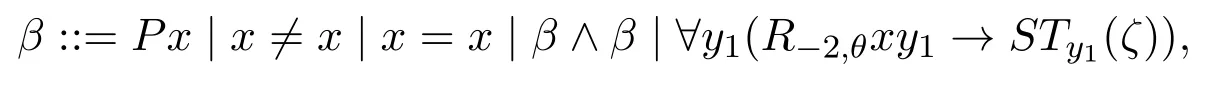
Now using the following equivalences:
? (φ →?z(ψ(z)→γ))??z(φ ∧ψ(z)→γ)(wherezdoes not occur inφ);
? (φ →(ψ →γ))?(φ ∧ψ →γ);
? (φ →(ψ ∧γ))?((φ →ψ)∧(φ →γ));
??z(ψ(z)∧γ(z))?(?zψ(z)∧?zγ(z));


4.3.3 INL-Sahlqvist implications
In the present section,we add negated formulas and disjunctions in the antecedent part,which is analogous to the first half of[6,Definition 3.51].
Definition 9(INL-Sahlqvist implications) AnINL-Sahlqvist antecedent φis defined as follows:
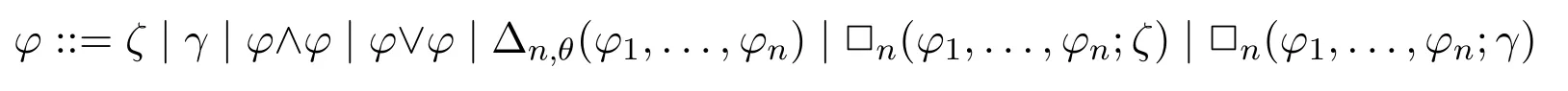
whereθis a pure formula without propositional variables,ζis a pseudo-boxed atom andγis a negative formula.AnINL-Sahlqvist implicationis an implicationφ →ψwhereψis positive,andφis an INL-Sahlqvist antecedent.
Theorem 10.For any given INL-Sahlqvist implication φ →ψ,there is a two-sorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,

ProofWe use similar proof strategy as[6,Theorem 3.54].The part that we need to take care of is the way to compute the minimal valuation.Now for each INL-Sahlqvist antecedentφ,we consider the shape ofβSTx(φ):
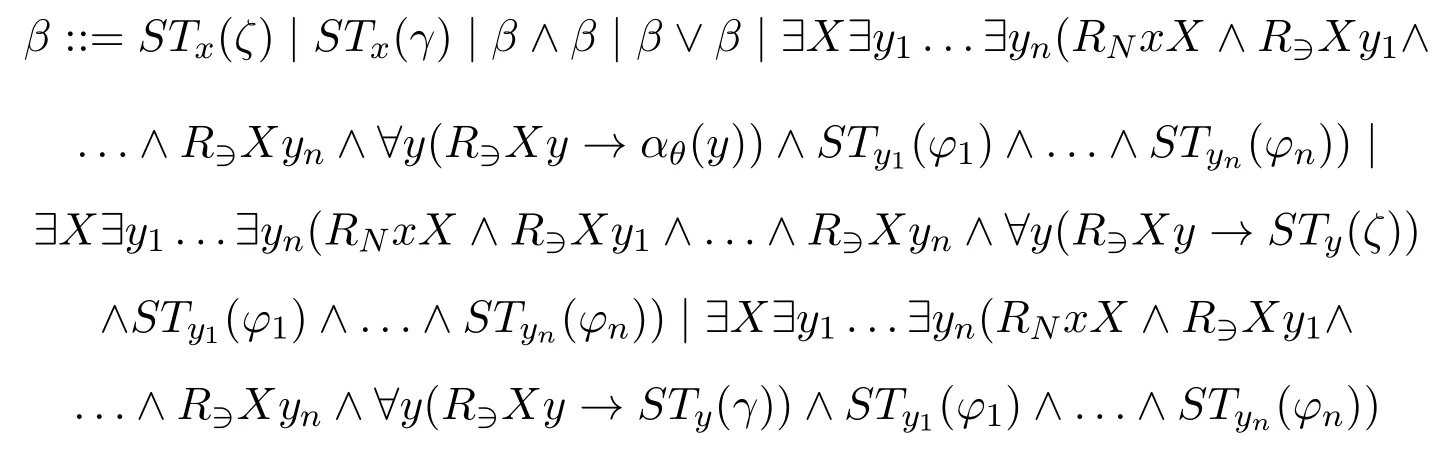
whereθis a pure formula without propositional variables,ζis a pseudo-boxed atom andγis a negative formula.
We use the abbreviationRnXxy1,...ynforRNxX ∧R?Xy1∧...∧R?XynandR?1,θXfor?y(R?Xy →αθ(y)),we can rewrite the shape ofβSTx(φ)as follows:
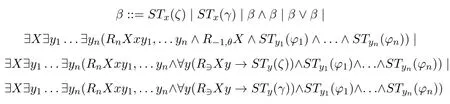
whereθis a pure formula without propositional variables,ζis a pseudo-boxed atom andγis a negative formula.
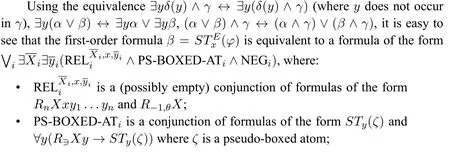
? NEGiis a conjunction of formulas of the formSTy(γ)and?y(R?Xy →STy(γ))whereγis a negative formula.
Now let us consider the standard translation of INL-Sahlqvist implicationφ →ψwhereφis an INL-Sahlqvist antecedent andψis a positive formula.ForβSTEx(φ →ψ),we have the following equivalence:

Now it is easy to see that?NEGi ∨STx(ψ) is equivalent to a first-order formula which is positive in all unary predicates.We can now use essentially the same proof strategy as Theorem 8. □
As we can see from the proofs above,the key point is the quantifier pattern of the two-sorted standard translation of the modalities,i.e.the outer part of the structure of an INL-Sahlqvist antecedent are translated into existential quantifiers,and the inner part is translated into universal quantifiers.
4.3.4 INL-Sahlqvist formulas
In the present section,we build Sahlqvist formulas from Sahlqvist implications by applying?1,θ(·)(whereθis pure),∧and∨,which is analogous to the second half of[6,Definition 3.51].
Definition 11(INL-Sahlqvist formulas) AnINL-Sahlqvist formula φis defined as follows:
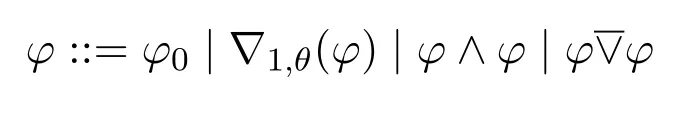
whereφ0is an INL-Sahlqvist implication,θis a pure formula without propositional variables,is a disjunction such that the twoφs share no propositional variable.
Theorem 12.For any given INL-Sahlqvist formula φ,there is a two-sorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,

ProofSimilar to[6,Lemma 3.53]. □
5 Bimodal Translation of Instantial Neighbourhood Logic
In the present section we give the second proof of Sahlqvist correspondence theorem,by using a bimodal translation into a normal bimodal language.The methodology is similar to[10,7],but with slight differences.
5.1 Normal bimodal language and two-sorted Kripke frame
In this subsection,we introduce the normal bimodal language and two-sorted Kripke frame.For a more detailed treatment,see[10,7].
As we can see in Section 3,for any given neighbourhood frame F(W,N),there is an associated two-sorted Kripke frame F2(W,P(W),R?,RN),where
1.R??P(W)×Wsuch that for anyx ∈WandX ∈P(W),R?Xxiffx ∈X;
2.RN ?W × P(W) such that for anyx ∈WandX ∈P(W),RNxXiffX ∈N(x).
In this kind of semantic structures,we can define the following two-sorted normal bimodal language:
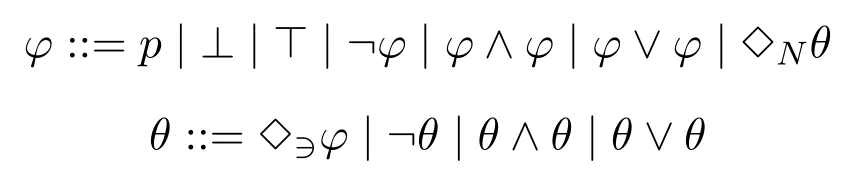
whereφis a formula of theworld typeand will be interpreted in the first domain,andθis a formula of thesubset typeand will be interpreted in the second domain.We can also define□?and□Nin the standard way.
Given a two-sorted Kripke frame F2(W,P(W),R?,RN),a valuationVis defined as a mapV:Prop→P(W),where propositional variables are interpreted as subsets of the first domain.The satisfaction relation ?is defined as follows,for anyw ∈Wand anyXinP(W)(here we omit the Boolean connectives):
? F2,V,w?piffw ∈V(p);
? F2,V,w?◇Nθiff there is anX ∈P(W)such thatRNwXand F2,V,X?θ;
? F2,V,X?◇?φiff there is aw ∈Wsuch thatR?Xwand F2,V,w?φ.
5.2 Bimodal translation
Now we are ready to define the translationτfrom the INL language to the twosorted normal bimodal language:
Definition 13(Bimodal translation) Given any INL formulaφ,the bimodal translationτ(φ)is defined as follows:
?τ(p)p;
?τ(⊥)⊥;
?τ(?)?;
?τ(?φ)?τ(φ);
?τ(φ1∧φ2)τ(φ1)∧τ(φ2);
?τ(φ1∨φ2)τ(φ1)∨τ(φ2);
?τ(φ1→φ2)τ(φ1)→τ(φ2);
?τ(□n(φ1,...,φn;φ))◇N(◇?τ(φ1)∧...∧◇?τ(φn)∧□?τ(φ)).
It is easy to see the following correctness result:
Theorem 14.For any neighbourhood frameF(W,N),any valuation V onF,any w ∈W,any INL formula φ,
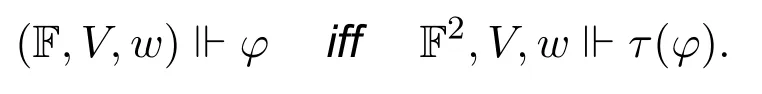
5.3 Sahlqvist correspondence theorem via bimodal translation
To discuss the Sahlqvist correspondence theorem via bimodal translation,we first discuss how the Sahlqvist fragment in normal bimodal logic looks like.
First of all,we have the following observation that for?1,θ(ζ)whereθis pure,its bimodal translation is□N(□?τ(ζ)∨?□?τ(θ)),i.e.□N(□?τ(θ)→□?τ(ζ)).This formula is not a box itself applied toτ(ζ),but its standard translation into first-order logic is
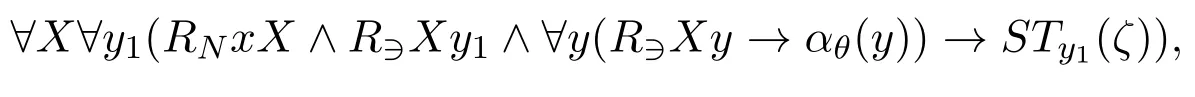
which means that we can treatRNxX ∧R?Xy1∧?y(R?Xy →αθ(y))as an entirety and therefore we can treat□N(□?τ(θ)→□?τ(ζ))like a boxed formula.From here onwards we will also call formulas of the shape□N(□?τ(θ)→□?τ(ζ)) boxed atoms ifτ(ζ)is a boxed atom.
Now,similar to the normal modal logic case,we can define the bimodal Sahlqvist antecedents in the normal bimodal logic built up by boxed atoms and negative formulas in the inner part generated by∧,∨,◇?,◇N,where the formulas are of the right type,and therefore bimodal Sahlqvist implications are defined in the standard way.A bimodal Sahlqvist formula is built up from bimodal Sahlqvist implications by applying boxes,□N(□?τ(θ)→□?(·)),∧and∨whereθis pure and∨is only applied to formulas which share no propositional variable.
Theorem 15.For any bimodal Sahlqvist formula φ,there is a two-sorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,
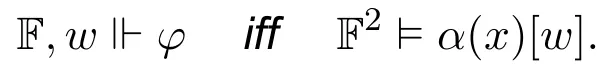
ProofBy adaptation of the proofs of Theorem 3.42,3.49,3.54 and Lemma 3.53 in[6]to the bimodal setting. □
Now we can prove Sahlqvist correspondence theorem by using bimodal translation:
Theorem 16.For any INL-Sahlqvist implication φ →ψ,τ(φ →ψ)is a Sahlqvist implication in the normal bimodal language.
ProofAs we know,the shape of an INL-Sahlqvist antecedent is given as follows:
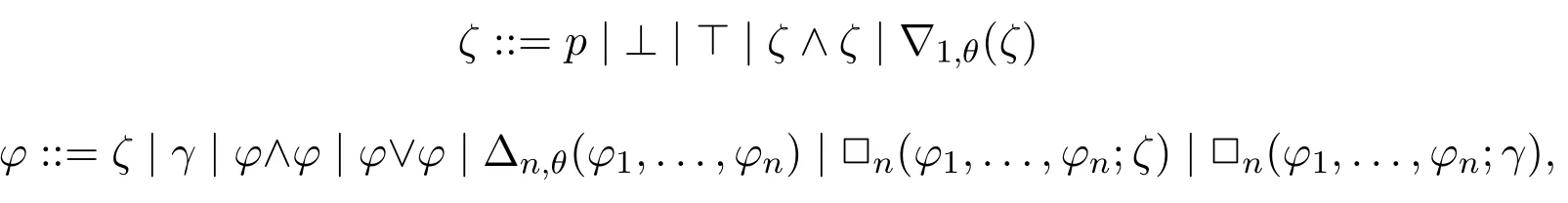
whereθis a pure INL formula without propositional variables,ζis a pseudo-boxed atom,andγis a negative formula.Therefore,the bimodal translations ofτ(ζ) andτ(φ)have the following shape:
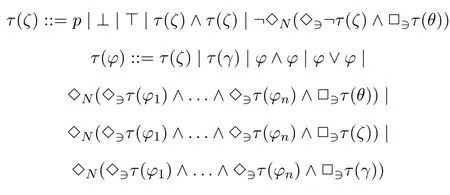
Now we analyze the shape above.For the bimodal translation of a pseudo-boxed atomζin the INL language,?◇N(◇??τ(ζ)∧□?τ(θ))is equivalent to□N(□?τ(ζ)∨?□?τ(θ)).sinceθis a pure formula without propositional variables,τ(ζ) can be treated as a conjunction of boxed atoms in the bimodal language.
Now we examineτ(φ).It is built up byτ(ζ) (a conjunction of boxed atoms)andτ(γ) (a negative formula),generated by∧,∨and the three special shapes ofτ(□n(φ1,...,φn;φ))whereφare pure formulas without propositional variables(theθcase),pseudo-boxed atoms(theζcase)or negative formulas(theγcase).It is easy to see thatτ(φ) is built up by pure formulas3Indeed,pure formulas are both negative and positive formulas in every propositional variable p,since their values are constants and p does not occur in them.,boxed atoms and negative formulas in the bimodal language,generated by◇?,◇N,∧,∨,thus of the shape of Sahlqvist antecedent in the bimodal language.Therefore,τ(φ →ψ)is a Sahlqvist implication in the normal bimodal language. □
Theorem 17.For any INL-Sahlqvist formula φ,its bimodal translation τ(φ)is a bimodal Sahlqvist formula.
ProofWe prove by induction.For the basic case and the∧and∨case,it is easy.For the?1,θ(ζ)case whereθis pure andζis an INL-Sahlqvist formula,by induction hypothesis,τ(ζ)is a bimodal Sahlqvist formula.By our definition,□N(□?τ(θ)→□?τ(ζ))is also a bimodal Sahlqvist formula. □
Theorem 18.For any INL-Sahlqvist formula φ,there is a two-sorted first-order local correspondent α(x)such that for any neighbourhood frameF(W,N),any w ∈W,
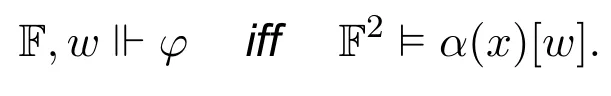
ProofBy Theorem 15 and Theorem 17. □
6 Examples
In this section,we give some examples of INL-Sahlqvist implications.Example 19Consider the formula□1(p;?)→?□1(?p;?),its standard translation is
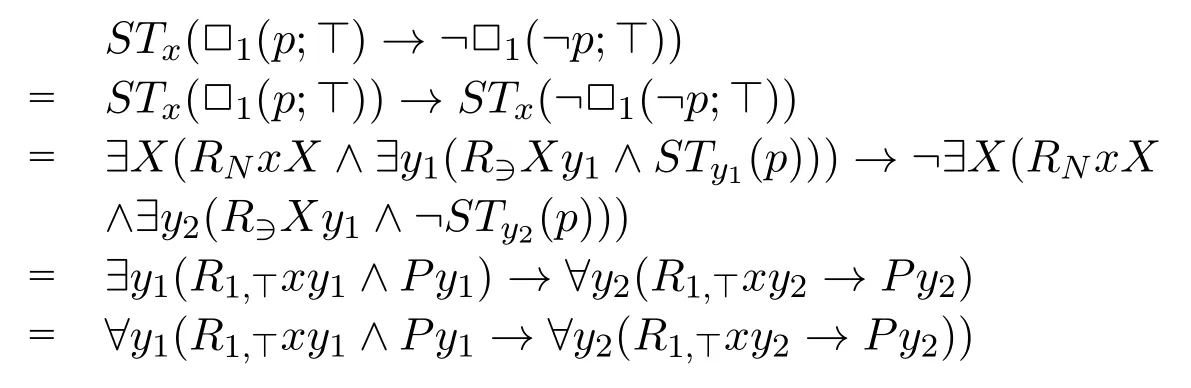
the minimal valuation forPisλz.zy1,therefore the local first-order correspondent of□1(p;?)→?□1(?p;?)is
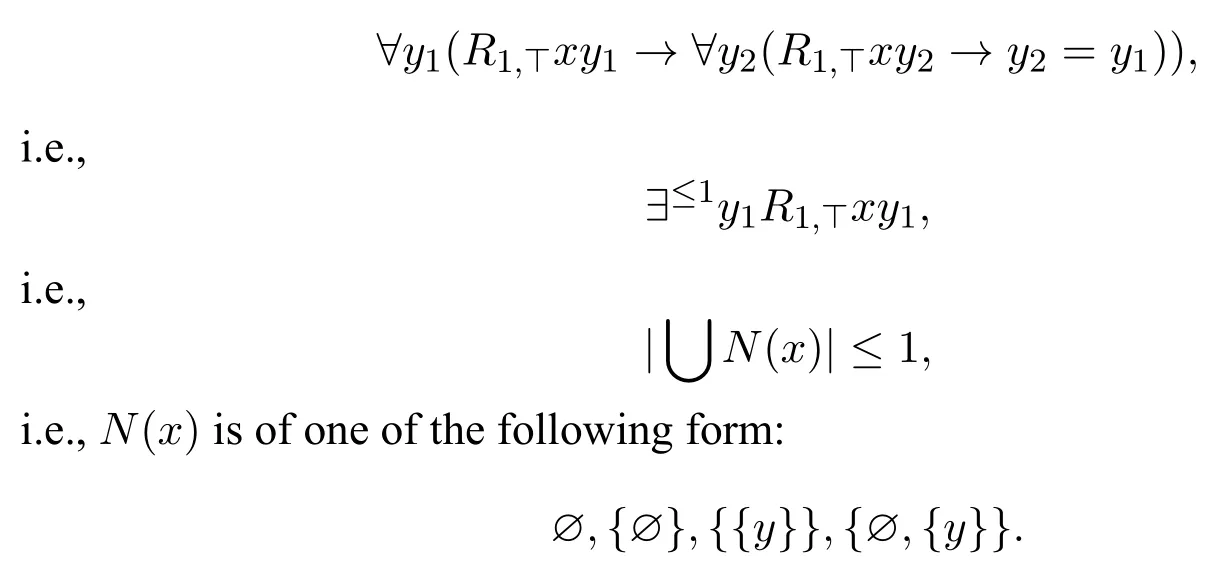
Example 20Consider the formula□1(□1(p;?);?)→□1(p;?),its standard translation is
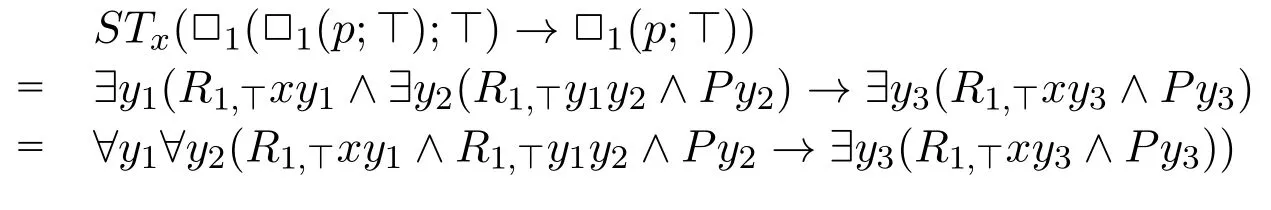
the minimal valuation isλz.zy2,therefore the local first-order correspondent of□1(□1(p;?);?)→□1(p;?)is
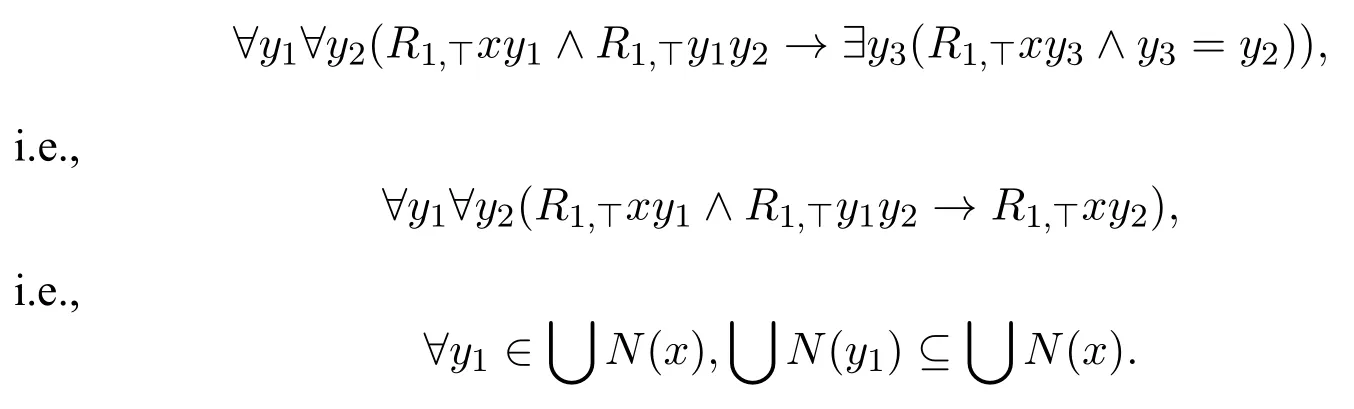
As we can see from the examples,instantial neighbourhood logic can talk about the“relational part”of the neighbourhood function,this is one of the reason to investigate the correspondence theory of instantial neighbourhood logic.
7 Discussions and Further Directions
In this paper,we give two different proofs of the Sahlqvist correspondence theorem for instantial neighbourhood logic,the first one by standard translation and minimal valuation,and the second one by reduction using the bimodal translation into a normal bimodal language.We give some remarks and further directions here.
Algebraic correspondence method using the algorithm ALBA.In[8],Sahlqvist and inductive formulas(an extension of Sahlqvist formulas,see[9]for further details)are defined based on duality-theoretic and order-algebraic insights.The Ackermann lemma based algorithm ALBA is given,which effectively computes first-order correspondents of input formulas/inequalities,and succeed on the Sahlqvist and inductive formulas/inequalities.In this approach,Sahlqvist and inductive formulas are defined in terms of the order-theoretic properties of the algebraic interpretations of the logical connectives.Indeed,in the dual complex algebra A of Kripke frame,the good properties of the connectives are the following:
? Unary◇is interpreted as a map◇A:A→A,which preserves arbitrary joins,i.e.◇A(∨a)∨◇Aaand◇A⊥⊥.Similarly,n-ary diamonds are interpreted as maps which preserve arbitrary joins in every coordinate.
? Unary□is interpreted as a map□A:A→A,which preserves arbitrary meets,i.e.□A(∧a)∧□Aaand□A??.Preserving arbitrary meets guarantees the map□A:A→A to have a left adjoint ?A:A→A such that ?Aa ≤biffa ≤□Ab.
As we have seen from Section 2,the algebraic interpretation of□n(φ1,...,φn;φ)preserves arbitrary joins in the firstncoordinates,and is monotone in the last coordinate.Therefore,we can adapt the ALBA method to the instantial neighbourhood logic case.In addition to this,we can also define INL-inductive formulas based on the algebraic properties of the instantial neighbourhood connectives,to extend INLSahlqvist formulas to INL-inductive formulas as well as to the language of instantial neighbourhood logic with fixpoint operators.
Completeness and canonicity.Other issues that we do not study in the present paper include completeness of logics axiomatized by INL-Sahlqvist formulas and canonicity.For the proof of completeness,we need to establish the validity of INLSahlqvist formulas on their corresponding canonical frames,where canonicity and persistence might play a role(see[6,Chapter 5]).

