Faculty of Economic Mathematics,University of Economics and Law,Ho Chi Minh City,Vietnam Vietnam National University,Ho Chi Minh City,Vietnam E-mail:phuongl@uel.edu.vn

Abstract Let 0<α,β0f oralls,t≥0.The main technique we use is the method of moving spheres in integral forms.Since our assumptionsare more general than those in the previous literature,some new ideas are introduced to overcome this difficulty.

Key words Higher fractional order system;integral system;general nonlinearity;method of moving spheres;classification of solutions

1 Introduction

Let

n

≥2 be an integer,

α,β

be real numbers satisfying 0

<α,β<n

,and

f,g

∈

C

([0

,

∞)×[0

,

∞))be two nonnegative functions.We study the semilinear elliptic system

and the related integral system

Throughout this paper,we study nonnegative solutions of(1.1)in classical sense.That is,we call(

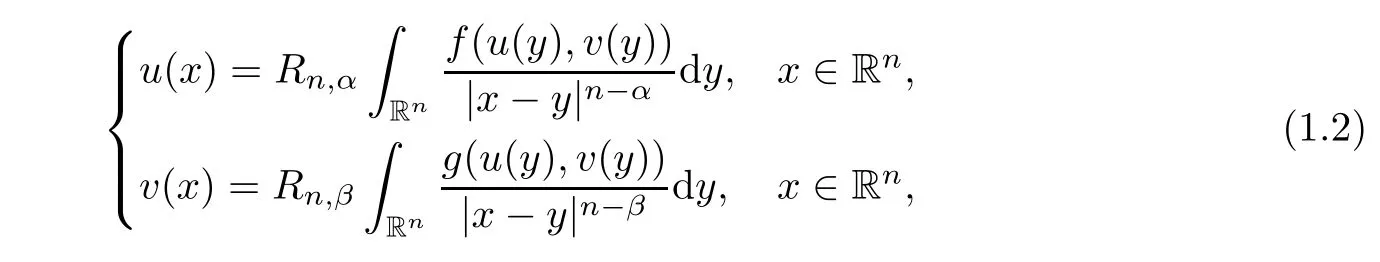
u,v

)a nonnegative solution of(1.1)if

u,v

≥0,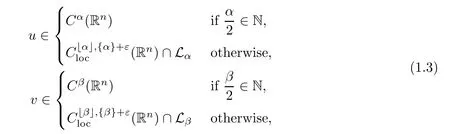

and(

u,v

)veri fies(1.1)point wise,where

ε>

0 is arbitrarily small.Moreover,(

u,v

)is called trivial if(

u,v

)≡(0

,

0).

In their pioneering article[2],Chen,Li and Ou introduced the method of moving planes in integral forms and used it to establish the radial symmetry of any nonnegative solution to the integral equation

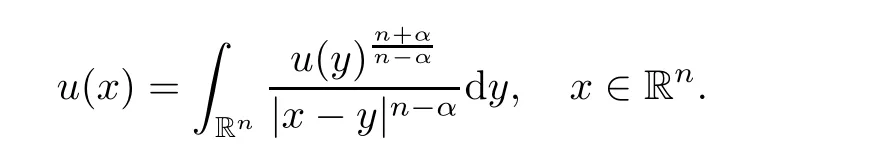
Hence they solved an open problem posed by Lieb[3]regarding the best constant in a Hardy-Little wood-Sobolev inequality.Later,Chen and Li[4]extended this result to the integral system

The first purpose of our paper is to classify nonnegative solutions of system(1.2)with more general nonlinearities

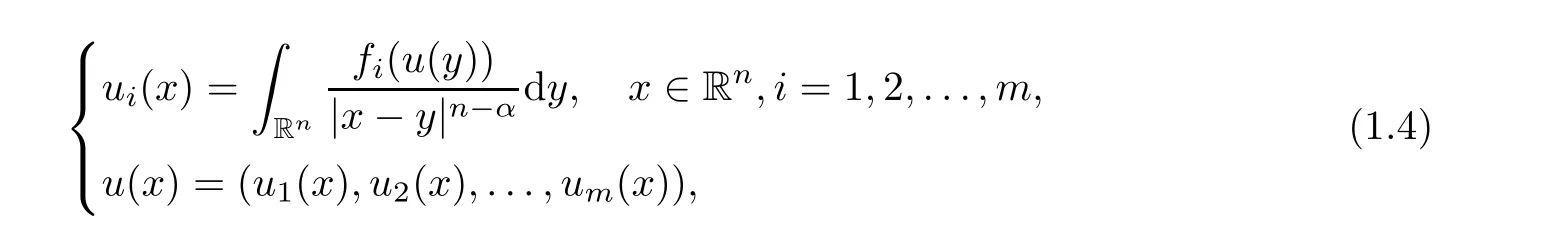
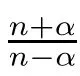
f

and

g

.Our monotonicity conditions on

f

and

g

are similar to those in[9].However,we do not assume

f,g

∈

C

or

α

=

β

.To overcome the difficulty caused by weaker assumptions,we introduce some new ideas.We also use the method of moving spheres instead of moving planes to obtain the explicit forms of the solutions more easily.Our result,therefore,improves and uni fies both results in[7]and[9].To state our first result,we denote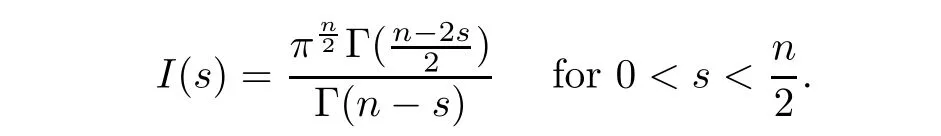

Theorem 1.1

Let 0

<α,β<n

and

f,g

∈

C

([0

,

∞)×[0

,

∞))be two nonnegative functions such that

for some

c

,c

,μ>

0 and

x

∈R.Moreover,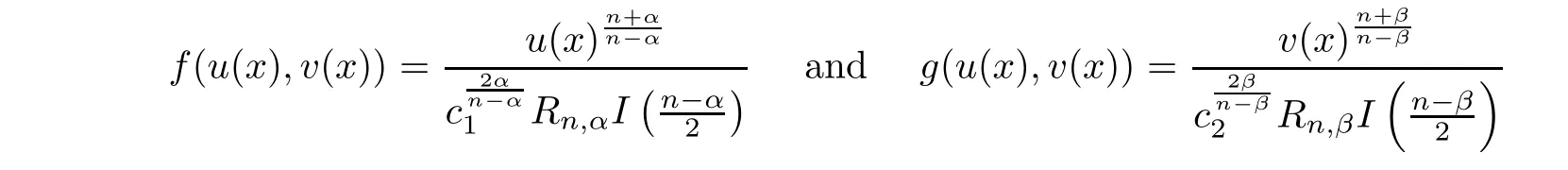

for all

x

∈R.

Remark 1.2

The assumption that

f

(

s,t

)is increasing in

t

and

g

(

s,t

)is increasing in

s

is to ensure that the system is non-degenerate.This non-degeneracy assumption was proposed in[4]and was also used in[9].Without this assumption,system(1.2)may contain two unrelated equations such as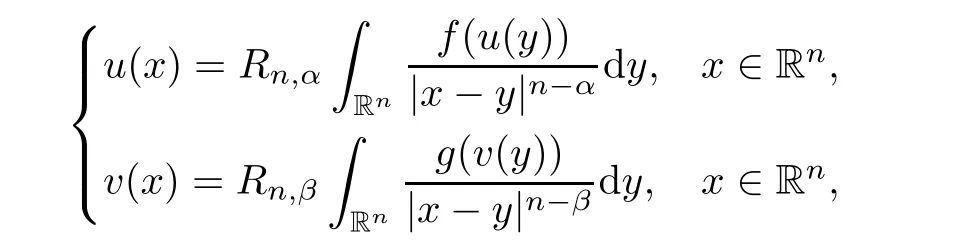

and hence

u,v

may not have the same symmetric center in such a case.

Remark 1.3

For the simplicity of the presentation,we only consider systems of two equations in this paper.However,our method can be extended to integral systems with more equations as in[9].

Next,we discuss the classification of nonnegative classical solutions of elliptic system(1.1).We first mention the case of a single equation.Several authors have contributed to a classification result stated that every nonnegative classical solution to the critical semilinear elliptic equation

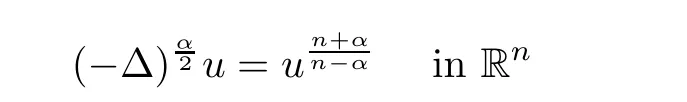
must assume the form

Some analogous results were established for system(1.1).Using the classical moving plane method,Guo and Liu[8]classified all nonnegative solutions of(1.1)when

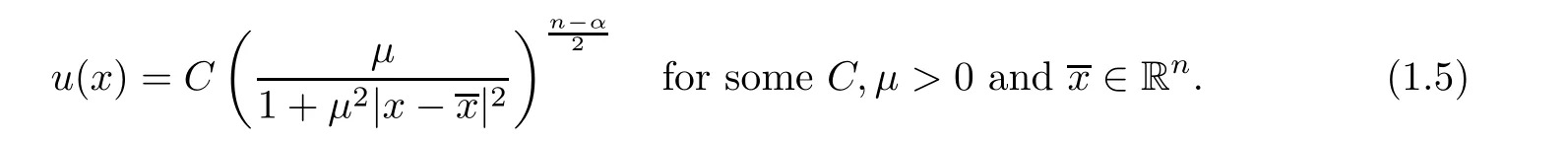
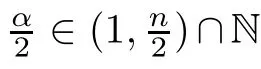
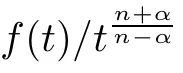
α

=

β

=2 and

f,g

satisfy some monotonicity conditions.Later,a fractional counterpart result was derived by Li and Ma[21]using the direct method of moving planes.More precisely,Li and Ma assumed that(

u,v

)is a nonnegative solution of(1.1)and?0

<α,β<

2,

f

(

s,r

)≡

f

(

r

),

g

(

r,t

)≡

g

(

r

),

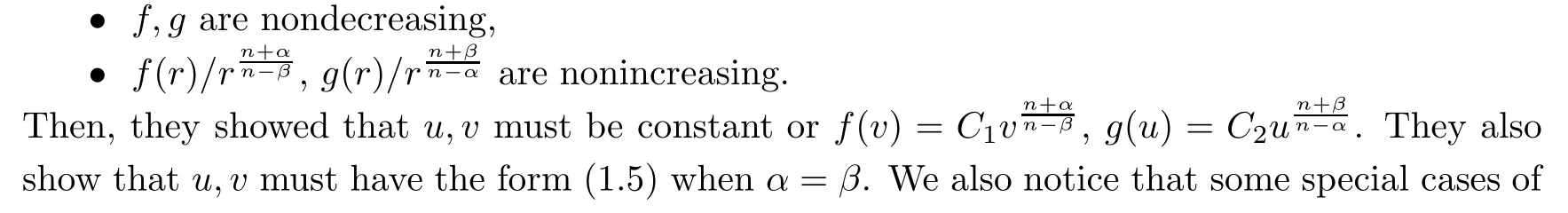
Theorem 1.4

Assume that

f

and

g

satisfy all assumptions of Theorem 1.1 and one of the following conditions holds: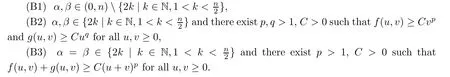

Assume that(

u,v

)is a nonnegative nontrivial classical solution of system(1.1).Then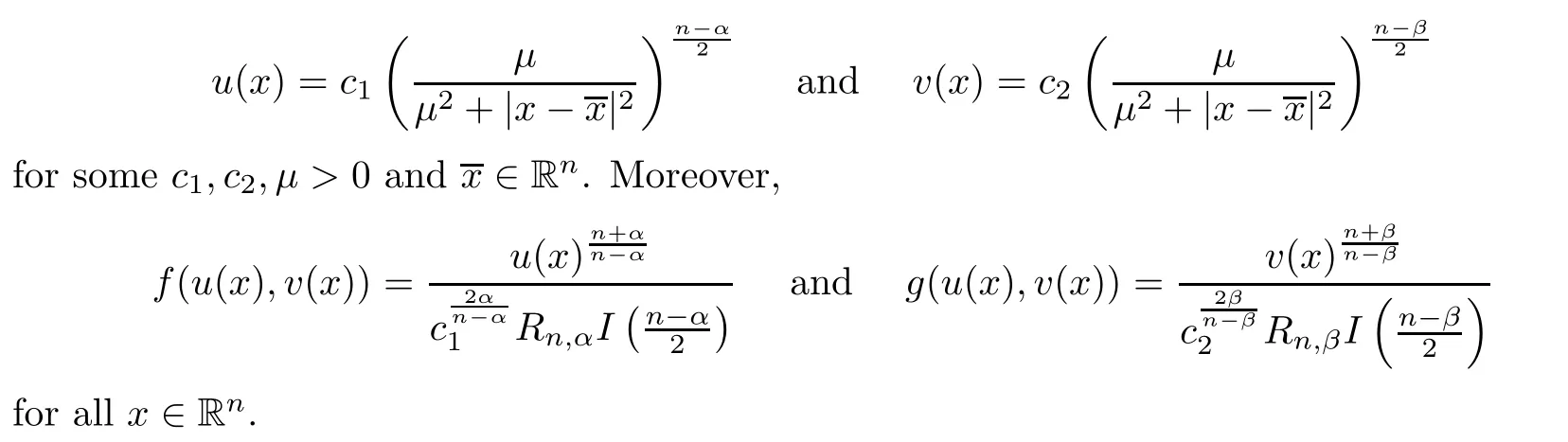

As a consequence of Theorem 1.4,we consider a situation where we can deduce the explicit forms of

f

and

g

.

(i)

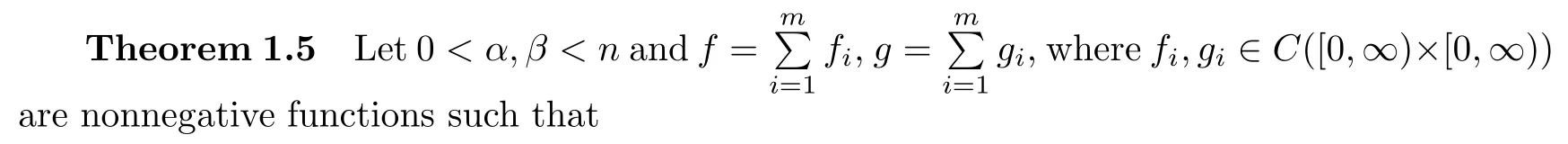
f

(

s,t

)is nondecreasing in

s

and increasing in

t

,(ii)

g

(

s,t

)is increasing in

s

and nondecreasing in

t

,(iii)For every

i

=1

,

2

,...,m

,there exist

p

,p

≥0,(

n

?

α

)

p

+(

n

?

β

)

p

=

n

+

α

such that

f

(

s,t

)

/

(

s

t

)is nonincreasing in each variable,(iv)For every

i

=1

,

2

,...,m

,there exist

q

,q

≥0,(

n

?

α

)

q

+(

n

?

β

)

q

=

n

+

β

such that

g

(

s,t

)

/

(

s

t

)is nonincreasing in each variable.Assume that(

u,v

)∈

C

(R)×

C

(R)is a nonnegative nontrivial solution of system(1.2).Then

for some

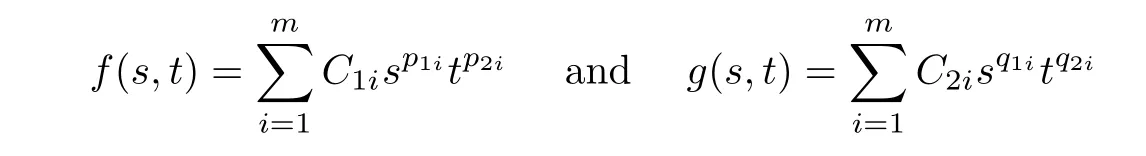
c

,c

,μ>

0 and

x

∈R.Moreover,for all(

s,t

)∈[0

,

max

u

]×[0

,

max

v

],where

C

,C

>

0 satisfy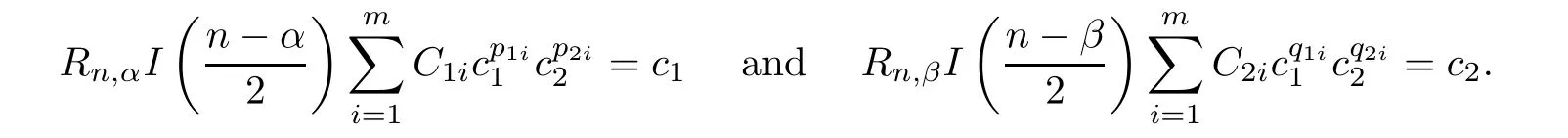

The same conclusion also holds for every nonnegative nontrivial classical solution(

u,v

)of system(1.1)if we further assume that(B1),(B2),(B3)are satis fied.

Remark 1.6

Theorem 1.5 extends[7,Theorem 4]to the case

α

/=

β

.Some special cases of the last statement of Theorem 1.5 were previously proved in[8](when

α

=

β

=2)and[21](when 0

<α,β<

2).

In particular,Theorem 1.5 can be applied to the system

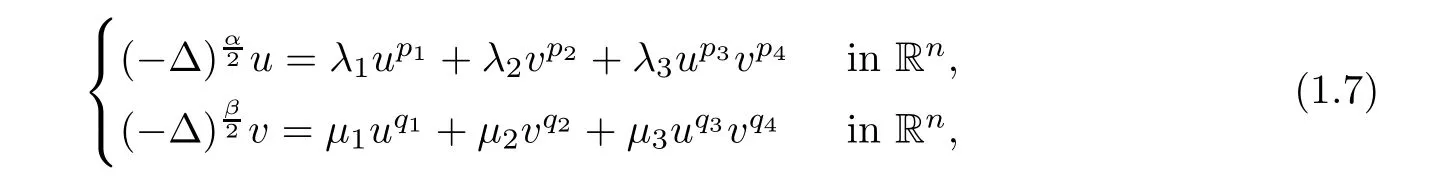
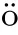
We can state the following corollary of Theorem 1.5,which improves[5,22,29].

Assume that(

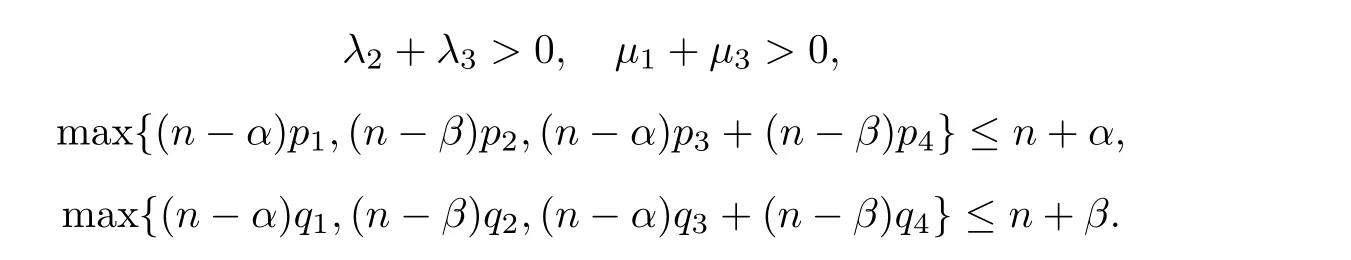
u,v

)is a nonnegative nontrivial classical solution of system(1.7).Then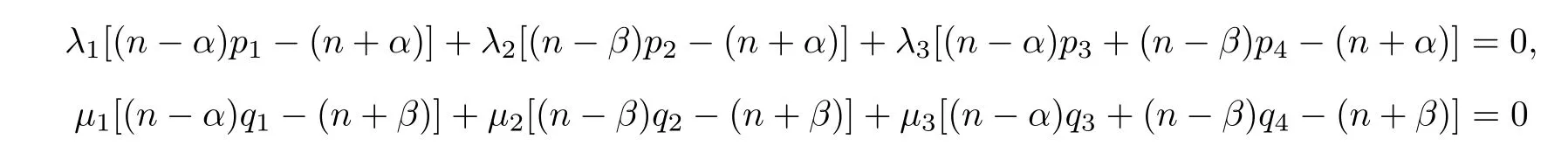

and(

u,v

)assumes the form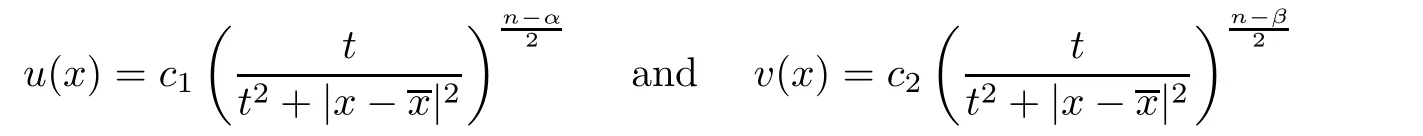

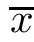
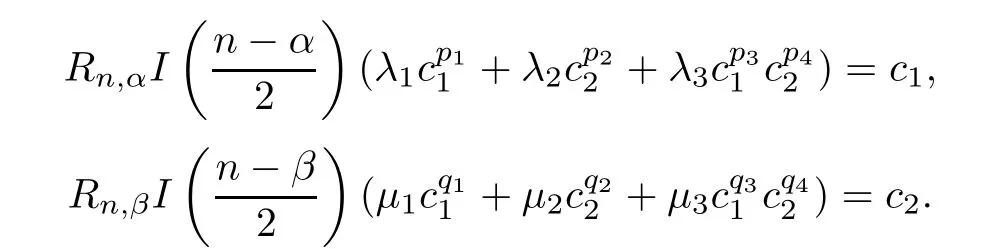
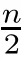
The remainder of this paper is organized as follows:in Section 2,we use the method of moving spheres to prove Theorem 1.1.In Section 3,we establish the equivalence between system(1.1)and system(1.2),then Theorem 1.4 follows immediately.The last section is devoted to the proof of Theorem 1.5,which is concerned with a special case,where

f

and

g

can be explicitly derived.Throughout this paper,we denote by

B

(

x

)the ball of radius

R>

0 with center

x

∈R.For brevity,we will write

B

=

B

(0).We also use

C

to denote various positive constants whose values may change from place to place.

2 Classification of Nonnegative Solutions to the Integral System

To prove Theorem 1.1,we employ the method of moving spheres in integral forms.It is different from the moving plane method used by other authors we mentioned in the introduction section.The method of moving spheres was introduced by Li and Zhu[30].Lately,Li and Zhang[31]and Li[32]improved Li and Zhu’s two calculus key lemmas.An advantage of this method is that it can immediately yield the explicit form of solutions to elliptic equations satisfying certain conformal invariance and the nonexistence to elliptic equations with subcritical exponent.Hence it is not necessary to prove the symmetry of solutions beforehand as in the method of moving planes.

Since we do not assume that

f,g

are differentiable,we cannot use the mean value theorem to obtain integral estimates as in[4,9].Our new idea is to exploit the following inequality in our later estimation:

Lemma 2.1

Assume that

f

satis fies(A1).Then for all

t

>t

>

0 and

s>

0,we have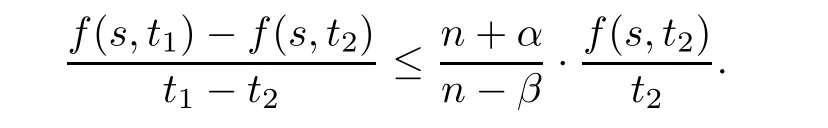

Similarly,for all

t>

0 and

s

>s

>

0,we have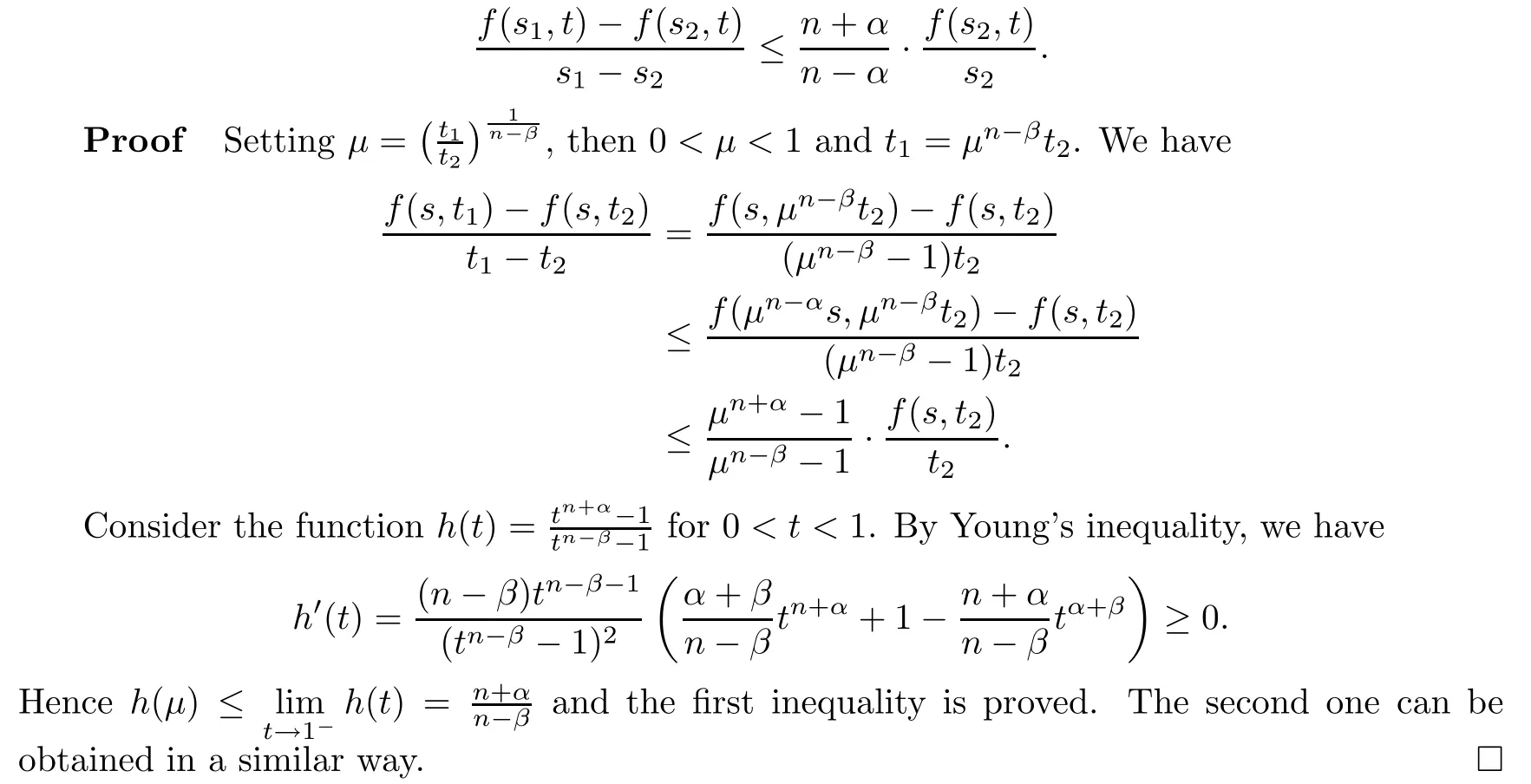

In what follows,let(

u,v

)∈

C

(R)×

C

(R)be a nonnegative nontrivial solution of system(1.2).Then,it follows that

u

and

v

are positive.For any

x

∈Rand

λ>

0,we denote by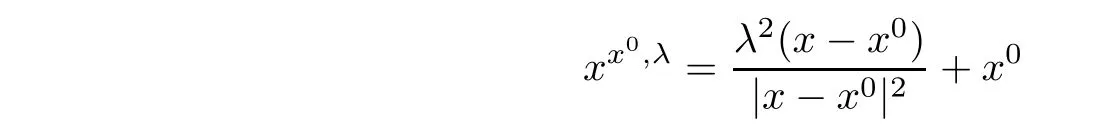

the inversion of

x

∈R{

x

}about the sphere

?B

(

x

).Then,we de fine the Kelvin transform of

u

and

v

with respect to

?B

(

x

)by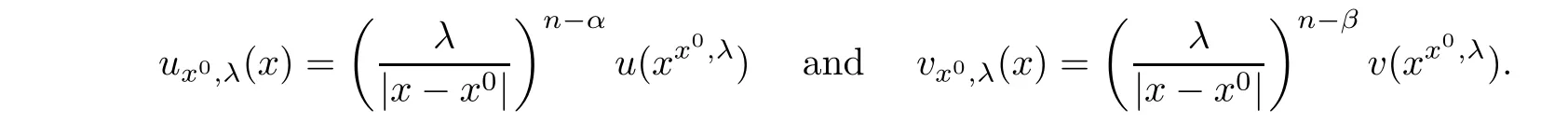

We also de fine

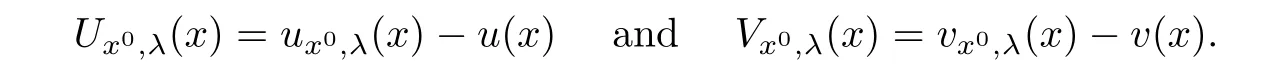
We will use the method of moving spheres in integral forms to prove the following proposition:

Proposition 2.2

For any

x

∈R,the set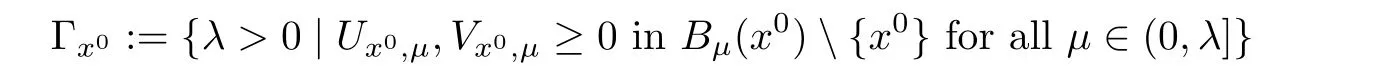

is not empty.Moreover,if

λ

:=supΓ

<

∞,then

U

=

V

=0 in

B

(

x

){

x

}.Since system(1.2)is invariant by translations,it suffices to prove Proposition 2.2 for

x

=0.For the sake of simplicity,we will drop the subscript

x

in the notations when

x

=0.That is,we will write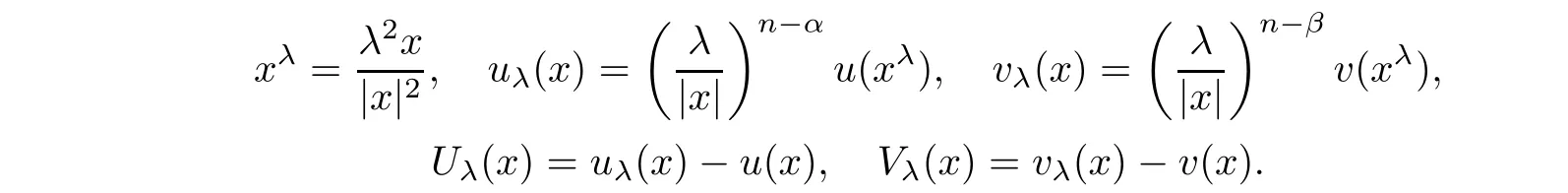

We first remark that(

u

,v

)satis fies,for all

x

∈R{0},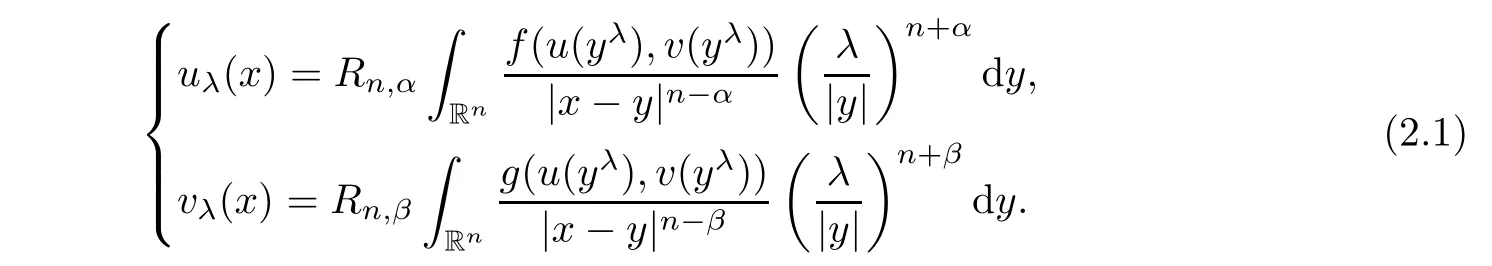

Indeed,using the first equation in(1.2),we have

for any

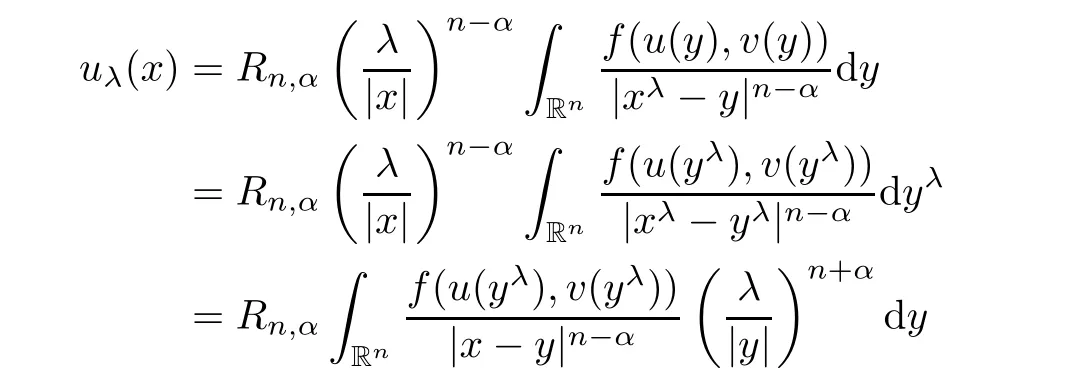
x

∈R{0},where we have used the following identities in the last line: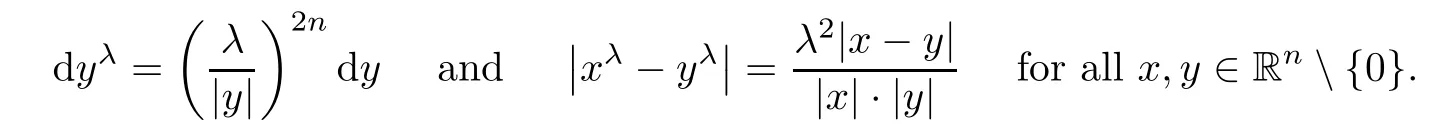

The second equation in(2.1)can be obtained in the same way.

Next,for each

λ>

0,we denote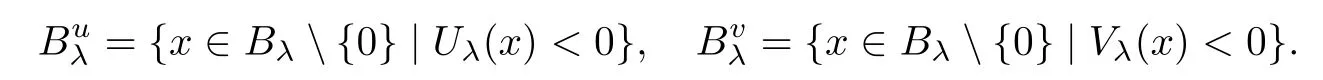

We prove key integral estimates which will be used in the proof of Proposition 2.2.

Lemma 2.3

If 0

<λ<λ

,then there exists

C>

0,which depends on

λ

but is independent of

λ

,such that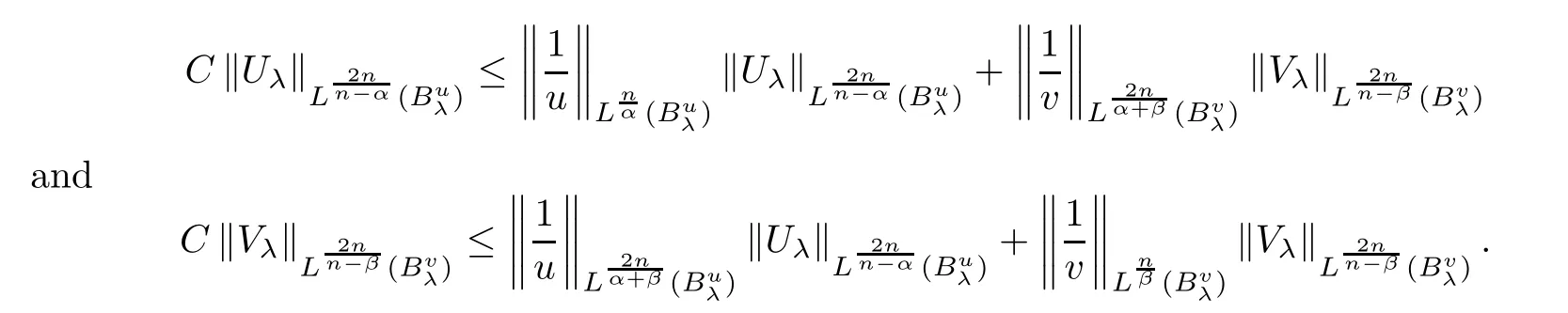

Proof

Let any

x

∈

B

{0}.From the first equation in(1.2),we have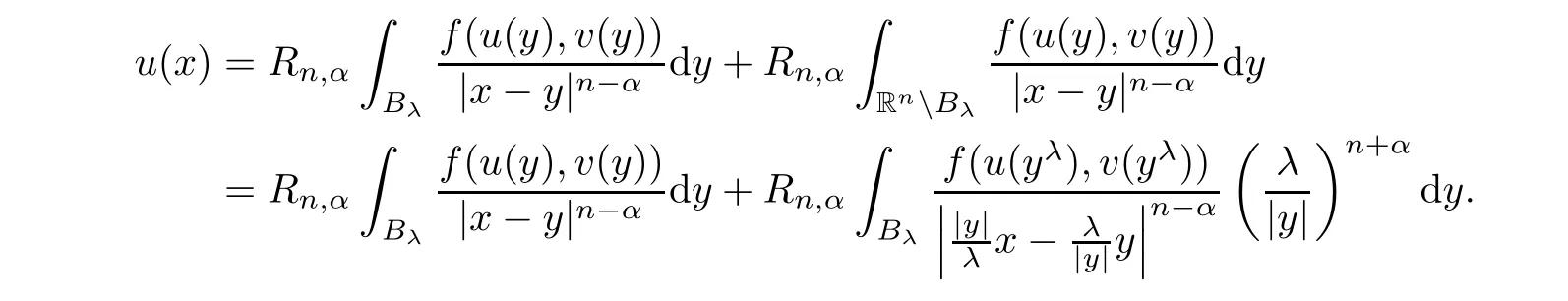

Similarly,from the first equation in(2.1),we obtain

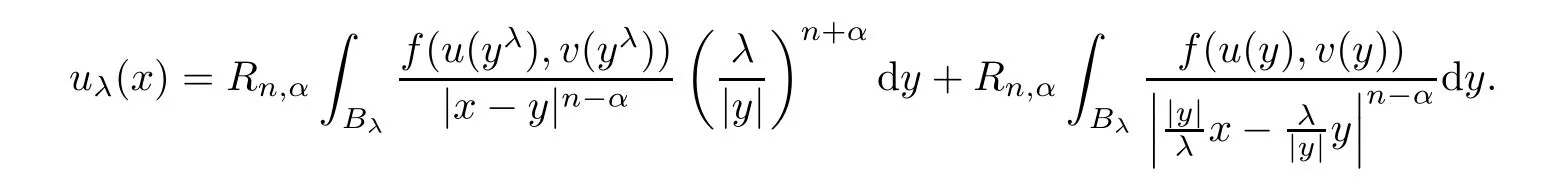
Combining the above two formula,we derive

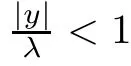
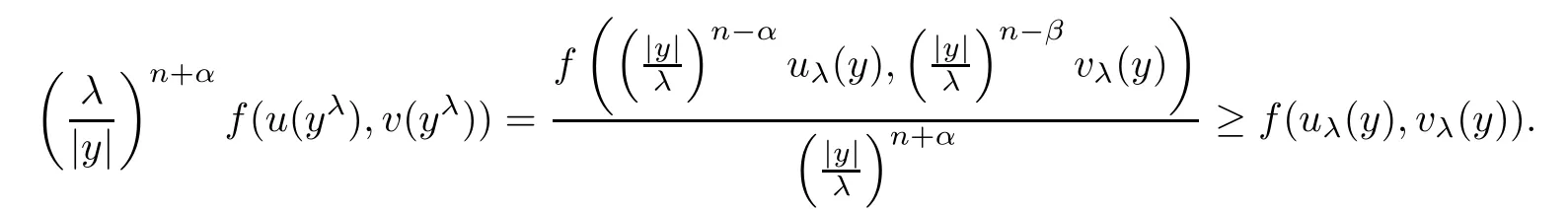
Combining this with(2.2)and(2.3),we obtain

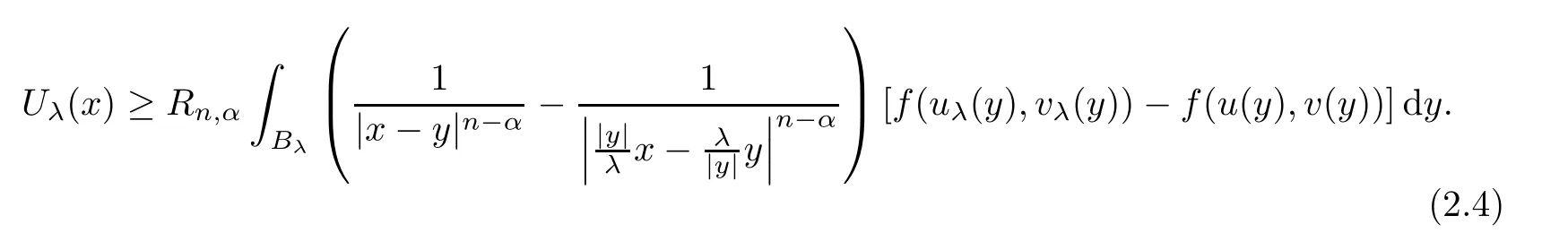
Using Lemma 2.1,we have

If

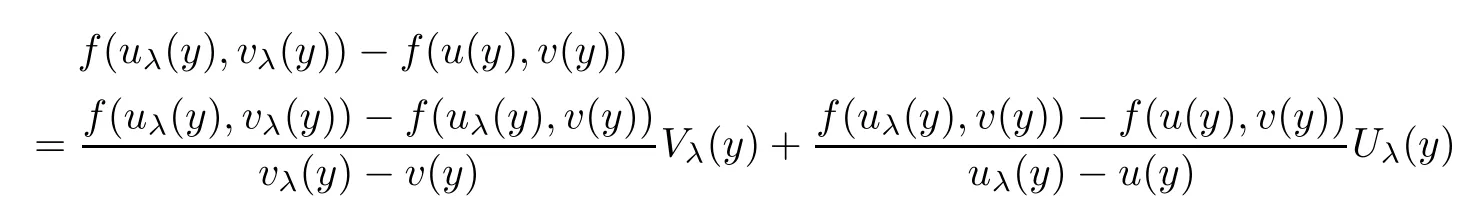
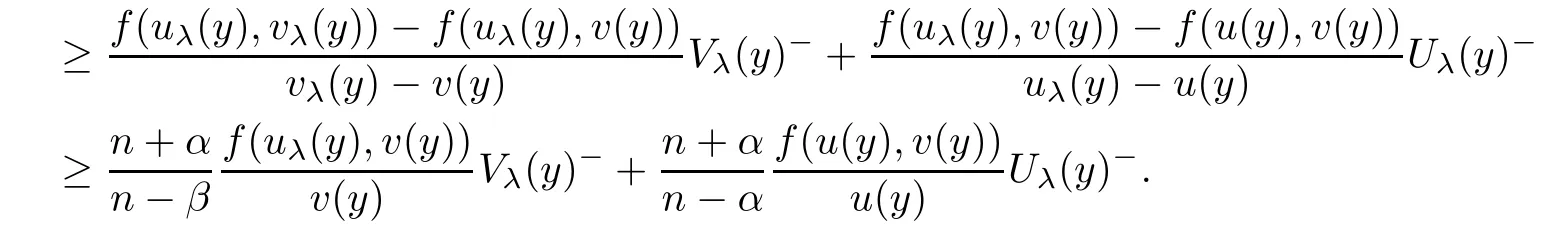
u

(

y

)

<u

(

y

),then from the above inequality,we have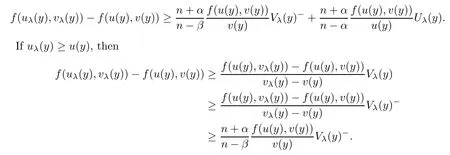

Therefore,in both cases,we have,for any

y

∈

B

{0},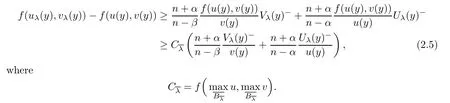

From(2.4),(2.3)and(2.5),we deduce

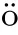
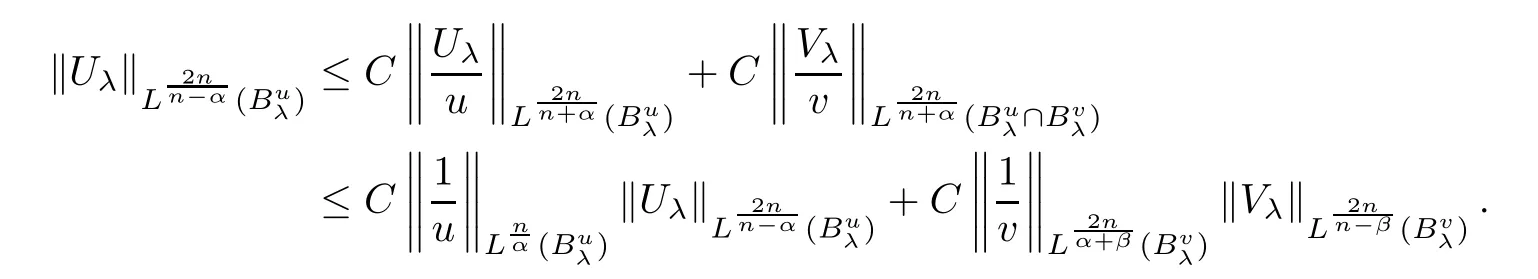
The second inequality can be derived in a similar way.

Proof of Proposition 2.2

As mentioned before,we only need to prove the proposition for

x

=0.

Step 1

(Start dilating the sphere

?B

from near

λ

=0)In this step,we prove that Γ/=?,that is,for

λ>

0 sufficiently small,

Indeed,since

u

and

v

are continuous and positive,there exists

ε

∈(0

,

1)small enough,such that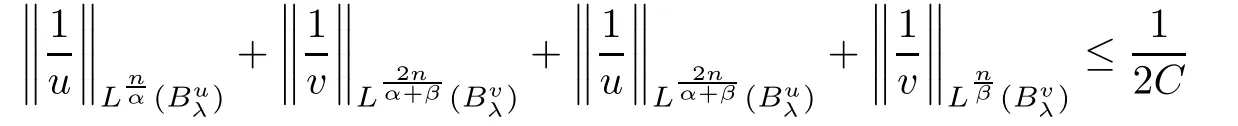

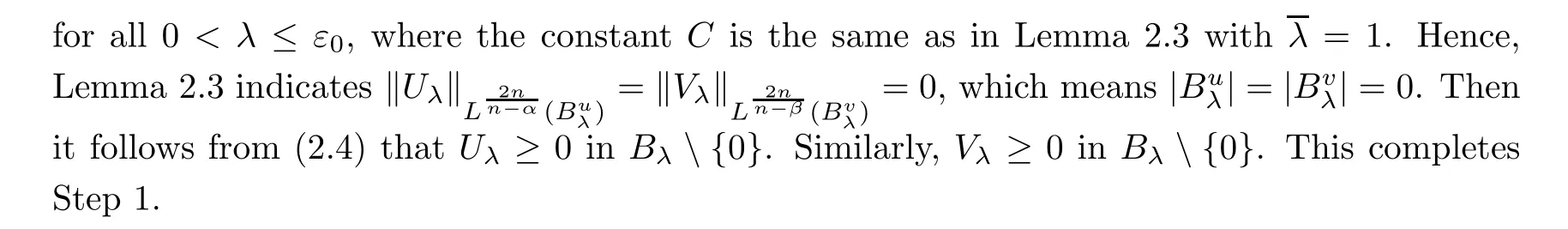
Step 2

(Dilate the sphere

?B

outward to the limiting position)Step 1 provides us a starting point to dilate the sphere

?B

from near

λ

=0.Now we dilate the sphere

?B

outward as long as(2.6)holds.Let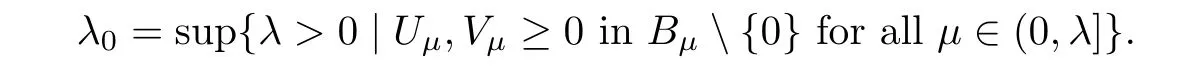

In this step,we show that

By contradiction,we assume

λ

<

∞and

V

/≡0 in

B

{0}.Since

U

,V

are continuous with respect to

λ

,we already have

U

,V

≥0 in

B

{0}.From(2.4),we have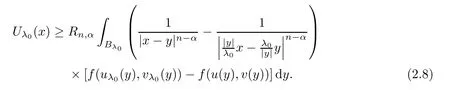

This implies

U

>

0 in

B

{0}.Then using a similar reasoning,we have

V

>

0 in

B

{0}.Next,we claim that there exists

C>

0 and

η>

0 such that

Indeed,from(2.8)and Fatou’s lemma,we have

Hence for

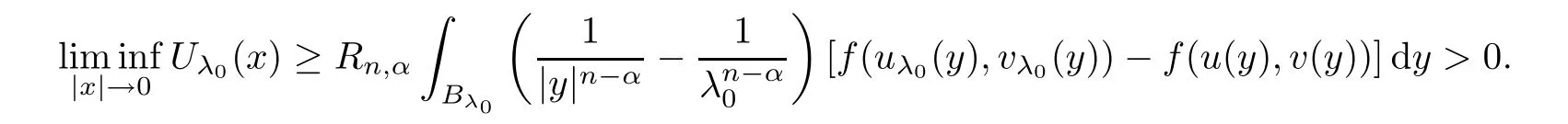
x

∈

B

{0},where

η

is sufficiently small,we have

U

(

x

)≥

C

.Similarly,for

x

∈

B

{0},where

η

is chosen smaller if necessary,we also have

V

(

x

)≥

C

.This proves(2.9).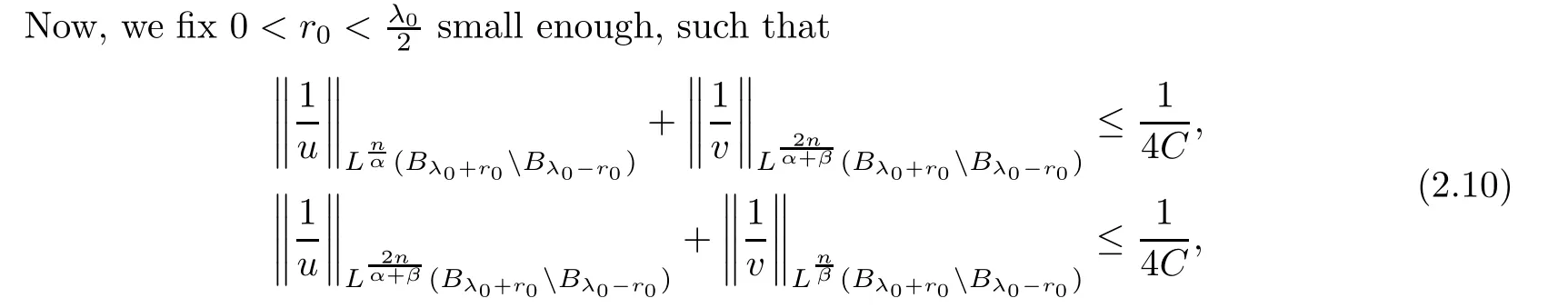

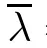
From(2.9),and the continuity and positivity of

U

and

V

,we can find a constant

C>

0 such that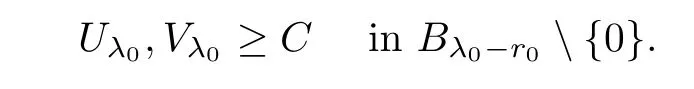

Since

u

and

v

are uniformly continuous on an arbitrary compact set,there exists

ρ

∈(0

,r

)such that,for any

λ

∈(

λ

,λ

+

ρ

),

Therefore,for any

λ

∈(

λ

,λ

+

ρ

),

However,this contradicts the de finition of

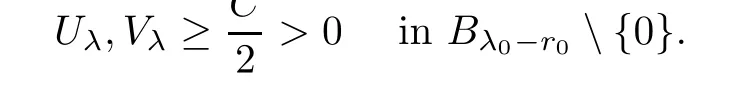
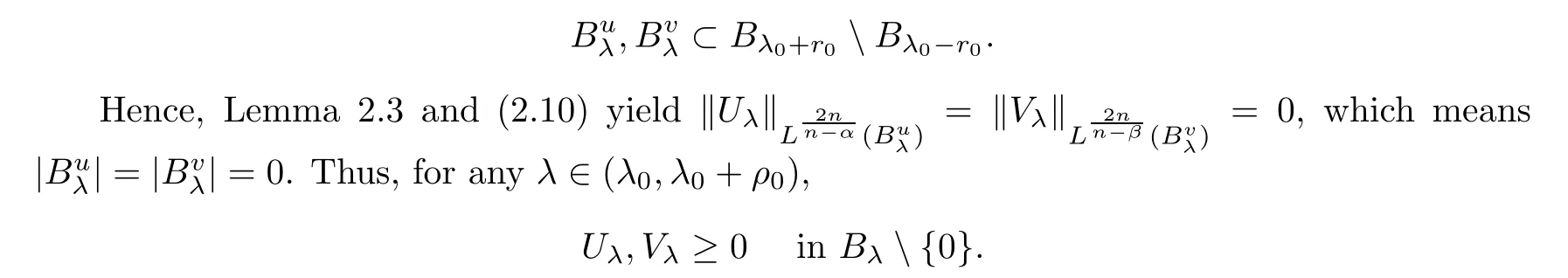
λ

and(2.7)is proved.

This completes the proof of Proposition 2.2.

To obtain explicit forms of all nonnegative solutions of(1.2),we need the following calculus lemma:

Lemma 2.4

(See Appendix B in[32])Let

n

≥1,

ν

∈R and

w

∈

C

(R).For every

x

∈Rand

λ>

0,we de fine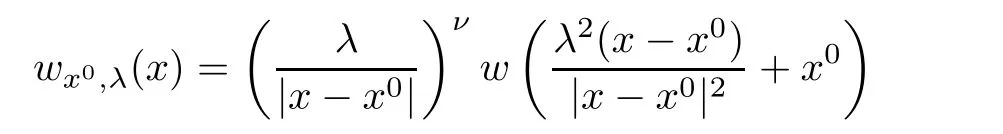

for all

x

∈R{

x

}.Then,we have the following:(i)If for every

x

∈R,there exists

λ

<

∞such that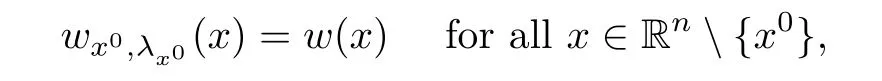

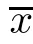
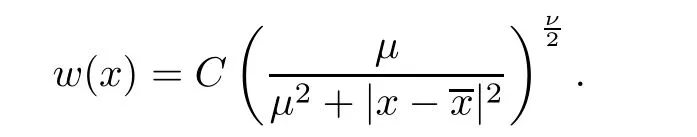
(ii)If for every

x

∈R,

then

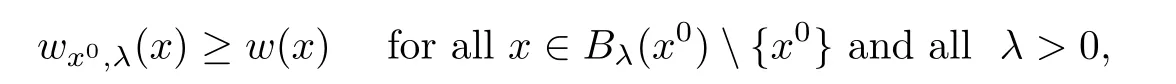
w

≡

C

for some constant

C

∈R.

Remark 2.5

If case(i)of Lemma 2.4 happens,then a direct computation yields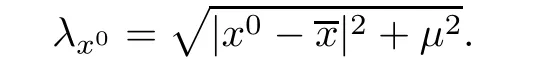

We are ready to prove the main result in this section,namely,Theorem 1.1.

Proof of Theorem 1.1

There are three cases.

Case 1

There exist

x

,y

∈Rsuch that

λ

=∞and

λ

<

∞.Since

λ

=∞,we have,for any

λ>

0,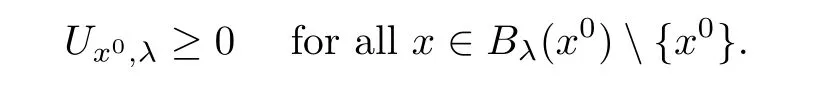

This implies that,for any

λ>

0,

Due to the arbitrariness of

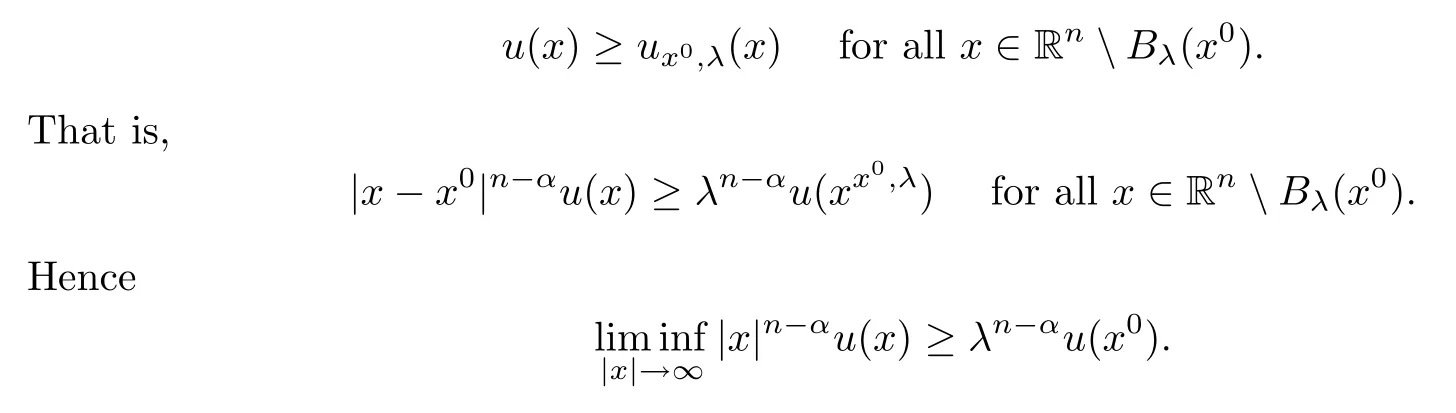
λ>

0,we must have

On the other hand,since

λ

<

∞,we may use Proposition 2.2 to get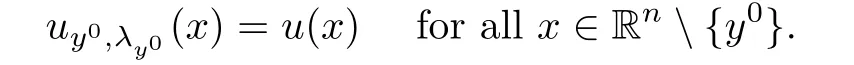

This indicates that

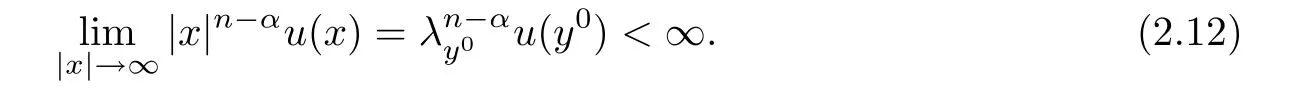
The contradiction between(2.11)and(2.12)indicates that Case 1 cannot happen.

Case 2

For every

x

∈R,the critical scale

λ

=∞.By Lemma 2.4(ii)and the positivity of

u

and

v

,we have(

u,v

)≡(

C

,C

)for some constants

C

,C

>

0.This is absurd since positive constant functions do not satisfy(1.2).

Case 3

For every

x

∈R,the critical scale

λ

<

∞.

From Proposition 2.2,we have

Using Lemma 2.4(i)and Remark 2.5,we deduce that(

u,v

)must assume the form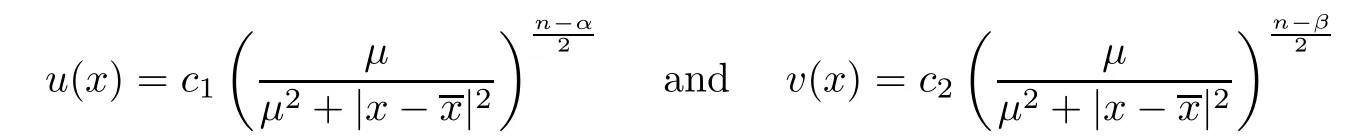

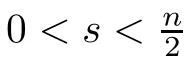
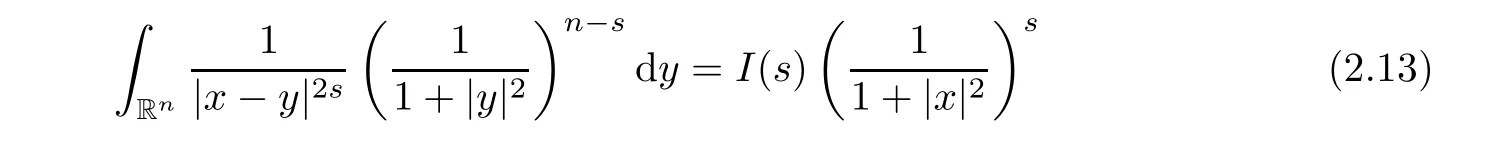
(see(37)in[33]).Using(2.13),we obtain

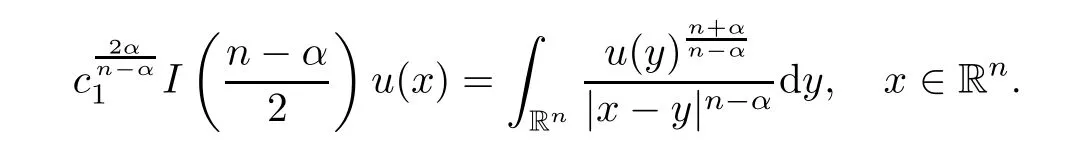
Hence,we deduce

Similarly,

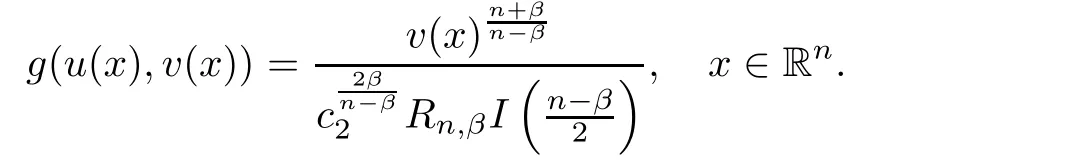
This completes the proof of Theorem 1.1.

3 Classification of Nonnegative Solutions to the System of PDEs

We exploit the ideas in[2]to establish the equivalence of systems(1.1)and(1.2).Then,we prove Theorem 1.4 in this section.

Proposition 3.1

Let

f,g

∈

C

([0

,

∞)×[0

,

∞))be two nonnegative functions and assume that either assumption(B1),(B2)or(B3)of Theorem 1.4 is satis fied.Suppose that(

u,v

)is a nonnegative classical solution of(1.1),then(

u,v

)is also a nonnegative solution of(1.2),and vice versa.

Proof

Suppose that(

u,v

)is a nonnegative classical solution of(1.1).Then,(

u,v

)satis fies the super polyharmonic property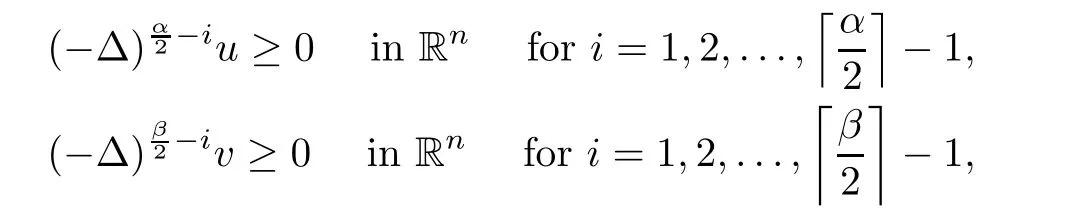

where「

t

?denotes the smallest integer which is not smaller than

t

.

Indeed,such the property was proved in[15,Theorem 1.1]if(B1)holds,in[26,Theorem 2]if (B2)holds and in[26,Theorem1]if(B3)holds.

If

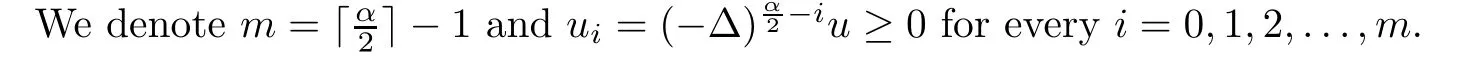
n

=2,then

m

=0 and we can go directly to Case 2 below.Hence,in deriving form ulae(3.1)below,we may assume

n

≥3.We observe that

u

is a nonnegative solution of the equation??

u

=

u

=

f

(

u,v

)in R.For any

R>

0,let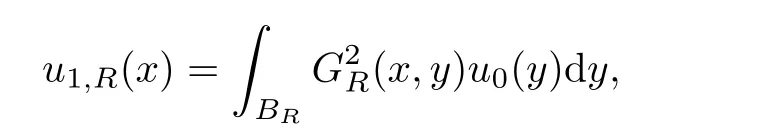

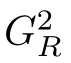
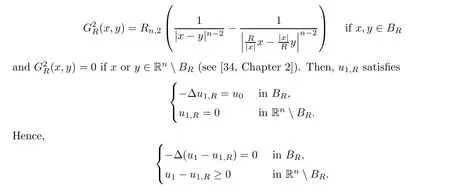
From the maximum principle,we have

for any

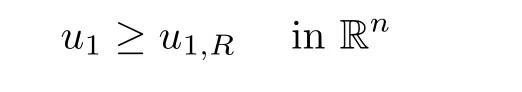
R>

0.For each fixed

x

∈R,letting

R

→∞,we obtain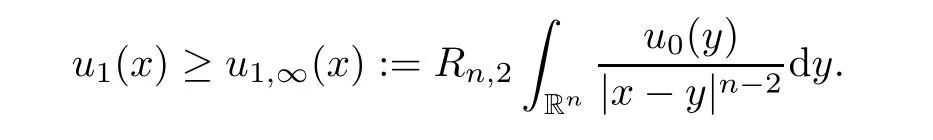

Remark that

u

satis fies??

u

=

u

in R.Hence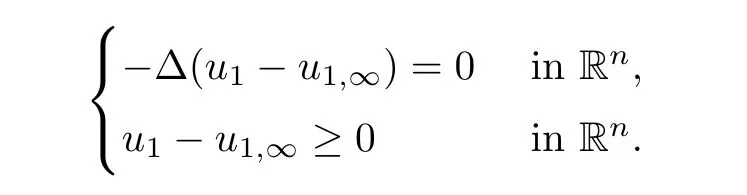

From the Liouville theorem for harmonic functions,we can deduce that

u

?

u

≡

C

≥0.That is,

In the same way,using the fact that

u

is a nonnegative solution of the equation??

u

=

u

in Rfor

i

=1

,

2

,...,m

,we deduce that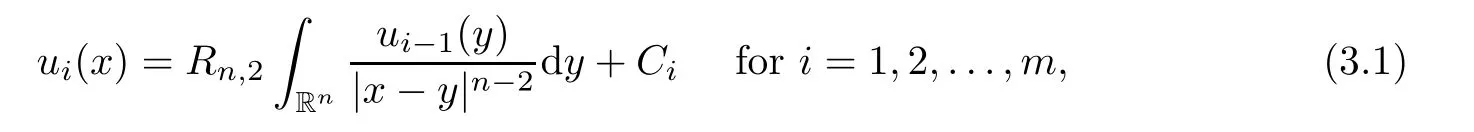

where

C

≥0.Now we set

γ

=

α

?2

m

,then

γ

∈(0

,

2].We consider two cases.

Case 1

γ

=2In this case,

u

is a nonnegative solution of the equation??

u

=

u

in R.Hence we can use the above argument to obtain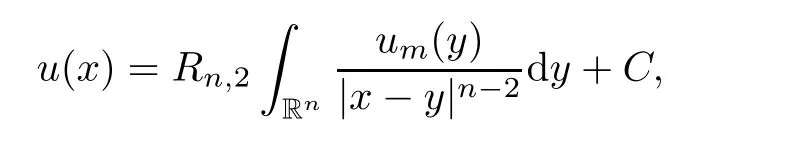

where

C

≥0.

Case 2

γ

∈(0

,

2)In this case,

u

is a nonnegative solution of the fractional equation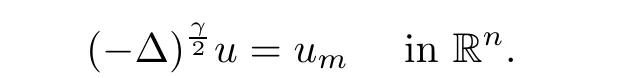

For any

R>

0,let

By the maximum principle for

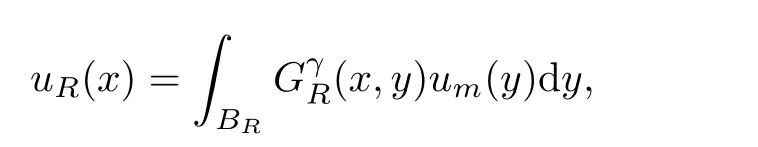
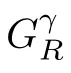
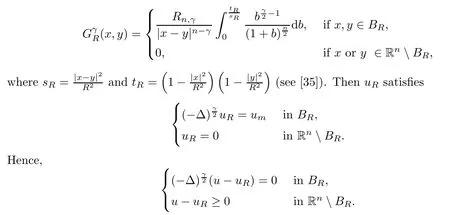
γ

-superharmonic functions(see[1,14]),we deduce that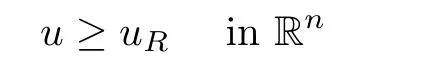

for any

R>

0.For each fixed

x

∈R,letting

R

→∞,we have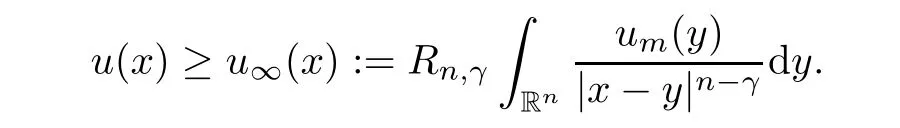

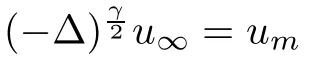
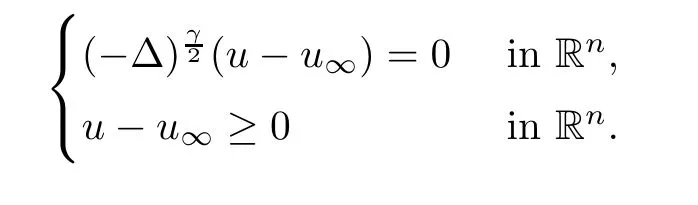
From the Liouville theorem for

γ

-harmonic functions(see[25]),we can deduce that

u

?

u

≡

C

≥0.That is,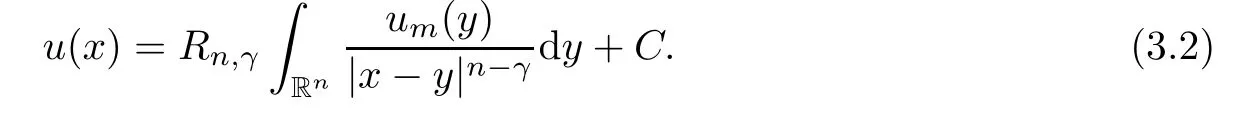

Hence,in all cases,we have the formula(3.1)(if

m>

0)and(3.2).Moreover,we must have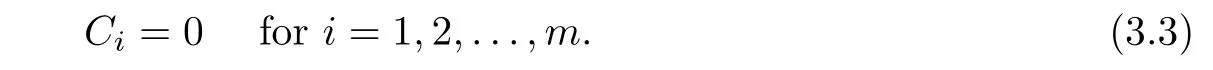

Indeed,if

C

>

0 for some

i

∈{1

,

2

,...,m

?1},then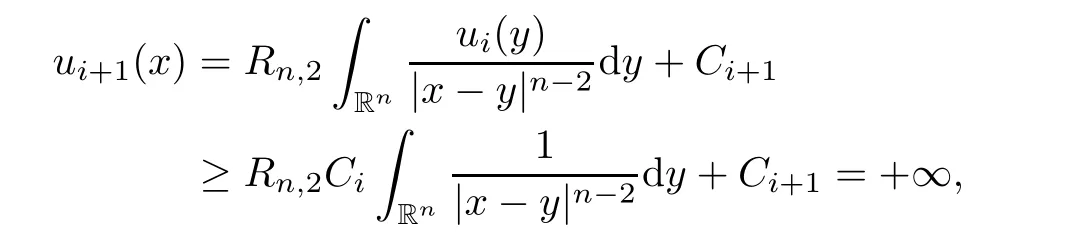

which is a contradiction.Similarly,if

C

>

0,then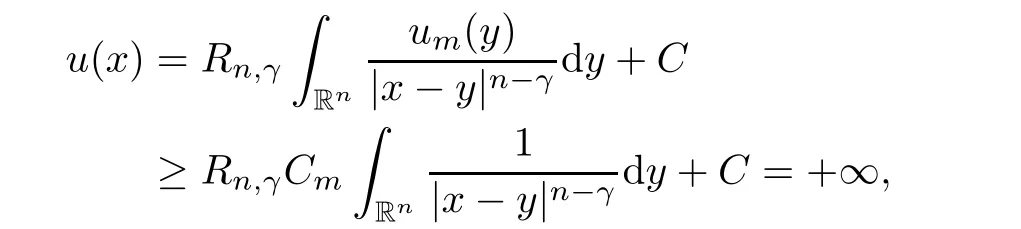

which is also absurd.

From(3.1),(3.2)and(3.3),we deduce

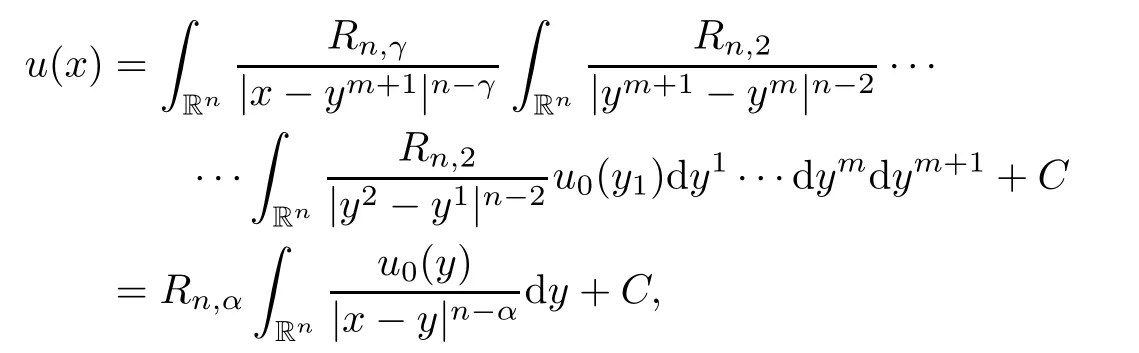
where in the last equality,we have used Fubini’s theorem and the following Selberg formula:

for any

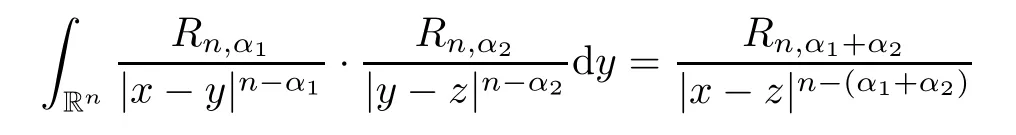
α

,α

∈(0

,n

)such that

α

+

α

∈(0

,n

)(see[36]).

We have proved that

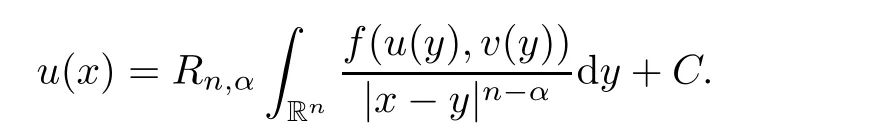
Similarly,

where

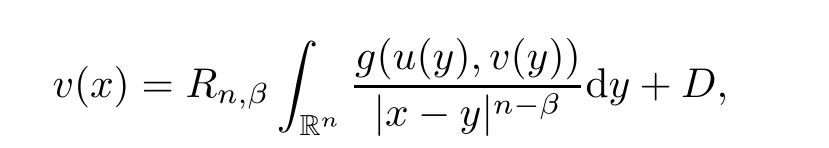
D

≥0.We claim that

C

=

D

=0.Otherwise,suppose

C>

0,then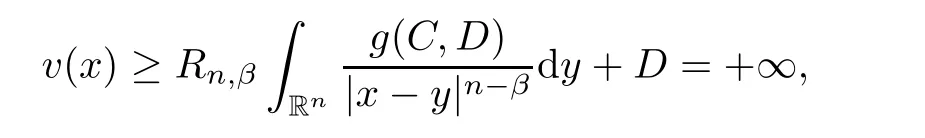

which is absurd.Hence

C

=

D

=0 and(

u,v

)is a nonnegative solution of(1.2).Conversely,assume that(

u,v

)satis fies(1.3)and(

u,v

)is a nonnegative solution of(1.2).We have

That is,(

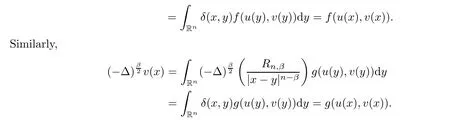
u,v

)is a nonnegative solution of(1.1).

Proof of Theorem 1.4

Theorem 1.4 is a direct consequence of Theorem 1.1 and Proposition 3.1.

4 A Special Case

In this section,we prove Theorem 1.5.Basically,it is a consequence of Theorem 1.1 and Proposition 3.1.

Proof of Theorem 1.5

Let(

u,v

)∈

C

(R)×

C

(R)be a nonnegative nontrivial solution of system(1.2).Then

u,v>

0.For each

i

=1

,

2

,...,m

,we de fine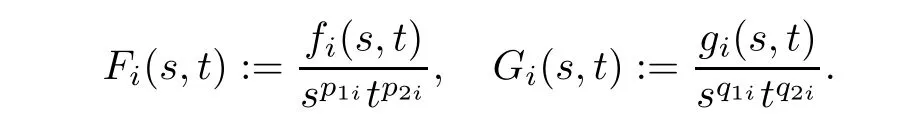

Then,

F

,G

are nonincreasing in each variable.Notice that for all

s,t

≥0,

μ>

0,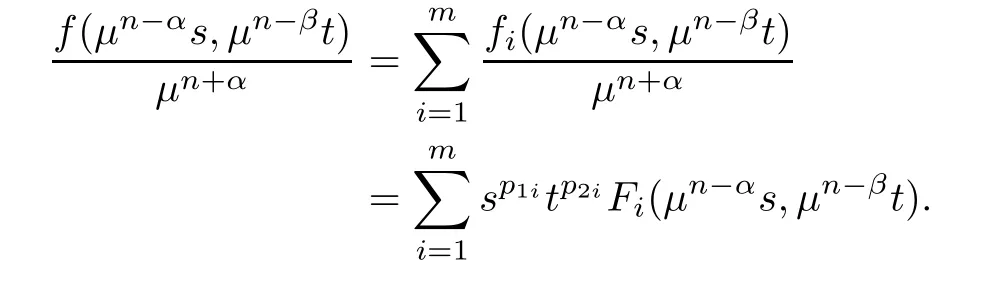

Hence,

f

satis fies(A1).By a similar reasoning,we see that

g

satis fies(A2).Therefore,by applying Theorem 1.1,we deduce that(

u,v

)must have the form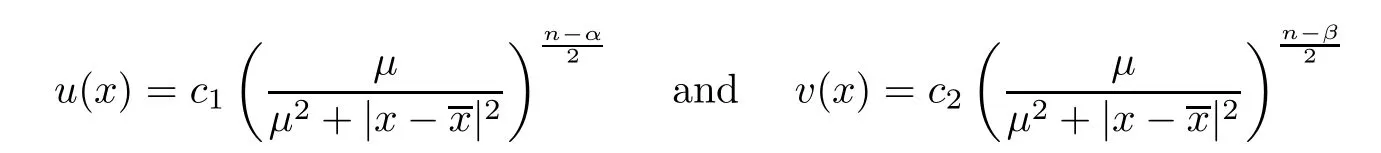

for some

c

,c

,μ>

0 and

x

∈R.Moreover,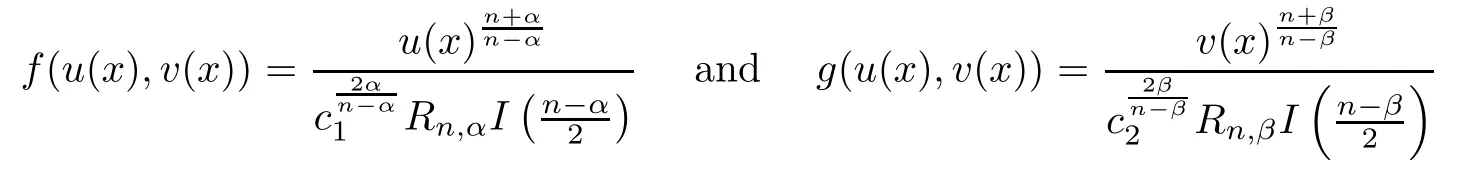

for all

x

∈R.Hence

for all

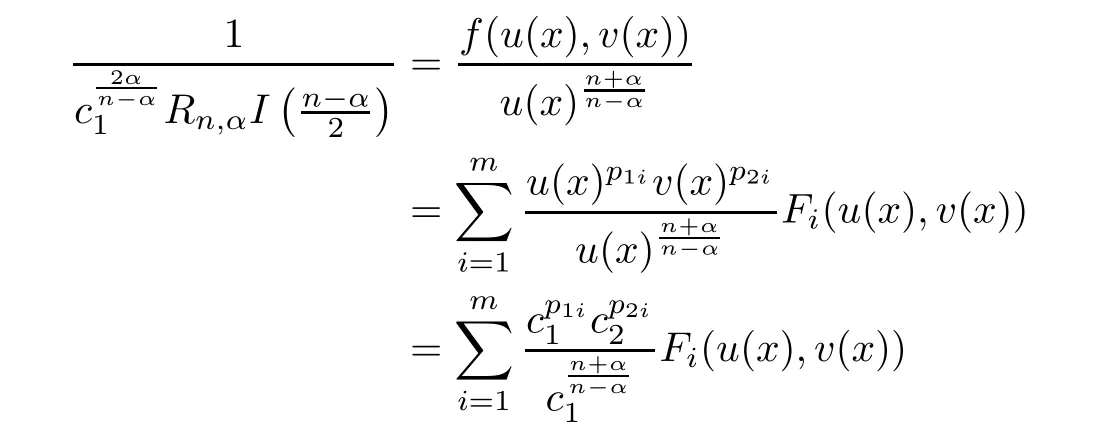
x

∈R.Using the assumption that all

F

are nonincreasing in each variable and the fact that

u,v

decay at in finity and attain their maximums at

x

,we conclude that

F

(

s,t

)=

C

for all(

s,t

)∈[0

,

max

u

]×[0

,

max

v

],

i

=1

,

2

,...,m

,where positive constants

C

satisfy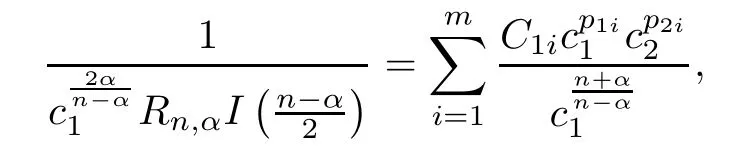

which means

In a similar way,we can show that

G

(

s,t

)=

C

for all(

s,t

)∈[0

,

max

u

]×[0

,

max

v

],where

C

>

0 and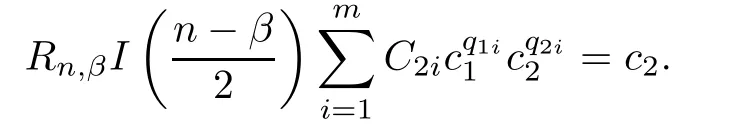

Therefore,

f

and

g

have the desired forms.The first part of the theorem is proved.Now we assume that(

u,v

)is a nonnegative nontrivial classical solution of system(1.1)and(B1),(B2),(B3)are satis fied.In this situation,we may use Proposition 3.1 to deduce that(

u,v

)is a nonnegative solution of(1.2).Then,we can derive the same conclusion as above.