THE GROWTH AND BOREL POINTS OF RANDOM ALGEBROID FUNCTIONS IN THE UNIT DISC?
(孫道椿)
School of Mathematics,South China Normal University,Guangzhou 510631,China E-mail:1457330943@qq.com
Yingying HUO (霍穎盈)
School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China E-mail:huoyingy@gdut.edu.cn
Fujie CHAI (柴富杰)?
School of Financial Mathematics&Statistics,Guangdong University of Finance,Guangzhou 510521,China E-mail:chaifujie@sina.com
Abstract In this paper,we construct k-valued random analytic algebroid functions for the first time.By combining the properties of random series,we study the growth and Borel points of random analytic algebroid functions in the unit disc and obtain some interesting theorems.
Key words Sequence of random variables;algebroid functions;growth;Borel points
1 Introduction and results
In 1948,J.E.Littlewood and A.C.Offord discussed the“pit behaviour”of random integral functions with a Rademacher squence([4]).M.N.Mikhail later obtained some analogous results on random meromorphic functions in the complex plane([5]).In[8],D.C.Sun and J.R.Yu studied some random Dirichlet series with wider assumptions in the half plane and proved that all the points on the imaginary axis are the Borel points almost surely(a.s.).In 2009,D.C.Sun investigated the growth and Borel points of some random meromorphic functions in the unit disc and obtained some interesting theorems(see[9]).In the 1930s,the Nevanlinna value distribution theory for meromorphic functions(see[1,14])was extended to algebroid functions by H.Selberg([6]),E.Ullrich([12])and G.Valiron([13]).The natural question arises:how can we de fine random algebroid functions and discuss their properties of growth and Borel values or points?In this paper,we give the de finition ofk
-valued random algebroid functions for the first time,and prove that for those random algebroid functions,every point on the unit circle is a Borel point a.s..Unless otherwise speci fied,the reader can refer to[1,2,7,14]for the notation and terminology used in this paper.
Suppose thatA
(z
),A
(z
),...,A
(z
)are analytic functions in the unit disc{|z
|<
1}.Ψ(z,W
)is a bivariate complex function satisfying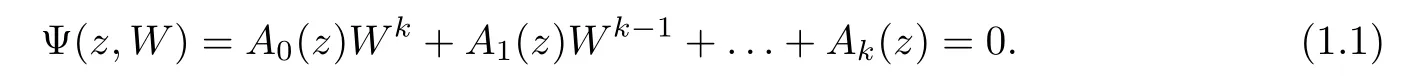
z
∈{|z
|<
1},the equation Ψ(z,W
)hask
complex rootsw
(z
),w
(z
),...,w
(z
).Then equation(1.1)de fines ak
-valued algebroid functionW
(z
).If,for allz
∈{|z
|<
1},we haveA
(z
)/=0,thenW
(z
)is an analytic algebroid function,and we can divide both sides of(1.1)byA
(z
).Hence,the analytic algebroid function has the form
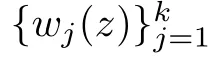
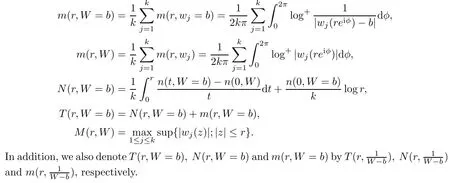
De finition 1.1
Suppose thatn
(r
)is a non-negative real valued function in(0,
1).The order ofn
(r
)is de fined as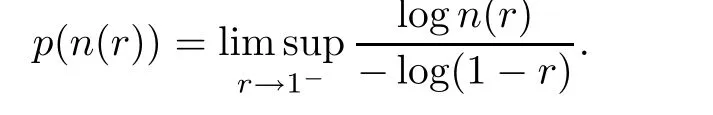
Remark 1.2
Suppose thatW
(z
)is ak
-valued algebroid function in the unit disc.The order ofW
(z
)is de fined as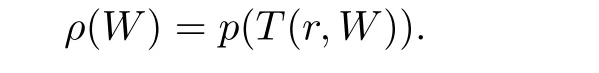
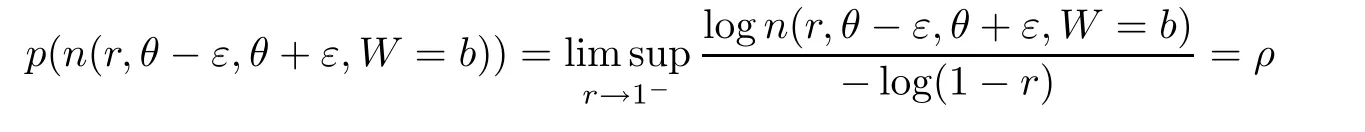
De finition 1.4
Forz
∈{|z
|<R
},we de fineμ
(r,A
)as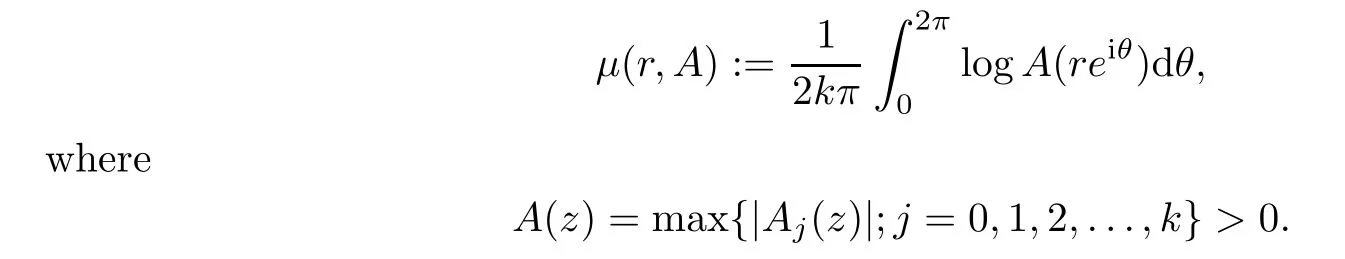
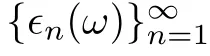

N
-sequence in[8].We de fine thek
random Taylor seriesA
(z,ω
)as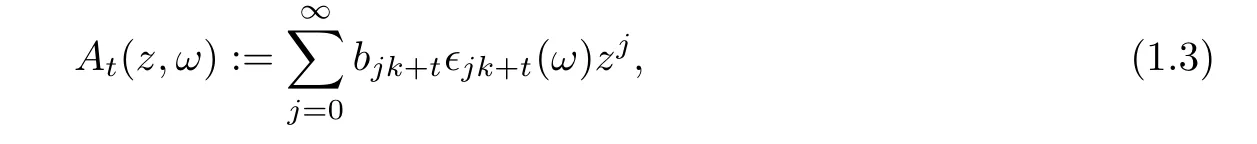
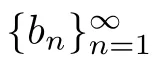
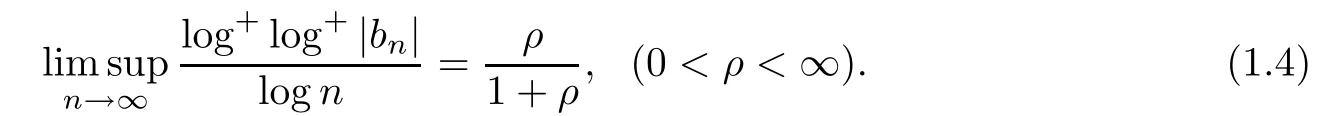
t
∈{1,
2,...,k
?1},sayt
=1,
such that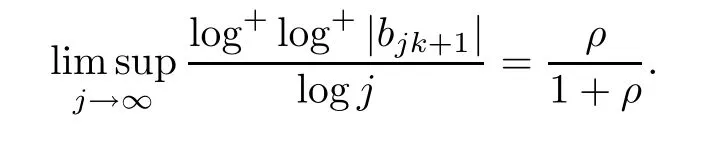
A
(z,ω
)is 1 a.s..The convergent radius ofA
(z,ω
)(t
=2,...,k
)is no less than 1 a.s..Then we can de fine the thek
-valued random analytic algebroid functionW
(z,ω
)in unit disc as follows: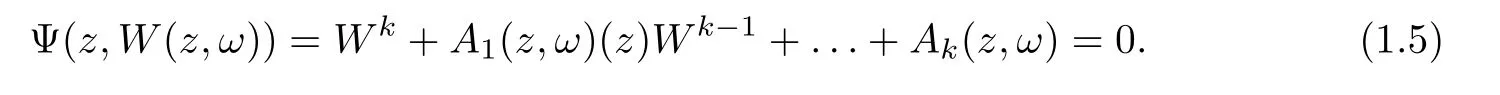
e
|u
∈[0,
2π
)}are the Borel points of orderρ
+1 ofA
(z,ω
),with no finite exceptional values a.s..In this paper,we will prove three theorems.First,we give two theorems on algebroid functions in the unit disc.The main idea of the proofs is from[2,10],in which the properties are proved when algebroid functions are de fined in the whole complex plane,and the proofs of these two theorems are similar to those in the whole complex plane.We give here complete proofs for the convenience of readers and the completeness of this paper.
Theorem 1.5
LetW
(z
)be ak
-valued algebroid function de fined by(1.1)in the disc{|z
|<R
}.Forb
∈C,Ψ(z,b
)/≡0,we have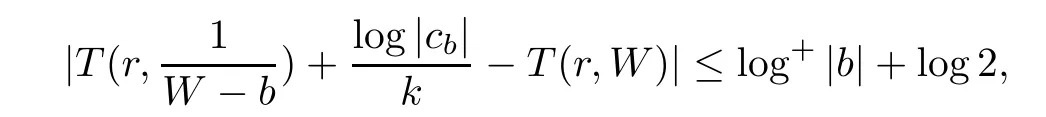
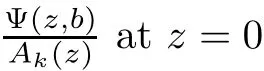
Theorem 1.6
For ak
-valued analytic algebroid functionW
(z
)of orderρ
(W
)de fined by(1.2)in unit disc,the equation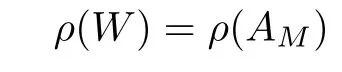
ρ
(A
)=max{ρ
(A
);t
=1,
2,...,k
}.
Now,we give the main theorem of this paper.
Theorem 1.7
LetW
(z,ω
)be ak
-valued random analytic algebroid function de fined by(1.5)in the unit disc.For almost surely allω
∈?,all points on the circle{e
;t
∈[0,
2π
)}are Borel points of orderρ
+1.2 Proof of Theorem 1.5
To prove Theorem 1.5,we need the following lemmas:
Lemma 2.1
Suppose thatf
(z
),g
(z
)are meromorphic functions in{|z
|<R
},wheref,g
/≡0 andf,g
/≡∞.Then for allr
∈(0,R
),we have
Proof
Forb
∈C,a
∈C,letn
(z
=b,f
=a
)be the multiplicities off
(z
)=a
at the pointz
=b
.Suppose that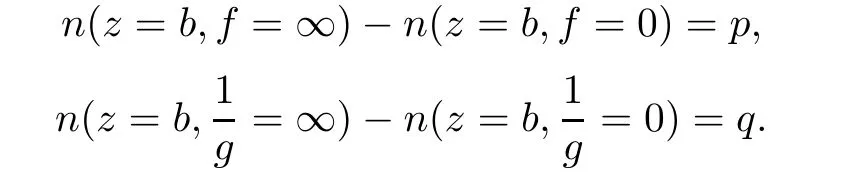
b
,we have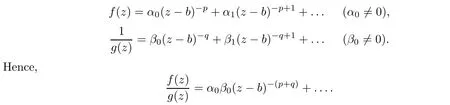
p
+q
≥0,we have
p
+q<
0,we have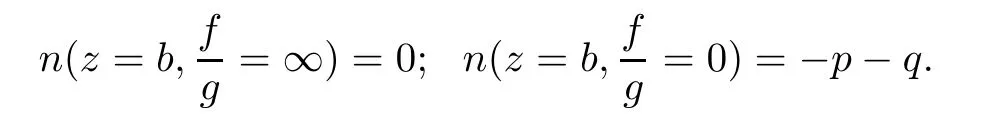
Therefore,
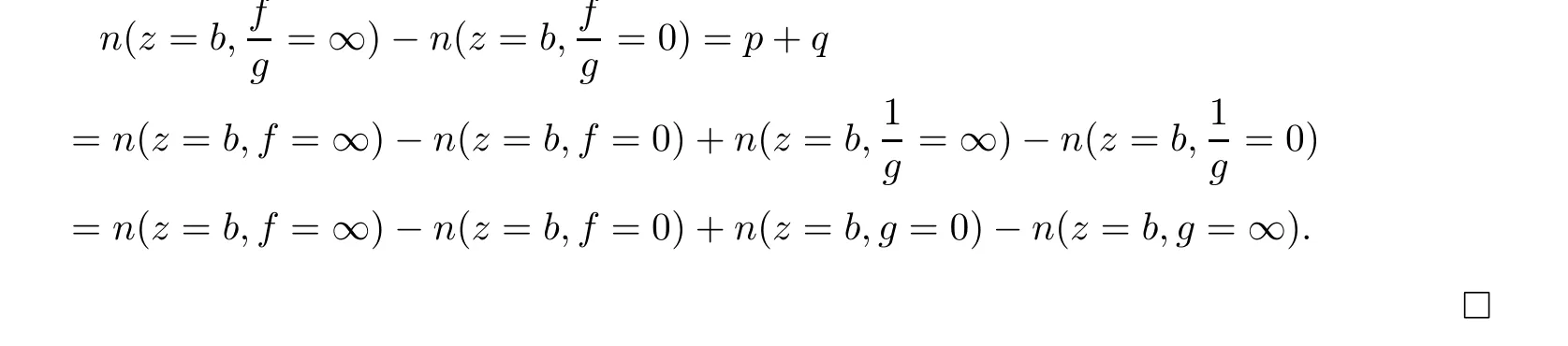
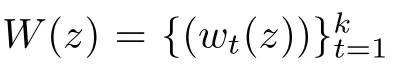
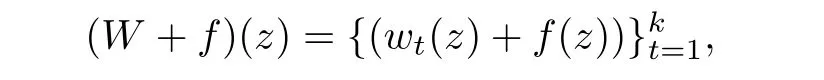
W
+f
)(z
)byW
(z
)+f
(z
).It is easy to see that the function(W
+f
)(z
)=W
(z
)+f
(z
)is ak
-valued algebroid function in{|z
|<R
}.The de finitional equation ofW
(z
)+f
(z
)is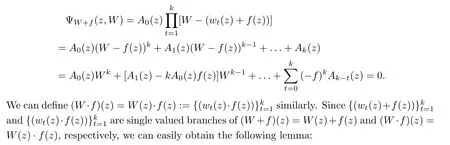
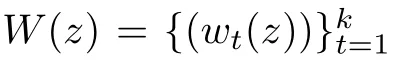
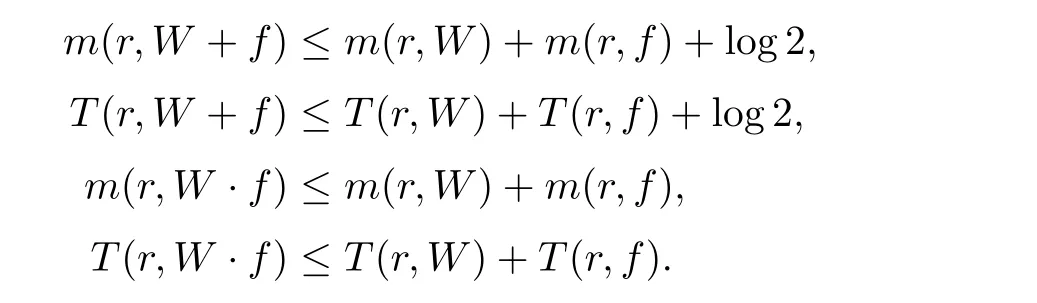
Lemma 2.3
(Jensen Formula of algebroid function)Suppose thatW
(z
)is ak
-valued analytic algebroid function de fined by(1.1)in{|z
|<R
}.Then,1.IfA
(z
)=Ψ(z,
0)/≡0,then
a
is the first non-zero coefficient in the Laurent expansion of the meromorphic function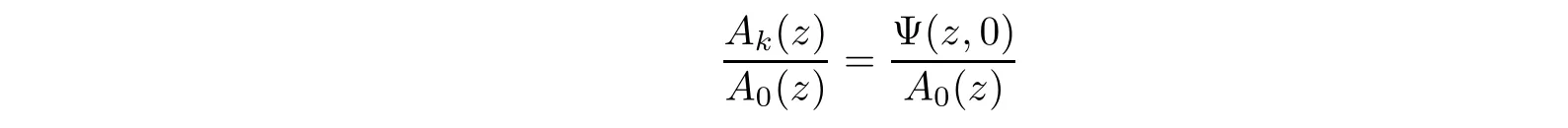
z
=0.2.More generally,if Ψ(z,b
)/≡0,then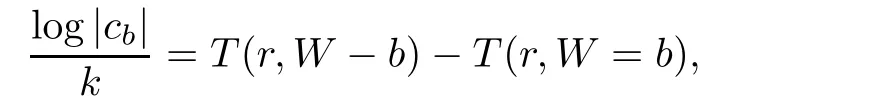
c
is the first non-zero coefficient in the Laurent expansion of the meromorphic function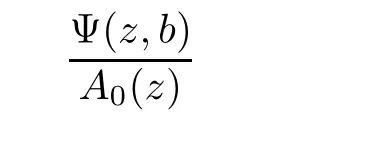
z
=b
.Proof
By a curve that goes through all branch points,|z
|<R
can be divided into a simply connected domainD
.Let{w
(z
)}bek
single branches ofW
(z
)inD
.i)By the Viete theorem,we have
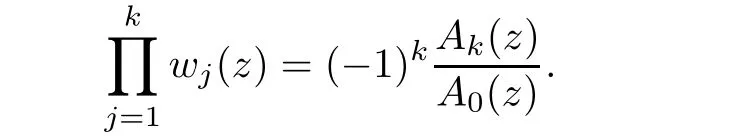
Using the Jensen Formula of meromorphic functions and Lemma 2.1,we get
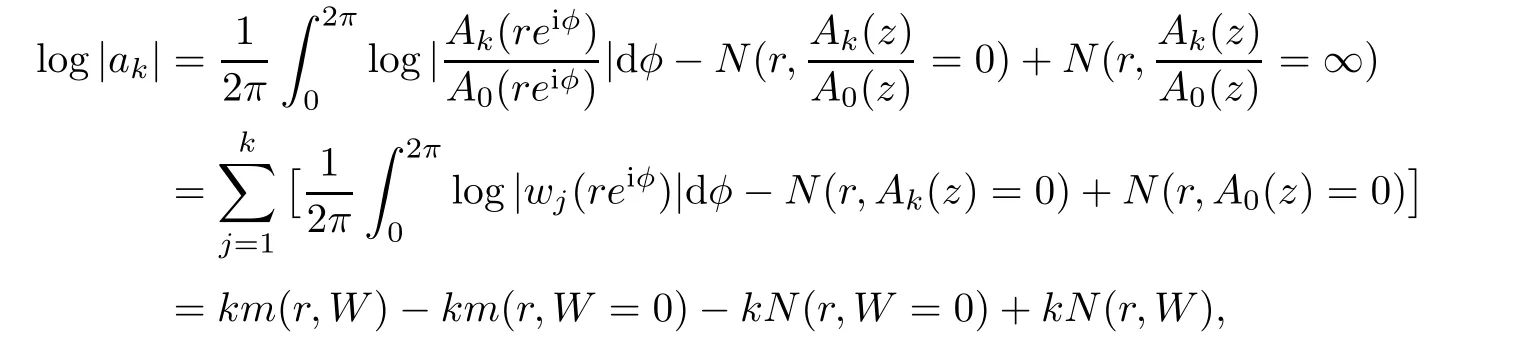
N
(r,A
(z
)=∞)=0=N
(r,A
(z
)=∞).ii)LettingM
=W
?b
,the equation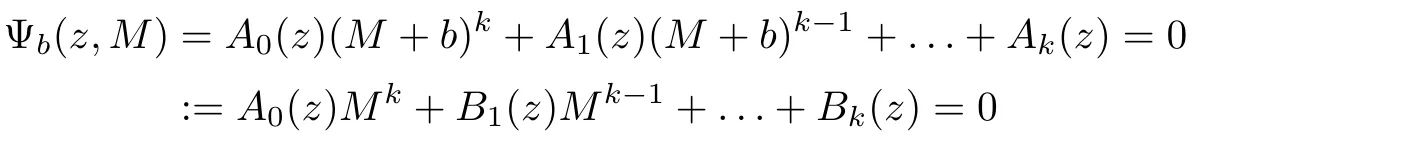
M
(z
).By conclusion(1),and by noticing the fact that Ψ(z,
0)≡Ψ(z,b
)≡B
(z
),we can obtain conclusion(2).Proof of Theorem 1.5
It follows from Lemma 2.2 that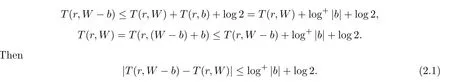
Applying the Jensen Formula of algebroid functions in Lemma 2.3,we have
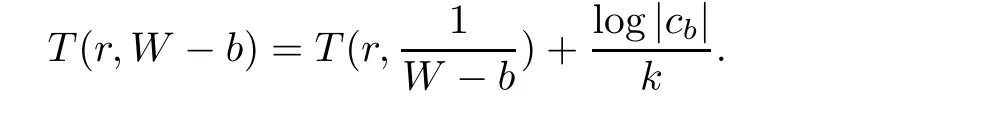
Combining with(2.1),we can obtain Theorem 1.5.
3 Proof of Theorem 1.6
To prove Theorem 1.6,we need several lemmas.
Lemma 3.1
([4])Suppose thatW
(z
)is ak
-valued algebroid function in{|z
|<R
}.Then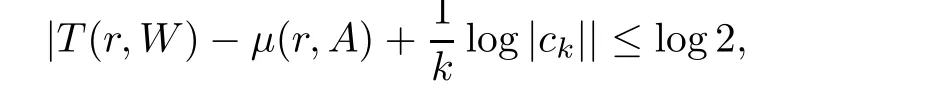
c
is the first non-zero coefficient in the Laurent expansion ofA
(z
)atz
=0 andμ
(r,A
)is de fined in De finition 1.4.Lemma 3.2
For an algebroid functionW
(z
)of orderρ
(W
)de fined by(1.1)in the unit disc,we have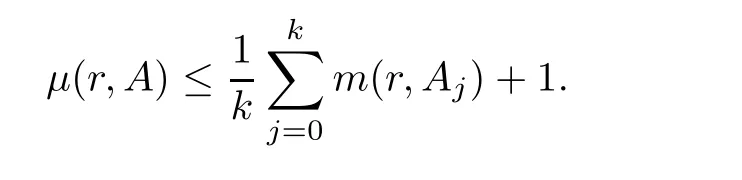
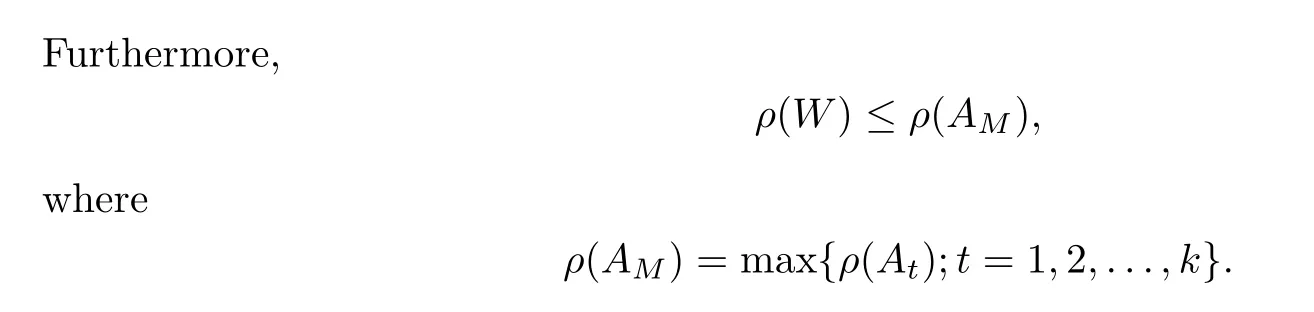
Proof
By De finition 1.4,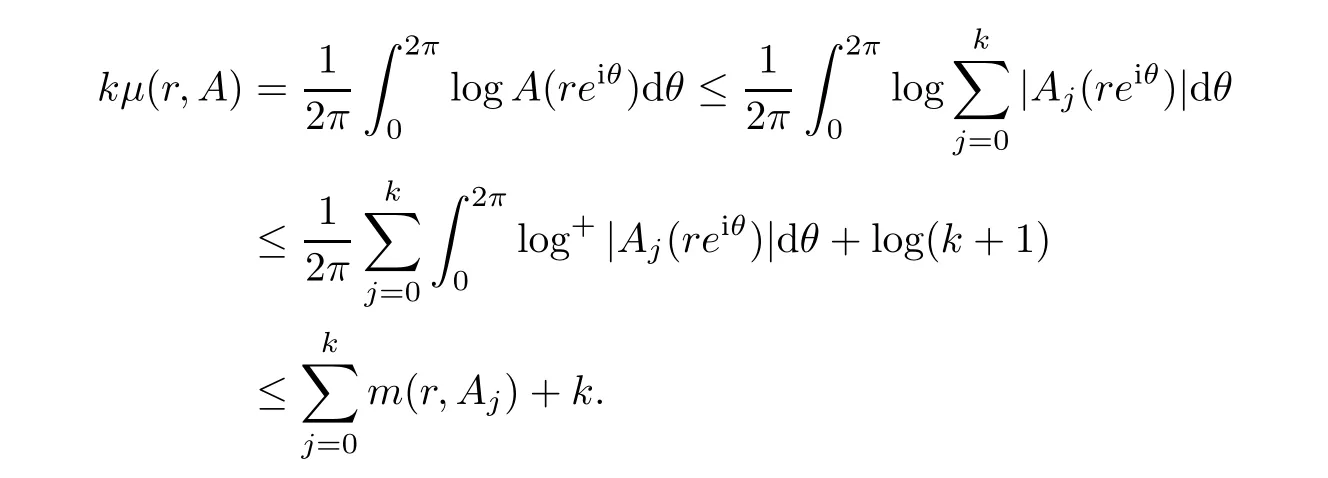
Hence,we can obtain
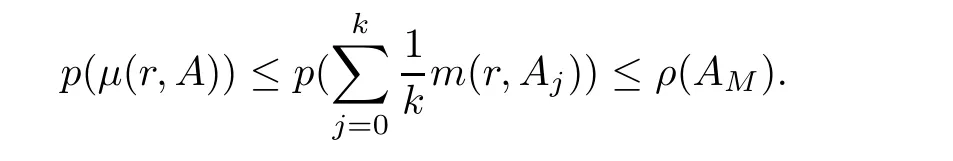
Applying Lemma 3.1,we have
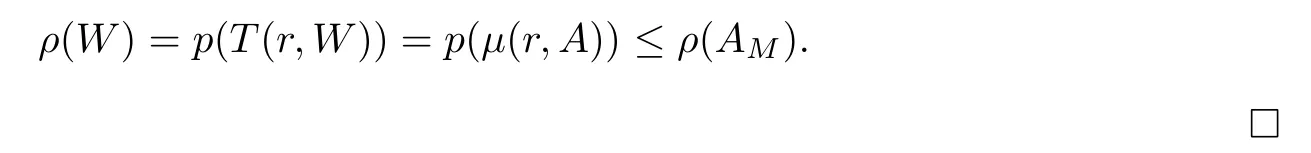
Remark 3.3
The equal sign in Lemma 3.2 may not hold.For example,let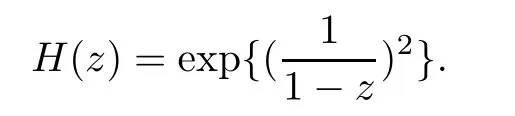
The 2-valued function
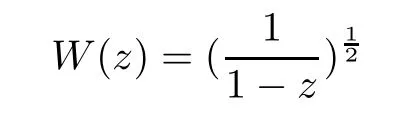
is de fined by the equation
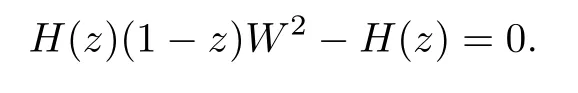
ρ
(W
)=0.However,ρ
(A
)=ρ
(A
)=ρ
(H
)=1.
Lemma 3.4
Suppose thatW
(z
)is an analytic algebroid function of orderρ
(W
)de fined by(1.2).Fort,u
∈{0,
1,
2,...,k
},we have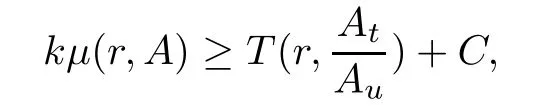
A
(z
)/≡0 andC
is a constant.In particular,if there existt,u
∈{0,
1,
2,...,k
}satisfying
Proof
Suppose thatA
(z
)/≡0.Let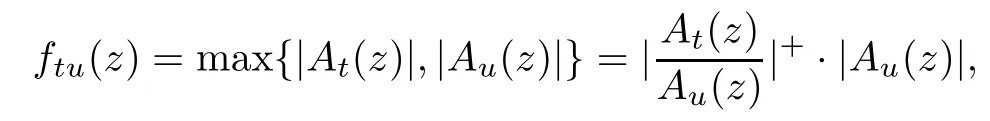
x
|=max{1,x
}.Then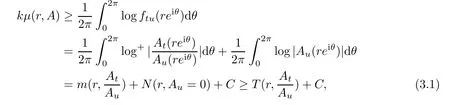
C
is a constant.If there existt,u
∈{0,
1,
2,...,k
}satisfying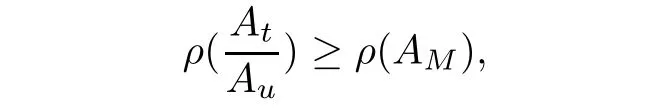
then according to Lemma 3.1 and(3.1),we can obtain
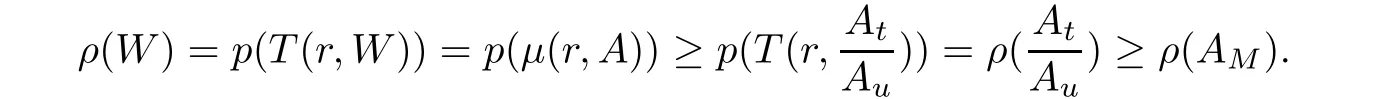
By applying Lemma 3.2,we have

Proof of Theorem 1.6
Noticing that theA
(z
)in expression(1.2)is equal to 1,we have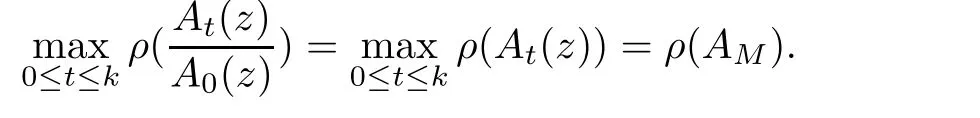
Therefore,we can easily obtain Theorem 1.6 from Lemma 3.4.
4 Proof of Theorem 1.7
To prove Theorem 1.7,we need a conformal mapping as follows:
Lemma 4.1
For all?>
0,mapping
z
;0<
|z
|<
1}∩{z
;|argz
|<?
}to the unit disc{|w
|<
1}.There is a constantb
∈(0,
1)depending on?
,such that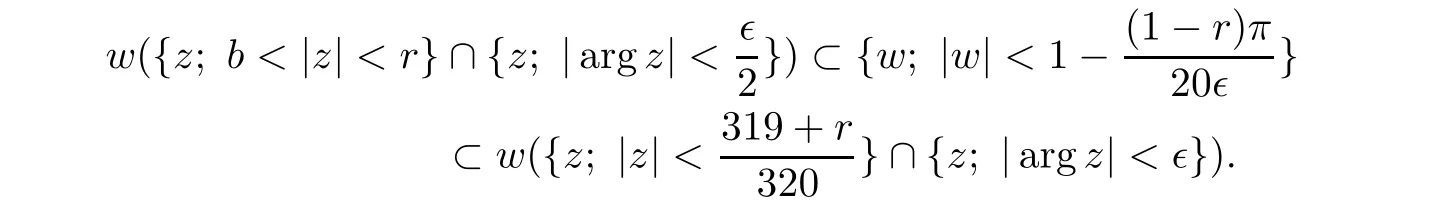
Proof
It follows from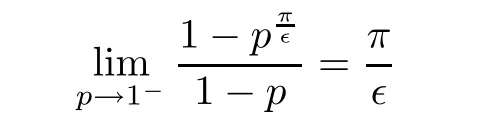
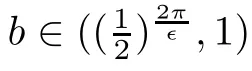
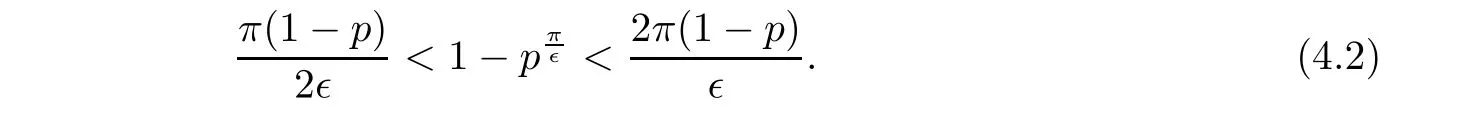
z
=pe
=p
cosφ
+ip
sinφ
,wherep
∈(b,
1)and|φ
|≤?
.Let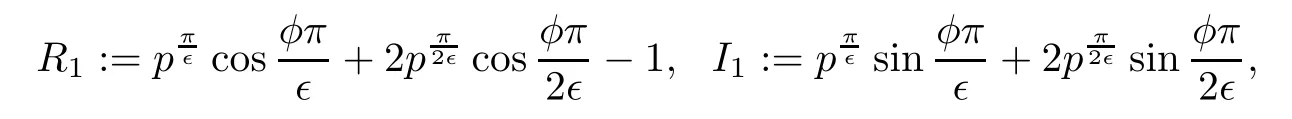
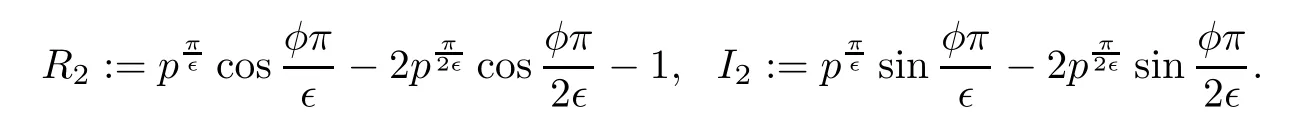
By(4.1),we have
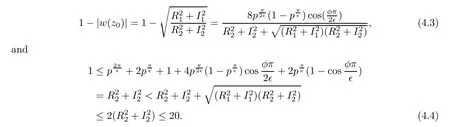
It follows from(4.2),(4.3)and(4.4)that

Lemma 4.2
Suppose thatn
(r
)is a positive real valued function in(0,
1).If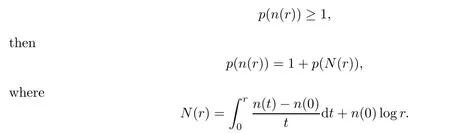
Proof
This Lemma has been proved in[11].For the convenience of the reader,we give here a brief proof.Suppose thatp
(n
(r
))=p
≥1,so for any?>
0,we have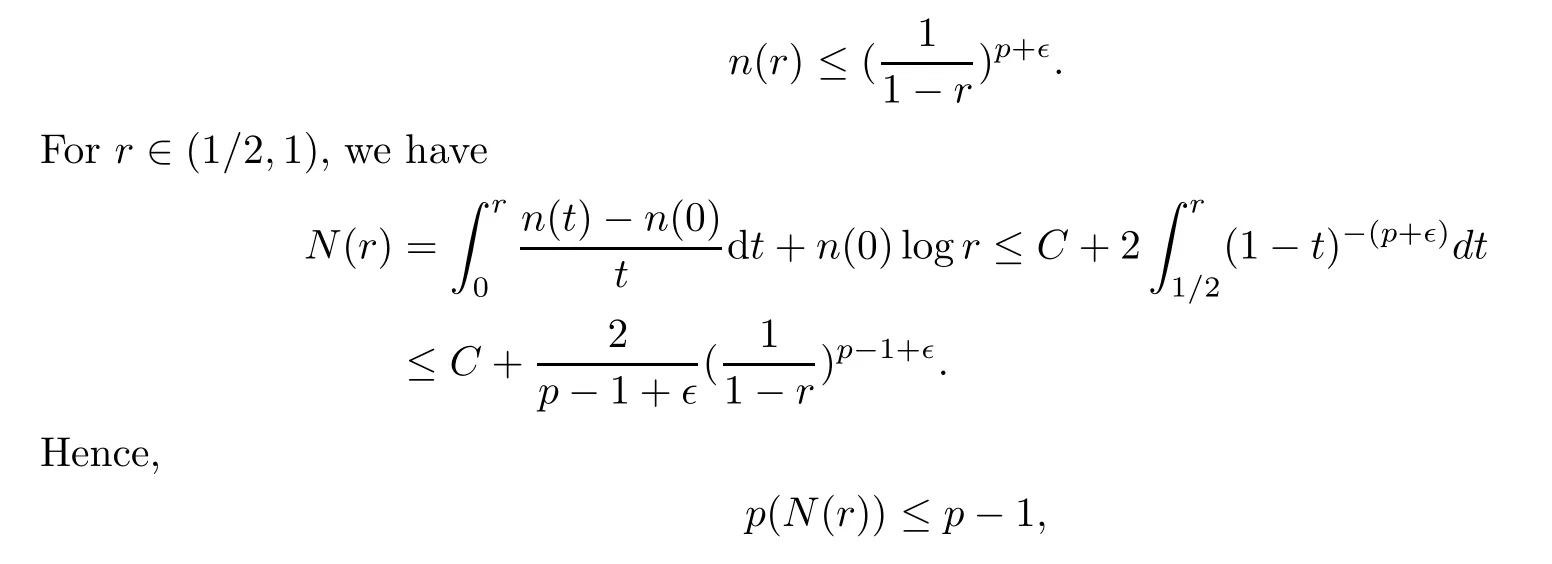
C>
0 is a sufficiently large constant.Since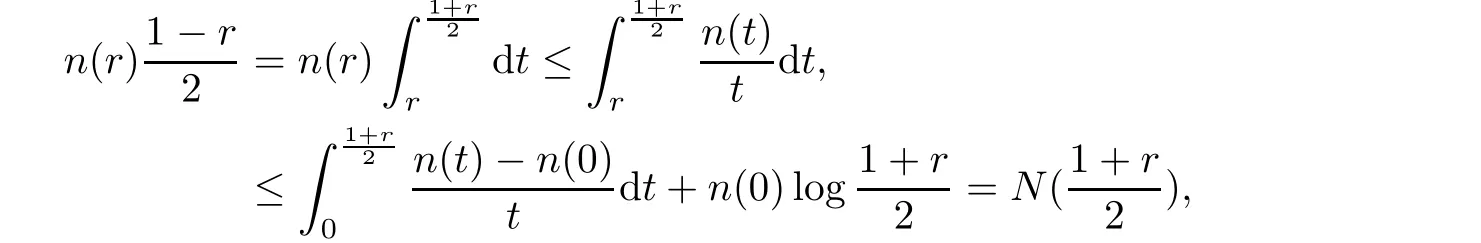
p
(n
(r
))≤p
(N
(r
))+1.
Proof of Theorem 1.7
According to[8],we know that all points on circle{e
;t
∈[0,
2π
)}are the Borel points of orderρ
+1 ofA
(z,ω
),with no finite exceptional values a.s.,that is,for allω
∈??E
,t
∈[0,
2π
),a
∈C
,δ
∈(0,π
),whereP
(E
)=0,we have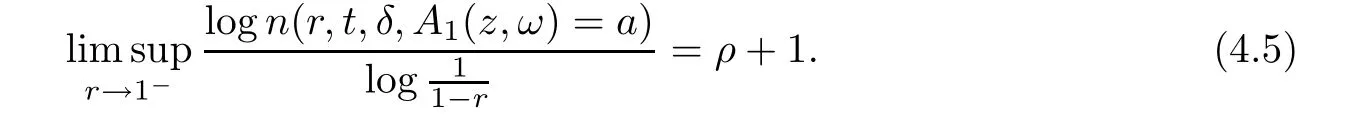
D
:={|z
|<
1}∩{|argz
|<?
}to unit discB
:={|w
|<
1}.Its inverse mapping is denoted byz
(w
).By Lemma 3.4,we have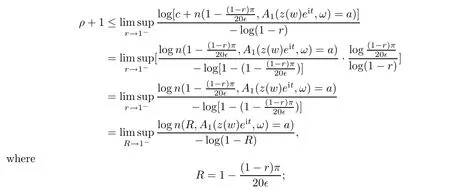
n
(r,A
(z
(w
)e
,ω
)=b
)is no less thanρ
+1.Hence,we know from Lemma 4.2 that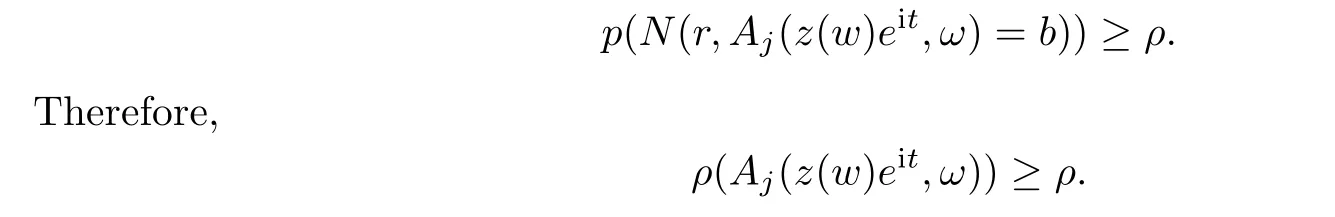
By Theorem 1.6,we have
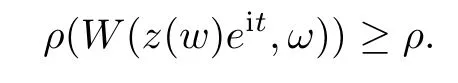
W
(z
(w
)e
,ω
),sayd
∈C,we have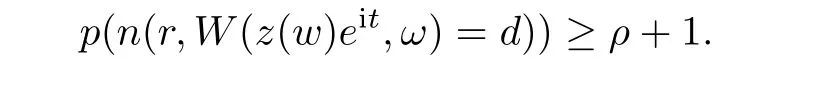
Applying Lemma 3.2,we have
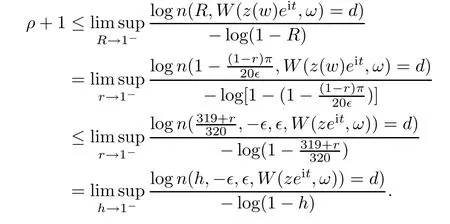
Then we have
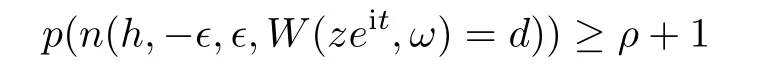
d
,ande
is the Borel point ofW
(z,ω
)of order more thanρ
+1.Since
e
is a Borel point of orderρ
+1. Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
