THE FIELD ALGEBRA IN HOPF SPIN MODELS DETERMINED BY A HOPF ?-SUBALGEBRA AND ITS SYMMETRIC STRUCTURE?
(魏曉敏) (蔣立寧)
School of Mathematics and Statistics,Beijing Institute of Technology,Beijing 100081,China
E-mail:wxiaomin1509@163.com;jianglining@bit.edu.cn
Qiaoling XIN(辛巧玲)
School of Mathematical Sciences,Tianjin Normal University,Tianjin 300387,China
E-mail:xinqiaoling0923@163.com
Abstract Denote a finite dimensional Hopf C?-algebra by H,and a Hopf?-subalgebra of H by H1.In this paper,we study the construction of the field algebra in Hopf spin models determined by H1 together with its symmetry.More precisely,we consider the quantum double D(H,H1)as the bicrossed product of the opposite dual of H and H1 with respect to the coadjoint representation,the latter acting on the former and vice versa,and under the non-trivial commutation relations between H1 and we define the observable algebra Then using a comodule action of D(H,H1)on we obtain the field algebra which is the crossed product and show that the observable algebra is exactly a D(H,H1)-invariant subalgebra of Furthermore,we prove that there exists a duality between D(H,H1)and implemented by a?-homomorphism of D(H,H1).
Key words Comodule algebra;field algebra;observable algebra;commutant;duality
1 Introduction
A system is made up of a large number of composite subsystems called“atoms”,which can be in a certain small number of microstates.Each state σ of the system,given by a microstate assigned to every atom,possesses a certain energy E(σ).A mathematical description of the system and the energy function E(σ)is called a model([1]).Quantum chains considered as models of 1+1-dimensional quantum field theory exhibit many features,including braid group statistics and quantum symmetry.These interesting features can be discussed in terms of Hopf spin models as a general class of quantum chains and can be described by Drinfeld’s quantum double D(H)of the underlying Hopf algebra H.
The most famous and fundamental of all models is the G-spin model,where G is a finite group.The G-spin models consist of atoms placed on the vertices and edges of a one-dimensional lattice,which can provide the simplest example of lattice field theory and exhibits quantum symmetry:
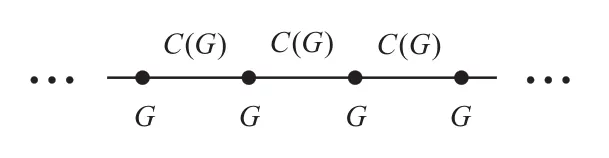
Generally,G-spin models with abelian group G have a symmetry group G×^G,where^G denotes the Pontryagin dual of G(the group of characters of G).If G is non-abelian,the Pontryagin dual of G is meaningless.Szlachányi and Vecsernyés in[2]generalized G×^G to D(G),which is defined as the crossed product of algebra C(G)of complex functions on G and algebra CG,and can be interpreted as the order-disorder type of quantum symmetry of G-spin models.On the foundations of commutation relations of order-disorder operators,Szlachányi and Vecsernyés defined the field algebra F in G-spin models,and furthermore,established the observable algebra A as a D(G)-invariant subalgebra.However,as the disorder part of the double D(G),the algebra C(G)is always abelian,so G-spin models cannot be selfdual in the Kramers-Wannier sense([3]),unless the group G is abelian.Non-abelian Kramers-Wannier duality therefore needs to be considered in a larger class of models.It makes sense to further generalize the G-spin models in terms of the general models.In 1997,Nill and Szlachányi([4])studied the Hopf spin models as the generalization of G-spin models,since the finite group algebra CG is a Hopf C?-algebra of finite dimension.In Hopf spin models,there is a copy of finite dimensional Hopf C?-algebra H on each lattice site,and a copy of its dualon the link;non-trivial commutation relations are postulated only between neighboring links and sites,so the observable algebra A can be constructed by generators H and.Subsequently,the corresponding field algebra F is obtained under the coaction of D(H)on A.At the same time,V.Schomerus discussed the construction of field algebras with quantum symmetry from local algebras([5]).Specifically,it was shown that field algebras can be constructed by some field operators which are obtained by acting on a positive definite Hilbert space of states and transform covariantly under the quantum symmetry,and that they obey local braid relations.
The article[6]defines the field algebra FNdetermined by a normal subgroup N in G-spin models,where G is a finite group,and gives the observable algebra ANas the D(N,G)-invariant subalgebra of FN.Furthermore,the symmetric structure of FNis fulfilled by the double D(N,G),which is the crossed product of the algebra C(N)and group algebra CG.Motivated by all of the above,this paper considers a more general situation in Hopf spin models,which can be shown in the following one-dimensional lattice model:let H be a Hopf C?-algebra of finite dimension over a complex field,H1be a Hopf?-subalgebra of H,with the model consisting of copies of H1on lattice sites andon links together with non-trivial commutation relations between H1and,such that

Then one can construct a C?-subalgebra AH1of the observable algebra A in Hopf spin models by generators H1and;this is called the observable algebra in Hopf spin models determined by H1.

2 Preliminaries
Definition 2.1([7]) Let(H,m,ι,Δ,ε,S)be a Hopf algebra over the complex field C.We say that H is a Hopf?-algebra if there exists an antilinear involution?on H satisfying the following two conditions:
(1)the map?is an antimorphism of real algebras,as well as a morphism of real coalgebras.In other words,for every a∈H,
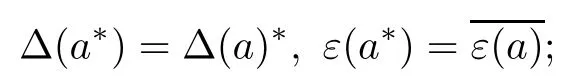
(2)the map?is compatible with the antipode S of H,
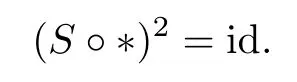
Definition 2.2([8]) Suppose that(H,Δ)is a pair of finite dimensional C?-algebra with a unital?-homomorphism Δ:H→H?H.We call this pair a Hopf C?-algebra if the following conditions hold:
(1)(Δ?id)°Δ=(id?Δ)°Δ;
(2)the linear spaces span{Δ(H)(H?1)}and span{Δ(H)(1?H)}both are equal to H?H.
Such a Δ is called the comultiplication of H.(H,Δ)is said to be cocommutative if τ°Δ=Δ,where τ:H?H→H?H is a flip,τ(a?b)=b?a,a,b∈H.
There exist linear maps
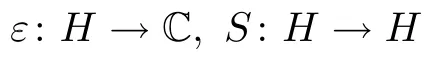
satisfying the following properties:
(1)ε is a unital?-homomorphism,and S is a unital?-preserving anti-multiplicative involution;
(2)(ε?id)°Δ=(id?ε)°Δ=id;
(3)m°(S?id)°Δ=m°(id?S)°Δ=ι°ε,where m,ι are the multiplication and unit,respectively.
We say that ε is a counit,and S is an antipode of(H,Δ).In this case,(H,Δ,ε,S,?)is a Hopf C?-algebra of finite dimension.
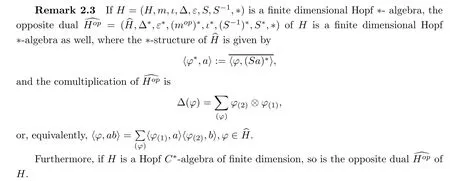
Example 2.4Let H be a finite dimensional Hopf C?-algebra.Then Drinfeld’s quantum double D(H)([7])is also a Hopf C?-algebra.
Definition 2.5Let H be a Hopf?-algebra,and A be a?-algebra.A bilinear map γ:H?A→A is an action of H on A if the following hold for any a,b∈A,x,y∈H:
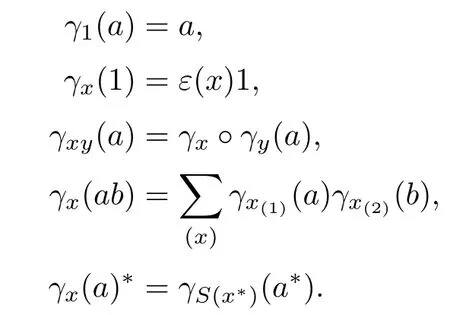
In this case,A is called a left H-module algebra.
Remark 2.6The map γ is assumed to be weakly continuous with respect to A and continuous with respect to some C?-norm on H(which is unique in the case of finite dimensionality).In the case of Hopf C?-algebra,γ is assumed to be continuously related to the C?-norm on H.
Definition 2.7Let H be a Hopf algebra,and A be a coalgebra.If A is a left H-module with respect to the linear map γ:H?A→A,and the comultiplication and counit structure maps of A are H-module morphisms,namely,for any a,b∈A,x,y∈H,

then A is said to be a left H-module coalgebra.
For more detail about Hopf algebras one can refer to[9–12],and some definitions and properties about Hopf C?-algebras can be found in[13–17],etc..We now present Sweedler’s sigma notation,which is standard in Hopf algebra theory.Denote the comultiplication,the counit and the antipode of Hopf algebra H by Δ,ε and S,respectively.If c is an element of H,the element Δ(c)of H?H is of the form

Moreover,if the coassociative law

holds,then

The counitary and antipode properties can be expressed by Sweedler’s notation as well.
3 The Field Algebra Determined by D(H,H1)
From now on,let(H,m,ι,Δ,ε,S,?)be a finite dimensional Hopf C?-algebra,and let H1be a Hopf?-subalgebra of H.Then H and H1are semisimple and involutive with S2=id([16]).We still denote the structure maps of H1by Δ,ε,S,and denote the dual of H1bywhich is also a Hopf C?-algebra.
3.1 The quantum double D(H,H1)
As shown in[18,19],the construction of Drinfeld’s double is investigated for any regular multiplier Hopf?-algebra pairings,which generalizes the quantum double construction of ordinary Hopf algebra pairings.In these papers,two dually paired regular multiplier Hopf?-algebras A and B,associated with a bilinear mapping〈·,·〉:A×B→C and satisfying certain properties,can yield a quantum double which is again a regular multiplier Hopf?-algebra.Delvaux and Van Daele in[19]constructed Drinfeld’s double related to the pairing〈A,B〉by using appropriate representations of A and B on the vector space B?A.If A and B are Hopf algebras,then the quantum double multiplier Hopf algebra is the usual quantum double.In particular,the finite dimensional Hopf?-algebrasand H1form a regular multiplier Hopf?-algebra pairing which allows us to construct the quantum double D(H,H1)by using appropriate representations.
Now we review the definition of the quantum double D(H,H1).
We will have one between us, continued the old dame; and as you are the visitor, you shall have the half which contains the stone; but be very careful that you don t swallow it, for I keep them against the winter, and you have no idea what a good fire they make
Lemma 3.1Let H be a finite dimensional Hopf?-algebra,and let H1be a Hopf?-subalgebra of H.Let α:be the coadjoint representations given by
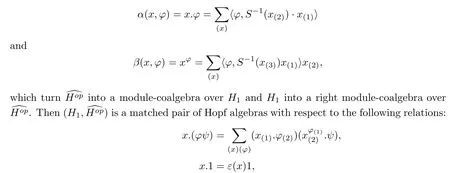


in terms of(S°?)2=id for ?∈and x∈H1.Combining these results,D(H,H1)is a Hopf?-algebra. □
A left invariant Haar functional on the Hopf algebra H is a non-zero linear map ?:H→C satisfying the property(id??)Δ(a)=?(a)1 for all a∈H.Similarly,a right invariant Haar functional is a linear map ψ:H→C with the property(ψ?id)Δ(a)=ψ(a)1.When the left and the right invariant Haar functionals coincide,we called it the Haar functional,or the Haar measure.If H is a Hopf C?-algebra of finite dimension,there exists a normalized Haar measure on H so that H is involutive([16]).Denoting λ,Λ as the normalized Haar measures onand H1,respectively,we then get that for ??x∈D(H,H1),

defines a faithful positive linear functional on D(H,H1).According to the GNS construction([20]),the map〈·,·〉:D(H,H1)→C given by〈??x,ψ?y〉=θ((ψ?y)?(??x))is an inner product on D(H,H1)such that D(H,H1)is a Hilbert space.For each ??x∈D(H,H1),
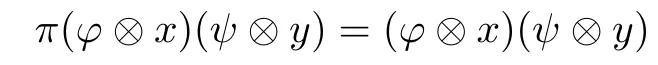
is a faithful?-representation on D(H,H1),so D(H,H1)is a C?-algebra of finite dimension with C?-norm([21])
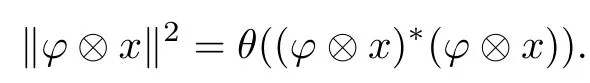
Therefore the quantum double D(H,H1)is a Hopf C?-algebra of finite dimension.
3.2 The field algebra in Hopf spin models determined by a Hopf?-subalgebra
With the assumptions and notations as above,H is a finite dimensional Hopf C?-algebra,and H1is a Hopf?-subalgebra of H.We denote the elements of D(H,H1)by ?x instead of ??x=just to make the subsequent computation clearer.Thus D(H,H1)can be denoted as a?-algebra generated by H1andtogether with the following cross relation,which is in accord with the relation(3.1):
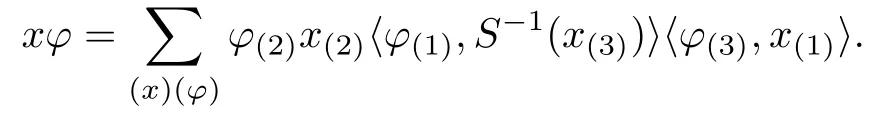
Here x∈H1,?∈,and(x?)?=??x?.The structure maps Δ,ε and S are still adopted as relations(3.2)?(3.4).
The dual Hopf?-algebra of the D(H,H1)is determined by the following structure maps(we still denote them by Δ,ε,S):

Remark 3.5By the antipode of H1,together with the relation S2=id,the commutation relations above are equivalent to the following relations:

Our method for constructing the field algebra determined by H1will be to give the coaction of D(H,H1)on the local observable algebraof the finite interval.Here we review some conceptions of right comodule algebra.
Definition 3.7([9]) Let(H,m,ι,Δ,ε)be a bialgebra.If an algebra A is also a right H-comodule with respect to the map γ:A→A?H,that is,
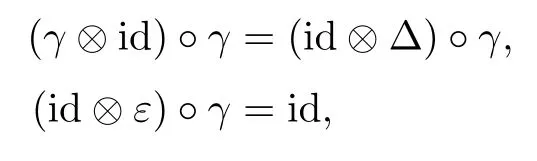
and the structure maps,multiplication and unit of A are right H-comodule morphisms,namely,when

then A is said to be a right H-comodule algebra.
Actually,A is a right H-comodule algebra if and only if A has an H-comodule structure given by a map γ:A→A?H,and the map γ is a morphism of algebras.
Then the coaction of D(H,H1)onis given by the follows:
Proposition 3.8For i∈Z,the linear maps ρ2i,2i+1:A2i,2i+1→A2i,2i+1?D(H,H1)with respect to the natural comultiplicationwhich are given by

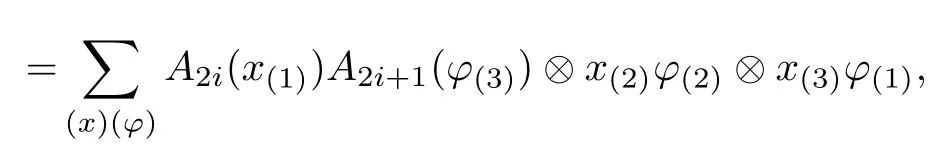
and
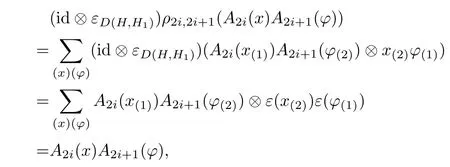
which forms the desired result.

and the penultimate equation follows from the relation S2=id in D(H,H1).Hence the local observable algebra of finite interval A2i,2i+1is a right D(H,H1)-comodule algebra. □
Remark 3.9We have an equivalent definition of ρ2i,2i+1as follows:
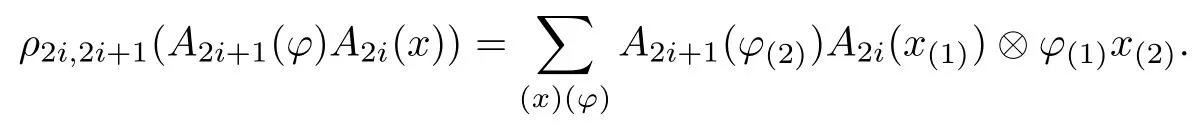
Similarly,there is a right(D(H,H1),Δop)-comodule algebrastructure on the algebra A2i?1,2i,i∈Z given by
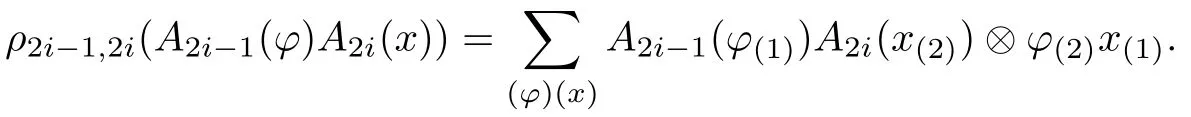
Now we construct the coaction of D(H,H1)on the local observable algebra of finite interval A2i,2i+2n+1(n∈N).According to iterated application of the Takesaki duality theorem,we have the?-algebra inclusion
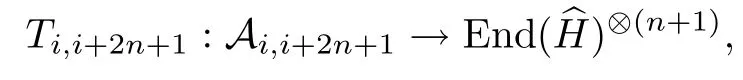
where Ti,i+1is given by

Next,we put
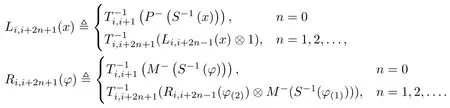
Then Li,i+2n+1and Ri,i+2n+1define?-algebra inclusions.
Therefore,when n≥1,we can define ρ2i,2i+2n+1:A2i,2i+2n+1→A2i,2i+2n+1?D(H,H1)by

obeys the following relation:

and ρε(A)=A,meaning that the comodule algebra structure of D(H,H1)on the algebra A2i,2i+1uniquely determines the module algebra structure on A2i,2i+1fulfilled by the map

Using the continuity and uniqueness of the C?-inductive limit,one can get

and,

Remark 3.12Sinceis a left D(H,H1)-module algebra,and D(H,H1)is a semisimple algebra([21]),the field algebrais completely reducible,and can be decomposed into a direct sum

Here we omit the proofs,since the above result can be obtained in the following way:for locally compact quantum groups in a von Neumann algebraic setting,the fixed point subalgebra of the crossed product N?M,associated to the the natural dual action ofon N?M,is given by the original algebra N([26]).Furthermore,in the algebraic framework,this property also holds for algebraic quantum groups without the assumption on the topological structure([27]).
In particular,we have
Corollary 3.14where Z∈D(H,H1)is a normalized integral.
4 The Duality Between the Observable Algebra and D(H,H1)
This section will consider the symmetric structure of field algebra in Hopf spin models determined by a Hopf?-subalgebra.


This is exactly
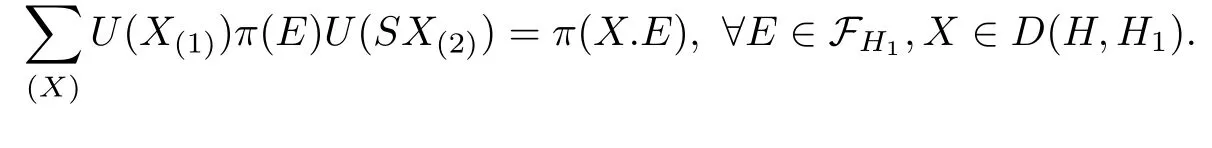
One can verify that

Now we come to the final result of this section,which gives a duality between the finite dimensional C?-algebra D(H,H1)and the observable algebraand thus exhibits the quantum symmetry in Hopf spin models determined by H1exactly.
Theorem 4.2With the assumptions and notations as above,
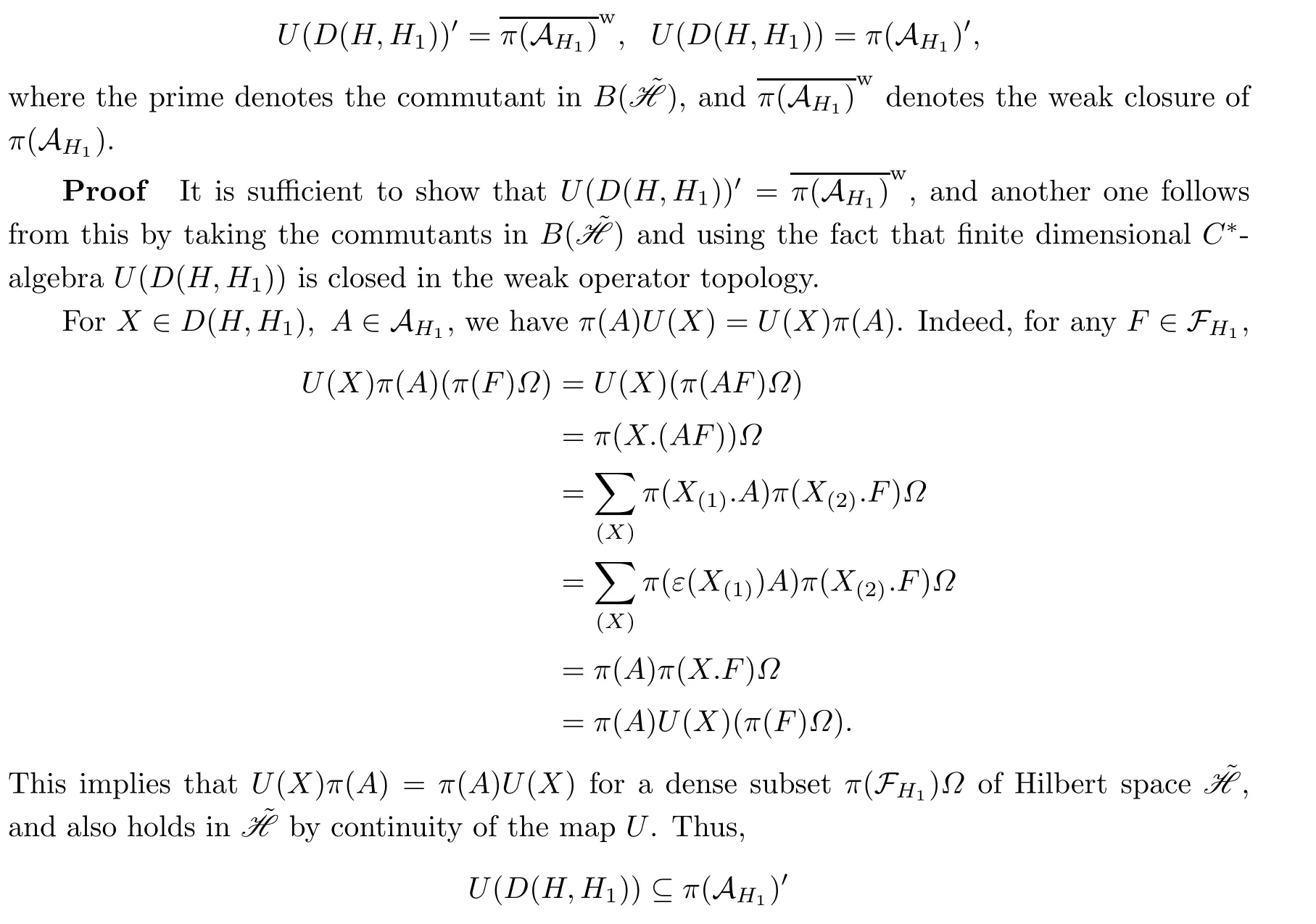
or

where the equality follows from the fact that U(D(H,H1))′is a von Neumann algebra,and is thus closed in the weak operator topology.

The last shows that
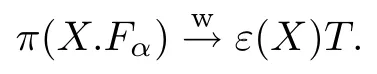
In particular,letting X=Z be the normalized integral of D(H,H1),one can get
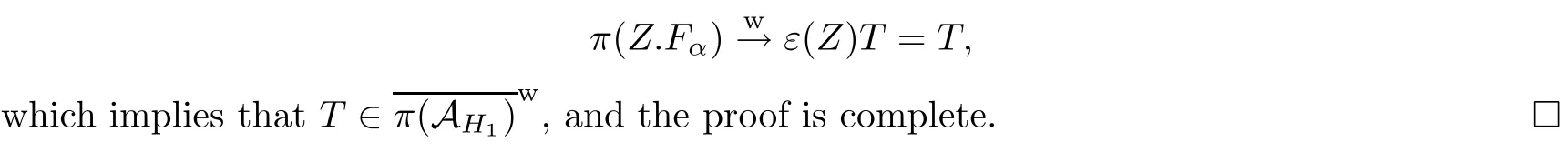
 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
- Acta Mathematica Scientia(English Series)的其它文章
- ANALYSIS OF THE GENOMIC DISTANCE BETWEEN BAT CORONAVIRUS RATG13 AND SARS-COV-2 REVEALS MULTIPLE ORIGINS OF COVID-19?
- DYNAMICS ANALYSIS OF A DELAYED HIV INFECTION MODEL WITH CTL IMMUNE RESPONSE AND ANTIBODY IMMUNE RESPONSE?
- BILINEAR SPECTRAL MULTIPLIERS ON HEISENBERG GROUPS?
- ON SCHWARZ-PICK TYPE INEQUALITY FOR MAPPINGS SATISFYING POISSON DIFFERENTIAL INEQUALITY?
- EXISTENCE AND UNIQUENESS OF THE GLOBAL L1 SOLUTION OF THE EULER EQUATIONS FOR CHAPLYGIN GAS?
- UNIQUENESS OF THE INVERSE TRANSMISSION SCATTERING WITH A CONDUCTIVE BOUNDARY CONDITION?
