An iterative construction of Riemann mappings*

DENG Fusheng, JIANG Weiwen, ZHANG Xujun

(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)

Abstract In this note, we give an explicit construction of iterative approximation of Riemann mappings. Our method is motivated by Koebe’s proof of the Riemann mapping theorem.

Keywords Riemann mapping; Montel’s Theorem; Hurwitz’s Lemma

For polygon areas, Riemann mappings have some special forms, known as the Schwarz-Christoffel formula[1]. In Ref.[2], Thurston gave a geometric approach to the construction of Riemann mappings. Thurston’s method was further developed in Ref.[3]. Based on Bishop’s methods[4], Cheng[5]studied explicit construction of Riemann mapping, by considering a condition called mappability.

In this note, we give a different explicit construction of iterative approximation of Riemann mappings. Our method is motivated by Koebe’s proof of the Riemann mapping theorem, as presented in Ahlfors’ classic Ref.[1]. The construction in the present note can be easily realized as a computer program, except the choices of the pointswk(see section 2 for details) which will be further studied in forthcoming works.

1 Proof of Riemann mapping theorem

In this section, we present a proof of the Riemann mapping theorem which is due to Koebe (see Ahlfors[1]). Inspired by the idea in this proof, we will give an explicit iterative construction of conformal mappings from simply connected domains onto the unit disc.

ProofThe proof is taken from Ref.[1]. The analytic property encoded by the simply connectedness that will be used in the proof is the existence of square root of any holomorphic function onDwithout zeros. The uniqueness part follows easily from Schwarz Lemma. We give a proof of the existence off, which is divided into several steps as follows.

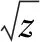
σ+(D)∩σ-(D)=?.

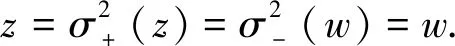
It is also clear thatσ+andσ-are injective, hence we haveσ+(D)?D.

Step 2. We consider the set:={g∈(D)|g:D→Δ is injective,g(z0)=0}.From Step 1 we know thatis not empty. Letλ=sup{|g′(z0)| |g∈}. From the Cauchy inequality we haveλ<+∞. Take a sequencegj∈, such thatBy Montel’s theorem, we may assume {gj} converge to a holomorphic functionf∈(D) on every compact subsetKofD. We have

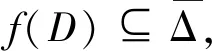
Step 3. The last step is to show thatfis surjective. We argue by contradiction. Iffis not subjective, there exists a pointw0∈Δf(D). Set

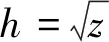
A straightforward calculation shows:

This leads to a contradiction by the definition ofλ.

After a gyration, we havef′(z0)>0.

□

The mapping in the above theorem is called a Riemann mapping.

2 Iterative construction of Riemann mapping

Step 1. We imbedDinto the unit disk Δ by complex affine mapping. There existsr>0 such thatf1(z)=r(z-a) mapsDinto Δ withf1(z)=0 andf′1(a)>0. IfDis a disc, then we get our results becausefis clearly surjective for suitabler; ifDis not a disc, we continue our construction.

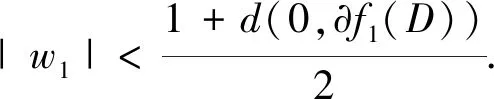
f2(z)=α1ψh(-w1)°h°ψw1°f1(z),

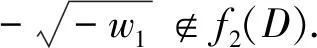
fj+1(z)=αjψh(-wj)°h°ψwj°fj(z),

From the above steps we get a sequence of holomorphic injective mappings {fj:D→Δ} with

fj(a)=0,f′j(a)>0.

Theorem2.1Let {fj} be the sequence constructed above. Then {fj} converges to a biholomorhpic mappinggfromDto the unit disk Δ such thatg(a)=0 andg′(a)>0, uniformly on compact subsets ofD.

ProofBy the uniqueness of the Riemann mappingf:D→Δ withf(a)=0 andf′(a)>0, it suffices to show that any subsequence of {fj} has a subsequence that converges to the Riemann mappingfuniformly on compact sets of Δ.

By the Cauchy’s inequality, there existsb>0 such that |f′j(a)|≤b∈for allj. Note that

|wj|→1.

Recall that we have

thus we can obtain that

d(0,?fj(D))→1.