n個自然數(shù)立方和的簡單幾何證明
江西省高安市第二中學(xué)(330800) 湯永發(fā)
1 引言
在高中數(shù)學(xué)選修2-2(北師大版)教材的第一章”推理和證明”的內(nèi)容中,教材提供了n個自然數(shù)的平方和的證明過程,我們可以利用歸納和類比的方法來證明n個自然數(shù)的立方和的結(jié)論.本文將提供一種更簡單直觀的幾何證明法來論證n個自然數(shù)的平方和與立方和的結(jié)論.
2 n個自然數(shù)平方和的證明
命題1若n ∈N+,則
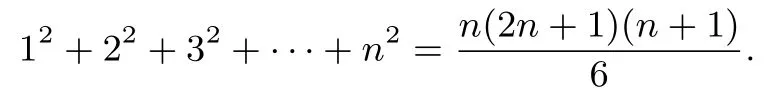
證明由于12+22+32+···+n2=1+(2+2)+(3+3+3)+···+n+n+n+···+n,不妨將上式的右邊寫成如下圖1所示的等邊三角形:

圖1
那么該等邊三角形中所有數(shù)之和為:
12+22+32+···+n2.將等邊三角形(圖1)繞其對稱中心逆時針旋轉(zhuǎn)60°,得圖2:
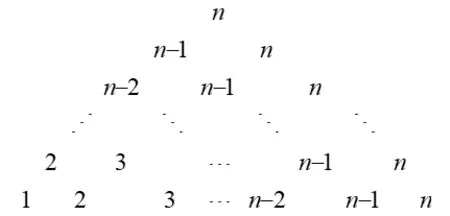
圖2
所得的等邊三角形(圖2)中的所有數(shù)字之和仍然是12+22+32+···+n2.再將等邊三角形(圖2)繼續(xù)繞其對稱中心逆時針旋轉(zhuǎn)60°,得下圖:
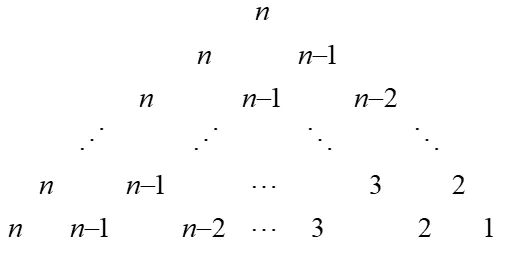
圖3
將所得到的等邊三角形圖1-3 在同一個位置對應(yīng)的三個數(shù)相加之后,得到新的等邊三角形(圖4),如下圖所示:
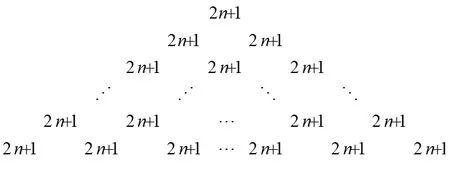
圖4
等邊三角形(圖4)共有1+2+3+···+n個數(shù),每個數(shù)都是2n+1.也就可以得到:
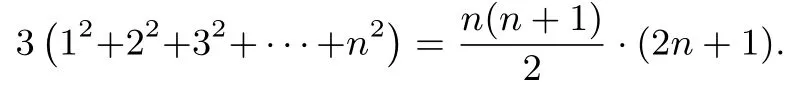
從而證明得到:
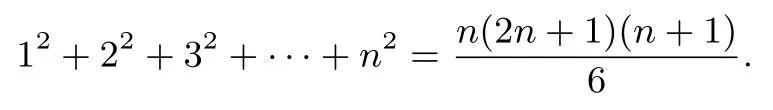
3 n個自然數(shù)立方和的證明
命題2若n ∈N+,則13+23+33+···+n3=
證明:由于k3=(k×k)×k.不妨將k3寫成如圖5所示的n排n行的正方形:
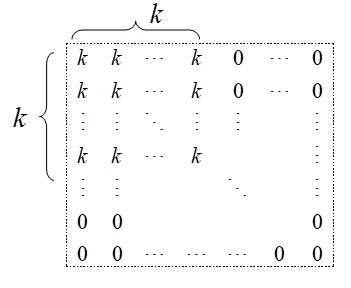
圖5
即正方形中n×n個數(shù)字之和等于k3.于是13+23+33+···+n3就可寫成:
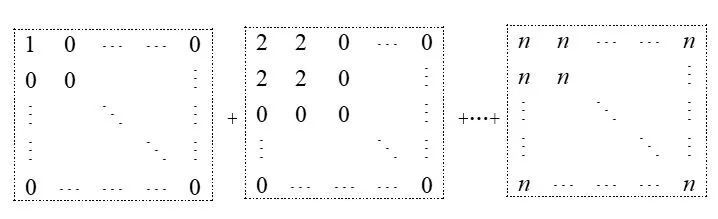
圖6
令Sk=1+2+···+k,Mk=k+(k+1)+···+n(k ∈N+,k ≤n).所以相加后圖6式化為:
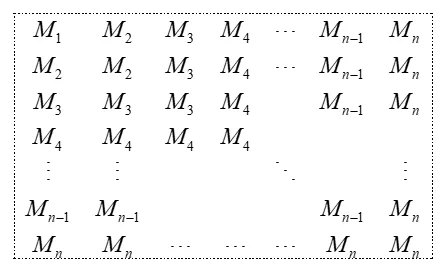
圖7
由圖7知,正方形對角線(M2,M3,M4,M5,...,Mn)的上下兩部分是相同.不妨考慮對角線上面部分的總和:M2+2×M3+3×M4+4×M5+···+(n-1)×Mn=2×S1+3×S2+4×S3+5×S4+···+n×Sn-1.
所以圖7可以寫成:
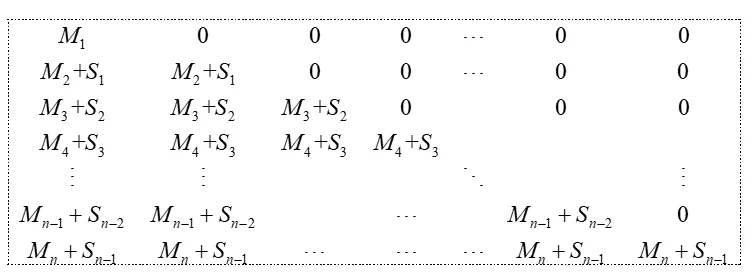
圖8
又因?yàn)镾n=Mk+Sk-1,(k ∈N+,2≤k ≤n)且Sn=M1.所以正方形圖8可化成:
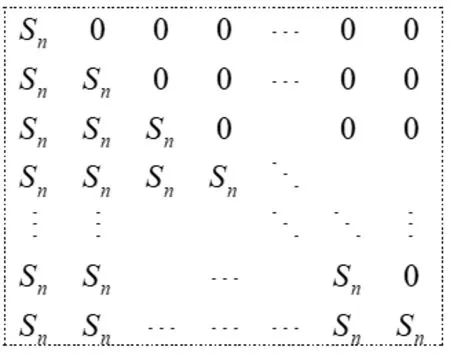
圖9
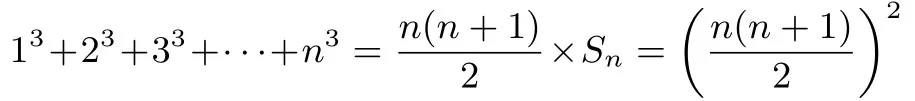
從而結(jié)論得證.
本文從另一個新穎的角度,聯(lián)系學(xué)生熟悉的等邊三角形與正方形,更加簡單明了,更加形象的給出了n個自然數(shù)平方和與立方和相關(guān)結(jié)論的證明.將一個數(shù)論問題巧妙的通過幾何的方式得到很有效的證明,從而很好體現(xiàn)了數(shù)學(xué)教學(xué)中幾何直觀想象的核心素養(yǎng)的重要性.

