Distributed Adaptive Cooperative Tracking of Uncertain Nonlinear Fractional-order Multi-agent Systems

Zhitao Li, Lixin Gao, Wenhai Chen, and Yu Xu

Abstract—In this paper, the leader-following tracking problem of fractional-order multi-agent systems is addressed. The dynamics of each agent may be heterogeneous and has unknown nonlinearities. By assumptions that the interaction topology is undirected and connected and the unknown nonlinear uncertain dynamics can be parameterized by a neural network,an adaptive learning law is proposed to deal with unknown nonlinear dynamics, based on which a kind of cooperative tracking protocols are constructed. The feedback gain matrix is obtained to solve an algebraic Riccati equation. To construct the fully distributed cooperative tracking protocols, the adaptive law is also adopted to adjust the coupling weight. With the developed control laws,we can prove that all signals in the closed-loop systems are guaranteed to be uniformly ultimately bounded.Finally,a simple simulation example is provided to illustrate the established result.

I. INTRODUCTION

IN recent years, coordination problem of multi-agent systems has received a great deal of attention and become a heated topic due to the reason of its extensive applications in many areas, which include formation flight of UAV, collaborative rescue, multi-robot cooperative actions, distributed sensor networks and so on.Consensus problem is well-known as one of the foremost and basic issues in the area of coordination control for multi-agent systems, whose purpose is to develop distributed control protocols which make a group of agents reach an agreement on some quantities. There are many absorbing issues of coordination control linked with consensus such as synchronization, swarm, flock, formation,rendezvous, containment [1]. Till now, numerous constructive results have been obtained for the consensus problems with different agent dynamics including single integration system,double integration system,general linear system,discrete-time system, time-delay system, descriptor system, fractional-order system, nonlinear system [2]-[9].

As is known to all, neural networks (NNs) and fuzzy logic systems (FLSs) have been extensively used to model and design the control for uncertain interconnected (largescale)nonlinear systems. In [10]-[12], fuzzy decentralized control schemes have been developed for some classes of uncertain interconnected nonlinear systems. By assumption that the uncertainty can be linearly parameterised by a neural network,distributed consensus protocols were developed to solve multiagent problems in [13]-[18].

In comparison with integer-order systems, fractional-order systems are more suitable to model some practical application systems such as viscoelastic systems, dielectric polarization,electromagnetic waves and so on. It is easy to see that the traditional integer-order systems can be viewed as a special case of the fractional-order systems.In[19]-[21],the authors investigated the stability problem of fractional-order systems,which is more complex than that of integer-order systems.Recently, some researchers have focused on the coordination problem of fractional-order systems.The first-order consensus problem was generalized to the case of networked fractionalorder systems in [8]. The consensus problem of fractionalorder multi-agent systems with input delay and communication delay was studied by[22].In[23],the authors probed the consensus problem of fractional-order with uncertainty dynamics via output feedback protocol. The synchronization problem for a general fractional-order dynamical network model was addressed in [24]. In [25], the relative state error feedback laws were used to solve the leader-following fractional-order consensus problem with Lipschitz nonlinear dynamics. The leader-following consensus problem of fractional-order multiagent systems was addressed via adaptive pinning control by [26]. The multi-consensus problem of fractional-order uncertain linear multi-agent systems was investigated by [27],and the related containment problem was addressed by [28].

Generally, the above established consensus conditions are related to the interaction topology.The well-known consensus condition for the coupling parameters is determined by the smallest real part of the non-zero Laplacian eigenvalues of the interaction topology, which plays a key role in the consensus stability analysis. For a large-scale interaction topology, it is very hard to estimate its eigenvalues, which limits the applications of the obtained results [29]. Because the eigenvalues of the Laplacian matrix are the global information, strictly speaking, most of distributed consensus protocols proposed in the above references are not able to be implemented in the fully distributed way. To overcome this drawback, the distributed adaptive approaches are proposed to design the coupling parameters. The distributed adaptive state consensus protocols were provided by [29]. The adaptive state tracking protocol under directed interaction topology was proposed in[30]. The adaptive design approaches were put forward to solve second-order consensus problem with nonlinear dynamics in [3], [31]. To solve the flocking problem with nonholonomic mobile robots, the distributed adaptive formation tracking law was addressed in [32]. In [33], a distributed adaptive coupling parameter design approach was used to solve observer-based leader-following consensus problem with second-order nonlinear dynamics. Under undirected interaction topology, the distributed full-order observer-based adaptive consensus protocols were proposed to solve the linear consensus problem in [34].

Motivated by the above works, we investigate cooperative tracking problem of the fractional-order systems under undirected topology. By assumption that unknown nonlinear uncertain dynamics can be parameterized by a neural network,an adaptive learning law is proposed to deal with the unknown uncertainty. Based on the adaptive learning law, two kinds of cooperative tracking protocols are constructed in this paper.In comparison with the existed references,the main contributions are listed as follows: 1) Unlike most existing references of fractional-order multi-agent systems, which assume that all agents have identical dynamics, here the dynamics of each agent are assumed to be heterogeneous and have unknown nonlinear dynamics. To deal with the unknown nonlinearities,an adaptive learning law is proposed for each following agent,by which the consensus protocol for general linear multi-agent systems is generalized to solve fractional-order consensus problem. 2) Furthermore, an adaptive coupling weight law is proposed for each following agent, by which the proposed consensus protocols are implemented in the fully distributed fashion. 3) Obviously, our established result can be applied to the general linear multi-agent systems with uncertain dynamics directly. Even in this special case, our established result is novel, which generalizes the existed result.

The rest of the paper is organized as follows. In Section II,some basic concepts of the fractional-order systems and the formulation of our considered problem are introduced. Two kinds of distributed adaptive cooperative tracking protocols are proposed in Section III-A and III-B respectively, which contain our main result. Following that, a simulation example is provided in Section IV. Conclusions are given in Section V.

II. PRELIMINARIES AND PROBLEM FORMULATION

A. Notations and Interaction Topology

In this paper, the notations are standard. Rndenotesndimensional Euclidean space.‖·‖is Euclidean norms. Rn×mrepresents the set ofn×mreal matrices.INrepresents the identity matrix of dimensionN. 1n ∈Rnis the column vector with all components equal to one.Dαrepresentsαth order differintegration operator.A ＞0 means that matrixAis positive definite. For a matrixP ∈Rm×n, its minimum singular value is expressed asand maximum singular value is expressed astr{M}represents the trace of matrixM. diag{λ1),...,λn}is a diagonal matrix withλibeing theith diagonal element.?denotes Kronecker product which satisfies: 1)IfA ≥0 andB ≥0,then

The interaction topology is modeled by simple weighted graphwith node setedge setand a weighted adjacency matrixwith nonnegative weights.If(υi,υj)∈E,thenaij ＞0, andaij= 0 otherwise. The neighbor set of the nodeiis denoted byThe degree matrix of graphGisD=diag{d1,d2,...,dN}withThen,the Laplacian matrix ofGis defined asL=D-A, which satisfies

Here, the considered multi-agent system is composed ofNagents (labeled byυi,i= 1,2,...,N) and a leader (labeled byυ0), whose interaction topology is represented byWe use graphto depict the interaction topology among theNfollowing agents.The weighted constantbi,i=1,2,...,Nis taken as positive constant if agentiis connected to the leader and otherwise taken as zero. LetB=diag{b1,b2,...,bN}.DenoteWe always assume that the interaction topology satisfies the following assumption.

Assumption 1:The subgraphrelated with all the following agents is undirected and graphcontains a directed spanning tree with the leader as the root.

The weighted constantbi,i= 1,2,...,Nis taken as positive constant if agentiis connected to the leader and otherwise it is taken as zero. LetB=diag{b1,b2,...,bN}.DenoteH=L+B. MatrixHhas the following property defined by Lemma 1.

Lemma 1:Supposing that the graphGis undirected, fixed,and connected, and at least one agent has access to the leader.Then,His positive definite.

B. Fractional Calculus and Derivation

In this subsection, some basic concepts and properties of fractional integration and derivation are introduced.Fractionalorder calculus is a generalization of integration and differentiation to a non-integer fundamental operatorDα, which extends the specific definitions of the traditional integer-order to the more general arbitrary order context leading to different definitions for fractional derivatives [35]. Throughout this paper, letαbe a positive constant with 0＜α ＜1. Euler’s Gamma function is a basic function for the fractional calculus,which is denoted as

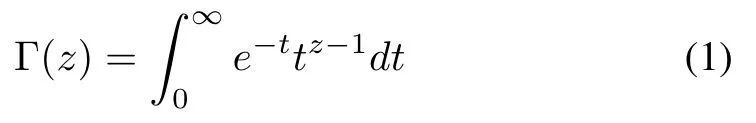
by which the Caputo fractional integral with orderαis defined as follows.

Definition 1 [35]:The definition of fractional integral of continuous function f(t)with respect to t and the terminal valuet0is given by

The fractional-order systems can be viewed as a generalization of integer-order systems. The following result of fractional-order systems will be used later.

Lemma 2:The fractional-order nonlinear differential equation

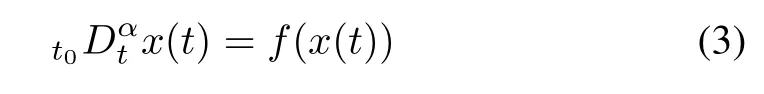
due to the continuous frequency distributed model of the fractional integrator, can be written as

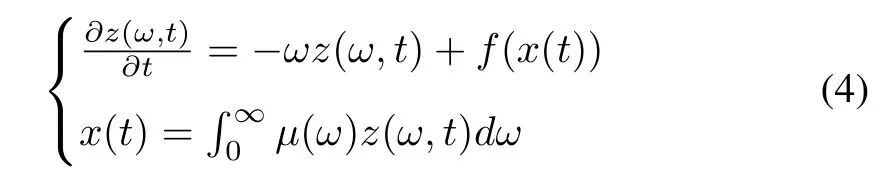
wherez(ω,t) is the infinite dimension distributed state variable andμ(ω) is defined as

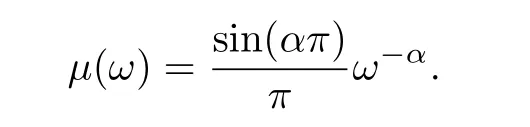
C. Problem Formulation

Consider the fractional-order multi-agent system consisting ofNfollowing agents and a leader. The dynamics ofNfollowing agents are described by

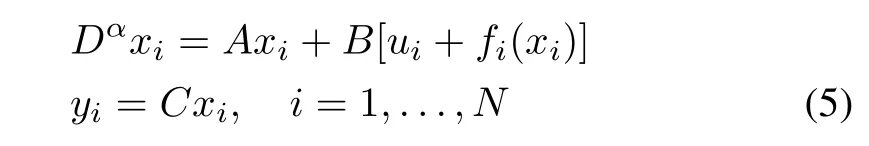
where 0＜α ＜1 donates the order of the fractional integration,xi ∈Rnis the state information of agenti,ui ∈Rmis its control input,fi(xi)∈Rmis unknown matched uncertain dynamics which contains bounded exogenous disturbances and unmodeled uncertainties.A ∈Rn×n,B ∈Rn×mandC ∈Rm×nare known system matrices.Throughout this paper,pair(A,B) is assumed to be stabilizable and (A,C) is assumed to be detectable.

The dynamics of leader agent is described by

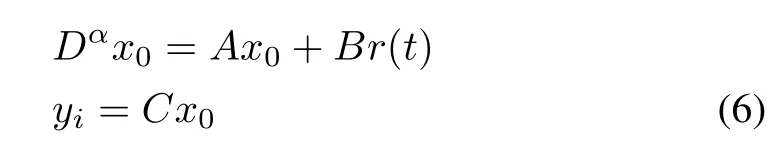
wherex0∈Rnis the leader state,r(t)∈Rmis expressed a bounded input .

Assumption 2:For all initial conditions, the solution ofx0exists.

We say that the multi-agent system achieves consensus if limt →∞(xi(t)-x0(t))=0,i=1,2,...,Nholds for any initial states. The main objective of this paper is to design a distributed protocolui(t)to solve the consensus problem,that is, the closed-loop multi-agent system achieves consensus.

To obtain the feedback gain matrix, the following wellknown result will be used.

Lemma 3 [36]:If (A,B) is stabilizable andQis a symmetric positive definite matrix, then there is a unique positive definite matrixPto satisfy the Riccati equation

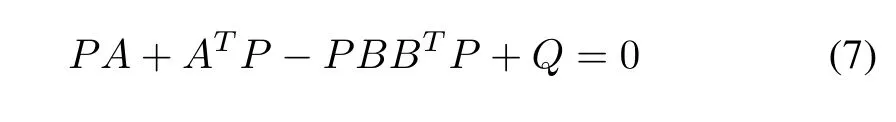
with any givenQ ＞0.

III. MAIN RESULTS

In this paper, it is assumed that each agent can obtain the state information of its neighbor agents. In order to solve the fractional-order multi-agent consensus problem with uncertain dynamics, the neural network learning law is adopted to deal with uncertain dynamics.

A. Cooperative Tracking With Learning Law

To begin with, leteibe relative state error between theith agent and its neighboring agents, which is denoted by

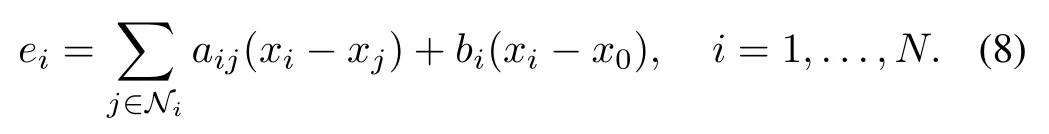
The tracking error is defined asδi=xi -x0. It follows from (5) and (6) that the dynamics forδican be expressed as

whereFi(xi)=fi(xi)-r(t).

Proceeding to the next step, the following assumption is necessary to construct the effective learning law against the unknown dynamicsFi.

Assumption 3:For the leader-following multi-agent systems(5) and (6), the related uncertain dynamicsFi(xi) can be parameterized by a neural network as follows:

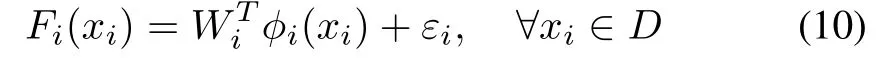
whereWi ∈Rs×mis an unknown constant weight matrix satisfyingwithWiS ∈R being a positive constant.φi(xi): Rn →Rsis a known neural basis function vectorsatisfyingwithφiS ∈R being a positive constant.εiis the approximation error satisfyingwithεiSa positive constant.D ?Rnis a sufficiently large domain.

Remark 1:The functionF(x) is defined as a smooth function. On condition thatxis restricted to a compact set,(10) holds for a large class of activation functions and the functional reconstruction errorεcan be made arbitrarily small by increasing the number of nodes in the network structure.This assumption is quite standard in the literatures, and more detail can be referred to [13]-[18]. According to [17], we can consider a dynamical model which contains the unknown matched uncertaintyωi(t) as follows:

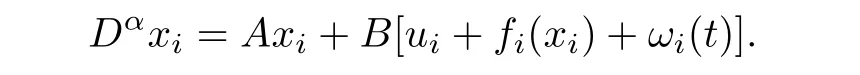
In this paper, the adopted control law is proposed for agentiwith form

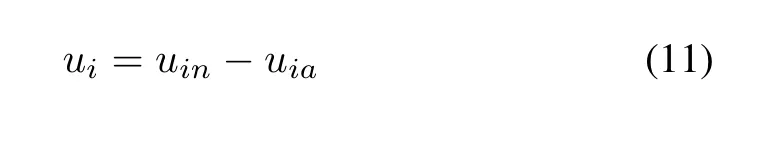
uinis taken as the following well-known linear cooperative control law

where positive constantcrepresents the coupling strength.To deal with uncertainties,uiais adopted to compensate the uncertainties, which is designed as

Substituting (11) into (9) yields

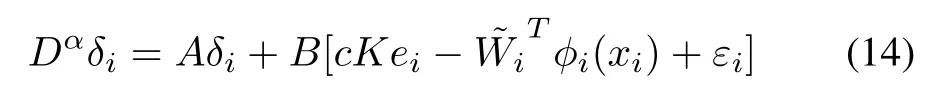
and the dynamics of neighborhood synchronization errorecan be described as

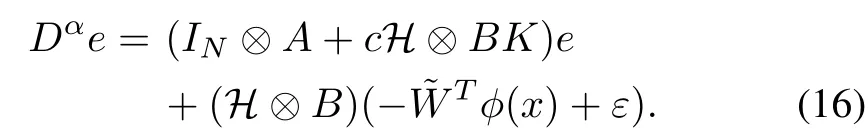
Now,the following result is established for the protocol(12)to solve the fractional-order consensus problem.

Theorem 1:For the fractional-order multi-agent systems(5)and(6),suppose that Assumptions 1-3 hold.Select the control law (11) withK=-BPand the coupling strengthcbeing satisfied with

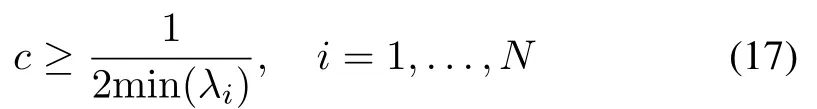
whereP ∈Rn×nis the unique positive matrix solution of Riccati equation (7) with any givenQ ＞0, andλiis theith eigenvalue of matrixH.is updated by

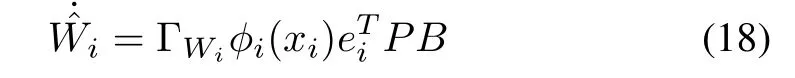
where ΓWi ∈R are given positive constants. Then, all signals in the closed-loop network are uniformly ultimately bounded,and the tracking error vectorδsatisfiesfor some constantγ1∈R+.

Proof:It follows from Lemma 2 that the fractional-order tracking dynamical system (15) can be expressed as

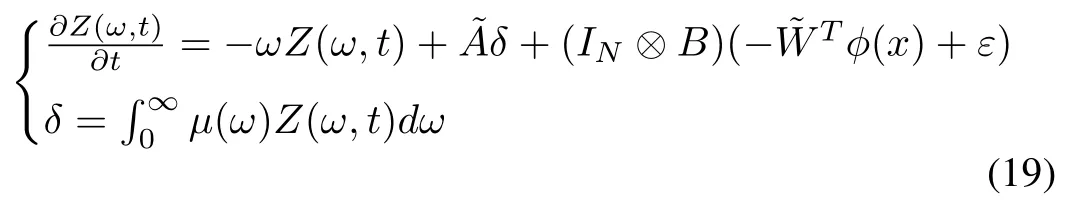
Consider the following Lyapunov function

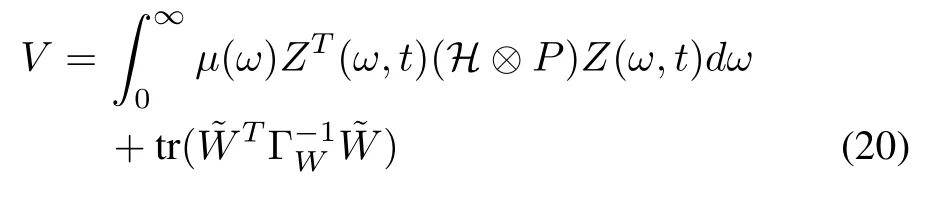
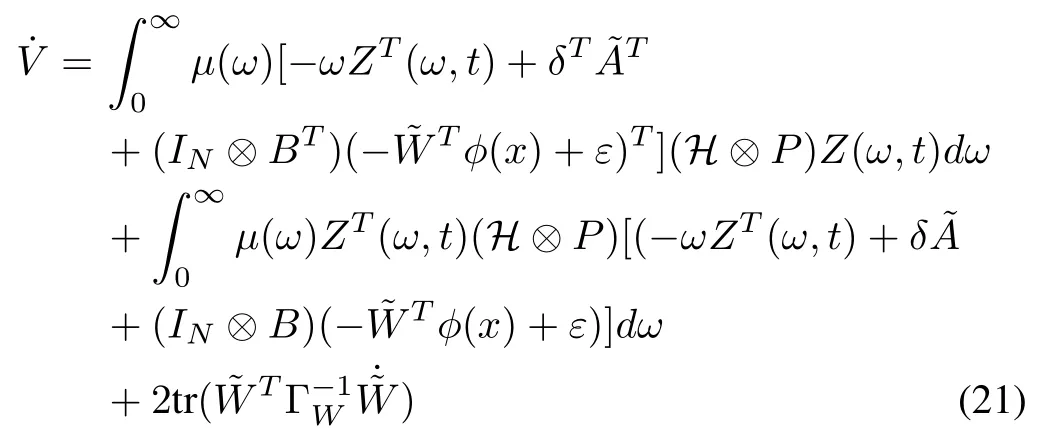
which can be simplified as

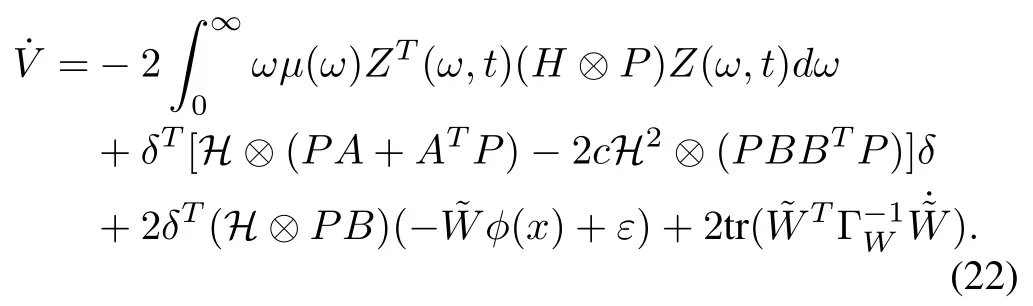
Substituting the adaptive law (18) into (22), we can get

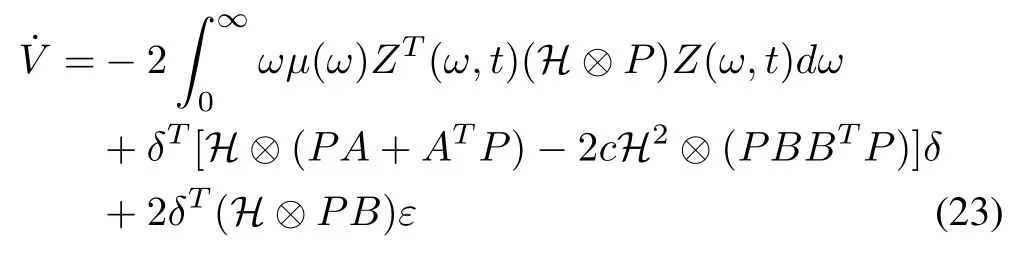
from which we can obtain

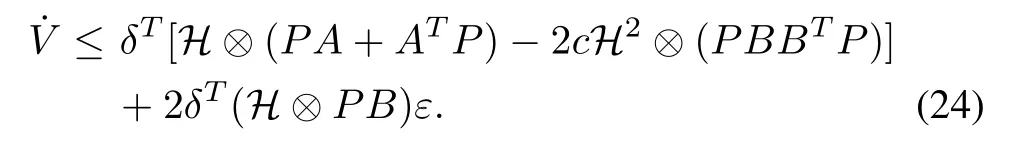
According to Lemma 1,His a positive definite matrix.Thus,there must exist a unitary matrixUsuch thatUT HU=diag(λi),i=1,...,N. Take a state transformationζ=(UT?I)δwithζ=[ζ1,...,ζN]T. Then, it follows from (24) that one has

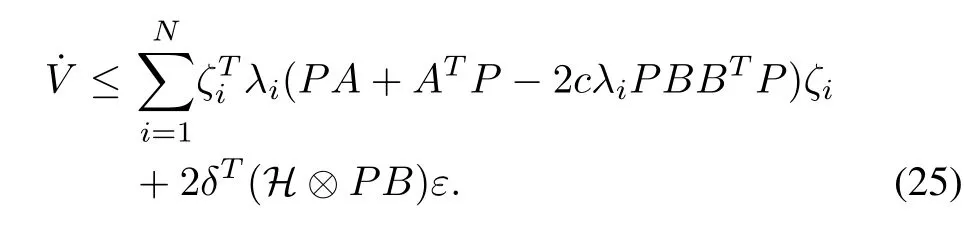
By means of (7) and (17), we have

According to Assumption 3,there exist constantsφS ∈R+,εS ∈R+such that‖φ(x)‖ ≤φS,‖ε‖ ≤εS. Then, we can obtain

with

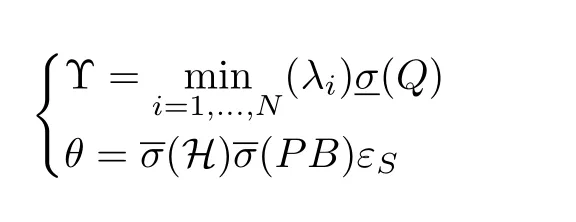
from which we know that ifthenThus,δis uniformly ultimately bounded,and limt→∞‖δ‖≤γ1with

Remark 2:Note that the protocol(12)is well-known,which is used to solve the consensus problem without uncertainties,that is,the case thatFi(xi)=0.To deal with uncertaintiesFi,the termuiain control law (11) is adopted to compensate the uncertainties.By(26),ifε=0,we havewhich means that limt→∞‖δ‖=0, that is, the multi-agent system achieves consensus. Non-zeroεimplies thatuiacannot compensate the uncertaintiesFicompletely. Thus, we obtain that the tracking error is bounded in this case. Note that the coupling weightcis relying on the smallest eigenvalue ofH, which belongs to the global information. From this point, although the linear control input (12) and the learning law (18) are based on the local state information, the consensus protocol(11) cannot be implemented in a fully distributed fashion.The fully distributed protocol problem is discussed in the next subsection.

Remark 3:Similar protocols of (10) have been adopted to solve the tracking problem of general nonlinear multiagent systems in [17]. Here, the protocols are generalized to solve the fractional-order systems with unknown nonlinear dynamics. Our adopted learning law (18) forWiis different from that of [17]. The following learning law is used in [17]

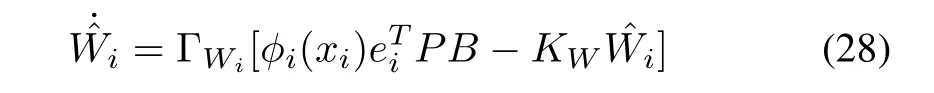
whereKWis a positive constant. While multi-agent system achieves consensus, we know that alleitend to zero. In this case, ?Wiwill tend to zero. Unfortunately, because of the existence of uncertaintiesFi,Wimay not be zero. Thus, the consensus is not easy to be achieved by learning law (28).In our simulation computation,we also find this phenomenon.For simplicity,ΓWiin(18)is taken positive constant.It is also feasible to take positive definite matrix ΓWiin learning law(18).

B. Fully Distributed Cooperative Tracking With Learning

To construct fully distributed protocol, an adaptive law for coupling weightcis proposed for each following agent.Then,the consensus protocol (11) is modified as follows:

whereuiais same as (13), an adaptive coupling strengthci ∈R is chosen by

witheiis defined as (8).

Similarly, by the protocol (29), the closed-loop multi-agent system can be written as

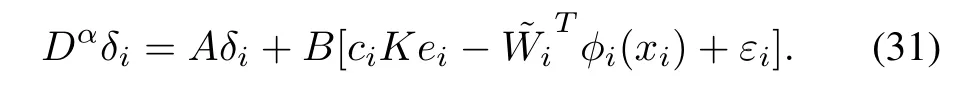
Then, the error dynamics of (31) can be expressed as

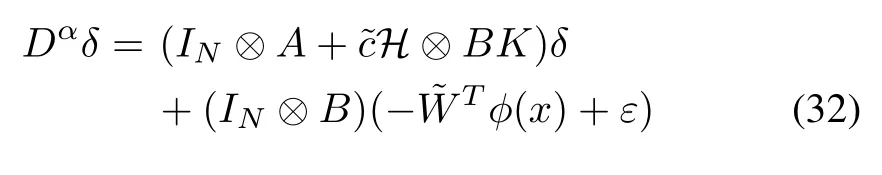
Theorem 2:For the fractional-order multi-agent systems(5)and (6), suppose that Assumptions (1)-(3) hold. Select the control law (29) together with (30) withK=-BPand Γθ=PBBT P, whereP ∈Rn×nis the unique positive matrix solution of Riccati equation (7) with any givenQ ＞0.The updating lawis chosen as (18). Then, all signals in the closed-loop network are uniformly ultimately bounded,and the tracking error vectorδsatisfies limt→∞‖δ‖≤γ2for some constantγ2∈R+.

Proof:It follows from Lemma 2 that the fractional-order tracking dynamical system (32) can be expressed as

Consider the following Lyapunov function

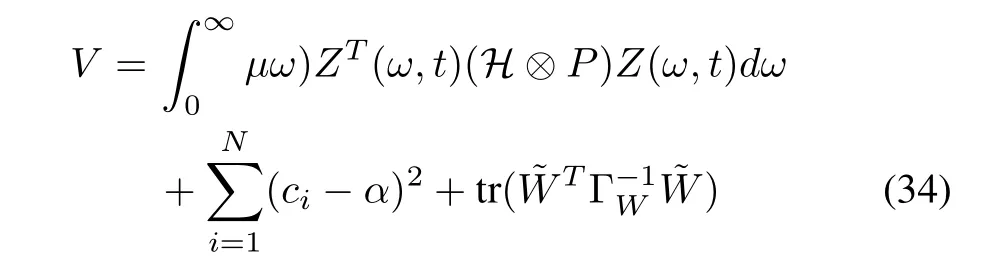
whereαis a sufficiently large positive constant.

The time derivative ofV(t) along (33) is given by

from which we can obtain

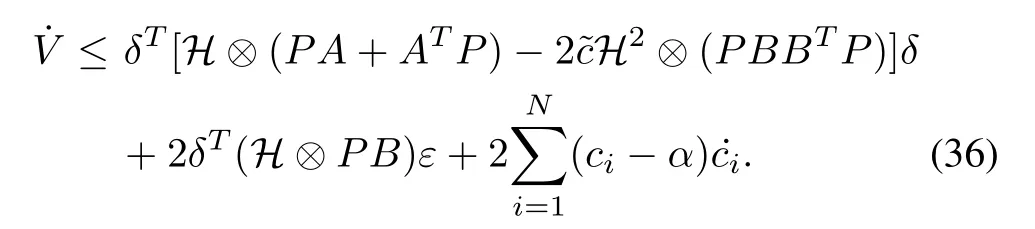
It follows from (8) and (30) that we can obtain

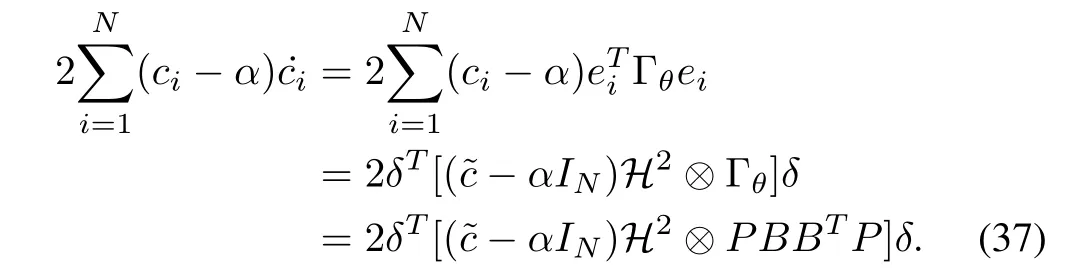
Then, substituting (37) into (36), we have

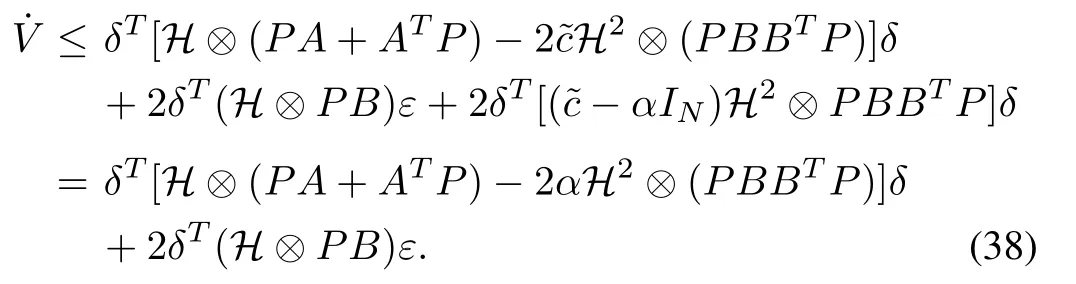
According to Lemma 1, we can know thatHis a positive matrix. LetUbe a unitary matrix such thatUT HU=diag(λi),i=1,...,N. Take a state transformationζ=(UT?I)δwithThen, by (38), we can get

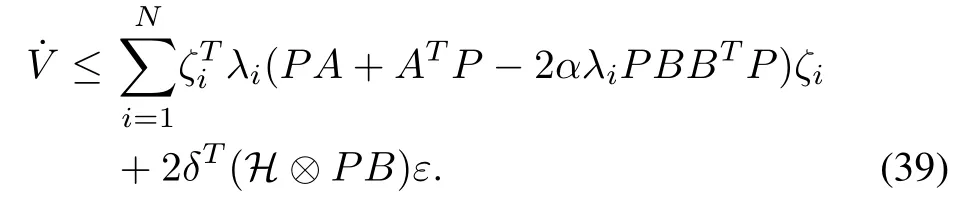
Choosing large enough positive constantαsuch that for alli=1,...,N, 2αλi ≥1 holds, we can obtain

Similarly as Theorem 1, letandFrom (40), we can obtain

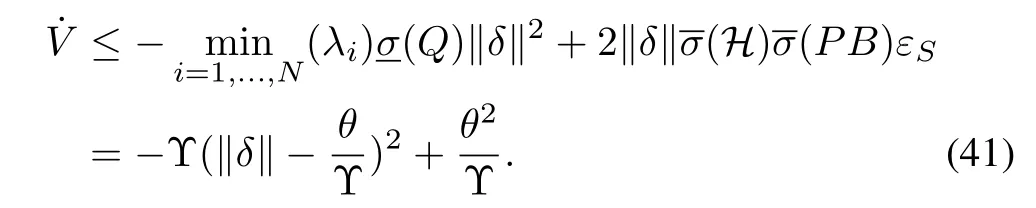
Thus, we know that whenThus,δis uniformly ultimately bounded, andwithγ2

Remark 4:Since the coupling weightcis involved in protocol(11),the consensus is dependent on the global information of the interaction topology. To overcome this shortcoming,an adaptive coupling weight law (30) is proposed for each following agent, by which the proposed consensus protocols are implemented in a fully distributed fashion. Whileε= 0,it follows from (40) that we havefrom which we can obtain thatthat is, the multi-agent system achieves consensus. Furthermore, we haveAccording to(30),ciis monotonously increasing.Thus,ciwill converge to a constant in this case. When the errorεis not zero,the multi-agent system may not achieve consensus.Thus,the neighborhood synchronization erroreimay not converge to zero, which may leadciincreasing too large. To solve the problem, we can take a large enough thresholdcmax. Ifciincreases greater thancmax, takeci=cmax.

Remark 5:Although it is assumed that 0＜ α ＜1,all result is also true forα= 1, that is, our established result can be applied to the general linear multi-agent systems directly. Thus, even in general nonlinear multi-agent systems,the protocol (29) also generalizes the existed result of [17].

IV. NUMERICAL EXAMPLE

In this section, a simple example is provided to illustrate the obtained theoretical results. Consider an electrical circuit system,which is composed of resistors,supercondensators(ultracapacitors),coils,and voltage sources.It is widely assumed that the currentiC(t) and voltageuC(t) of supercondensator satisfy

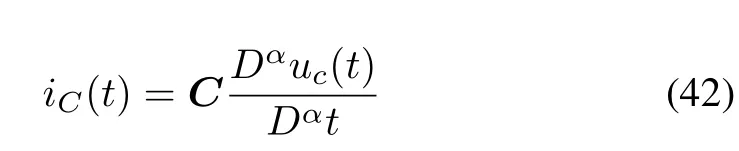
where 0＜α ＜1, andCis the capacity of the supercondensator. The voltageuL(t) and its currentiL(t) of the coil satisfy

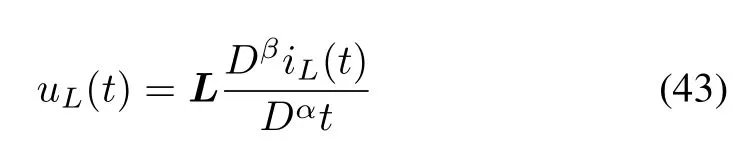
where 0＜ β ＜1, andLis the inductance constant. A simple electrical circuit system was provided by [38], which is modeled by a fractional-order system as follows

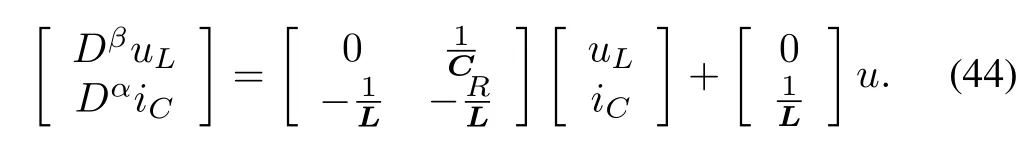
More detail can be referenced to [38] and [39].

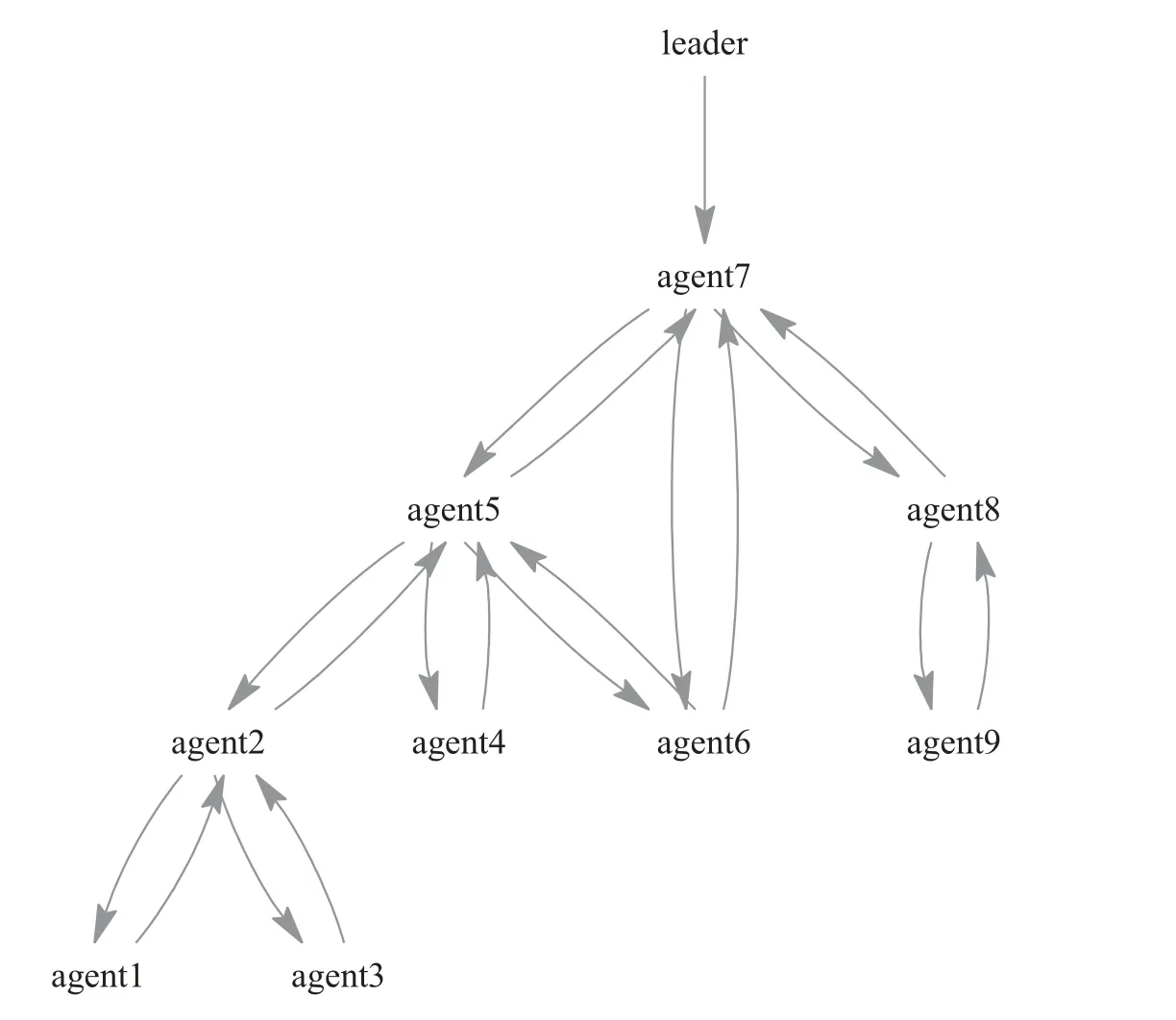
For convenience, takeα=β= 0.8. LetSince there always exist the modeling error and disturbance,we consider a network of electrical circuits consisting ofN= 9 following agents and a leader. The dynamics of following agents and leader agent are assume to be modeled by (5) and (6) respectively, whose system matrices are given by

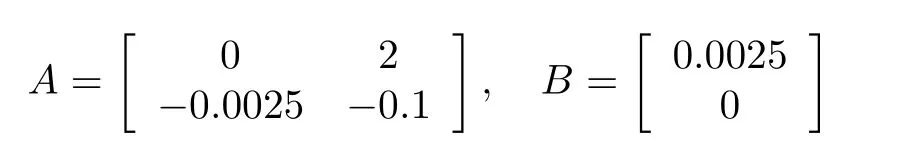
and the order of fractional system is taken asα= 0.8. For simplicity,taker(t)=sin(t),the unknown nonlinear function can be approximated byFi(xi) =ai1sin(xi1)+ai2cos(xi2),whose unknown constants can be taken asai1=2,ai2=2.

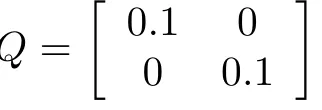
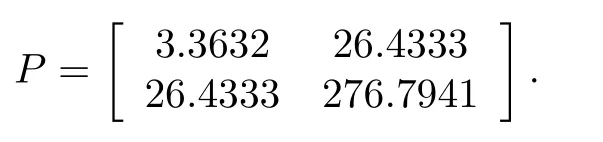
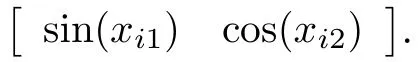
The parameters ΓWiused in (18) are taken as ΓWi=100.

Then, the feedback matrixKcan be constructed by

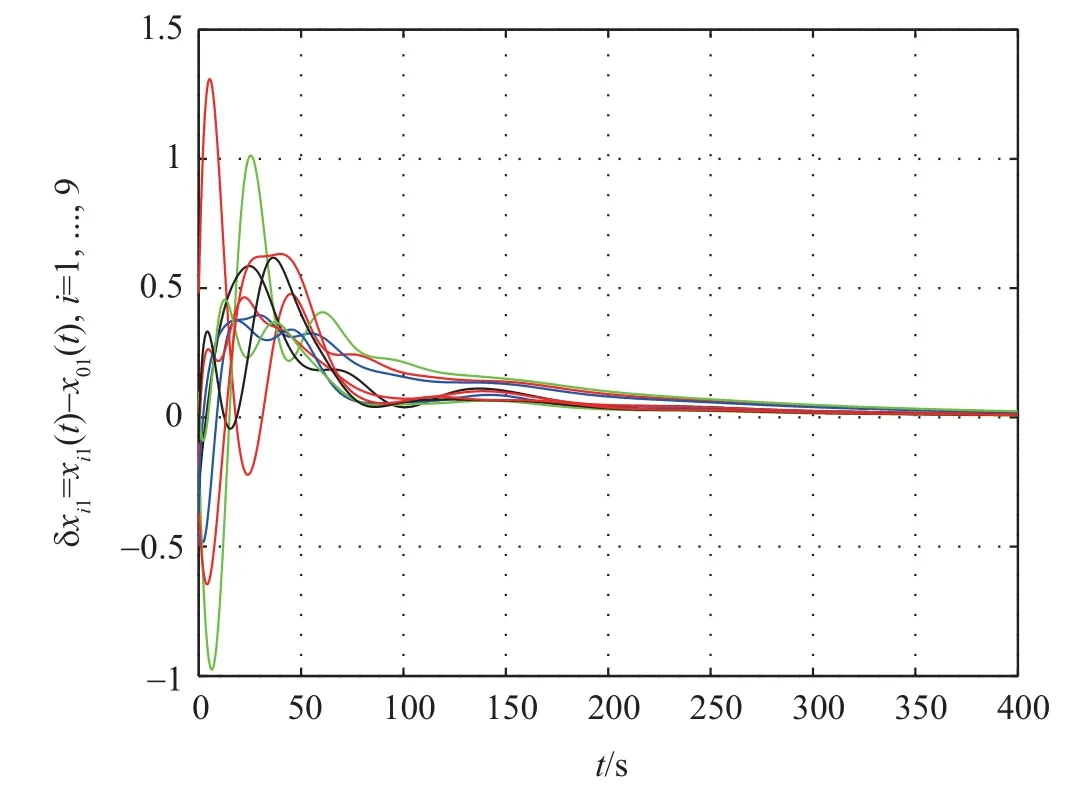
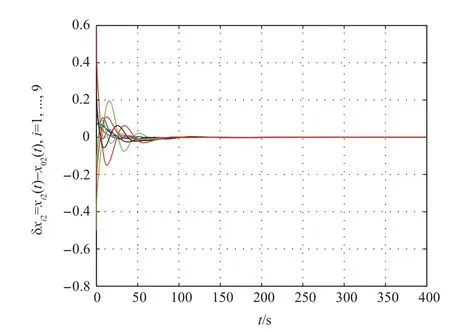
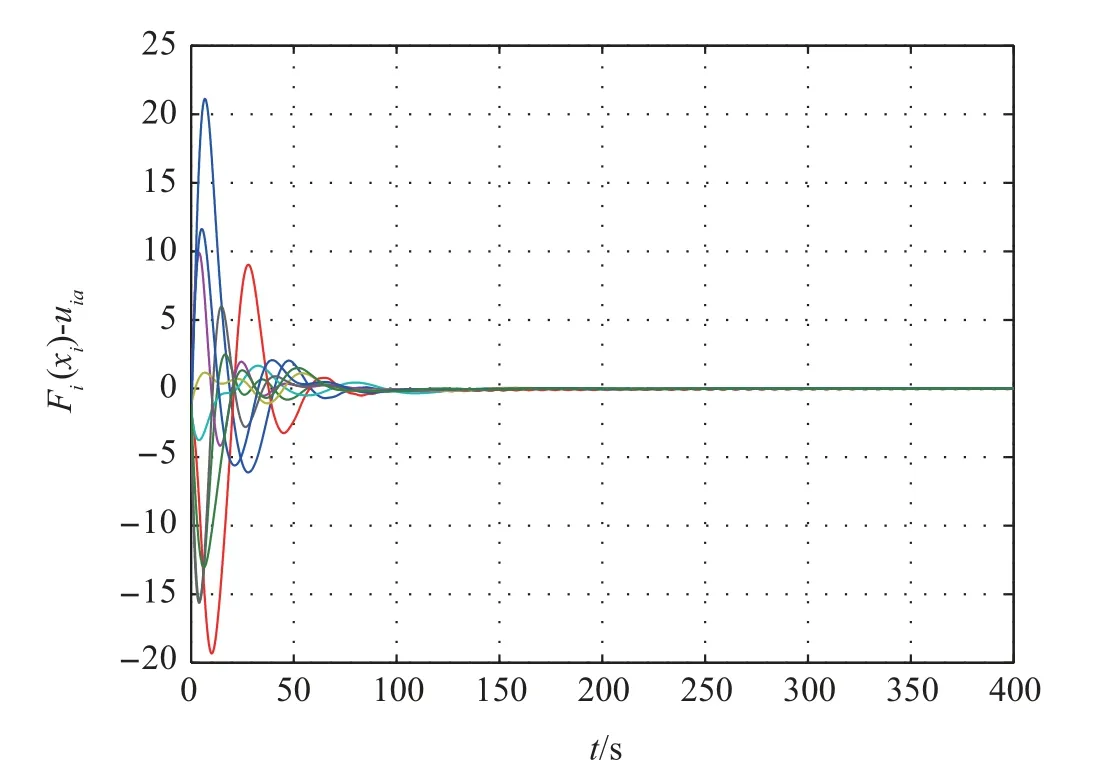
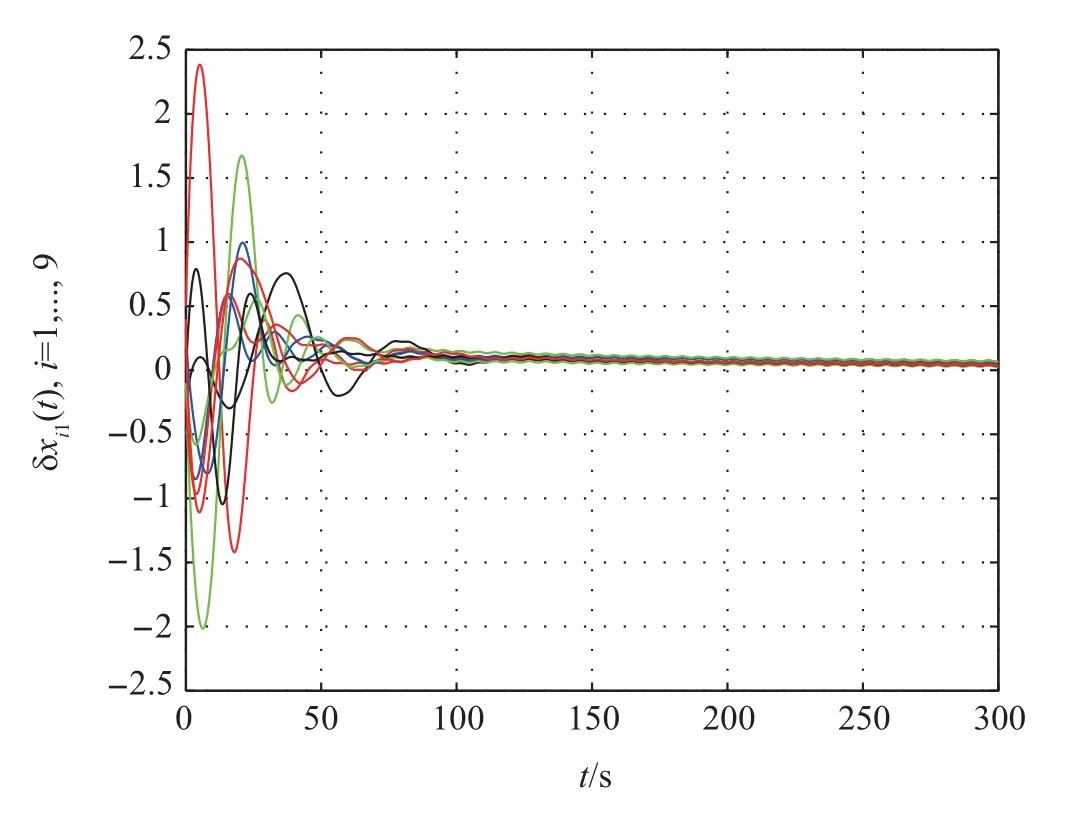
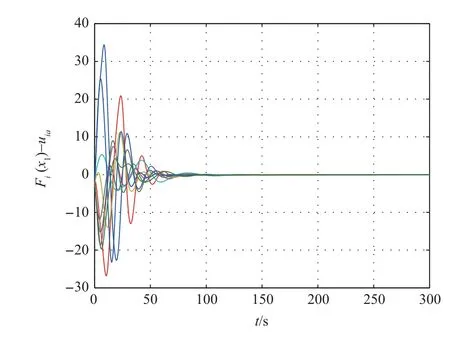
Firstly,the consensus protocol(11)is used to solve consensus problem. The first and the second components of tracking errorsδi=xi-x0are shown in Figs. 2 and 3, respectively,which show that the multi-agent system can achieve consensus.Moreover,the approximation errors of nonlinear dynamics are shown in Fig.4, which shows that the learning law (18) is effective to estimate the weightWi. When the small coupling strengthcis taken, the simulation result shows that the multiagent system cannot achieve consensus.

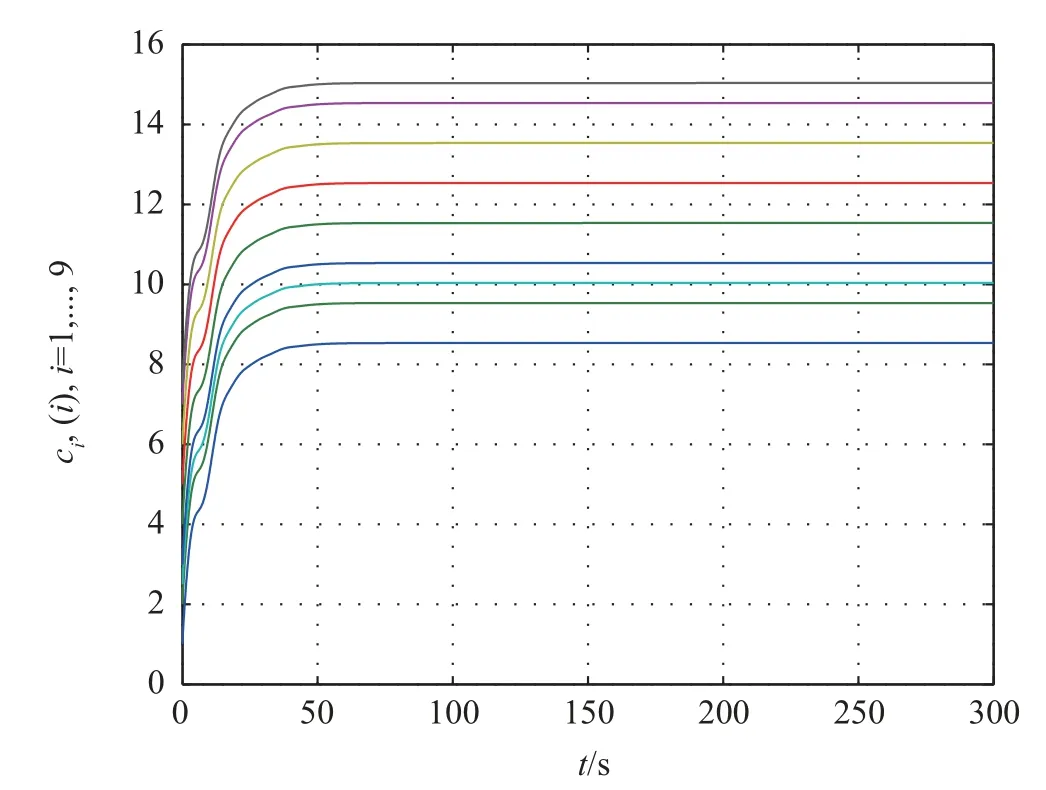
While the consensus protocol (29) is used to solve consensus problem, the first and the second components of tracking errorsδi=xi-x0are shown in Figs. 5 and 6, respectively,which show that the multi-agent system can achieve consensus.The evolutions of approximation errors of nonlinear dynamics in Fig.7, which show that the learning law (18) is effective to estimate the weightWi. The adaptive coupling gains are depicted in Fig.8, from which we can know that the coupling weights converge to finite steady-state values.By adopting the consensus protocol (29), we can take very small initial value forci.

V. CONCLUSIONS

In this paper, we considered the cooperative tracking of fractional-order multi-agent systems with unknown nonlinear dynamics under undirected interaction topology. By assumption that unknown nonlinear dynamics can be parameterized by a neural network, adaptive learning laws were proposed to deal with unknown nonlinear dynamics. Then, a cooperative tracking protocol was generalized to solve the cooperative tracking problem of fractional-order multi-agent systems. To get the fully distributed cooperative tracking protocol, the adaptive laws were used to adjust the coupling weight. It is mathematically proved that with the developed controllers,all signals in the closed-loop network are guaranteed to be uniformly ultimately bounded. Future work will be focused on the adaptive protocols under directed interaction topology and time-delay cases.