On Uniqueness Problem of Meromorphic Functions Sharing Values with Their q-shifts

ZHANG Shui-ying, LIU Hui-fang

(College of Mathematics and Information Science, Jiangxi Normal University, Nanchang,330022)

Abstract: In this paper, the uniqueness problems on meromorphic function f(z) of zero order sharing values with their q-shift f(qz +c) are studied. It is shown that if f(z) and f(qz+c) share one values CM and IM respectively, or share four values partially, then they are identical under an appropriate deficiency assumption.

Key words: Meromorphic Function; Uniqueness; Shared Value; Shift

§1. Introduction and Main Results

In this paper, we adopt the standard notations and basic results of Nevanlinna’s value distribution theory of meromorphic functions as explained in [1-3]. In the following, the term meromorphic function will mean meromorphic in the whole complex plane C.

Let f be a meromorphic function, we denote by S(r,f) any quantity satisfying S(r,f) =o(T(r,f))(r →∞,r), where E is a set of finite logarithmic measure. A meromorphic function ω is called a small function of f provided that T(r,ω) = S(r,f). The family of all small functions of f is denoted by S(f) andIn addition, we denote by S1(r,f) any quantity satisfying S1(r,f) = o(T(r,f))(r →∞,r ∈H), where H is a set of logarithmic density 1. It is obvious that S(r,f)=S1(r,f) and S1(r,f)+S1(r,f)=S1(r,f).

Let f and g be two nonconstant meromorphic functions, a ∈C∞=, and letdenote the set of distinct a-points of f(z). We say that f and g share a IM, ifIf f and g have the same a-points with the same multiplicity, then we say that f and g share a CM.

The famous five-valued theorem and four-valued theorem due to Nevanlinna[4]show that if two nonconstant meromorphic functions f and g share five distinct values IM,then f(z)≡g(z);if f and g share four distinct values CM, then f is a M¨obius map of g. Gundersen [5-6]extended the four-valued theorem to the case “3CM+1IM=4CM” and “2CM+2IM=4CM”.But until now, “1CM+3IM” is still an open problem. Especially, for the case g(z)=f(z+c),Heittokangas, Korhonen and Laine et al.[7] proved the following result.

Theorem A[7]Let f be a meromorphic function of finite order, c ∈C {0}, and let α1,α2,α3∈be three distinct periodic functions with period c. If f(z) and f(z+c) share α1,α2CM and α3IM, then f(z)≡f(z+c).

Theorem A is improved by replacing the shared value condition“2CM+1IM”with“1CM+1IM”as follows.

Theorem B[7]Let f be a meromorphic function of finite order, c ∈C {0}, and let α1,α2,α3∈be three distinct periodic functions with period c. If f(z) and f(z+c) share α1CM and α3IM, and if

then f(z)≡f(z+c).

In 2013,the authors in[8]investigated the shared values of meromorphic functions and their q-shifts, and obtained the similar result to Theorem A.

Theorem C[8]Let f be a meromorphic function of zero order, q ∈C{0,1},c ∈C{0},and let a1,a2,a3∈C∞be three distinct values. If f(z) and f(qz+c) share a1,a2CM and a3IM, then f(z)≡f(qz+c) and |q|=1.

In this paper, we reduce the shared value condition “2CM+1IM” in Theorem C to the case“1CM+1IM” , and obtain the following result.

Theorem 1.1Let f be a nonconstant meromorphic function of zero order, q ∈C {0,1},c ∈C, and let a1,a2,a3∈C∞be three distinct values. If f(z) and f(qz+c) share a1CM and a2IM, and if

then f(z)≡f(qz+c) and |q|=1.

Recently, Charak, Korhonen and Kumar [9] investigated the uniqueness of meromorphic functions sharing values partially with their shifts, and obtained the following result.

Theorem D[9]Let f be a meromorphic function of hyper-order less than 1,c ∈C{0}. Let α1,α2,α3,α4∈be distinct periodic functions with period c such that,f(z+c)?αj(z))(j =1,··· ,4). and δ(a,f)>0 for some a ∈, then f(z)f(z+c).

Inspired by this result, we study the uniqueness of meromorphic functions sharing values partially with their q-shifts, and obtain the following results.

Theorem 1.2Let f be a nonconstant meromorphic function of zero order, and let q ∈C{0,1},c ∈C. Iffor distinct values ak∈C∞(k =1,··· ,4),and δ(a,f)>0 for some a ∈C∞, then f(z)≡f(qz+c) and |q|=1.

Theorem 1.3Let f be a nonconstant meromorphic function of zero order, and let q ∈C{0,1},c ∈C. Iffor distinct values ak∈C∞(k =1,··· ,4),and(r,a,f(z),f(qz+c))S1(r,f)for some a ∈C∞{a1,a2,a3,a4}, then f(z)f(qz+c)and |q| = 1, where(r,a,f(z),f(qz+c)) denotes the counting function of common a-points f(z) and f(qz+c), each counted only once.

Remark 1.1Theorem 1.1–1.3 also hold for c=0.

§2. Lemmas

In order to prove the above Theorems, we need the following lemmas.

Lemma 2.1[8,10?11]Let f be meromorphic function of zero order, q ∈C{0,1},c ∈C,then

Remark 2.1For c = 0, the first equality in Lemma 2.1 is the logarithmic derivative lemma of q-difference, which is from reference [10], the other two equalities are from reference[11]. For c0, Lemma 2.1 is from reference [8].

Lemma 2.2[8,10]Let f be a meromorphic function of zero order, q ∈C{0,1},c ∈C,and let a1,···ap∈C be p(≥2) distinct values, then

where Npair(r,f)=2N(r,f)?

Remark 2.2For c=0, Lemma 2.2 is the second main theorem of q-difference, which is from refer ence [10]. For c0, Lemma 2.2 is from reference [8].

Lemma 2.3Let f be a nonconstant meromorphic function of zero order, and let q ∈C{0,1},c ∈C. If f(z)f(qz+c), then |q|=1.

ProofNow we divide two cases to complete the proof.

Case 1Suppose that f is a nonconstant rational function. Let

where an(0),···,a0,bm(0),···,b0are complex numbers. From f(z)≡f(qz+c) and (2.1),it follows that

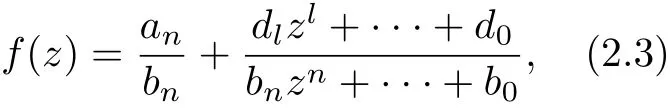
where l(≤n ?1) is a nonnegative integer,dl(0),··· ,d0are complex numbers. From f(z) ≡f(qz+c) and (2.3), it follows that

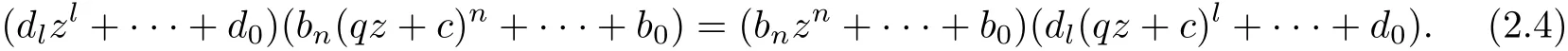
Then from (2.4), we get qn?l=1. So we have |q|=1.

Case 2Suppose that f is a transcendental meromorphic function. From the fact that f is transcendental of zero order, it follows that at least one of the sets of zeros and poles of f(z)is infinite. Without loss of generality,we assume that f has infinite many zeros. Let z0(0)be a zero of f(z), then from f(z)≡f(qz+c), we get a sequence{bn=qnz0+qn?1c+···+qc+c}such that f(bn) = 0. If |q| < 1, thenis an accumulation point of the sequence {bn}. This is absurd. If |q|>1, take sufficiently large r such that |bn?1|≤r <|bn|, then we have

which contradicts σ(f)=0. So we get |q|=1.

Lemma 2.4Let f(z) be a meromorphic function of zero order, q ∈C{0,1},c ∈C, and let a1,a2,a3,a4∈C∞be distinct values. Ifthen

(i)

(ii)

where d ∈C∞{a1,a2,a3,a4}.

Proof(i)Without loss of generality,we assume that a1,a2,a3,a4∈C. Since,f(z))?,f(qz+c))(k =1,··· ,4), we get

Then from the second main theorem due to Nevanlinna, Lemma 2.1 and (2.5), we get

The conclusion (i) is thus proved.

(ii)From the second main theorem due to Nevanlinna and the conclusion (i), we get

which implies

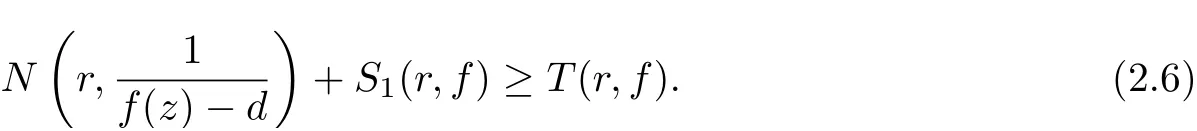
Since

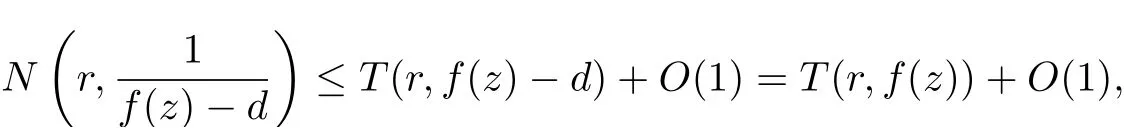
then combining with (2.6), we get

The conclusion (ii) is thus proved.

Lemma 2.5[7]Let f(z)be a meromorphic function,let ε>0,and let a1,a2,a3be pairwise distinct meromorphic functions such that a1,a2∈S(f) and

Lemma 2.6[12]Let f and g be nonconstant meromorphic functions, ak(k =1,··· ,5) be five distinct elements in, then

§3. Proofs of Results

Proof [Proof of Theorem 1.1]

Firstly, we consider the case that a1,a2,a3are all finite values. Suppose that f(z)f(qz+c), let

then

From (3.1) and (3.2), we know that g(z) and g(qz+c) share 0 CM and 1 IM, and

which implies

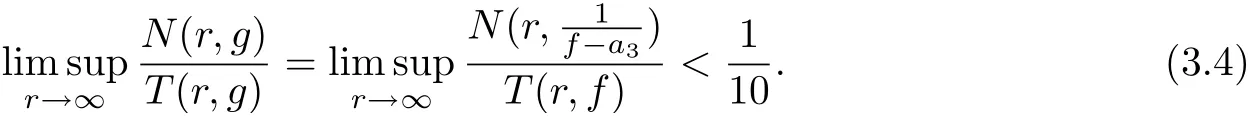
So from (3.4), there exists a real number ν ∈(0,), such that for sufficiently large r, we have

Let

From Lemma 2.1, we get

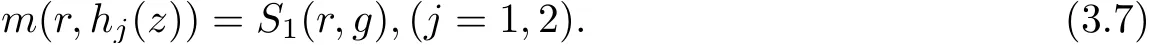
It follows from the expression of h1that the possible poles of h1(z) come from the zeros of g(z)and the poles of g(qz+c). Since g(z) and g(qz+c) share 0 CM, the zeros of g(z) can not be the poles of h1(z). So from Lemma 2.1 and (3.5), we get

Combining with (3.7) and (3.8), we get

On the other hand, from (3.6), we get

Then combining with (3.9) and (3.10), we get

which implies

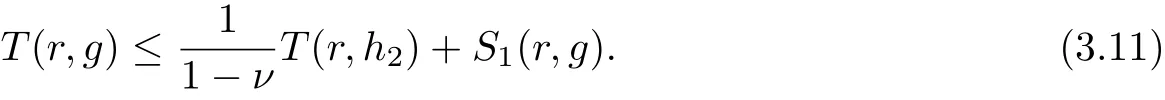
Since g(z) and g(qz+c) share 1 IM, the zeros of g(z)?1 and g(qz+c) must be the zeros of h1(z)?1. Then combining with (3.9), we get

Hence from the expression of h2, Lemma 2.1, (3.5), (3.6) and (3.12), we get

On the other hand, from (3.9) and (3.11), we get

which implies

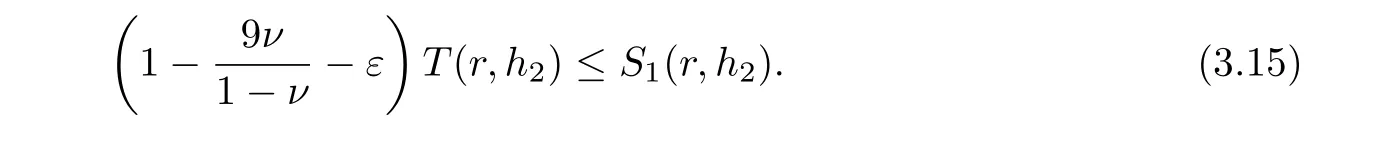
Secondly, we consider the case that one of a1, a2, a3is equal to ∞. Without loss of generality, we assume that a1=∞, take d ∈C{a2,a3}, and let

then F(z) and F(qz+c) share 0 CM and b2IM, and

Hence from the above proof, we get F(z)≡F(qz+c), which implies f(z)≡f(qz+c).

Finally, it follows form Lemma 2.3 that |q|=1. Theorem 1.1 is thus proved.

Proof [Proof of Theorem 1.2]

Without loss of generality, we assume that ak(k = 1,2,3,4) are all finite values. Suppose that, it follows that

Then from the second main theorem due to Nevanlinna and (3.16), we get

On the other hand, from Lemma 2.1, we get

Hence from (3.17), (3.18) and Lemma 2.2, we get

It follows from (3.19) that

which implies

So for each ak(k =1,2,3,4), we have

which implies δ(ak,f) = 0 for each ak(k = 1,2,3,4). For the case a ∈C∞{a1,a2,a3,a4}, it follows from Lemma 2.4 that

So δ(a,f)=0 also holds. This contradicts the assumption in Theorem 1.2.

If among ak(k = 1,2,3,4), there exists one, such as a4, is equal to ∞, then take d ∈C{a1,a2,a3} and let

Proof [Proof of Theorem 1.3]

Then combining with Lemma 2.1, we get

Take a ∈C∞{a1,a2,a3,a4}, from Lemma 2.6 and (3.23), we get

This contradicts the assumption in Theorem 1.3. So we get f(z) ≡f(qz +c). Then from Lemma 2.3, we get |q|=1. Theorem 1.3 is thus proved.