A Regularity Criterion Via the Pressure On the Three-dimensional Boussinesq Fluid Equations
LI Xiao, LI Ying-chao
(Huanghe Jiaotong University, Henan, 454000, China)
Abstract: In this paper, we investigate the regularity criterion via the pressure of weak solutions to the Boussinesq fluid equations in three dimensions. We obtain that for≤≤γ ≤3 if ?3π ∈Lγ(0,T;Lq), then the weak solution (u,θ) is regular on (0,T].
Key words: Boussinesq fluid equations; pressure; partial derivative
§1. Introduction
In this paper we consider the regularity criterion of weak solutions for the incompressible Boussinesq fluid equations in terms of pressure in three dimensions:
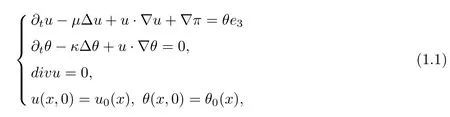
where u = (u1(x,t),u2(x,t),u3(x,t)) denote the unknown velocity vector field at a point x ∈R3and time t ∈[0,T); θ = (θ1(x,t),θ2(x,t),θ3(x,t)) and π = π(x,t) stand for the scalar temperature and the pressure, respectively. u0and θ0are the prescribed initial data for the velocity and the scalar temperature with property divu0=0. μ is the kinematic viscosity, κ is the thermal diffusivity.
The Boussinesq equations describes the evolution of the velocity field u for a three-dimensional incompressible fluid moving under the gravity and the earth rotation which come from atmospheric or oceanographic turbulence where rotation and stratification play an important role.
When the temperature field θ =0, (1.1) reduces to the incompressible Navier-Stokes equations:
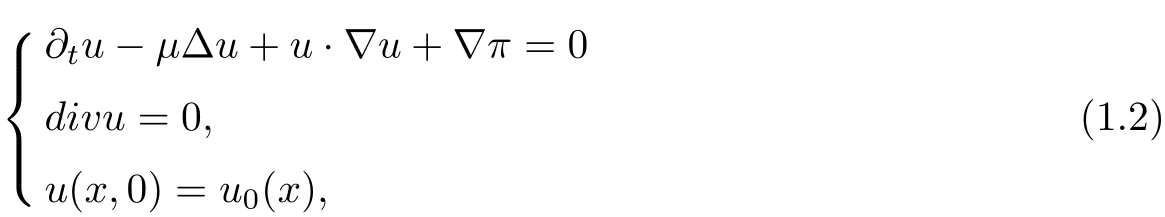
which has been greatly analyzed, see, for example, the classical books by Ladyzhenskaya [12],Temam [16], Lions [14] or Lemari′e-Rieusset [13].
Besides their physical applications, the Boussinesq fluid equations are also mathematically significant. In the three-dimensional case, the same as the classic Navier-Stokes equations, the question of global regularity of the weak solutions and the existence of global strong solutions of the Boussinesq equations are still the challenging open problems. It is of importance on the study of regularity of the weak solutions under additional critical growth conditions on the velocity or the pressure. So there are a lot of literatures devoted to find sufficient conditions to ensure smoothness, and many interesting results have been obtained(see, for example, [4-6,8-10] and references therein).
The purpose of this paper is to study the regularity via the pressure of weak solutions to the Boussinesq fluid system (1.1). Dong, Jia and Chen [6] established the velocity regularity in terms of the pressure in general Besov spaces.
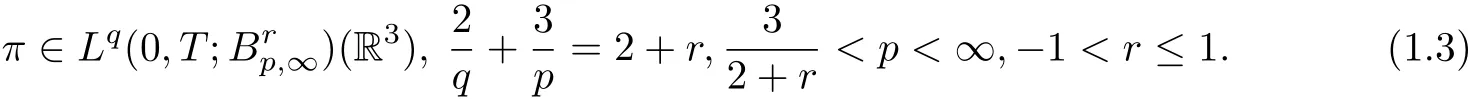
Very recently, Dong, Song and Zhang [6] showed the following regularity criterion for the 3D Boussinesq system with zero heat conductivity:
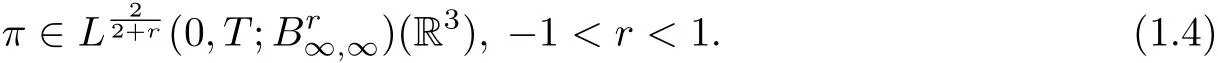
Further He and Fan [11] refined 1.4 as follows
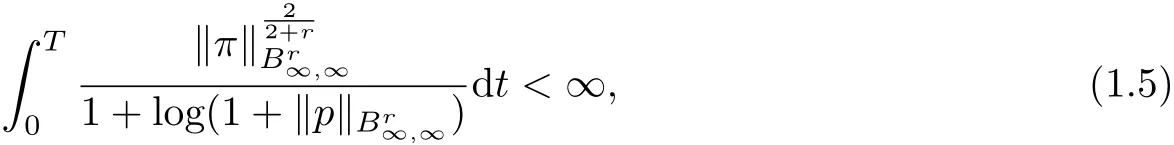
Inthe end-point case, Fuand Cai [7] refined 1.4 as follows

Particularly,Mechdene and Gala,Guo and Ragusa[15]considered the logarithmically regularity criterion of the Boussinesq system in terms of the partial derivative of pressure when
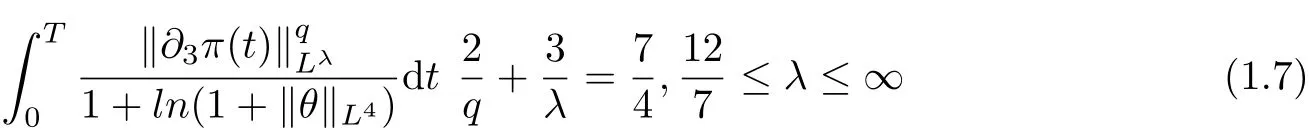
Motivated by the reference mentioned above, the purpose of the present paper is to extend the regularity of weak solutions to the 3D Boussinesq fluid equations (1.1) in terms of partial derivative of pressure.
Before stating our main results we introduce some function spaces and notations. Letdenote the set of all C∞vector functions f(x) = (f1(x),f2(x),f3(x)) with compact support such that divf(x)=0. Lrσ(R3) is the closure of C∞0,σ(R3)-function with respect to the Lr-norm·r for 1 ≤r ≤∞. Hsσ(R3) denotes the closure of(R3) with respect to the Hs-normfHs=(1 ??), for s ≥0.
Now, we state our results as follows.
Theorem 1 Let u0∈L2∩L3(R3) with divu0= 0 and θ0∈L2∩L3(R3). Suppose that(u(t,x),θ(t,x))is a weak solution to the equations(1.1). If the partial derivative of the pressure π satisfies
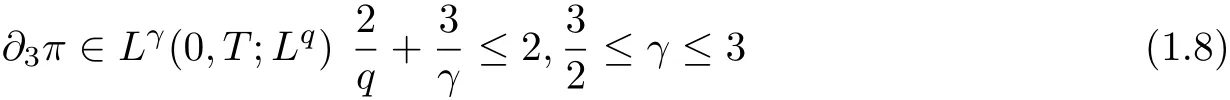
then the weak solution (u,θ) is regular on (0,T].
Remark 1 It is easy to see that (1.8) on the partial derivative of pressure does not seem comparable with(1.7),at least there is no inclusion relation between them. On the other hand,thanks to the fact that Boussinesq equations (1.1) with θ = 0 reduces to the Navier-Stokes equations (1.2), Theorem (1) covers the previous results on the Navier-Stokes equations.
Next, in order to derive the criteria on regularity of weak solutions to the Boussinesq fluid equations (1.1), we introduce the definition of a weak solution.Definition 1 Let u0(x)∈L2σ(R3)and θ0(x)∈L2(R3). A measurable function(u(x,t),θ(x,t))is called a weak solution to the Boussinesq equations (1.1) on [0,T] if(a)

and
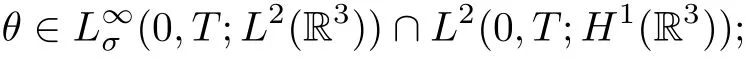
(b) (u,θ) verifies (1.1) in sense of distribution, i.e., for any test function φ ∈C∞0(R3×[0,T])with ?·φ=0, for any scalar function and ? ∈C∞0(R3×[0,T]), and for almost every t ∈[0,T],we have
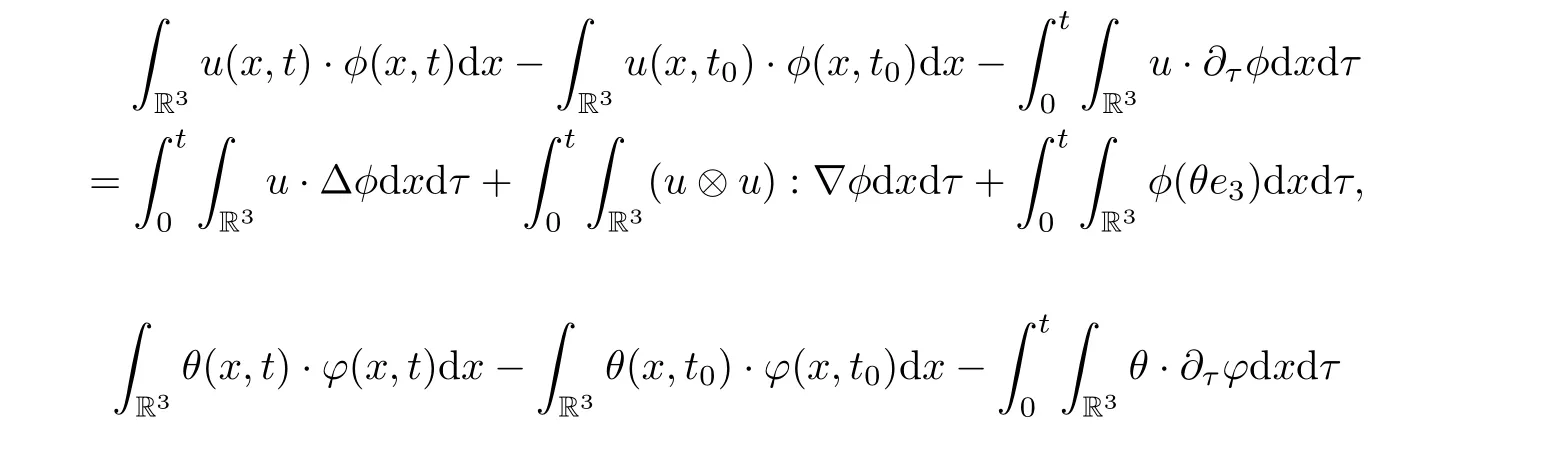
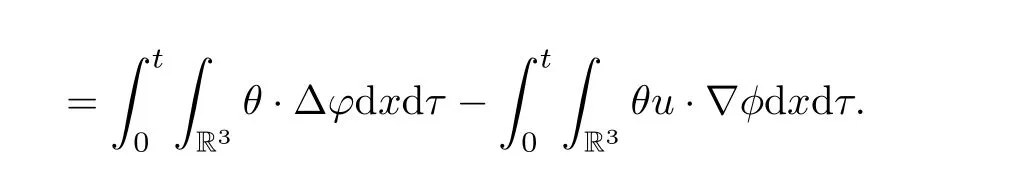
(c) For any scalar function η ∈C∞0(R3)) and for almost every t ∈[0,T]
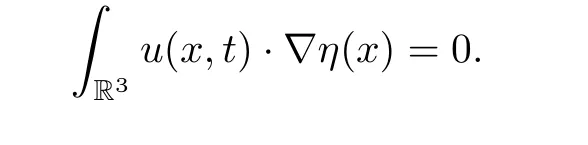
For convenience, we will use the following elementary inequalities(see [1] for details).
Lemma 1 Let q,λ,α,β ∈R satisfy
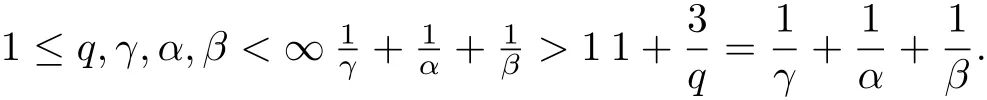
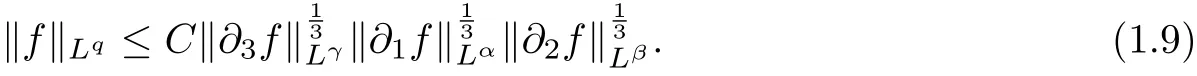
Lemma 2 (Serrin’s uniqueness theorem in [13])
Let u0∈(L2(Rd))dwith ?·u0=0. Assume that there exists a solution u the Navier-Stokes equations on (0,T)×Rd(for some T ∈(0,+∞])with initial value u0so that:
1)u ∈L∞((0,T);(L2(Rd))d);
2)u ∈L2((0,T);( ˙H1(Rd))d);
3)For some q ∈(d,∞],u ∈Lp((0,T);(Lq(Rd))d),with
Then u is the unique Leray solution associated with u0on (0,T).
The plan of the paper is arranged as follows. We first state some preliminary and some important inequalities on functional settings and then prove Theorem 1 in Section 2.
§2. Proof of Theorem 1
The proof of Theorem 1 is divided into two steps.
Taking the inner product of |θ|p?2θ with the second equation of (1.1), by integrating by parts and using the incompressibility condition, we have

where we have used
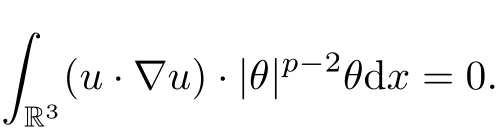
For ?t ∈[0,T],?p ∈[1,+∞], by integrating in time,

Next, taking the inner product of u with the first equation of (1.1), we have after integration by parts,
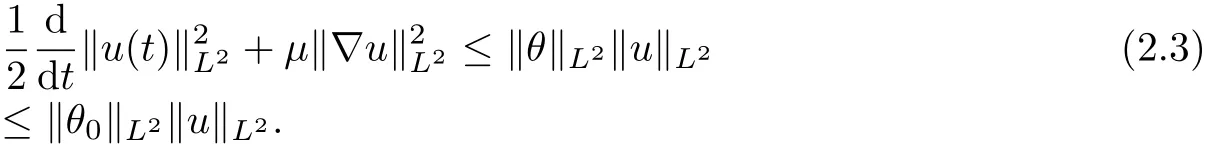
therefore, it follows from Gronwall inequality that
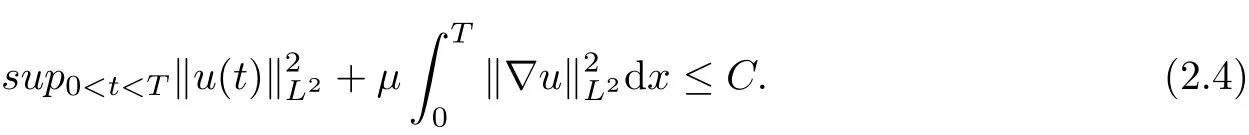
Firstly, taking the inner product of |u|u with the first equation of (1.1), it can be deduced that
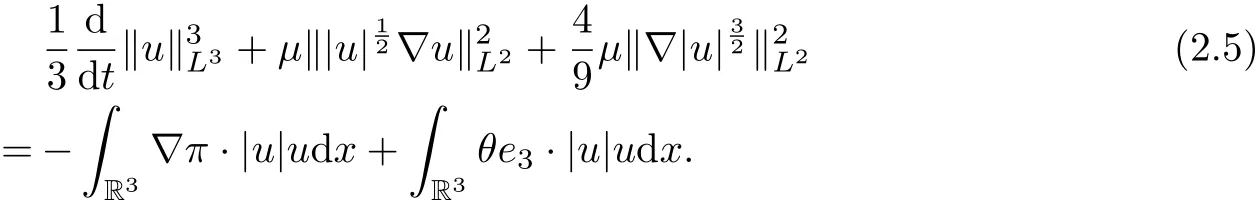
where we have used the following facts:
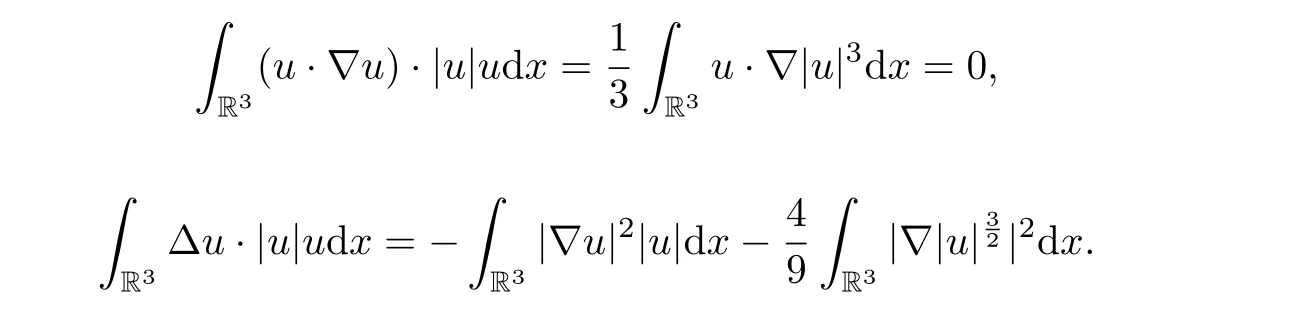
Next, taking the inner product of |ω|ω with the second equation of (1.1), it follows that
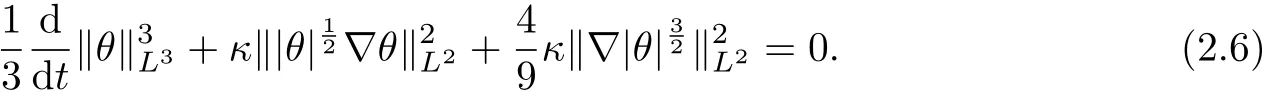
where we have used the following facts:Summing (2.5) and (2.6), we get
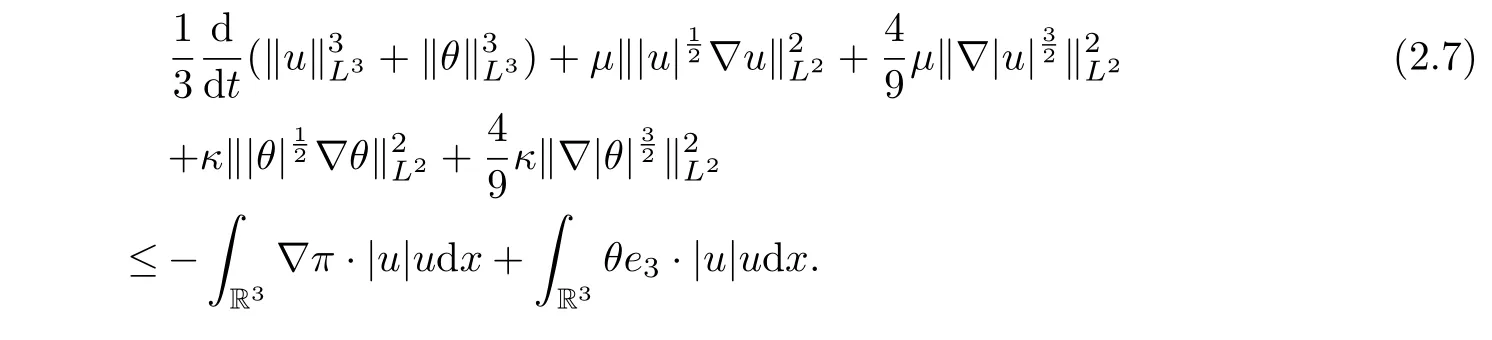
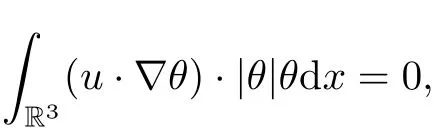
Employing the H¨older and Young inequalities and integration by parts, we derive the estimation of the first term on the right-hand side of (2.7) as
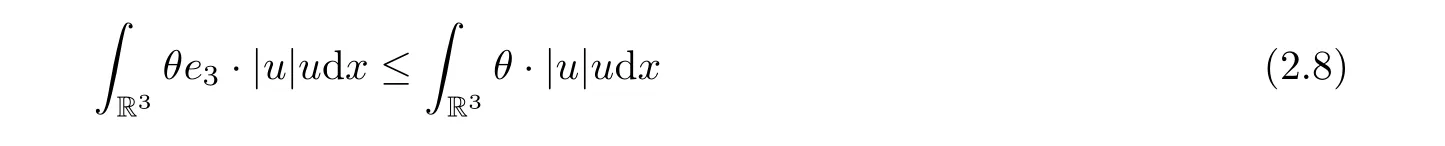
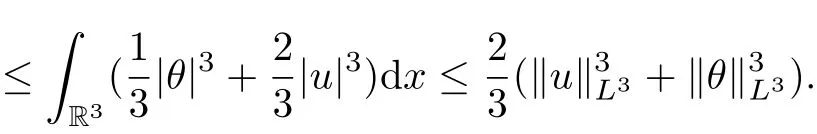
Inserting (2.8) into (2.7), we obtain
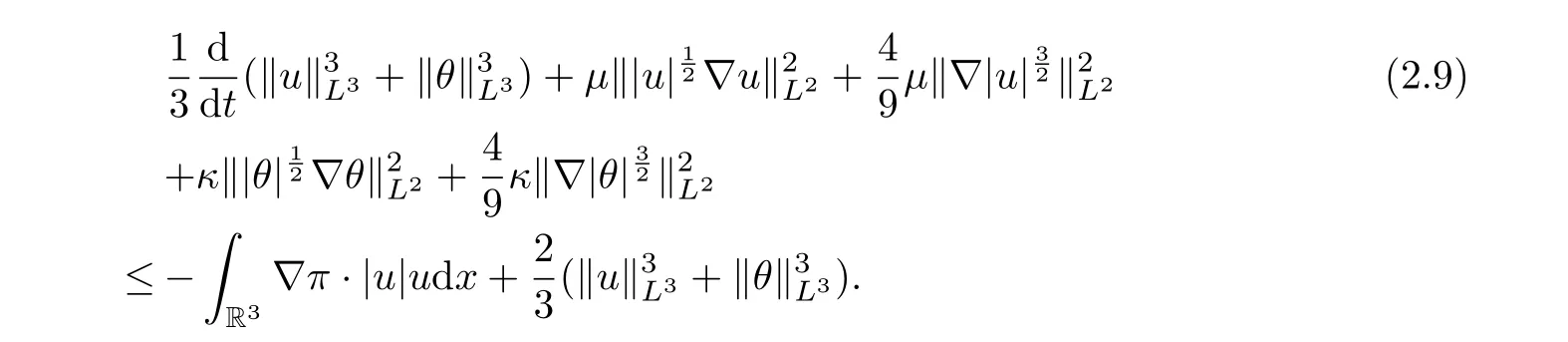
Denote

In order to estimate I, we need apply the operator ?div on both sides of the first equation of(1.1) gives
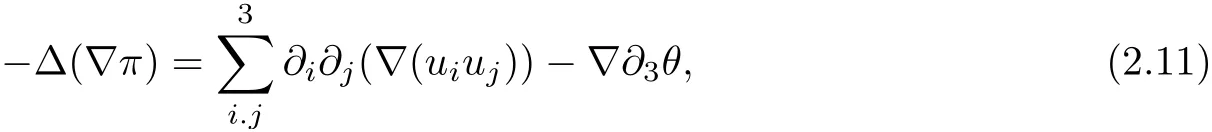
therefore, according to Calderon-Zygmund inequality in R3, for all 0 By integrating by parts and the H¨older inequality yield that for I By the inequality (2.12), H¨older and Gagliardo-Nirenberg inequalities,?πLαcan be estimated as follows α3?1 41?|u|32L522?α3?uL2+C. Together with (2.19) and (2.14) give Inserting (2.16)into (2.9), we find Then, by means of Gronwall inequality , we have Together with energy inequality (2.4) and the condition (1.8) implies that From (2.19) and the Serrin’s uniqueness theorem (2), we can chose p = 3andq = 9, then the weak solution (u,θ) is regular on (0,T). Therefore, by the standard regularity arguments of weak solutions, we complete the proof of Theorem 1.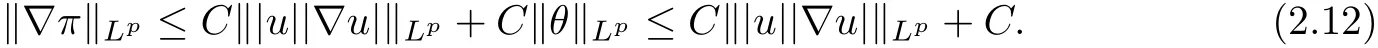
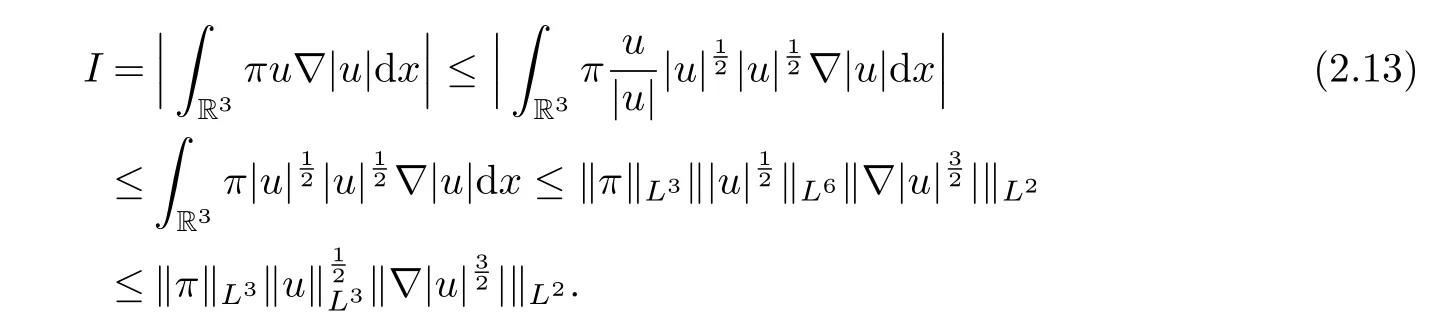
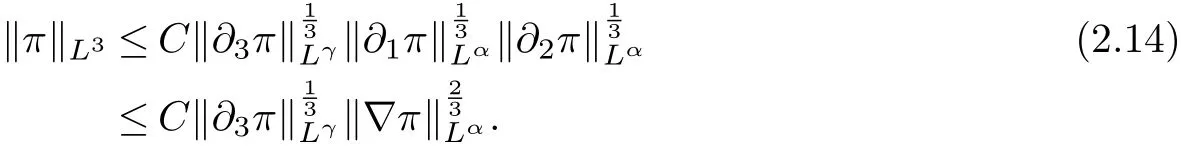
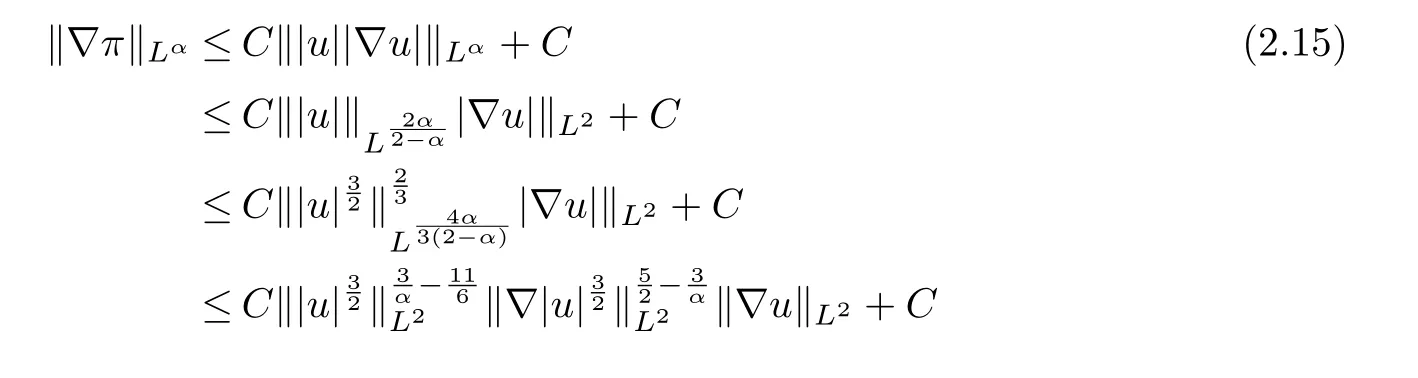
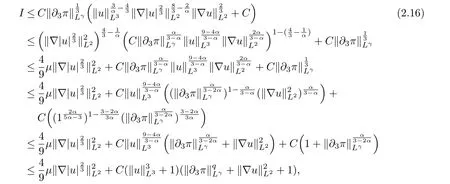
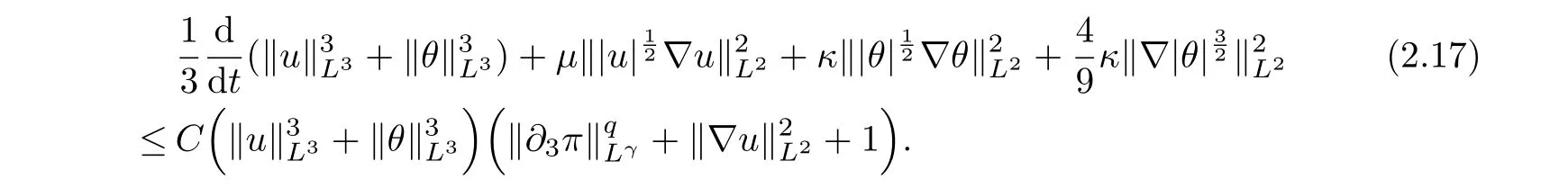
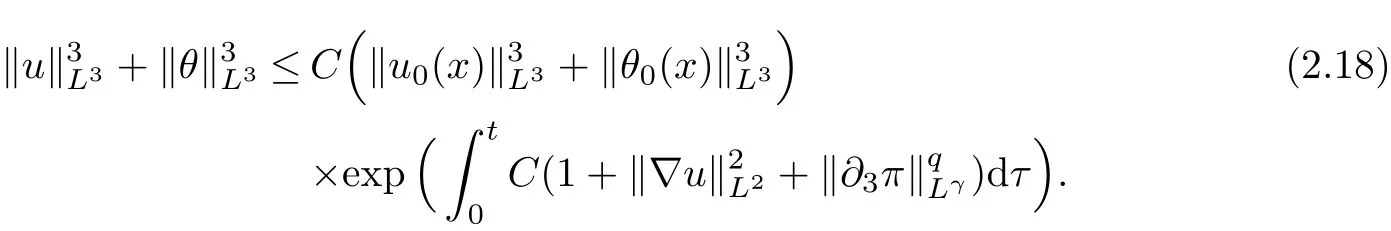
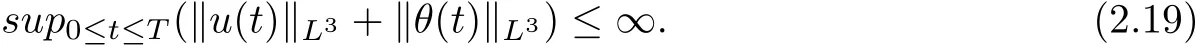
 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- Multimodal Learning Using Haar Scattering Transform
- On the Solution of Fermat-type Differential-difference Equations
- Fixed-time Consensus for Leader-follower Second-order Multi-agent Systems
- Triple Positive Solutions for a Third-order Three-point Boundary Value Problem
- Globally Bounded Solutions in A Chemotaxis Model of Quasilinear Parabolic Type
- Finite Difference Methods for the Time Fractional Advection-diffusion Equation
