Triple Positive Solutions for a Third-order Three-point Boundary Value Problem
WU Hong-ping
(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, P.R.China)
Abstract: In this paper, we study the existence of triple positive solutions for the nonlinear third-order three-point boundary value problemwhere η ∈[0, )is a constant, by using a fixed-point theorem due to Avery and Peterson, we establish results of triple positive solutions to the boundary value problem, and an example is given to illustrate the importance of result obtained.
Key words: Third-order three-point boundary value problem; Positive solutions; Fixedpoint theorem
§1. Introduction
Third-order differential equations arise in a variety of different areas of applied mathematics and physics. In recent years, the existence and positive solutions for nonlinear third-order ordinary differential equations with a three-point boundary value problem have been studied by several authors. For example, Agarwal[1], Anderson[2], Ma[3], Guo[4], Palamides[5], Sun[6],for more existence results see[7-10].

In [5], Palamides et.al considered the following boundary value problem (BVP)and found a Green’s function, although this Green’s function is not positive, the obtained solutions is still positive and increasing.
In this paper, we investigate the existence of triple positive solutions for the nonlinear third-order three-point boundary value problem
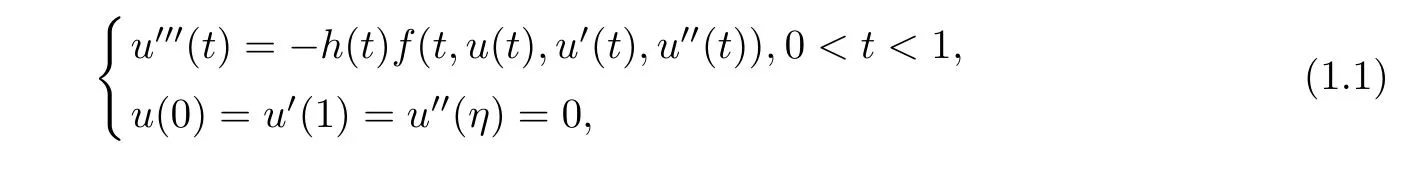
In the rest of paper, we make the assumptions:

§2. Preliminaries and Lemmas
Definition 2.1Let E be a Banach space over R, a nonempty convex closed set K ?E is said to be a cone provided that
i) au ∈K for all u ∈K and a>0;
ii) u,?u ∈K implies u=0.
Definition 2.2Suppose K is a cone in a Banach space E, the map ψ said to be a nonnegative continuous concave functional on K provided that ψ : K →[0,∞) is continuous and

Similarly we say the map ? is nonnegative continuous convex functional on K provided that ?:K →[0,∞)is continuous and

Definition 2.3Suppose K is a cone, let α a nonnegative continuous concave functional on K, γ and β be nonnegative continuous convex functional on K , and ? a nonnegative continuous functional on K. For positive real number a,b,c,d, we defined the following convex sets:

and a closed set

Consider the Bananch space C[0,1] equipped with the standard normand let

Lemma 2.1[5]The BVP

admits the unique solution u(t)=, where G(t,s) is Green’s function.

Further, for s ≥η

for s ≤η

Thus we obtain

also

Consequently

Lemma 2.2[5]Let y ∈K0, then the BVP

admits the unique solution u(t)=which is monotonic.
Remark 2.1From the proof of Lemma 2.2[5],we know the solution of BVP(2.4)satisfiesit is show that u(t) strictly increasing and convex for t ∈[0,η] , and concave for t ∈[η,1].
Lemma 2.3[5]For any y ∈K0, the unique solution u(t) of (2.4) also belongs to the cone K0and furthermore it satisfiesis arbitrary.
Theorem 2.1[11]Let E be a Banach space, K ?E be a cone in E. Let γ and β are nonnegative continuous convex functionals on K, α is a nonnegative continuous concave functionals on K,and ? is a nonnegative continuous functionals on K satisfying ?(λx)≤λ?(x)for λ ∈[0,1], such that for some positive numbers M and d

(C1) {x ∈P(γ,β,α,b,c,d)|α(x)>and α(Tx)>b for x ∈P(γ,β,α,b,c,d);
(C2) α(Tx)>b for x ∈P(γ,α,b,d) with β(Tx)>b;
Then T has at least three fixed points x1,x2,x3∈such that γ(xi)≤d for i=1,2,3; b<α(x1); a
§3. Main Result
Define

Note that for u ∈K, we have
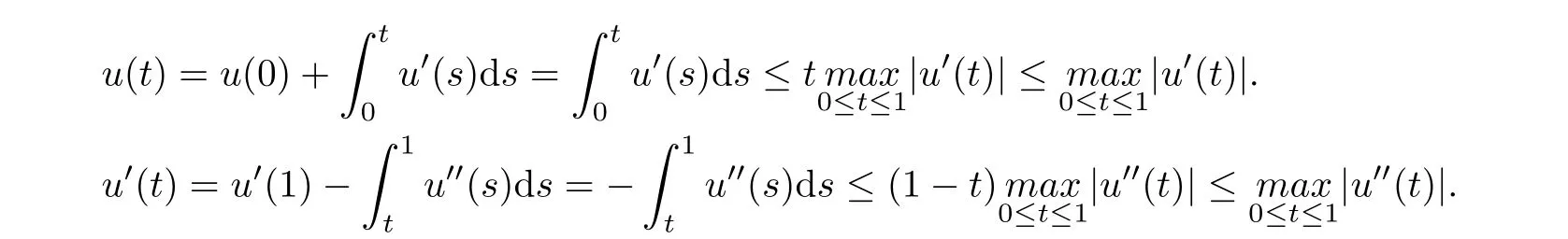
Therefore

Define functionals

Then α,β,γ,?:K →[0,∞) are nonnegative continuous functionals , α is concave and β,γ are convex. Consequently, we have

Define the integral operator T :K →C[0,1] by

Lemma 3.1[5]T :K →K is completely continuous.
For convenience, we denote the constants by

Theorem 3.1 Suppose (H1)-(H2) hold, assume there exist 0 < a < b < θ?d such that the following condition hold
then the BVP(1.1) has at least three positive solutions u1,u2and u3, satisfying

Proof We now show that all the conditions of Theorem 2.1 are satisfied.
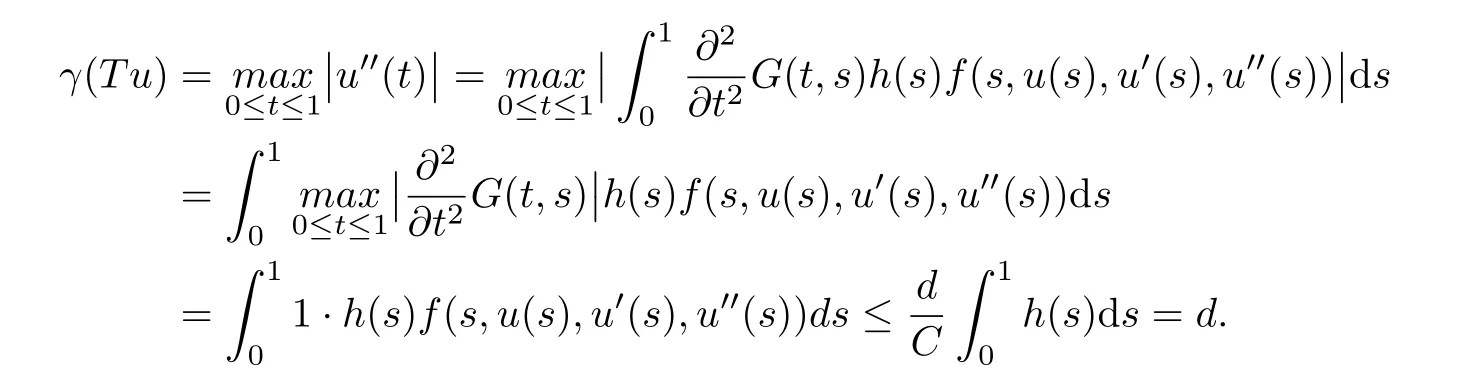
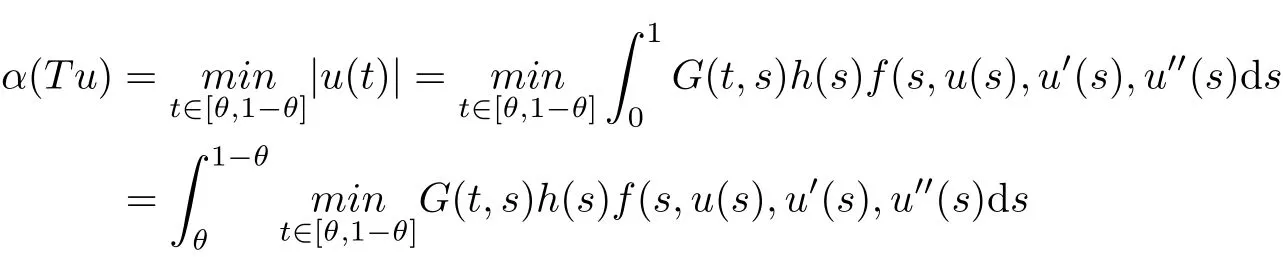

i.e. α(Tu) > b for all u ∈P(γ,β,α,b,d). This show that condition (C1) of Theorem 2.1 is satisfied.
Secondly, from (3.2) we have
α(Tu) ≥θ?β(Tu) ≥= b for all u ∈P(γ,α,b,d) with β(Tu) >Thus condition(C2) of Theorem 2.1 is satisfied.
Finally, we check out condition (C3) of Theorem 2.1 hold too.
Clearly, as ?(0)=0 So condition(C3)of Theorem 2.1 is also satisfied. Therefore,an application of Theorem 2.1 implies there exist three positive solutions of BVP(1.1), such that In addition, β(u1) We present an example to check out our results. Consider the BVP Then all assumptions of Theorem 3.1 hold. Thus,BVP(4.1)has at least three positive solutions u1,u2,u3, and

§4. Example
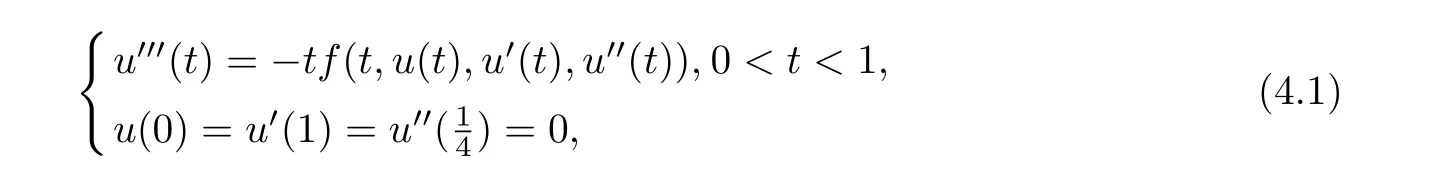

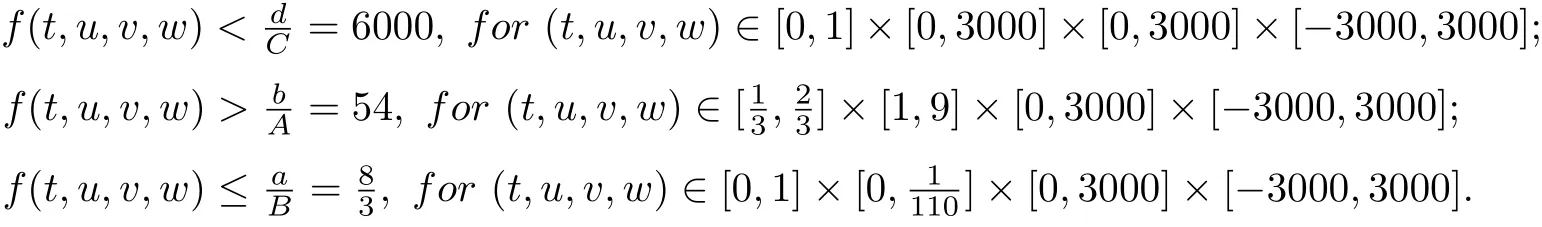

 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
