A New NTRU-Type Public-Key Cryptosystem over the Binary Field
Youyu Gu, Xiongwei Xie and Chunsheng Gu
Abstract: As the development of cloud computing and the convenience of wireless sensor netowrks, smart devices are widely used in daily life, but the security issues of the smart devices have not been well resolved.In this paper, we present a new NTRU-type public-key cryptosystem over the binary field.Specifically, the security of our scheme relies on the computational intractability of an unbalanced sparse polynomial ratio problem (DUSPR).Through theoretical analysis, we prove the correctness of our proposed cryptosystem.Furthermore, we implement our scheme using the NTL library, and conduct a group of experiments to evaluate the capabilities and consuming time of encryption and decryption.Our experiments result demonstrates that the NTRU-type public-key cryptosystem over the binary field is relatively practical and effective.
Keywords: Public key cryptosystem, NTRU, lattice attack, meet in the middle attack.
1 Introduction
In the past few years, cloud computing has attracted a lot of research efforts.At the same time, more and more companies start to move their data and operations to public or private clouds.For example, out of 572 business and technology executives that were surveyed in Berman et al.[Berman, Lynn, Marshall et al.(2012)],51% relied on cloud computing for business model innovation.These demands also become a driving force for the development of cloud security and wireless security, which ranges from very theoretical efforts such as homomorphic encryption to very engineering mechanisms defending against side channel attacks through memory and cache sharing [Xie and Wang (2013b); Xie, Wang and Qin (2015); Pan, Lei, Zhang et al.(2018)].
As the development of cloud computing and the convenience of wireless sensor netowrks, smart devices are widely used in daily life, such as smart phones, but the security issues of the smart devices have not been well resolved [Xie and Wang (2013a); Ren, Shen, Liu et al.(2016)].One reason is that smart devices do not have enough computing resource, and they are not suitable for the use of traditional cryptographic schemes directly, such as RSA,ECC.Therefore, in order to design a lightweight cryptographic scheme suitable for smart devices, this paper constructs a candidate public key encryption scheme based on NTRU over the binary field to partially solve the security problems in smart device applications.The NTRU public-key cryptosystem was introduced by Hoffstein, Pipher and Silverman in 1996 [Hoffstein, Pipher and Silverman (1998)].Unlike more classical public-key cryptosystems such as RSA, ECC or ElGamal, its security is based on the hardness of finding the shortest vector problem (SVP) and the closest vector problem (CVP) in a cyclic modular lattice, which are not known to be susceptible to quantum attack.As a consequence, it is considered as one of the most viable quantum-resistant public-key cryptosystems, whereas the classical cryptosystems based on the hardness of integer factorization, or the discrete logarithm over finite fields are no longer secure once the quantum computer becomes a reality[Shor(1997)].
The NTRU system is determined by a set of parameters(n,q,p,χf,χg,χr,χe).First,the parameter n is set to be prime and used to define the polynomial ring R = ?[x]/〈xn-1〉.Second,p and q are relatively prime,q is much larger than p,and they are used to define the quotient polynomial rings Rq=R/qR and Rp=R/pR that form the ciphertext space and message space of NTRU,respectively.Finally,(χf,χg,χr,χe)are probability distributions defined in certain subsets of R,and output random polynomials with most coefficients being 0 and the rest in the set{1,-1}.
Given these parameters of NTRU, Alice samples g from χg, and f from χfso that f is invertible in Rqand Rp.Alice publishes h = g/f ∈Rqas his public key, and keep f as his private key.To encrypt a message polynomial m ∈Rp,Bob takes Alice's public key h,samples r from χrand e from χe,computes the ciphertext c = p(hr+e)+m ∈Rq,and sends it to Alice.To decrypt the ciphertext c,Alice computes a=fc mod q,and outputs the message polynomialmod p.
Related work.Since NTRU is the most efficient lattice-based public-key cryptosystem,many variants of NTRU were presented by replacing the ring of integers ? with other rings.Gaborit, Ohler, and Solé introduced CTRU as an analogue to NTRU where the coefficients of polynomials are frominstead of ?.However,Kouzmenko[Kouzmenko(2006)] presented a polynomial time algorithm which breaks CTRU.This is because the CTRU system uses low-degree polynomials instead of "small norm" polynomials.As a consequence, the CTRU system is no longer secure.Several variants of NTRU are proposed by using the Dedekind domains, including GNTRU over the Gaussian integers?[i][Kouzmenko(2006)],ETRU over the Eisenstein integers ?[ζ3][Nevins,Karimianpour and Miri (2010); Jarvis and Nevins (2015)], NTRUSIGN [Hoffstein, Howgrave-Graham,Pipher et al.(2003)]and NTRU Signature Scheme(NSS)[Hoffstein,Pipher and Silverman(2001)].The security of these variants is equivalent to the security of NTRU in general.On the other hand, some non-commutative versions of NTRU are also described over the non-commutative ring, including MaTRU over integer matrices [Coglianese and Goi(2005)], QTRU and BQTRU over quaternion algebras [Malekian, Zakerolhosseini and Mashatan(2009,2011);Bagheri,Sadeghi and Panario(2017)].
Recently, Aggarwal et al.[Aggarwal, Joux, Prakash et al.(2017)] presented a new public-key cryptosystem via Mersenne numbers (AJPS) that is an integer version of the NTRU system.The security of the AJPS system relies on the conjectured hardness of the Mersenne low hamming ratio assumption.However, Beunardeau et al.[Beunardeau,Connolly,Géraud et al.(2017)]described a practical LLL-based algorithm that recovering the secret key from the public key is much faster than the security estimates in Aggarwal et al.[Aggarwal,Joux,Prakash et al.(2017)].Furthermore,de Boer et al.[de Boer,Ducas,Jeffery et al.(2017)]further refined the attack analysis of Beunardeau et al.[Beunardeau,Connolly,Géraud et al.(2017)].
Although there are many research results related to variants of NTRU in the past few years,secure NTRU-type public key cryptosystem over the binary field has not attracted a lot of research afforts.
1.1 Our contribution
We propose a new NTRU-type public key cryptosystem over the binary field.As a warmup,Alice chooses two sparse polynomials f,g ∈R2=?2[x]/〈xn+1〉,and sets f as the secret key and h = g/f ∈R2as the public key.For encrypting a bit b ∈{0,1}, Bob chooses sparse polynomials r,e,generates a ciphertext c=rh+e+bm,where m is the polynomial of all coefficients 1, and sends c to Alice.For decryption, Alice computes a = cf and outputs b=0 if the number of the non-zero coefficients of a is less than a fixed value(e.g.,n/4),otherwise b=1.The advantage of this scheme is simple,but it can not be extended to multi-bit schemes easily.In this paper,we propose a multi-bit scheme by using unbalanced sparse polynomials.Namely,Alice chooses two sparse polynomials f,g ∈R2so that the degree of f is at most β, and sets the public keyand the secret key f,where β,θ are positive integers and β +θ <n.It is not difficult to construct a multi-bit scheme by using these unbalanced sparse polynomials.Concrete construction is described in Section 2.However,the use of unbalanced polynomials in the construction makes it more vulnerable to man-in-the-middle attacks.Therefore,we will take large enough parameters to resist this attack.
Furthermore,we observe that the distribution of coefficients“1”in the product of two sparse polynomials is almost uniform.If the number of coefficients “1” in the product of two sparse polynomials is k,the probability that each coefficient is“1”is approximately equal to k/n.As a consequence, we assume that this distribution is uniform to improve the efficiency of our scheme.
1.2 Organization
The remainder of the paper is organized as follows.Firstly,we propose a NTRU-type public key cryptosystem and theoretically prove the correctness of it in Section 2.In Section 3,we analyze the security of our scheme and discuss the resistance to popular known attacks.In Section 4, we implement our NTRU-type scheme,and evaluate the capabilities and the consuming time for encryption and decryption.Finally,Section 5 concludes the paper.
2 NTRU-type public key cryptosystem
In this section,we present the details of our new NTRU-type public key cryptosystem over the binary field.Our construction is similar in form to the variant of NTRU [Stehlé and Steinfeld (2011)].However, our scheme works over the binary field ?2, and their variant works over ?qwith q ?2.It is not trivial to generalize their construction from ?qto ?2.For simplicity,we concretely define the notations of our scheme as follows:
λ: the security parameter.
ρ=λ/4: the number of coefficients"1"of random polynomials.
α=4ρ: the length of message vectors.
δ =2ρ: the extended length of plaintext bits.
β =4ρ2: the degree of secret key polynomials.
n ≥20ρ2+1: the degree of modulo polynomial defined the ring.
R=?2[x]/〈xn+1〉: the working polynomial ring.
R?: the set of all invertible polynomials in R.
P =?2[x]: the ring of sampling random polynomials.
P<β: the set of all polynomials of degree less than β in P.
m ?1: the tensor product of two vectors m and 1.
2.1 Construction
Key generation:(pk,sk)←KeyGen(1λ).
(1)Choose a prime n ≥20ρ2+1 so that
GCD(xn+1,x2β+1)=x+1 mod 2,xn+1=(x+1)k(x) mod 2,
where k(x)has at most two irreducible factors modulo 2.
(4)Output the public key pk ={λ,ρ,n,β,h},and the secret key sk ={s}.
Encryption:(c)←Enc(pk,m).
(1)Given the public key pk,and a plaintext vector m ∈{0,1}α,compute d = m ?1,and set
c=rh+e+d mod (xn+1) mod 2
(3)Output the ciphertext c.
Decryption:m ←Dec(sk,c).
(1)Given the secret key sk,and a ciphertext c,compute over R
w =fc mod (xn+1) mod 2
v =w mod (x2β+1) mod 2
(2)For i=0,1,··· ,α-1
(2.2)If ui≥ρ,then mi=1,otherwise mi=0.
(3)Output the plaintext vector m.
Remark 2.1(1)To improve the efficiency of our construction,we can relax the condition of the factor number of xn+1 over the polynomial ring P.Namely,for a large enough prime n,the factor number of x is only required to be a small constant.In this case,in addition to factor x+1 of xn+1,other factors need to be able to resist man-in-the-middle attacks.
(2) Our scheme uses unbalanced sparse polynomials to encrypt multi-bit plaintexts.If we construct a single-bit scheme, we only require to use sparse polynomials instead of unbalanced sparse polynomials.
2.2 Correctness
For the correctness of our scheme, it requires to prove that the algorithm Dec correctly recovers the plaintext from a ciphertext with high probability.
We first give the following Chernoff bound.
Lemma 2.2Let X1,··· ,Xδbe independent identically distributed random variables such that Xi←Berτ,where Berτdenotes the Bernoulli distribution with the parameter 0 ≤τ ≤1.Ifthen
Pr[X ≥(τ +?)δ]≤e-2δ?2.
Lemma 2.3Given sk and a ciphertext c,the algorithm Dec correctly decrypts the plaintext vector m.
Proof.According to Dec,we have
w =fc mod (xn+1) mod 2=f(rh+e+d) mod (xn+1) mod 2=rg+fe+fd mod (xn+1) mod 2
By KeyGen,we have deg(f)=deg(s(x2β+1)+1)<3β =12ρ2.
Again through deg(d)≤2β-1 <8ρ2,we get deg(fd)<20ρ2<n.
So,the polynomial fd remains unchanged in modulo xn+1.Namely,fd mod xn+1=fd.
Without loss of generality, let e = e(1)+x2βe(2).Similarly, the polynomial fe(1)also remains unchanged in modulo xn+1 since deg(e(1))≤2β-1.
So,w =u+fe(1)+fd mod 2,where u=(rg+fx2βe(2)) mod (xn+1).
As a result,v =w =(u mod (x2β+1))+e(1)+d mod (x2β+1) mod 2.
In the following analysis, we assume that the coefficients "1" of noise polynomials are uniformly distributed.Concretely speaking, the probability that any coefficient of a noise polynomial y with length k is"1"is equal to
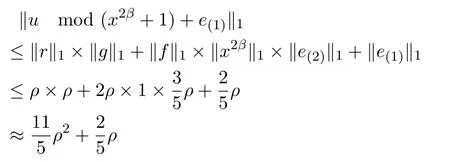
Since z = u mod (x2β+1)+e(1)is a noise polynomial in v, the probability that any coeffciient of z is"1"is equal to
Therefore,the expected number of"1"in a polynomial of length 2ρ is
By Lemma 2.2,we have
So,the probability that mican be correctly recovered is about
3 Security
In this section, we will define decisional unbalanced sparse polynomial ratio problem(DUSPR)and the DUSPR assumption,and analyze some known attacks.
The security of the NTRU variant [Stehlé and Steinfeld (2011)] is reduced to worst-case problems over ideal lattices, but the security of NTRU is still based on the computational hardness assumption generated by NTRU.Similarly,the security of our NTRU-type scheme is also based on the new DUSPR hardness assumption.
3.1 Hardness assumption
Definition 3.1 Decisional unbalanced sparse polynomial ratio problem (DUSPR).
Given the above parameters{λ,ρ,β,n},a distinguisher D is said to(λ,ρ,β,n,t,?)-solve the DUSPRλ,ρ,β,nproblem if
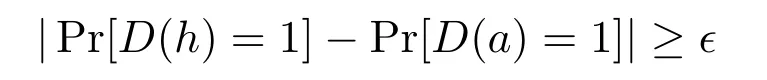
where h=g/f ∈R?,f =s(x2β+1)+1,g ←,s ←with s,g ∈R?,and a ←R?,and D runs in time at most t.
Our public key cryptosystem is based on the following assumption.
Definition 3.2 DUSPR assumption.For any probabilistic distinguisher D that(λ,ρ,β,n,t,?)-solves the DUSPRλ,ρ,β,nproblem for all large enough λ, where ρ = λ/4,β =4ρ2,n=20ρ2+1,and t is polynomial in λ,the advantage ? that D holds is negligible as a function of λ.
Lemma 3.3Under the DUSPR assumption, the public key encryption scheme(Enc,Dec)described in Section 2 is secure against chosen plaintext attack.
Proof.Given two polynomials d0,d1∈P<2βcorresponding to plaintext vectors m0,m1,for i=0,1 let ci=rih+ei+dimod (xn+1) mod 2,be the ciphertexts of di,where
Note that for simplicity we assume that c1,c2∈R?.The reason is that if GCD(ci,xn+1)1,we can flip the 0-th coefficient of ci.
By contradiction,assume that there exists a polynomial time algorithm B,so that
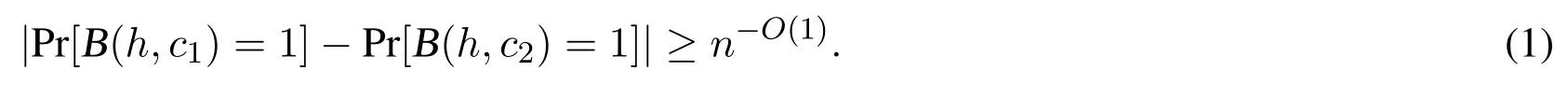
Let b ←R?.According to the DUSPR assumption,for any polynomial time algorithm A we have
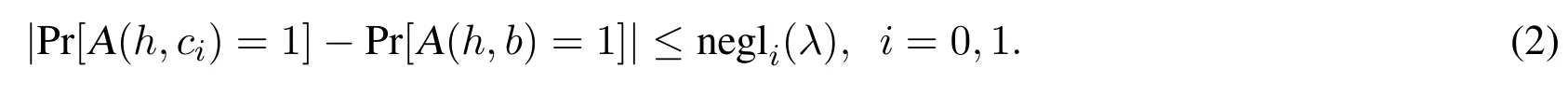

Table 1: The concrete parameter settings of our NTRU-type scheme
Since B is a polynomial time algorithm,we get
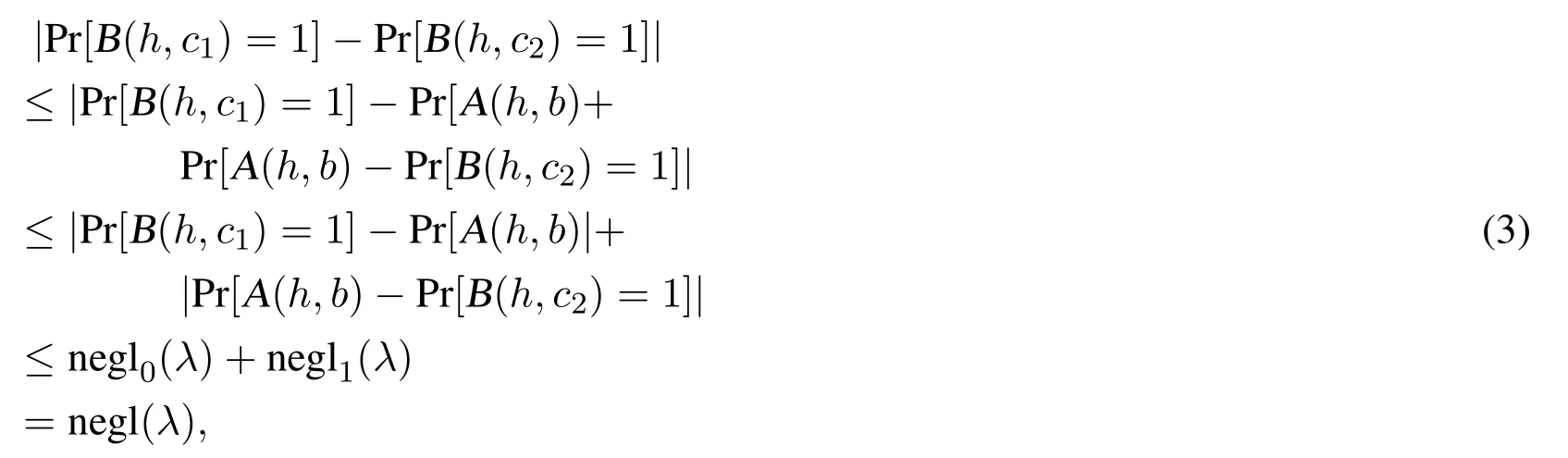
where negl0(λ),negl1(λ),and negl(λ)are negligible functions in λ.
This generates a contradiction for the expression(1)and(3).
3.2 Known attacks
In the following subsection, we theoretically analyze how our proposed scheme prevents known attacks, including NTRU-type lattice attack, meet in the middle attack, and attack of factoring modulo xn+1.Our analysis result demonstrates that our scheme can resist all these known attacks.
NTRU-type lattice attack.For the NTRU system, given the public key h = g/f over the ring ?q[x]/(xn-1),it is easy to construct the NTRU public lattice[Coppersmith and Shamir(1997);Hoffstein,Pipher and Silverman(1998)]as follows:

where H is a circulant matrix generated from h.
According to the parameter settings of NTRU,the vector(g,f)in L1has size(df+dg)1/2,where df,dgare the number of the non-zero coefficients of f,g, respectively.Since det(L1) = qn, the Gaussian heuristic suggests that(g,f)is in general the shortest vector in L1.However,the current lattice reduction algorithm that find(g,f)requires exponential in the security parameter n.
Similarly,for our NTRU-type system,given the public key h = g/f over ?2[x]/(xn+1),we can also construct a lattice from h.Owing to using the unbalanced private key f, we only need to use the 2β rows of the circulant matrix H generated by h.The reaseon is thatfh=(s+1)h+s(x2βh)=f1h+f2h.As a reasult,we write a matrix form as follows:

Table 2: The performance of our NTRU-type scheme

where H is a circulant matrix generated from h, H[i : j]represents the sub-matrix of the i-th row to the j-th row of H.
By our parameter settings,the vector(g,f1,f2)in L2has size(3ρ+1)1/2or(3ρ-1)1/2.Since det(L2) = 2n,the Gaussian heuristic suggests that(g,f1,f2)is usually the shortest vector in L2.When n is large enough, the lattice reduction algorithm that computes(g,f1,f2)requires time complexity at about 2O(n).
Meet in the middle attack.The idea of the meet-in-the-middle attack on NTRU[Howgrave-Graham (2007)] is that if f1+ f2= f, then (f1+ f2)h = g mod q.In other words, the entries of y1= f1h and y2= -f2h differ only by 0 or 1 mod q.According to this property,the meet-in-the-middle attack performs sampling f1with df/2"1" coefficients, and storing them in boxes dependent on the y1.If two binary elements f1,f2are satisfied f =f1+f2,then we hope that this can be detected by a collision in a box.For any collisions, we can retrieve the f1,f2from the stored box, and determine whether(f1+f2)h is binary or not.Once we find a very small vector in the NTRU public lattice,it is very likely one of the rotation of(g,f).According to the analysis,the classical(resp.quantum)meet-in-the-middle attack requires the time complexity and space complexity at least[Howgrave-Graham (2007)] (resp.[de Boer,Ducas,Jeffery and Wolf(2017)]).
Similarly, for our NTRU-type system, it is not difficult to verify that the classical (resp.quantum)meet-in-the-middle attack requires the time complexity and space complexity at least
Attack of factoring xn+1 modulo 2.According to our parameter settings,the xn+1 has at most three factors modulo 2.In other words, xn+1 = (x+1)k(x) mod 2 such that k(x) is irreducible or k(x) = k1(x)k2(x) modulo 2.As far as we know, when n is large enough,no effective algorithm can use the factors of xn+1 to attack our system.
4 Implementation
To evaluate the encryption and decryption capabilities of the proposed approach,and access its consuming time on different security level,we conduct one group of experiments.The experiment environment setup is as follows.We implemented our NTRU-type public key cryptosystem over the NTL library.All programs were run on the physical machine,which has a 3.20 GHz Intel Core i5-3470 processor,and 8 GB of RAM.
Tab.1 is our concrete parameter settings.We define different security level with different parameter values.Tab.2 is the performance result of our NTRU-type scheme.Note that the estimate of the security level mainly relies upon the time complexity of the classical meet-in-the-middle attack on our NTRU-type scheme.
When security level is 80 (λ=120, ρ=30, β=3600, n=18013), we have 100% successful rate for testing frequency=2000,and average excryption/decryption time is about 3 ms with 150 expansion rate.When security level is 160 (λ=200, ρ=50, β=10000, n=50021), we have 100%successful rate for testing frequency=2000,and average excryption/decryption time is about 15ms with 250 expansion rate.From our experiments result, we can notice that if we directly encrypt plaintexts by applying our public key scheme,its performance is relatively weak,especially for the ciphertext expansion rate.However,if we use our public key scheme for key encapsulation mechanism, our scheme will be relatively practical and effective.
It should be noted that we did not optimize our implementation and only illustrate the relative practicality of our construction.
5 Conclusions
In this paper,we propose a new NTRU-type public-key cryptosystem over the binary field,whose security relies on the computational intractability on the DUSPR problem.We present the details of our new NTRU-type plublic key cryptosystem with the theoretical analysis,and prove our decryption algorithm correctly recovers the plaintext from a ciphertext with high probability.We also theoretically analyze and prove that our proposed cryptosystem could avoid known attacks,including NTRU-type lattice attack,meet in the middle attack,and and attack of factoring modulo xn+1.Furthermore,we implement our scheme using the NTL library,and conduct a group of experiments in different security level.Our result demonstrates that our proposed NTRU-type public-key cryptosystem over ?2is relatively practical.
Immediate extensions to our approach consist of the following aspects.First, we plan to experiment our approach with cell phone so that we can evaluate its improvements comparing to traditional cryptosystem.Second, we plan to study the feasibility and security of digital signature and authentication through conducting NTRU-type public key cryptosystem over the binary field.Finally, we plan to reduce the security of our scheme to the learning parity with noise(LPN)[Pietrzak(2012)]problem theoretically,so that we could get rid of the assumption of DUSPR.
Acknowledgement:This work was supported by the National Natural Science Foundation of China (Nos.61672270, 61702236 and 61602216) and Changzhou Sci&Tech Program(Grant No.CJ20179027).We thank anonymous reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Conflict of Interest
We declare that the funding in the Acknowledgment section did not lead to any conflict of interests regarding the publication of this manuscript.Also,there is no any other conflict of interests in the manuscript.
 Computers Materials&Continua2019年7期
Computers Materials&Continua2019年7期
- Computers Materials&Continua的其它文章
- A Cross-Tenant RBAC Model for Collaborative Cloud Services
- Outage Capacity Analysis for Cognitive Non-Orthogonal Multiple Access Downlink Transmissions Systems in the Presence of Channel Estimation Error
- Knowledge Composition and Its Influence on New Product Development Performance in the Big Data Environment
- Fuzzy Search for Multiple Chinese Keywords in Cloud Environment
- A Novel Broadband Microstrip Antenna Based on Operation of Multi-Resonant Modes
- Network Embedding-Based Anomalous Density Searching for Multi-Group Collaborative Fraudsters Detection in Social Media
