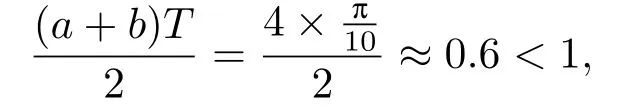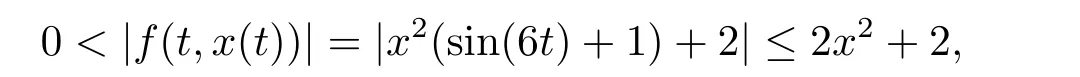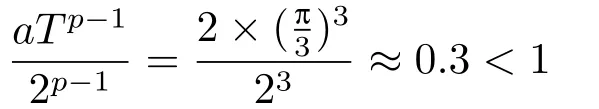一類廣義Linard方程周期正解的存在性
崔笑笑,程志波,姚紹文
( 河南理工大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,河南 焦作454000)
1.引言

作為一個簡化模型出現(xiàn)在科學(xué)和工程的許多領(lǐng)域,由于它可以用來模擬振蕩電路或者簡單的鐘擺運(yùn)動,在20世紀(jì)上半葉,人們對它進(jìn)行了深入的研究.例如,Van der Pol 振蕩器

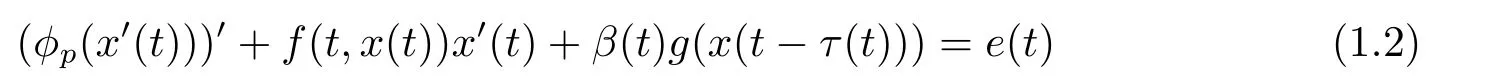
的周期解的存在性,其中自治函數(shù)g(x)滿足半線性條件
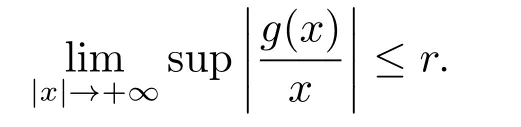

證明了方程(1.3)存在一個周期解.

其中?p(s)=|s|p?2s,p ≥2是常數(shù),f,g ∈C(R×R,R)是關(guān)于第一個變量t的T-周期函數(shù),e(t)∈C(R,R)是一個T-周期函數(shù).利用Mansevich-Mawhin連續(xù)定理,我們給出了下面的結(jié)論.
定理1.1假設(shè)下列條件成立:
(H1) 存在正常數(shù)a和b,使得對一切(t,x)∈[0,T]×R,有0<|f(t,x)|≤a|x|p?2+b;
(H2) 存在正常數(shù)D,使得對一切(t,x)∈[0,T]×(D,+∞),有g(shù)(t,x)?e(t)<0,并且對一切(t,x)∈[0,T]×(?∞,0],有g(shù)(t,x)?e(t)>0.則方程(1.4)在下列一種條件下至少有一個T-周期正解,
(I)p=2,且
(II)p>2,且
注1.1本文與文[4]有很大的不同.方程(1.2) 中自治函數(shù)g(x)滿足半線性條件,而方程(1.4)中非自治函數(shù)g(t,x)僅僅只需要滿足條件(H2),這也就是說,g可以滿足次線性條件,半線性條件和超線性條件.因此本文的結(jié)論改進(jìn)和擴(kuò)展了文[4]的結(jié)論.
注1.2與方程(1.3)相比,方程(1.4)中的摩擦系數(shù)由f(x)變?yōu)榱薴(t,x),摩擦項(xiàng)的積分在估計方程周期解的先驗(yàn)界時難度大大增加,所以文[7]中的方法不再適用,這就要求我們需要尋找其他方法克服這一困難.在這里還需要特別說明的是,當(dāng)f(t,x(t))≡f(x(t))時,方程(1.4)轉(zhuǎn)化成了方程(1.3),文[7]是本文的一個特例.
作為定理1.1的應(yīng)用,我們能得到下面的推論.
推論1.1假設(shè)條件(H2)成立,方程(1.3)至少有一個T-周期正解.
注1.3本文證明的是方程(1.4)周期正解的存在性,而文[4,7]中僅僅證明的是周期解的存在性,因此本文是對文[4,7]進(jìn)一步的深入研究.
隨后,我們研究方程(1.1)周期解的全局漸近穩(wěn)定性.設(shè)
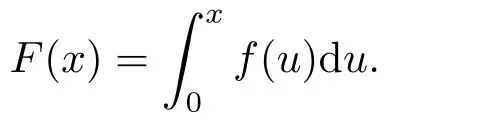
定理1.2假設(shè)f(0)=0,g(0)=0成立,更進(jìn)一步假設(shè)下列條件成立:
(H3) 存在正常數(shù)D1,D2,使得對一切x ∈(?∞,?D1),有g(shù)(x)<0,并且對一切x ∈(D2,+∞),有g(shù)(x)>0;
(H4) 存在正常數(shù)c和d,使得對一切x ∈R,有|g(x)|≤c|x|+d;
(H5) 對一切x ∈R,有g(shù)(x)≥x;
(H6) 對一切x ∈R,有xF(x)>0.則如果方程(1.1)有唯一全局漸近穩(wěn)定的周期解x?(t)=0.
2.主要結(jié)論
首先考慮方程(1.4)的同倫方程
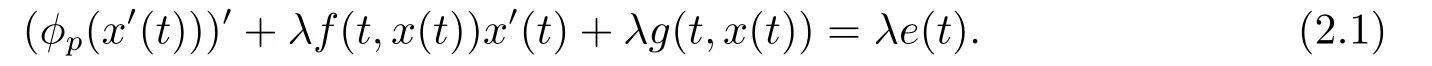
為了方便表示,我們定義

引理2.1假設(shè)存在常數(shù)E1,E2使得下列條件成立:
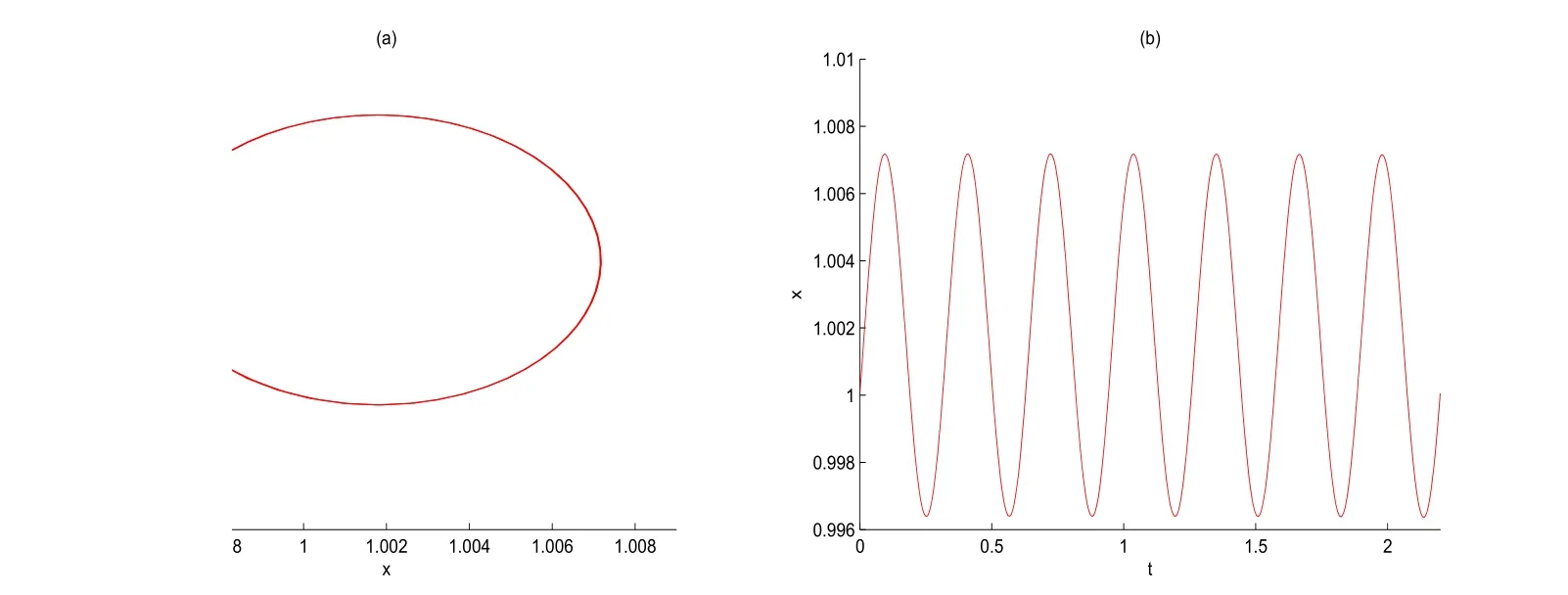
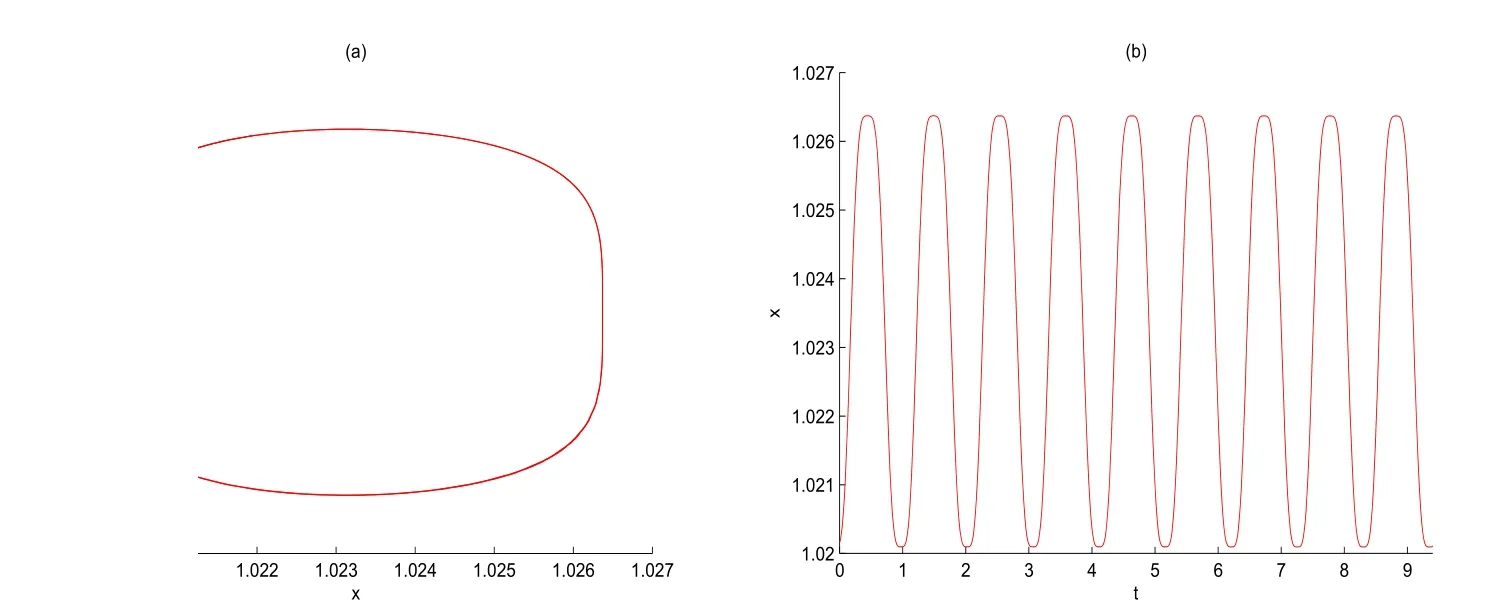
(i)對于方程(2.1)的每一個解x(t)都有∥x∥ (ii)對于方程 的每一個解C都滿足|C| (iii) 則方程(1.4)至少有一個T-周期解. 接下來,我們證明方程(1.4)至少有一個T-周期正解. 對定理1.1的證明首先,我們斷言方程(2.1)的所有可能的解都是有界的.令x(t)∈C1T是方程(2.1)的任意一個T-周期解. 我們斷言存在ξ ∈[0,T],使得 則 令t3,t4∈(0,T)分別是?p(x′(t))的極大值點(diǎn),極小值點(diǎn),則 且 那么 把t3代入方程(2.1)得 因?yàn)??p(x′(t3)))′=0,方程(2.3)化為 由條件(H1) 可知f(t,x)不變號,不妨設(shè)f(t3,x(t3))>0,又x′(t3)≥0,由方程(2.4), 由條件(H2),我們可得 同理可得 (i)若x(t3)∈(0,D),令ξ=t3,則|x(ξ)| (ii)若x(t3)∈[D,+∞),由方程(2.5) 及x(t) 關(guān)于t的連續(xù)性,存在常數(shù)ξ且x(ξ)∈[x(t4),x(t3)],使得|x(ξ)|=D.這就證明了方程(2.2).接著我們有 并且 結(jié)合上面兩個不等式,我們得到 對方程(2.1)左右兩邊同時乘以x(t)并且在[0,T]上積分,我們得到 設(shè)G1:={x ≤0,t ∈R},G2:={0< x ≤D,t ∈R},G3:={x > D,t ∈R},則方程(2.8)可化為 由條件(H2),我們有 則方程(2.9)可化為 下面介紹一個經(jīng)典的不等式,存在只依賴于p的常數(shù)k(p)>0 使得 接下來,我們考慮下面的兩種情況. (I) 若p=2,則q=2,把p=2,q=2代入方程(2.13)可得 (II) 若p >2,則由方程(2.13) 很容易地看出當(dāng)時,有界,同(I),存在常數(shù)使得 由方程(2.6)和方程(2.16)可得 令M1=max{M11,M12},則 因?yàn)閤(0)=x(T),所以存在一點(diǎn)t5∈(0,T)使得 則我們可得 事實(shí)上,假設(shè)x′(t)無界,那么一定存在正常數(shù)M′′2,使得對某些x′(t)有∥x′∥>M′′2成立,那么我們有∥?p(x′)∥=∥x′∥p?1≥(M′′2)p?1,這與方程(2.18)矛盾,所以方程(2.19)成立. 令E1>M1,E2>M2為常數(shù),從方程(2.17)和方程(2.19)能得到對于方程(2.1)的每一個解x(t)都有 所以引理2.1的條件(i)成立. 由條件(H2),對于方程 的每一個解C都滿足 所以引理2.1的條件(ii)成立. 從方程(2.15)我們知道E1>D,?E1<0.所以從條件(H2)我們能得到 所以引理2.1的條件(iii)成立. 假設(shè)x(t)是方程(1.4)的一個T-周期解,令是x(t)在[0,T]上的最小值點(diǎn),那么 并且我們能得到 由條件(H2),有 因此對一切t ∈R,有 這說明方程(1.4)至少有一個T-周期正解. 定義3.1如果x?(t)是方程(1.1)的一個周期解,x(t)是方程(1.1)的任意一個解并且滿足 那我們稱x?(t)是全局漸進(jìn)穩(wěn)定的. 對定理1.2的證明步1 考慮方程(1.1)周期解的存在性. 首先對方程(1.1)的同倫方程 兩邊同時在[0,T]上積分并化簡得 由積分中值定理,存在一點(diǎn)η ∈(0,T)使得 由條件(H3)可知, 令D?=max{D1,D2},則 由方程(2.6)可得 對方程(3.1)左右兩邊同時乘以x(t)并且在[0,T]上積分并化簡可得 由條件(H4),方程(3.3)化為 余下對周期解x?(t)的存在性證明與定理1.1的證明過程類似,此處省略. 步2 考慮方程(1.1)的周期解x?(t)是全局漸近穩(wěn)定的. 方程(1.1)可轉(zhuǎn)化為方程組 其中 由f(0)=0,g(0)=0 可知x?(t)=0 是方程(1.1)唯一的周期解,即x?(t)=(0,0)T是系統(tǒng)(3.5)唯一的周期解,設(shè)x(t)=(x1(t),x2(t))T是系統(tǒng)(3.5)的任意一個解.對系統(tǒng)(3.5),我們選擇形如下式的李雅普諾夫函數(shù), 由條件(H5)和(H6),V(x1,x2)沿著系統(tǒng)(3.5)軌線的全導(dǎo)數(shù)為 由Barbalat 引理[16]可知, 即 自此定理1.2得證. 接下來,通過例子,相圖和時間序列圖來闡明我們的定理. 例4.1考慮下面的二階廣義Linard方程 對比方程(4.1)和方程(1.4)可知,f(t,x(t))=e?|x|sin(20t)+3,并且滿足 即滿足條件(H1),其中 取D=2,可以得到 即滿足條件(H2).接下來我們驗(yàn)證條件 圖4.1 -周期解對應(yīng)的相圖及時間序列圖: (a)初始值為(1,0.103331)的-周期解的相圖; (b)-周期解的時間序列圖 成立.因此,通過定理2.1可得方程(4.1)至少有一個-周期正解. 例4.2考慮下面的p-Laplacian廣義Linard方程 這里我們?nèi)=4.對比方程(4.2)和方程(1.4)可知,f(t,x(t))=x2(sin(6t)+1)+2,并且滿足 即滿足條件(H1),其中a=2,b=2.g(t,x(t))=?x3(cos(6t)+2)+2,e(t)=cos(6t), 取D=2,可以得到 即滿足條件(H2).接下來我們驗(yàn)證條件 圖4.2 -周期解對應(yīng)的相圖及時間序列圖: (a)初始值為(1.0236,0.04985)的 -周期解的相圖; (b)-周期解的時間序列圖


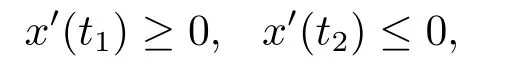
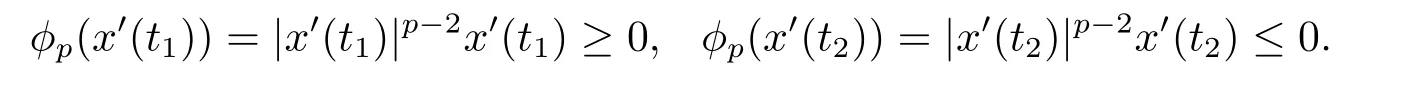
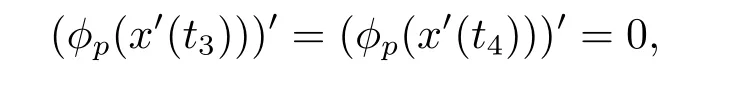


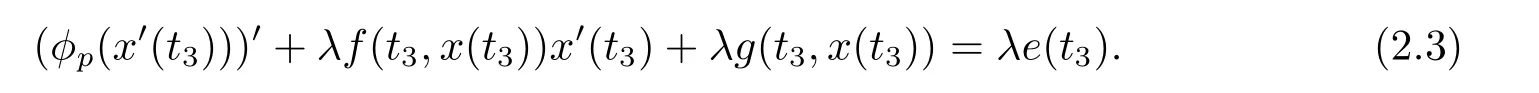

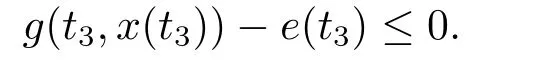
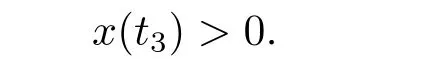
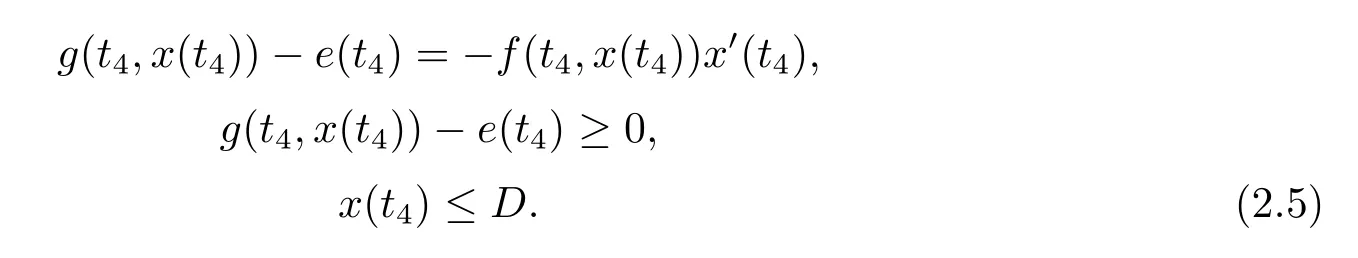
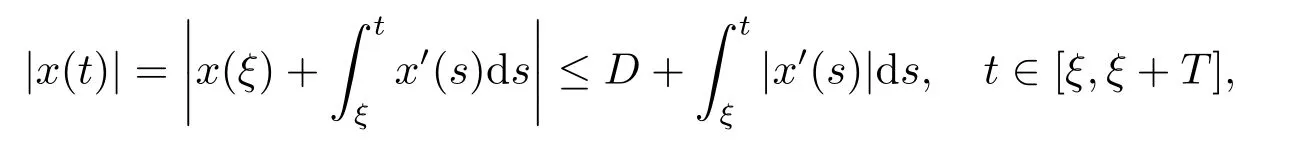
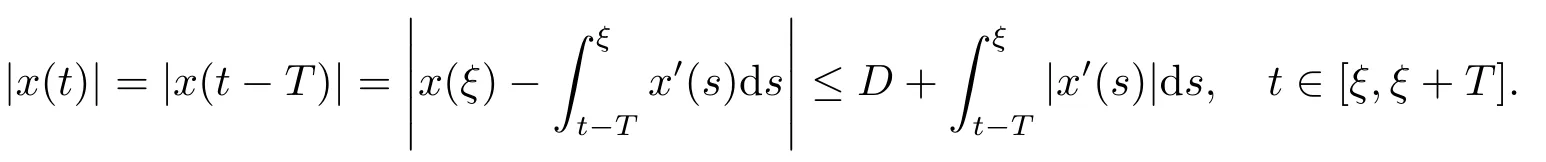
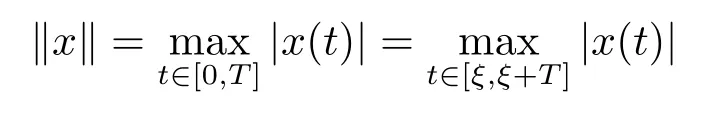
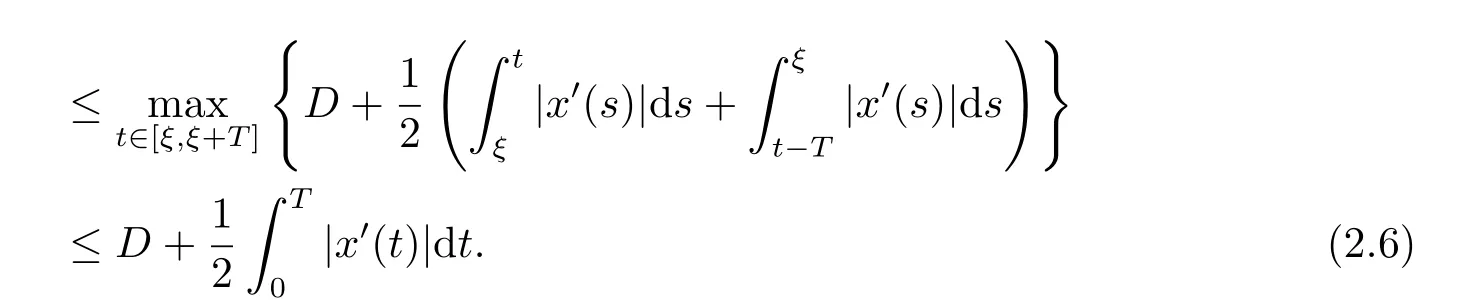


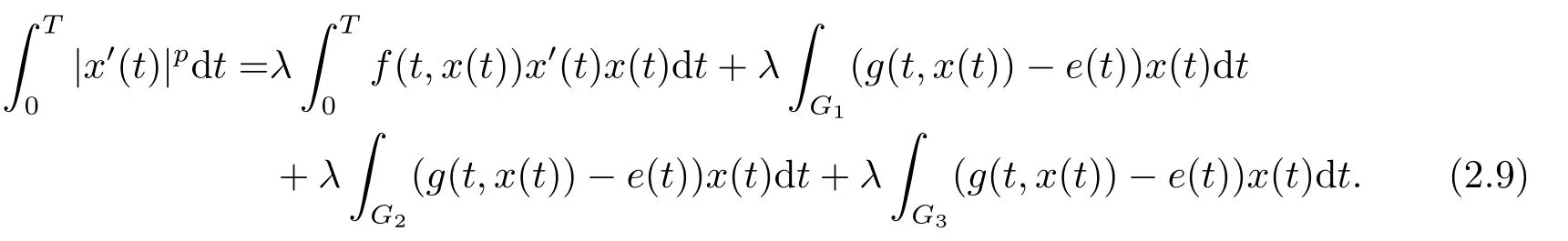


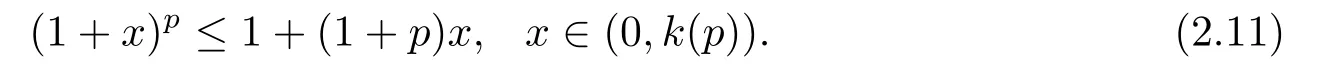
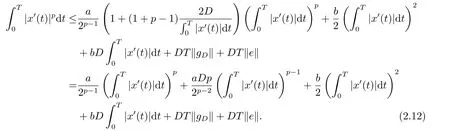
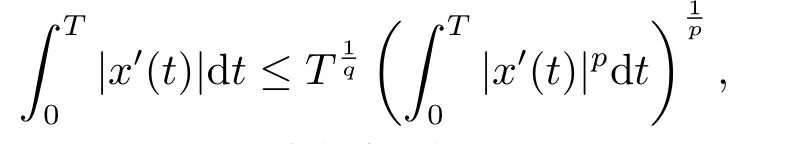



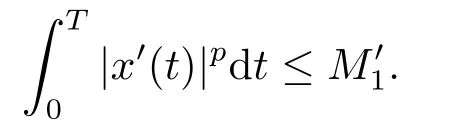
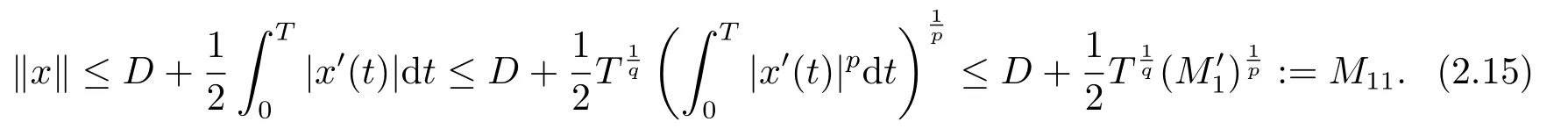

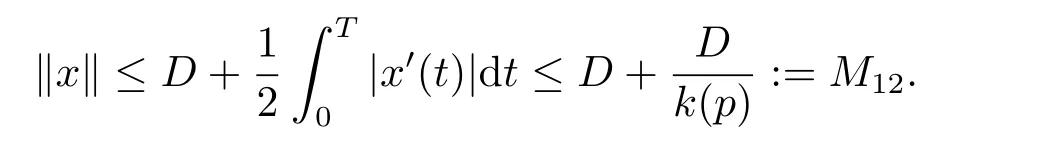

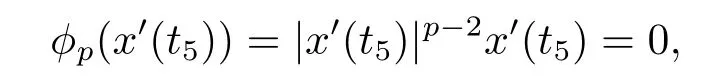
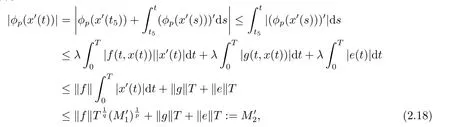

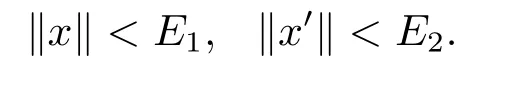
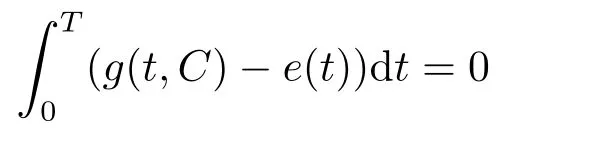




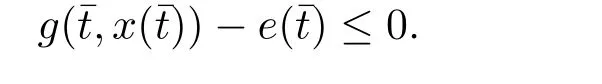

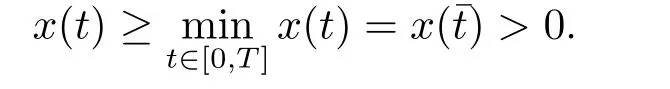
3.周期解的漸近穩(wěn)定性

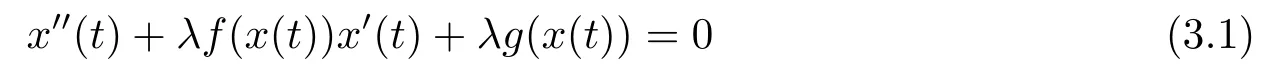
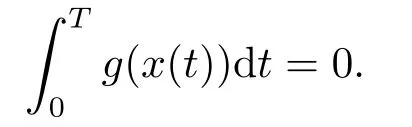


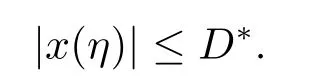
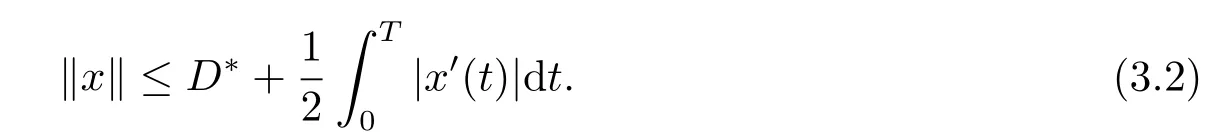
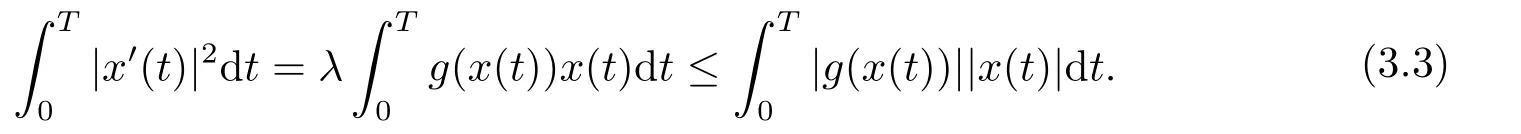
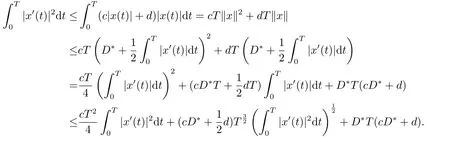

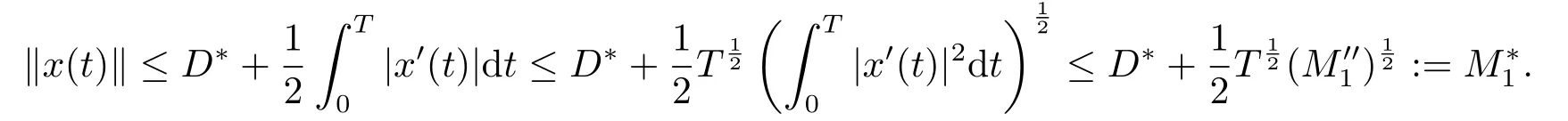

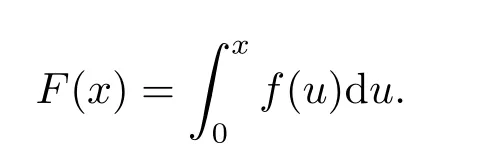
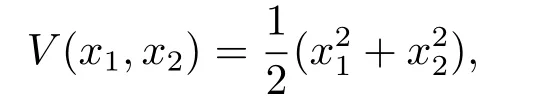
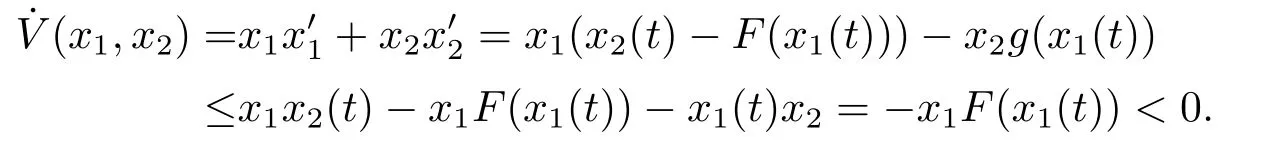
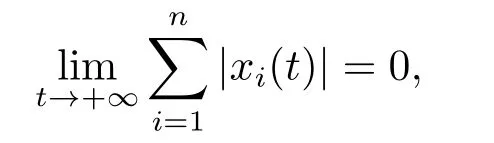

4.例子