統(tǒng)計遭遇數(shù)學的尷尬

中國科學技術大學統(tǒng)計與金融系 蘇 淳 (郵編：230026)

2018年高校招生全國統(tǒng)一考試理科數(shù)學試卷I的第20題是一道關于產(chǎn)品檢驗的題目.題目開宗明義, 面對的是大批量的產(chǎn)品. 產(chǎn)品成箱包裝, 每箱200件. 每箱先抽檢20件,根據(jù)檢驗結果決定是否對余下的所有產(chǎn)品作檢驗. 命題者怕在這里引起誤會, 不可謂不仔細地斟酌了詞句, 特別強調(diào)了要決定的是“是否對余下的所有產(chǎn)品作檢驗”, 說明這里的選項只有兩個: 要么對余下的所有產(chǎn)品都作檢驗(全檢), 要么就都不檢驗(全不檢), 不存在部分檢驗的問題.正是在這種思路的指導之下, 誕生了對于第(2)小題(ii)的官方解答.

站在統(tǒng)計學的角度來看, 這種解答是沒有問題的. 因為它考慮的是實際需求. 要檢驗的是大批量的產(chǎn)品, 不僅僅是一箱, 而是許多許多箱. 所以只需對“全檢”與“全不檢”的費用作一比較, 以決定是否需要全檢.

問題尷尬的是, 它是出在“數(shù)學試卷”中的題目, 而且它自身又帶有明顯的“數(shù)學特點”, 這就讓人難以弄清它到底是要考“統(tǒng)計”, 還是要考“數(shù)學”了.

題目中的第(1)小題要求學生用極大似然估計估計出產(chǎn)品的不合格率, 沒有出現(xiàn)“極大似然估計”這個統(tǒng)計學上的名詞, 完全用的是數(shù)學語言, 求函數(shù)的極大值點. 學生理所當然地把它作為數(shù)學題來做, 求導數(shù), 求導函數(shù)的零點, 觀察導函數(shù)的符號, 確認p0=0.1就是函數(shù)f(p)的最大值點.

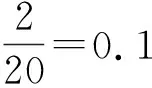
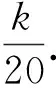
既然這里是考數(shù)學, 那么一以貫之, 通題就應當都按數(shù)學問題處理. 至少別人按數(shù)學問題做了, 不能算錯.例如, 有人這樣解答第(2)小題(ii):

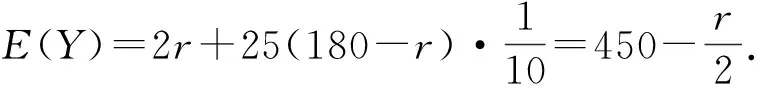
在r=180時,E(Y)達到最小. 所以應對剩下的產(chǎn)品“全檢”.

這種求最小值的處理方式與第(1)小題的精神一致. 都是用數(shù)學中的最值作為問題的解答. 既然(i)中可用最值點作為不合格率的估計, 那么(ii)中也可以按最值的標準取舍檢驗方案.

更何況, 這里還涉及到邏輯中的如何否定“全稱命題”的問題. 無論怎么說, 對“全檢”的否定是“不全檢”,包括“部分檢”與“全不檢”. 正如不少中學教師指出的, 這是中學數(shù)學教學中反復強調(diào)的, 而且也是作為高考所要考核的內(nèi)容的. 不能在同一張卷子中體現(xiàn)不同的要求.

事實上, 第(2)小題(ii)的官方解答中所采用的取舍標準只有具備產(chǎn)品檢驗經(jīng)驗的人才知道, 因為只有面對在大批量產(chǎn)品時,才會只在“全檢”與“全不檢”之間進行選擇.

在我國的本科專業(yè)分類中已經(jīng)把統(tǒng)計學獨立出來, 作為與數(shù)學并列的一級學科, 就是因為“統(tǒng)計不是數(shù)學”.數(shù)學的一個基本特征是:“一個問題只有一個答案”, 統(tǒng)計學則不然, 對同一個問題, 可以有不同的答案. 例如前面說到的, 對同一個參數(shù), 可以用頻數(shù)估計, 也可以用極大似然估計, 它們往往會有所不同. 在當前大數(shù)據(jù)時髦的今天,面對同樣的數(shù)據(jù), 得出不同結論的情況就更為常見.

中學里既然把統(tǒng)計放到數(shù)學中來學, 那就有一個如何教如何學如何考核的問題. 尤其是在出高考題時, 更需要考慮周全. 前些年我在參與出高考數(shù)學安徽卷時, 一直把握一條原則, 就是大題盡量考概率. 因為概率是數(shù)學, 一是一, 二是二,不會遭遇尷尬. 統(tǒng)計則不然, 需要謹慎而又謹慎.