Calibration and performance of two different constitutive models for rockfill materials

*

aInstitute of Applied Mechanics,Graz University of Technology,Graz 8010,Austria

bChangjiang Institute of Survey,Planning,Design and Research,Wuhan 430010,China

cCollege of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China

Calibration and performance of two different constitutive models for rockfill materials

Lin-ke Lia,Zhan-jun Wangb,Si-hong Liuc,Erich Bauera,*

aInstitute of Applied Mechanics,Graz University of Technology,Graz 8010,Austria

bChangjiang Institute of Survey,Planning,Design and Research,Wuhan 430010,China

cCollege of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China

Available online 15 November 2016

In this paper,two different concepts for the constitutive modeling of the mechanical behavior of creep-sensitive rockfill materials are presented.Specif i cally,the performance of an extended generalized plasticity model proposed by Wang is compared with a simplified version of the hypoplastic constitutive model for weathered rockfill materials proposed by Bauer.Both models can ref l ect the inf l uence of the mean stress on the incremental stiffness,the peak friction angle,and the dilatancy angle.The so-called solid hardness def i ned for a continuum description and originally introduced by Bauer is embedded in both models.Hydrochemical,thermal,and mechanical weathering are usually caused by environmental changes and are taken into account in a phenomenological description with an irreversible and time-dependent degradation of the solid hardness.A degradation of the solid hardness is usually accompanied by creep deformation of the stressed rockfill material.It is shown that appropriate modeling of creep deformation requires at least a unified description of the interaction between the time-dependent process of degradation of the solid hardness and the stress state.In this context,the solid hardness can be understood as a key parameter for describing the evolution of the state of weathering of the rockfill material.Particular attention is also paid to the necessary procedure for determining the constitutive constants of the two different constitutive models.Finally,the performance of the two different constitutive models is demonstrated by comparing the results obtained from numerical simulations with experimental data from the creep-sensitive rockfill material.

Rockfill material;Creep;Generalized plasticity;Hypoplasticity;Constitutive model

1.Introduction

The adaptation of the parameters of a constitutive model to experimental data is called calibration,and from a mathematical point of view it is an inverse problem.The existence and uniqueness of a solution are of fundamental importance to the practical application of a material model.For more sophisticated constitutive models,a higher number of parameters are usually involved in the constitutive equations in a nonlinear manner.Without knowledge of the physical scope of the values of the parameters,the application of standard optimization procedures can fail.Therefore,the formulation of appropriate functions for the calibration procedure plays an important role(e.g.,Bauer,1996).The type and number of experiments necessary for calibration can also be determined according to the calibration equation derived from the constitutive model.It is worth noting that the application of a particular material model is not independent of the question as to whether the experiments necessary for the calibration can be carried out.This is not only a question of the equipment of the laboratory,but also a question of uncertainties of specimensampling,the pre-compaction of the material at the construction site,f i nancial aspects,and time can play a role as well.For a more ref i ned constitutive modeling of microstructure effects,the task of calibration can be rather complex and the number of necessary experiments is usually much higher than for simple material models.If suff i cient data are not available,some parameters have to be estimated or a simplified constitutive model has to be used instead.In order to evaluate the performance and physical limitation of a material model under consideration,the values of the constitutive parameters obtained should also be controlled by comparing the results of the numerical simulation of element tests with the corresponding laboratory experiments and,if available, with data from field tests.

The present paper focuses on constitutive modeling and calibration of coarse-grained and weathered rockfill materials, which can show pronounced density,pressure,and ratedependent mechanical properties.In particular,weathered and soft rockfill materials can exhibit pronounced creep deformations,which can be explained by the process of progressive weathering accompanied by grain crushing and plastif i cation of interparticle contacts of the stressed rockfill material(Alonso and Cardoso,2010).As a consequence of the degradation of the solid hardness,delayed deformations can be observed even when the stress state is kept constant(Oldecop and Alonso,2007).In rockfill dams,post-construction settlements have been recorded over decades(Sowers et al.,1965; Scherard and Cooke,1987;Brauns et al.,1980;Soriano and Sanchez,1999;Naylor et al.,1997;Wang,2000;Zhou et al., 2007,2011;Yin,2009).The process of degradation of the solid hardness is mainly inf l uenced by the history of mechanical,thermal,and chemical weathering,the mineralogical composition of the grains,the micro-crack distribution within the particles,the hydro-chemical reaction of the pore fluid at crack tips,and the local stress concentrations(e.g.,Brauns et al.,1980;Li,1988;Alonso and Oldecop,2000;Oldecop and Alonso,2001,2007;Fang,2005;Ovalle et al.,2013, 2015).Various constitutive models for simulating the mechanical behavior of rockfill materials have been developed based on the framework of continuum theories such as nonlinear elasticity,elastoplasticity,generalized plasticity,and hypoplasticity(e.g.,Duncan and Chang,1970;Justo and Durand,2000;Oldecop and Alonso,2001,2007;Xiao et al., 2011;Zhang et al.,2007;Bauer,2009;Sun and Huang, 2009;Bauer et al.,2012;Wang et al.,2014;Fu et al.,2014).

The aim of the present paper is to compare the performance oftheextendedgeneralizedplasticity(EGP)modelproposedby Wang et al.(2014)with a simplified hypoplastic model for rockfill materials,which is based on the original model by Bauer(2009).Bothmodels canref l ect the inf l uence ofthe mean stress on the incremental stiffness,the peak friction angle,and the dilatancy angle.Furthermore,in both models,the so-called solid hardness is considered as a key parameter for describing the state of weathering and the time-dependent degradation of therockfillmaterial.Incontrasttothehardnessofasinglegrain, the solid hardness introduced in the constitutive models is def i ned for an assembly of rockfill particles under isotropic compression.The solid hardness was originally introduced by Bauer(1996)as a material constant for unweathered granular materials and then extended by Bauer in 2009 to a moregeneral concept for modeling creep and stress relaxation of coarsegrained,weathered,and moisture-sensitive rockfill materials. The suitability of the solid hardness as a key parameter for ref l ecting the compression behavior for a wide range of pressures was also verified by discrete element simulations,e.g.,for unbreakable granular materials(Oquendo et al.,2009),for an assembly of two-dimensional(2-D)breakable discs(Fu et al., 2012),and for arbitrarily shaped three-dimensional(3-D)particles(Laufer,2015).While in the original generalized plasticity model the isotropic compression curve in the semilogarithmic representation is described by a constant inclination,the more consistent compression law described by Bauer (1996)was adopted into the concept of generalized plasticity for modeling rockfill materials by Chen et al.(2011).Although the solid hardness is a key parameter in both models,the functions proposed for modeling the degradation of the solid hardness are different.

The paper is organized as follows:In section 2,the EGP model proposed by Wang et al.(2014)is outlined for the case of monotonic loading under axisymmetric stress conditions. The model is calibrated based on the experimental results from Fu and Ling(2009)with coarse-grained broken sandstone, which was also used in the Cihaxia concrete face rockfill dam. The results obtained from numerical simulations of triaxial compression tests under different lateral stress states and creep tests under different deviatoric stress states are compared by means of experiments.In section 3,the hypoplastic constitutive equations relevant to axisymmetric stress paths are presented.Calibration and numerical simulations are outlined for the same material and stress paths as those carried out for the generalized plasticity model.The performance of the two different models is compared and discussed in section 4. Finally,conclusions are given in section 5.

Throughout the paper,bold lowercase italic letters denote vectors,bold uppercase italic and Greek letters denote secondorder tensors,and bold uppercase italic letters with～above the letters denote fourth-order tensors.Indices on vector and tensor components refer to an orthonormal Cartesian basis ei(i=1,2,3).Operations and symbols are def i ned as follows: A?B=AijBklei?ej?ek?el, AB=AikBkjei?ej, ~A∶B= AijklBklei?ej,A∶B=AijBij,and trA=Aii.Here,the summation convention over repeated indices is employed.A superposed circle denotes an objective time derivative,e.g.,?A,and a superposed dot denotes the material time derivative,e.g., ˙A=dA/dt.For the EGP model in section 2,the sign convention in soil mechanics is adopted,i.e.,compressive stress and strain are positive.On the other hand,for the hypoplastic model in section 3 compressive stresses and strains and their rates are taken as negative as in the sign convention of rational continuum mechanics.Moreover,in hypoplasticity, logarithmic strains are used,but in all f i gures the numerical results are presented in engineering strains.

2.Material modeling using extended generalized plasticity(EGP)

The theory of generalized plasticity was first introduced by Zienkiewicz and Mroz(1984),and later extended by Pastor et al.(1990)for simulating the strain-stress response of granular soils.An essential feature of the concept of generalized plasticity is that neither yield nor plastic potential surfaces are explicitly def i ned.The gradients of these surfaces are used instead of the functions themselves.With generalized plasticity models,irreversible deformations can be described in any stress state and for both loading and unloading.

Based on the framework of generalized plasticity,various extensions of the model by Pastor et al.(1990)have been proposed for ref i ned simulation of mechanical properties of granular soils,including anisotropy,unsaturated conditions, degradation phenomena,and pressure-level dependency(e.g., Pastor,1991;Ling and Liu,2003;Fernandez Merodo et al., 2004;Ling and Yang,2006;Manzanal et al.,2011;Weng, 2014).For analyses of the instantaneous deformation of rockfill materials,generalized plasticity models have been developed(e.g.,Xu et al.,2012;Dong et al.,2013;Fu et al., 2014).In most of these models a Cam-Clay type dilatancy equation is adopted for simulating the dilatancy behavior. Chen et al.(2010),however,found that particle breakage during shearing plays an important role in the shear-induced compaction of rockfills under higher pressure,and it may be underestimated by such stress-dilatancy theories.With consideration of the above,an improved stress-dilatancy equation for rockfill materials was recently proposed by Wang et al.(2014).Concerning the simulation of creep deformation of rockfill materials,little experience has been gained to date in applying the generalized plasticity model.For modeling creep,an EGP model was proposed by Wang et al.(2014, 2015).It is brief l y outlined below.

2.1.Constitutive model

The elastoplastic material behavior is described in the EGP model by an incremental relationship between the effective stress increment dσ and the total strain increment dε,which can be represented as follows(e.g.,Pastor et al.,1990; Zienkiewicz et al.,1999;Mira et al.,2009):

The inverse form reads as follows:

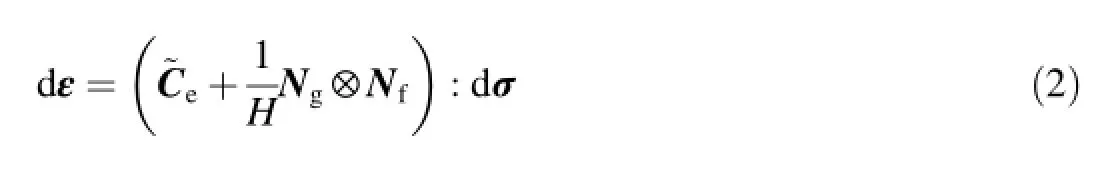
where~Depis the elastoplastic stiffness tensor,~Deis the elastic stiffness tensor,~Ceis the inverse of~De,Ngis the normalized plastic flow direction tensor,Nfis the normalized loading direction tensor,and H is the plastic modulus.For axisymmetric, deviatoric loading conditions,the relationships between the volumetric strain increment dεv,the deviatoric strain increment dεs,the mean stress increment dp,and the deviatoric stress increment dq can be represented in a matrix form as follows:

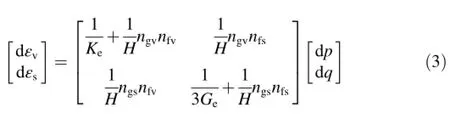
where the elastic parameters Keand Geare the tangential bulk module and the shear module,respectively,ngsand ngvare the components of vector ng,and nfsand nfvare the components of vector nf.In particular,Kecan be expressed as Ke=2Ge(1+ν)/ (3-6ν)and Geis assumed to be Ge=G0pa(p/pa)m,where p is the mean stress,pais the atmospheric pressure,and ν,G0,and m are constitutive constants(e.g.,Mase and Mase,1999;Liu et al., 2005).

The plastic flow direction vector ngand loading direction vector nfare expressed as follows:

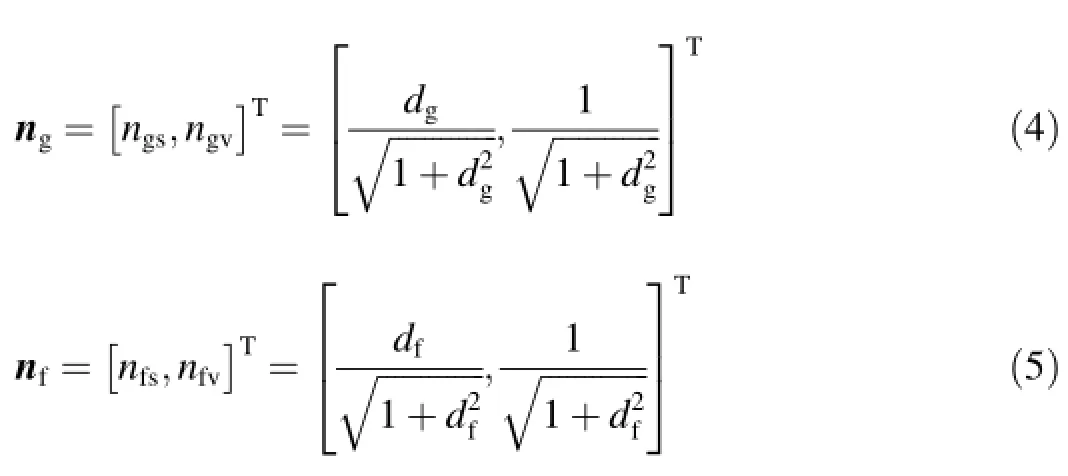
where the dilatancy ratio dgis the ratio of the plastic volumetric strain increment dεpvto the plastic deviatoric strain increment dεps,i.e.,dg=dεpv/dεps.In the EGP model proposed by Wang et al.(2014),the dilatancy ratio dgand the scalar function dfare expressed as follows:

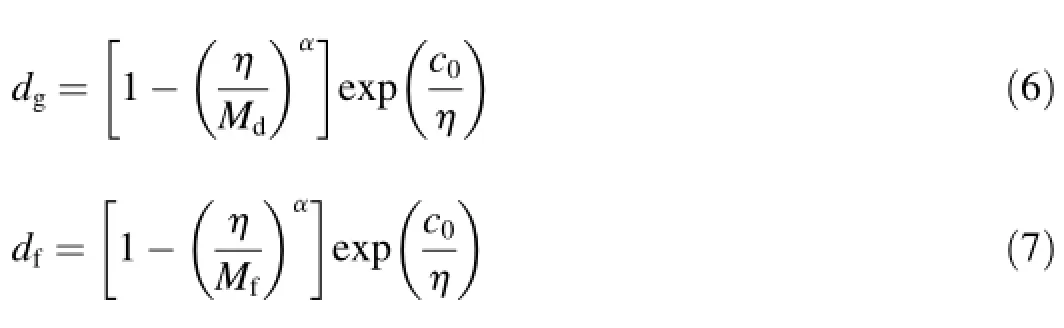
where η is the stress ratio,i.e.,η=q/p,with q=σ11-σ33and the mean stress p=(σ11+σ22+σ33)/3;α and c0are constants;and Mdisthedilatancy stressratio,i.e., Md=6sinψ/(3-sinψ),with ψ being the mobilized friction angle for the state of maximum εv.The inf l uence of pressure on ψ is described by the following approximation function:

where ψ0is the initial value of ψ when p=pa,and Δψ is a constitutive constant.The peak stress ratio Mfis def i ned as Mf=6sinφf/(3-sinφf),where φfis the pressure-dependent peak friction angle and described by the approximation function as follows:

where φf0is the value of φfwhen p=pa,and Δφfis a constitutive constant.

Based on investigation of experimental data of creepsensitive rockfill materials,the following representation for the plastic modulus H was proposed by Wang et al.(2014):

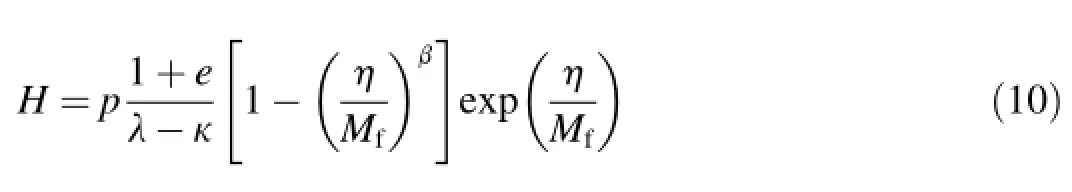
where β is the parameter of the plastic modulus,e is the current void ratio,and k and λ are constitutive parameters related to isotropic compression under loading and unloading, respectively.The state variable k can be expressed as follows (Wang et al.,2014):

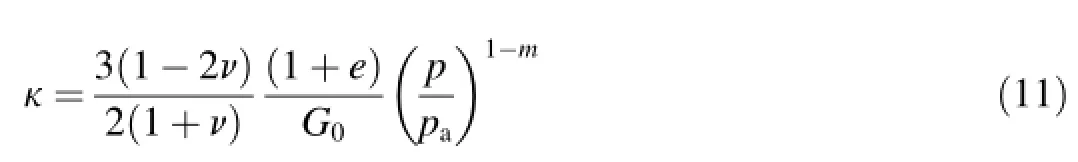
In many constitutive models(e.g.,Oldecop and Alonso, 2001;Salim and Indraratna,2004;Yao et al.,2004;Alonso and Cardoso,2010),the parameter λ describes the inclination of the compression curve in the e-lnp representation as illustrated in Fig.1(a).

Chen et al.(2011)suggested that parameter λ should be a pressure-dependent parameter according to the compression law proposed by Bauer(1996),which reads for monotonic isotropic compression as follows:

where hs0and n are parameters related to the solid hardness of a grain skeleton,the quantity p=(σ11+2σ22)/3 denotes the mean pressure for axisymmetric stress states,and e0is the void ratio for p≈0.It should be noted that in Chen et al.(2011) hs0in Eq.(12)is replaced by the initial solid hardness hs0,i.e., hs0=hs0/3,so that in the present model by Wang et al.(2014) the compression law can be expressed as follows:

Then the pressure-dependent parameter λ*can be expressed as follows(Fig.1(b)):

According to Chen et al.(2011),the current value of the void ratio e in Eq.(10),Eq.(11),and Eq.(14)is calculated using the relation e=e0-(1+e0)εv.

In order to model creep deformation of water-sensitive rockfill materials,a time-dependent degradation of the solid hardness is considered,i.e.,in Eq.(13)is replaced by a time-dependent state variableas fi rst proposed by Bauer (2009):

With respect to the time-dependent quantityone obtains the following equation from Eq.(12):

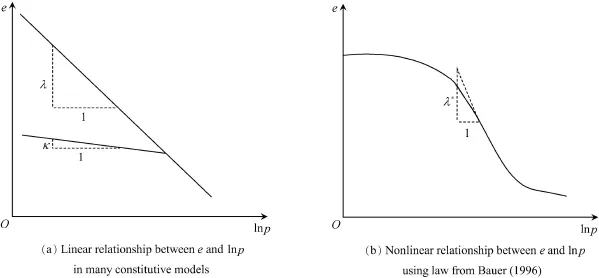
Fig.1.Various ways of modeling isotropic compression.

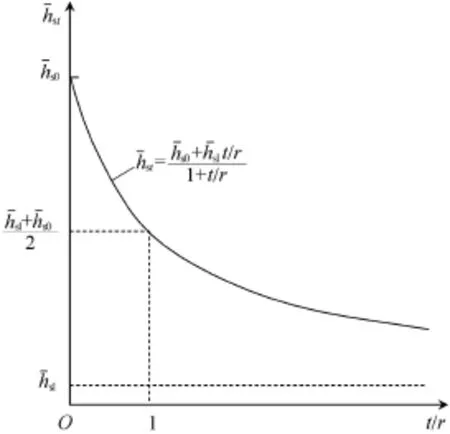
Fig.2.Sketch of time-dependent degradation of solid hardness in EGP model by Wang et al.(2014).

where λtis the time-and pressure-dependent compression parameter of the extended model by Wang et al.(2015).In this section(·)tdenotes a time-dependent quantity.Then for creep states the strain increment of creep deformation can be expressed as follows:

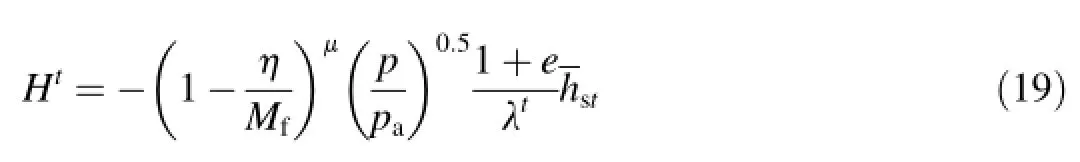
where μ is a dimensionless parameter.

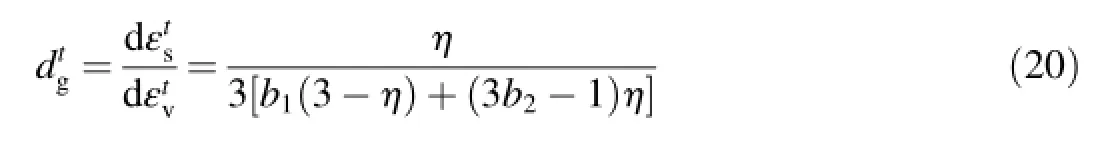
where b1and b2are constitutive constants.

2.2.Model calibration

The EGP model includes a total of 17 constitutive constants:e0,,n,G0,m,ν,φf0,Δφf,ψ0,Δψ,α,β,,r,b1,b2, and μ.The calibration procedure is based on the experimental data obtained by Fu and Ling(2009)with coarse-grained broken sandstone.Triaxial tests with cylindrical specimens with a diameter of 30 cm and a height of 70 cm were carried out under water-saturated and drained conditions.The particle size ranged between 0.1 mm and 60 mm and the mean grain diameter d50was 20 mm.

The parameters e0,,and n can be calibrated using Eq.(13) to f i t the e-lnp curve of isotropic compression test result.More details of the calibration procedure ofand n can be found in Bauer(1996).The elastic constants G0and m can be determined by f i tting the initial inclination of the stress-strain curve obtained during shearing.The Poisson's ratio ν of the rockfill material was assumed to be a constant in this study,i.e.,ν=0.3. The parameters,which relate to the mobilized friction angle, i.e.,φf0,Δφf,ψ0,and Δψ,can be calibrated from the approximation functions of φfand ψ.In particular,ψ can be determined according to the characteristic point related to the maximum volumetric strain,and φfcan be determined according to the peak of the curve of the mobilized friction angle φm(Fig.3(a)). With respect to the approximation functions of ψ and φfused, the results of curve f i tting are shown in Fig.3(b).With an increase of the lateral pressure of the specimens,the difference between ψ and φfdecreases,which means that the dilatancy behavior during shearing is in a certain way suppressed.This can be explained by particle breakage under higher pressures.

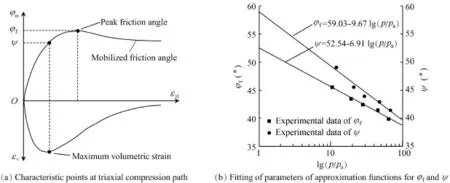
Fig.3.Calibration of parameters φf0,Δφf,ψ0,and Δψ of approximation functions of φfand ψ.

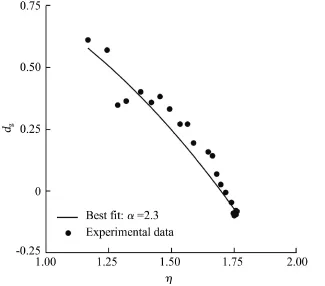
Fig.4.Fitting of parameter of approximation function of dg.

The dilatancy parameter α can be determined by f i tting the experimental data with the function for the dilatancy ratio in Eqs.(6)and(7)as shown in Fig.4.The plastic modulus parameter,β,can be calibrated by back analysis of shear test results.The parameters of solid hardness degradation,and r,can be determined by f i tting the data of creep deformation under isotropic stress states according to Eq.(14).The two parameters related to the flow rule of creep deformation,b1and b2,can be obtained by fi tting thecurve in the creep deformation stage.The parameter μ of creep deformation can also be calibrated from the creep test under isotropic compression,i.e.,from thecurve.

The calibrated values of the constitutive parameters are summarized in Table 1.

2.3.Numerical results

For numerical simulations,the EGP model proposed by Wang et al.(2014)was implemented in the finite element code Abaqus.Element tests were performed for monotonic isotopic compression,triaxial compression,and creep states under different deviatoric stress levels.All the numerical simulations were carried out with the same set of constitutive parameters shown in Table 1.In Figs.5—7 the numerical results and experimental data from Fu and Ling(2009)are represented by solid curves and dots,respectively.In particular,Fig.5(a) shows the mobilized friction angle against the axial strain for different lateral stresses.The corresponding volume strain curves are shown in Fig.5(b).Creep deformation at different axial stresses under the lateral stress values of σ22=1200 kPa and σ22=2000 kPa are shown in Figs.6 and 7,respectively.A detailed interpretation of the performance of the model is given in section 4.

3.Material modeling using hypoplasticity(HYP)

In contrast to the concept of elastoplasticity,the concept of hypoplasticity(HYP)does not require introduction of a switch function to distinguish between loading and unloading (Kolymbas,1991).In particular,in the framework of HYP, pressure-and density-dependent incremental stiffness,strain softening,and critical states as well as inelastic material properties can be described using a single incrementally nonlinear tensor-valued function of the rate type(Wu et al.,1996; Gudehus,1996;Bauer,1996).For ref i ned modeling of complex cyclic loading paths,a so-called intergranular strain was introduced as an additional state variable into HYP by Niemunis and Herle(1997).Microstructure effects like grain rotation and coupled stresses are modeled with an extended micro-polar HYP description(e.g.,Tejchman and Bauer,1996; Huang and Bauer,2003;Ebrahimian and Bauer,2012).Aspects of thermodynamic principles in HYP are discussed for example by Svendsen et al.(1999)and Gudehus et al.(2011). Formodeling mechanicalpropertiesofweathered and moisture-sensitive coarse-grained rockfills,a time-dependent, irreversible degradation of the solid hardness was introduced into the concept of HYP by Bauer(2009).In this model creep and stress relaxation are described in a consistent manner.

3.1.Constitutive model

In classical,nonpolar HYP the objective stress rateis described by an isotropic tensor-valued function,F,which depends on the current Cauchy stress tensor,σ,the strain rate tensor,˙ε,and for a ref i ned description of properties of the microstructure it can also depend on additional state variables, si,and their rates,Variables(i=1,2,…,n)are of importance for materials with time-dependent properties such as creep and stress relaxation.Thus,the general form of the evolution equation can be represented as follows:

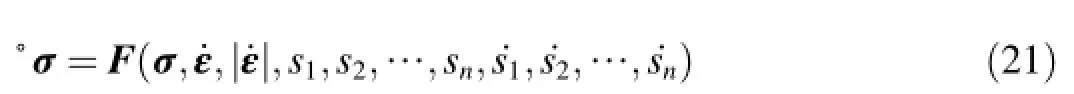
With respect to the norm of the strain rate,the constitutive equation(Eq.(21))is incrementally nonlinear and describes a dissipative material behavior.Depending on the material properties to be described,different specif i cations of function F can be found in the literature about hypoplasticity.For weathered and moisture-sensitive rockfill materials an appropriate hypoplastic model was first proposed by Bauer(2009).In this model,the key parameter used to describe the current state of weathering is the solid hardness, hst.The degradation of hstwith time is given by the following evolution equation:

where hstdenotes the current value of the solid hardness,is the rate of solid hardness,hswrepresents the f i nal value of the solid hardness after degradation,and the parameter c controls the velocity of degradation.Experiments indicate that thedelayed deformation of stressed rockfills,i.e.,the progressive particle breakage and contact plastif i cation,is mainly inf l uenced in a rather complex manner by interactions between the state of weathering,the humidity,the local stress state,and the pre-compaction of the material(e.g.,Brauns et al.,1980;Li, 1988;Alonso and Oldecop,2000;Fang,2005;Oldecop and Alonso,2007;Ovalle et al.,2013,2015).For the sake of simplicity,c is assumed to be a constant in this paper.With respect to the initial state,i.e.,at t=0 and hst(t)=hs0,the integration of Eq.(22)yields the following equation:

Table 1Constitutive parameters for EGP model.

Fig.5.Results of triaxial compression tests for different values of lateral stress σ22using EGP.

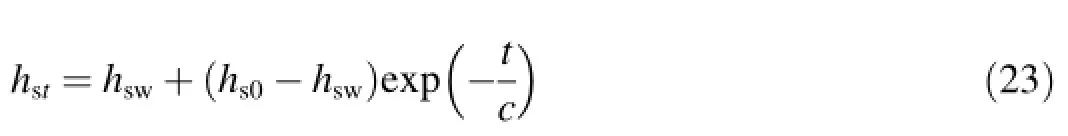
Although the compression law in Eq.(15)has the same structure in the EGP model and the HYP model,the approximation of the contained time-dependent solid hardness,hst,is different for both models as also illustrated in Figs.2 and 8.

As the available experimental data from Fu and Ling (2009)are not suff i cient for the calibration of the model by Bauer(2009),a simplified version of the model was used in this study.In particular,for the function F in Eq.(21)the following state quantities are considered:

where e is updated according to the evolution equation.For axisymmetric loading,e.g.,for isotropic loading and triaxial loading paths,which were considered in this study,the objective stress rate is equal to the material time derivative of the Cauchy stress tensor,i.e.,.The particular representations of the components of Eq.(24)relatedto monotonic and axisymmetric loading processes are as follows:

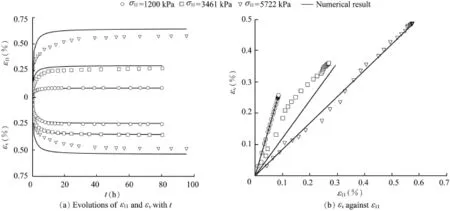
Fig.6.Creep deformation under a constant lateral stress of σ22=1200 kPa and for three different values of axial stress σ11using EGP.

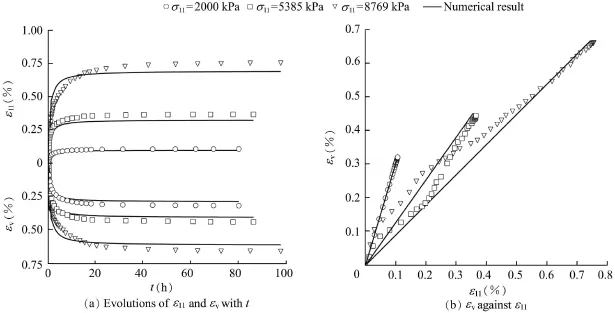
Fig.7.Creep deformation under a constant lateral stress of σ22=2000 kPa and for three different values of axial stress σ11using EGP.

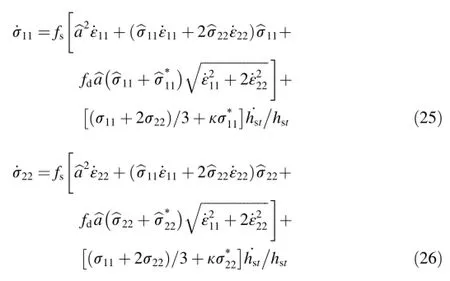
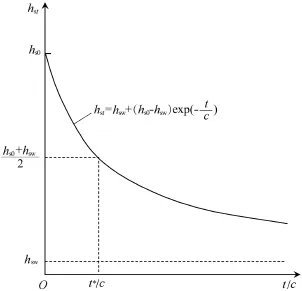
Fig.8.Sketch of time-dependent degradation of solid hardness in model by Bauer(2009).

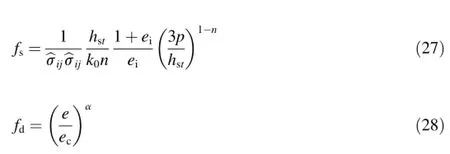
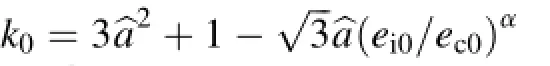
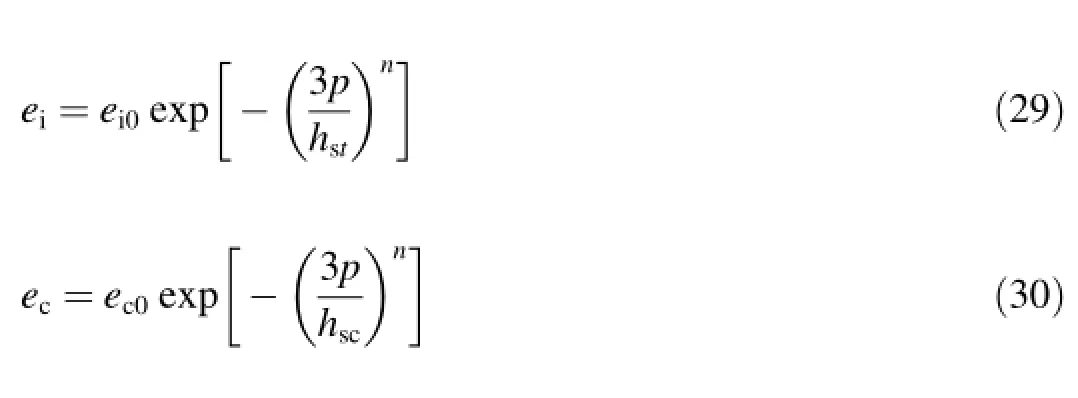
where ei0and ec0are the corresponding values for the nearly stress-free state.In contrast to previous versions,the solid hardness hstfor isotropic compression is different from hscfor the critical void ratio curve as outlined in section 3.2.

3.2.Model calibration

The proposed hypoplastic constitutive model includes ten constants:hs0,n,hsw,c,k,φc,ei0,ec0,hsc,and α.In particular, the initial solid hardness hs0and the parameter n can be calibrated based on the experimental data obtained from a virgin isotropic compression test as already mentioned in section 2.2.With respect to the value ofin Table 1 and the different scaling ofandone obtains=3×40=120 MPa.Depending on the available experimental data,the f i nal value of the solid hardness,hsw, can be calibrated in different ways.One opportunity is to consider the reduction of the void ratio during creep under isotropic stress conditions and to calculate hswfrom the analytical solution(Bauer,2009):

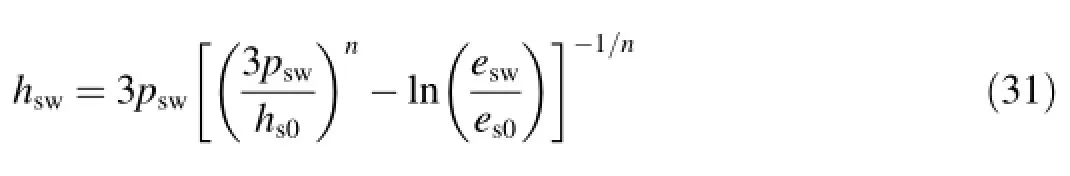
wherepswistheconstantisotropicstressundercreep,andes0and eswdenote the void ratios at the beginning and the end of the creep experiment,respectively.The velocity of degradation of thesolidhardnessiscontrolledbytheparameterc,whichcanbe calibrated from the degradation curve in Fig.8.In particular, from Eq.(23)and for the state where half of the amount of degradation of the solid hardness appears,the corresponding timet*canbederived,i.e.,t*=-c ln（1/2).Thus,thevalueofc can be calculated by the following equation:

From Eqs.(25)and(26)it can be seen that k scales the amount of the deviatoric stress of the creep term of the constitutive equations.Thus,k has a signif i cant inf l uence on the creep deformation and can be adapted to the inclination of the εv-ε11curve,as shown in Figs.12 and 13.The critical friction angle φcis def i ned for the triaxial compression test in the residual state.Although a critical state was not reached in the experiments by Fu and Ling(2009),the investigations by Xiao et al.(2014)indicate that the critical friction angle is independent of the pressure level.With respect to the fact that with an increase of the conf i ning stress σ22the difference between the peak friction angle and the critical friction angle diminishes, a value of φc=40?can be estimated from Fig.9(a).The values for the maximum void ratio ei0,the critical void ratio ec0,and the parameter hscwere also estimated by back analysis.In particular,for different lateral stresses the predicted critical void ratio was f i tted with the approximation function in Eqs.(29)and (30)as shown in Fig.10(a).It should be mentioned that the best fi tting of the predicted critical void ratios yields a value forthat is different from the solid hardness obtained from an isotropic compression test.In contrast to the assumption made in previous hypoplastic models,the value of hscis therefore different from the value of the solid hardness hs0in the present study.This can be explained by a more pronounced grain crushing under deviatoric loading than under isotropic loading. The corresponding curves for the pressure-dependent maximum void ratio eiand the critical void ratio ecare shown in Fig.10(b).The parameter α of the density function fdin Eq.(28)has a signif i cant inf l uence on the magnitude of the peak friction angle and the dilatancy behavior.Meanwhile,the peak friction angle and dilatancy angle are predef i ned by an approximation function in the EGP model;these quantities come out as a prediction of the HYP model.In particular,the density function fdtriggers the dependency of the peak friction angle and dilatancy angle on the current void ratio and pressure level as outlined in more details by Bauer(1996).Thus,the parameter α can be calibrated for instance from the peak friction angles obtained from triaxial compression tests under different lateral stresses as shown in Fig.9.

For the numerical simulations discussed in the next section, the constitutive parameters for the proposed hypoplastic model are summarized in Table 2.

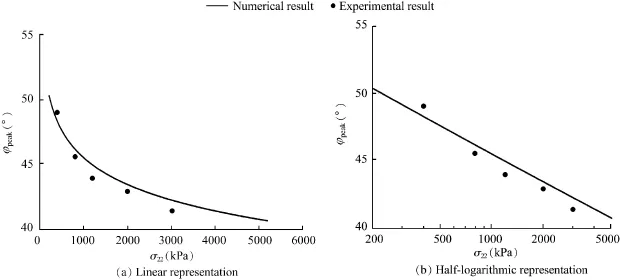
Fig.9.Calibration of peak friction angle φpeakdepending on conf i ning stress σ22.

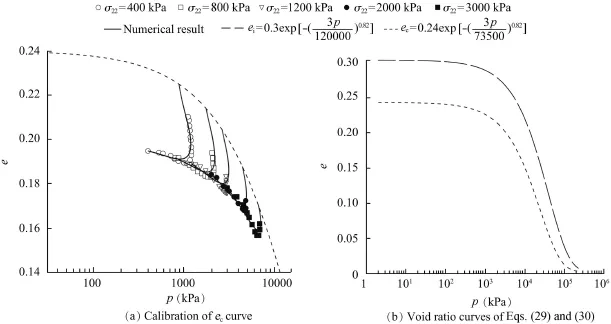
Fig.10.Pressure-dependent maximum void ratio eiand critical void ratio ec.

3.3.Numerical results

The same numerical simulations for the EGP model shown in section 2.3 were also carried out for the HYP model outlined in section 3.1.All the numerical results shown in Figs.11—13 are compared with the experimental results from Fu and Ling(2009).In particular,the solid curves and the markers represent the numerical results and experimental data,respectively.The performances of the HYP model and the EGP model are discussed in the following section.

4.Comparison of EGP model with HYP model

In the previous sections,two different constitutive models, the EGP model by Wang et al.(2014)and a simplified hypoplastic model(HYP)by Bauer(2009),were calibrated for creep-sensitive rockfill materials,and numerical simulations of triaxial tests and creep tests have been compared with experiments.

Based on the experimental data available for the present investigations,some model parameters could only be estimated using optimization procedures and back analysis.It is well known that calibration is an inverse problem and for highly nonlinear material models the results obtained from back analysis are not unequivocal.In this context,a high separability of the constitutive parameters by individual calibration equations is desirable,which is also convenient for a better interpretation of the physical meaning of the individual parameters asdiscussedforinstancefortheHYPmodelbyBauer(1996).In the EGP model,however,some material parameters are included in the calibration equations in a complex manner, which makes the calibration more complicated.

Table 2Constitutive parameters for simplified hypoplastic model.

The numerical results obtained for monotonic triaxial compression illustrated in Figs.5 and 11 show that both models can ref l ect the inf l uences of the mean stress on the incremental stiffness,the peak friction angle,and the dilatancy angle.In particular,the results predicted with the EGP model are in rather strong agreement with experiments for triaxial compressions up to the peak state.This agreement is supported by the approximation functions used in EGP for the dilatancy-dependent Eq.(8),and for the peak friction angle, i.e.,Eq.(9).For larger vertical compression,the experimental results indicate strain softening for lower values of lateral stress,which cannot be predicted with the EGP model. Furthermore,dilatancy is unlimited for monotonic compression,and for higher pressure levels the incremental stiffness at the beginning of deviatoric loading is lower than the experimental one.In contrast,the HYP model also predicts strain softening after the stress peak as the proposed constitutive model is based on critical-state soil mechanics(e.g.,Gudehus, 1996;Bauer,2000).Fig.11(a)shows that strain softening is more pronounced for a lower pressure level,indicating that numerical results of the model are in agreement with the experimental data.On the other hand,the volumetric strain behavior at the beginning of triaxial compression is less predictable with the HYP model than with the EGP model.

The simulation of creep tests was carried out for two different values of lateral stress σ22and for three different values of axial stress,as shown in Figs.6 and 12 for σ22=1200 kPa and in Figs.7 and 13 for σ22=2000 kPa.The rate of the axial creep strain and the rate of the volumetric strain diminish with an increase of time,which is predicted by both the EGP model(Figs.6(a)and 7(a))and the HYP model (Figs.12(a)and 13(a)).The experimental results show that, depending on the amount of the deviatoric stress,the creep deformation will become almost stable within one or two days. Long-term field observations,however,indicate that creep deformations of rockfill dams can last several decades (Oldecop and Alonso,2007).Oneexplanation ofthisphenomenon is that repeated rainwater inf i ltration into the dam body can initiate the continuation and acceleration of the propagation of micro-cracks in weathered rockfill particles, which leads to additional grain breakage and,as a consequence,to additional settlements of the rockfill material.In this case,the value of hswis no longer a material constant and for modeling of such a behavior a continuation of the degradation of hswcan be considered.

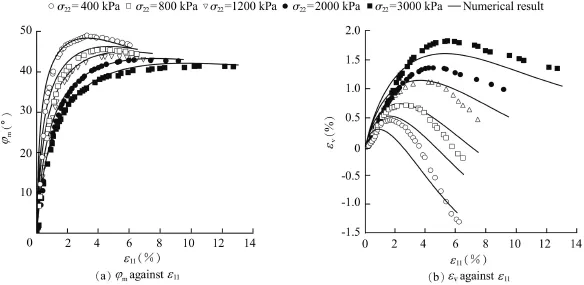
Fig.11.Results of triaxial compression tests for different values of lateral stress σ22using HYP.

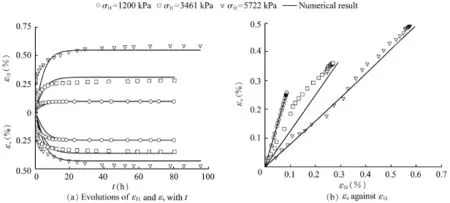
Fig.12.Creep deformation under a constant lateral stress of σ22=1200 kPa and for three different values of axial stress σ11using HYP.

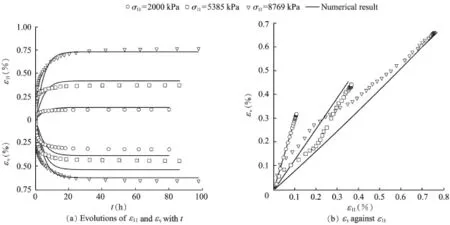
Fig.13.Creep deformation under a constant lateral stress of σ22=2000 kPa and for three different values of axial stress σ11using HYP.

The predicted εv-ε11relationships exhibit straight lines in both models(Figs.6(b),7(b),12(b),and 13(b)).It can be noted that for the creep test under isotropic stress states the model prediction agrees with the experimental data.However, under deviatoric stress states the experimental data from Fu and Ling(2009)show a nonlinear evolution.In contrast,the creep experiments carried out by Li(1988)and Fang(2005) under different deviatoric stress states show an almost linear relationship between εvand ε11,which was also well predicted with the hypoplastic model for weathered rockfill materials by Bauer et al.(2010,2012).Few experimental data are available in the literature and it is well known that the inaccuracy of experimental results might be caused by inhomogeneous specimen deformations.Thus,furtherexperimentalinvestigations are necessary to clarify the question of linearity.

5.Conclusions

In this paper the modeling of the mechanical behavior of creep-sensitive rockfill materials is described and compared for two different constitutive models.In particular,the extended generalizedplasticity(EGP)modelandasimplifiedhypoplastic (HYP)model are considered.The constitutive equations are represented for modeling monotonic and axisymmetric triaxial compression and creep under deviatoric stress states.For the EGP model,appropriate constitutive relationships are considered for the elastic stiffness tensor,the plastic flow direction tensor,theloadingdirectiontensor,andtheplasticmodulus.For modeling creep states,a modified creep modulus proposed by Wang et al.(2014)was used.With respect to the experimental data available for calibration,a simplified HYP version of the model originally proposed by Bauer was considered in this study.The proposed EGP model includes 17 constitutive constants and the HYP model includes 10 constants.The role of the constitutive constants and their dependence on various factors were analyzed.The constants were calibrated based on experimental data of coarse-grained broken sandstone.The solid hardness was considered in both models as a key parameter for describing the state of weathering of the rockfill material and it is def i ned in the sense of a continuum description.Creep deformations were described as a result of the time-dependent process of degradation of the solid hardness.The results of this study demonstrate that the concept of the solid hardness originally proposed in hypoplasticity can also be adapted to other classes of constitutive models.The numerical results obtained for simulation of triaxial compression tests under different lateral stresses and creep tests under different stress levels are in strong agreement with the experimental data.Both models are able to ref l ect the inf l uence of the mean stress on the incremental stiffness,the peak friction angle,and the dilatancy angle.For practical application,a simplified version with a reduced number of material parameters would be desirable,in particular for the EGP model.

Acknowledgements

The authors wish to thank the Nanjing Hydraulic Research Institute for providing experimental data,and Dr.Zhong-zhi Fu from the Nanjing Hydraulic Research Institute for helpful remarks.

Alonso,E.E.,Oldecop,L.A.,2000.Fundamentals of rockfill collapse.In: Rahardjo,H.,Toll,D.G.,Leong,E.C.,eds.,Proceedings of the 1st Asian Conference on Unsaturated Soils.Balkema Press,Rotterdam,pp.3—13.

Alonso,E.E.,Cardoso,R.,2010.Behavior of materials for earth and rockfill dams:Perspective from unsaturated soil mechanics.Front.Archit.Civ. Eng.China 4(1),1—39.http://dx.doi.org/10.1007/s11709-010-0013-6.

Bauer,E.,1996.Calibration of a comprehensive hypoplastic model for granular materials.Soils Found.36(1),13—26.

Bauer,E.,2000.Conditions for embedding Casagrande's critical states into hypoplasticity.Mech.Cohesive-Frictional Mater.5(2),125—148.http://dx.doi.org/ 10.1002/(SICI)1099-1484(200002)5:2＜125::AID-CFM85＞3.0.CO;2—0.

Bauer,E.,2009.Hypoplastic modeling of moisture-sensitive weathered rockfill materials.Acta Geotech.4,261—272.http://dx.doi.org/10.1007/ s11440-009-0099-y.

Bauer,E.,Fu,Z.Z.,Liu,S.H.,2010.Hypoplastic constitutive modeling of wetting deformation of weathered rockfill materials.Front.Archit.Civ. Eng.China 4(1),78—91.http://dx.doi.org/10.1007/s11709-010-0011-8.

Bauer,E.,Fu,Z.Z.,Liu,S.H.,2012.Inf l uence of pressure and density on the rheological properties of rockfills.Front.Struct.Civ.Eng.6(1),25—34. http://dx.doi.org/10.1007/s11709-012-0143-0.

Brauns,J.,Kast,K.,Blinde,A.,1980.Compaction effects on the mechanical and saturation behaviour of disintegrated rockfill.In:Proceedings of International Conference on Compaction.Laboratoire Central des Ponts et Chausees,Paris,pp.107—112.

Chen,S.S.,Han,H.Q.,Fu,H.,2010.Stressanddeformationbehavioursofrockfill under cyclic loading.Chin.J.Geotech.Eng.32(8),1151—1157(inChinese).

Chen,S.S.,Fu,Z.Z.,Han,H.Q.,Peng,C.,2011.An elastoplastic model for rockfill materials considering particle breakage.Chin.J.Geotech.Eng. 33(10),1489—1496(in Chinese).

Dong,W.X.,Hu,L.M.,Yu,Z.Y.,Lu¨,H.,2013.Comparison between Duncan and Chang's EB Model and the generalized plasticity model in the analysis of a high earth-rockfill dam.J.Appl.Math.1—12.http://dx.doi.org/ 10.1155/2013/709430.

Duncan,J.M.,Chang,C.Y.,1970.Nonlinear analysis of stress and strain in soils.J.Soil Mech.Found.Div.96(5),1629—1653.

Ebrahimian,B.,Bauer,E.,2012.Numerical simulation of the effect of interface friction of a bounding structure on shear deformation in a granular soil.Int.J.Numer.Anal.Methods Geomech.36(12),1486—1506.http:// dx.doi.org/10.1002/nag.1059.

Fang,X.S.,2005.TestStudyandNumericalSimulationonWettingDeformation of Gravel Sand.M.E.Dissertation.Hohai University,Nanjing(in Chinese).

Fernandez Merodo,J.A.,Pastor,M.,Mira,P.,Tonni,L.,Herreros,M.I., Gonzalez,E.,Tamagnini,R.,2004.Modelling of diffuse failure mechanisms of catastrophic landslides.Comput.Methods Appl.Mech.Eng. 193(27-29),2911—2939.http://dx.doi.org/10.1016/j.cma.2003.09.016.

Fu,H.,Ling,H.,2009.Experimental Research on the Engineering Properties of the Fill Materials Used in the Cihaxia Concrete Faced Rockfill Dam. Nanjing Hydraulic Research Institute,Nanjing(in Chinese).

Fu,Z.Z.,Chen,S.S.,Liu,S.H.,2012.Hypoplastic constitutive modeling of the wetting induced creep of rockfill materials.Sci.China Technol.Sci.55(7), 2066—2082.http://dx.doi.org/10.1007/s11431-012-4835-4.

Fu,Z.Z.,Chen,S.S.,Peng,C.,2014.Modeling cyclic behavior of rockfill materials in a framework of generalized plasticity.Int.J.Geomech.14(2), 191—204.http://dx.doi.org/10.1061/(ASCE)GM.1943-5622.0000302.

Gudehus,G.,1996.A comprehensive constitutive equation for granular materials.Soils Found.36(1),1—12.

Gudehus,G.,Jiang,Y.M.,Liu,M.,2011.Seismo-and thermodynamics of granular solids.Granul.Matter 13(4),319—340.http://dx.doi.org/10.1007/ s10035-010-0229-0.

Huang,W.,Bauer,E.,2003.Numerical investigation of shear localization in a micro-polar hypoplastic material.Int.J.Numer.Anal.Methods Geomech. 27(4),325—352.http://dx.doi.org/10.1002/nag.275.

Justo,J.L.,Durand,P.,2000.Settlement-timebehaviourofgranularembankments. Int.J.Numer.Anal.Methods Geomech.24(3),281—303.http://dx.doi.org/ 10.1002/(SICI)1096-9853(200003)24:3＜281::AID-NAG66＞3.0.CO;2-S.

Kolymbas,D.,1991.An outline of hypoplasticity.Archive Appl.Mech.61(3), 143—151.http://dx.doi.org/10.1007/BF00788048.

Laufer,I.,2015.Grain crushing and high-pressure oedometer tests simulated with the discrete element method.Granul.Matter 17(3),389—412.http:// dx.doi.org/10.1007/s10035-015-0559-z.

Li,G.X.,1988.Triaxial Wetting Experiments on Rockfill Materials Used in Xiaolangdi Earth Dam.Tsinghua University,Beijing.

Ling,H.I.,Liu,H.B.,2003.Pressure-level dependency and densif i cation behavior of sand through a generalized plasticity model.J.Eng.Mech. 129(8), 851—860. http://dx.doi.org/10.1061/(ASCE)0733-9399(2003) 129:8(851).

Ling,H.I.,Yang,S.T.,2006.Unified sand model based on the critical state and generalized plasticity.J.Eng.Mech.132(12),1380—1391.http:// dx.doi.org/10.1061/(ASCE)0733-9399(2006)132:12(1380).

Liu,M.C.,Gao,Y.F.,Huang,X.M.,2005.Study on elasto-plastic constitutive model of rockfills with nonlinear strength characteristics.Chin.J.Geotech. Eng.27(3),294—298(in Chinese).

Manzanal,D.,Pastor,M.,Fernandez Merodo,J.A.,2011.Generalized plasticity state parameter-based model for saturated and unsaturated soils.Part II:Unsaturated soil modeling.Int.J.Numer.Anal.Methods Geomech. 35(18),1899—1917.http://dx.doi.org/10.1002/nag.983.

Mase,G.T.,Mase,G.E.,1999.Continuum Mechanics for Engineers,second ed.CRC Press,London.

Mira,P.,Tonni,L.,Pastor,M.,Fernandez Merodo,J.A.,2009.A generalized midpoint algorithm for the integration of a generalized plasticity model for sands.Int.J.Numer.Methods Eng.77(9),1201—1223.http://dx.doi.org/ 10.1002/nme.2445.

Naylor,D.J.,Maranha,J.R.,Maranha das Neves,E.,Veiga Pinto,A.A.,1997. A back-analysis of Beliche Dam.Geotechnique 47(2),221—233.http:// dx.doi.org/10.1680/geot.1997.47.2.221.

Niemunis,A.,Herle,I.,1997.Hypoplasticmodelforcohesionlesssoilswithelastic strainrange.Mech.Cohesive-frictionalMater.2(4),279—299.http://dx.doi.org/ 10.1002/(SICI)1099-1484(199710)2:4＜279::AID-CFM29＞3.0.CO;2—8.

Oldecop,L.A.,Alonso,E.E.,2001.A model for rockfill compressibility. Geotechnique 51(2),127—139.

Oldecop,L.A.,Alonso,E.E.,2007.Theoretical investigation of the timedependent behaviour of rockfill.Geotechnique 57(3),289—301.http:// dx.doi.org/10.1680/geot.2007.57.3.289.

Oquendo,W.F.,Mu~noz,J.D.,Lizcano,A.,2009.Oedometric test,Bauer's law and the micro-macro connection for a dry sand.Comput.Phys.Commun. 180(4),616—620.http://dx.doi.org/10.1016/j.cpc.2009.01.002.

Ovalle,C.,Dano,C.,Hicher,P.Y.,2013.Experimental data highlighting the role of surface fracture energy in quasi-static conf i ned comminution. Int.J.Fract.182(1),123—130.http://dx.doi.org/10.1007/s10704-013-9833-4.

Ovalle,C.,Dano,C.,Hicher,P.Y.,Cisternas,M.,2015.An experimental framework for evaluating the mechanical behavior of dry and wet crushable granular materials based on the particle breakage ratio.Can.Geotech. J.52(5),587—598.http://dx.doi.org/10.1139/cgj-2014-0079.

Pastor,M.,Zienkiewicz,O.C.,Chan,A.H.C.,1990.Generalized plasticity and the modelling of soil behaviour.Int.J.Numer.Anal.Methods Geomech. 14(3),151—190.http://dx.doi.org/10.1002/nag.1610140302.

Pastor,M.,1991.Modelling of anisotropic sand behaviour.Comput.Geotech. 11(3),173—208.http://dx.doi.org/10.1016/0266-352X(91)90019-C.

Salim,W.,Indraratna,B.,2004.A new elastoplastic constitutive model for coarse granular aggregates incorporating particle breakage.Can.Geotech. J.41(4),657—671.http://dx.doi.org/10.1139/t04-025#.VqI6k_krK70.

Scherard,J.L.,Cooke,J.B.,1987.Concrete-face rockfill dam:I.Assessment.J. Geotech.Geoenviron.Eng.113(10),1096—1112.http://dx.doi.org/ 10.1061/(ASCE)0733-9410(1987)113:10(1096).

Soriano,A.,Sanchez,F.J.,1999.Settlements of railroad high embankments. In:Proceedings of 12th European Conference on Soil Mechanics and Geotechnical Engineering. AA Balkema Publishers,Amsterdam, pp.1885—1890.

Sowers,G.F.,Williams,R.C.,Wallace,T.S.,1965.Compressibility of broken rock and settlement of rockills.In:Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering.University of Toronto Press,Montreal,pp.561—565.

Sun,H.Z.,Huang,M.S.,2009.A constitutive model for coarse granular material incorporating both strain work-softening and dilatancy.J.Tongji Univ.(Nat.Sci.)37(6),727—733(in Chinese).

Svendsen,B.,Hutter,K.,Laloui,L.,1999.Constitutive models for granular materials including quasi-static frictional behaviour:Toward a thermodynamic theory of plasticity.Continuum Mech.Thermodyn.11(4),263—275. http://dx.doi.org/10.1007/s001610050115.

Tejchman,J.,Bauer,E.,1996.Numerical simulation of shear band formation with a polar hypoplastic constitutive model.Comput.Geotech.19(3), 221—244.http://dx.doi.org/10.1016/0266-352X(96)00004-3.

Wang,Y.,2000.Analysis on rheology mechanism and study method of rockfill.Chin.J.Rock Mech.Eng.19(4),526—530(in Chinese).

Wang,Z.J.,Chen,S.S.,Fu,Z.Z.,2014.Viscoelastic-plastic constitutive model of creep deformation for rockfill materials.Chin.J.Geotech.Eng.36(12), 2188—2194.http://dx.doi.org/10.11779/CJGE201412005(in Chinese).

Wang,Z.J.,Chen,S.S.,Fu,Z.Z.,2015.Dilatancy behaviors and a generalized plasticity model of rockfill materials.Rock Soil Mech.36(7),1931—1938. http://dx.doi.org/10.16285/j.rsm.2015.07.013(in Chinese).

Weng,M.C.,2014.A generalized plasticity-based model for sandstone considering time-dependent behavior and wetting deterioration.Rock Mech.Rock Eng.47(4),1197—1209.http://dx.doi.org/10.1007/s00603-013-0466-8.

Wu,W.,Bauer,E.,Kolymbas,D.,1996.Hypoplastic constitutive model with critical state for granular materials.Mech.Mater.23(1),45—69.http:// dx.doi.org/10.1016/0167-6636(96)00006-3.

Xiao,Y.,Liu,H.L.,Zhu,J.G.,2011.A 3D bounding surface model for rockfill materials.Sci.China Technol.Sci.54(11),2904—2915.http://dx.doi.org/ 10.1007/s11431-011-4554-2.

Xiao,Y.,Liu,H.L.,Chen,Y.M.,Jiang,J.S.,Zhang,W.G.,2014.Testing and modeling of the state-dependent behaviors of rockfill material.Comput. Geotech.61,153—165.http://dx.doi.org/10.1016/j.compgeo.2014.05.009.

Xu,B.,Zou,D.G.,Liu,H.B.,2012.Three-dimensional simulation of the construction process of the Zipingpu concrete face rockfill dam based on a generalized plasticity model.Comput.Geotech.43,143—154.http:// dx.doi.org/10.1016/j.compgeo.2012.03.002.

Yao,Y.P.,Sun,D.A.,Luo,T.A.,2004.A critical state model for sands dependent on stress and density.Int.J.Numer.Anal.Methods Geomech. 28(4),323—337.http://dx.doi.org/10.1002/nag.340.

Yin,Z.Z.,2009.Stress and deformation of high earth and rock-fill dams.Chin. J.Geotech.Eng.31(1),1—14(in Chinese).

Zhang,B.Y.,Jia,Y.A.,Zhang,Z.L.,2007.Modified Rowe's dilatancy law of rockfill and Shen Zhujiang's double yield surfaces elastoplastic model. Chin.J.Geotech.Eng.29(10),1443—1448(in Chinese).

Zhou,W.,Hu,Y.,Yang,S.C.,2007.Fabric theory on creep deformation mechanism for high rockfill dams.Chin.J.Geotech.Eng.29(8), 1274—1278(in Chinese).

Zhou,W.,Hua,J.J.,Chang,X.L.,2011.Settlement analysis of the Shuibuya concrete-face rockfill dam.Comput.Geotech.38(2),269—280.http:// dx.doi.org/10.1016/j.compgeo.2010.10.004.

Zienkiewicz,O.C.,Mroz,Z.,1984.Generalized plasticity formulation and applications to geomechanics.In:Mechanics of Engineering Materials. John Wiley&Sons,New York,pp.655—679.

Zienkiewicz,O.C.,Chan,A.H.C.,Pastor,M.,Schref l er,B.A.,Shiomi,T., 1999.Computational Geomechanics with Special Reference to Earthquake Engineering.John Wiley&Sons,New York.

Received 2 September 2015;accepted 15 March 2016

This work was supported by the CRSRI Open Research Program(Grant No.CKWV2016375/KY),the National Natural Science Foundation of China (Grants No.51609182,51379130,and 51209141),and the Chinese Scholarship Council.

*Corresponding author.

E-mail address:erich.bauer@tugraz.at(Erich Bauer).

Peer review under responsibility of Hohai University.

http://dx.doi.org/10.1016/j.wse.2016.11.005

1674-2370/?2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

?2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).