Likely Limit Sets of a Class of p-order Feigenbaum’s Maps?
WANG WEIAND LIAO LI
(1.Institute of Mathematics,Jilin University,Changchun,130012)
(2.Institute of Applied Physics and Computational Mathematics,Beijing,100094)
Likely Limit Sets of a Class of p-order Feigenbaum’s Maps?
WANG WEI1AND LIAO LI2
(1.Institute of Mathematics,Jilin University,Changchun,130012)
(2.Institute of Applied Physics and Computational Mathematics,Beijing,100094)
A continuous map from a closed interval into itself is called ap-order Feigenbaum’s map if it is a solution of the Feigenbaum’s equation fp(λx)=λf(x). In this paper,we estimate Hausdor ffdimensions of likely limit sets of somep-order Feigenbaum’s maps.As an application,it is proved that for any 0<t<1,there always exists ap-order Feigenbaum’s map which has a likely limit set with Hausdor ff dimension t.This generalizes some known results in the special case of p=2.
Feigenbaum’s equation,Feigenbaum’s map,likely limit set,Hausdor ff dimension
1 Introduction
This paper is concerned with the generalized Feigenbaum’s equation

where f is a continuous map of the closed interval[0,1]into itself,and fpis the p-fold iteration of f.This equation was first studied in[1],and its original form is

which was posed by Feigenbaum[2?3]for explaining a universal phenomenon occurring in an interval mapping family with one parameter.
A continuous map f on the closed interval[a,b]is said to be univallecular,if there exists α∈(a,b)such that f is strictly decreasing on[a,α]and strictly increasing on[α,b].
In the sequel,we use I to denote the interval[0,1].
De fi nition 1.1Letfbe a continuous map ofIinto itself.We callfap-order Feigenbaum’s map,if it is a solution of(1.1),such thatf(0)=1andf|[λ,1]is univallecular.We call Feigenbaum’s mapfnon-univallecular,iffitself is not univallecular.
In the past more than thirty years,the researches on Feigenbaum’s maps have aroused one’s grave concern(see[1–10]).More authors studied the existence of Feigenbaum’s maps, and only a few of them were concerned with likely limit sets of Feigenbaum’s maps.In[9], the Hausdor ffdimension of a likely limit set of an even analytic function which is similar to Feigenbaum’s map was estimated.It was pointed out in[10]that for any t∈(0,1),there is always a 2-order Feigenbaum’s map which has a likely limit set with Hausdor ffdimension t.As an extension of the results in[10],we study the likely limit sets of a class of p-order Feigenbaum’s maps.The main results are given in Theorems 3.1 and 3.2.
2 Preliminaries
Milnor[11]introduced the concept of a likely limit set for a continuous map of a compact manifold as follows.
Let M be a compact manifold(possibly with boundary),and f be a continuous map from M into itself.
De fi nition 2.1The likely limit set off,denoted by Λ(f),or simply Λ,is the smallest closed invariant subset ofMwith the propertyω(x,f)?Λ for each pointx∈Moutside of a set of Lebesgue’s measure zero,whereω(x,f)denotes theω-limit set of the pointxunderf(see[12]for the de fi nition).
As indicated in[11],the likely limit set always exists and it is the unique maximal attractor(in the sense of Milnor).Because such an attractor accumulates the asymptotic behaviors of almost all points,it is very necessary to study this type of subsets.
Recall that a subset E of M is said to be minimal for f,if
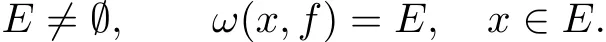
As is well known,the minimal set is closed,non-void and invariant,and no proper subset has these three properties(see[12]).Therefore,if E is a minimal set with ω(x,f)?E for almost all x∈M,then
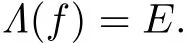
Let(X,d)be a compact metric space.Denote by|E|the diameter of a subset E of X, i.e.,

where the in fi mum is taken over all(countable)δ-cover{Ui}of E.
The Hausdor ffs-dimensional out measure of E is de fi ned by

Such an r is uniquely determined,called the Hausdor ffdimension of E and denoted by dimE (see[9]).
A mapping φ:Rn→Rnis called a contraction,whereRnis the n-dimensional Euclidean space,if there exists a c<1 such that
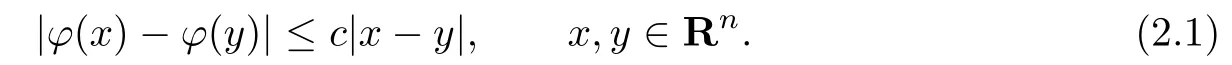
We call the in fi mum value of c satisfying(2.1)the ratio of the contraction.
The following two lemmas are useful.
Lemma 2.1([9],Theorem 8.3)Letφ1,φ2,···,φmbe contractions onRn.Then there exists a unique non-empty compact setEsuch that

is a transformation of subsets ofRn.Furthermore,for any non-empty compact subsetFofRn,the iteratesφk(F)converge toEin Hausdor ffmetric ask→∞.
Lemma 2.2([9],Theorem 8.8)Letφ1,···,φmbe contractions onRfor which the open set condition holds,i.e.,there is a bounded open intervalUsuch that

3 The Main Results and Their Proofs
The following lemma comes from Theorem 3.1 in[8],which gives the characteristics of non-univallecular Feigenbaum’s maps.
Lemma 3.1Letf0be a continuous map on[λ,1]with0<λ<1,andp≥2be an integer.If
(i)there exists anα∈(λ,1)such thatf0(α)=0andf0is strictly decreasing on[λ,α]and strictly increasing on[α,1];
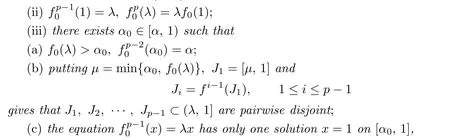
then there is a uniquep-order non-univallecular Feigenbaum’s mapfwithf|[λ,1]=f0.
Conversely,iff0is the restriction on[λ,1]of ap-order non-univallecular Feigenbaum’s map,then(i)–(iii)hold.
Theorem 3.1Letfbe ap-order non-univallecular Feigenbaum’s map such thatf(α)=0for someα∈(λ,1),andg=f|[α,1].IffisC1on[λ,α]and[α,1],and such that
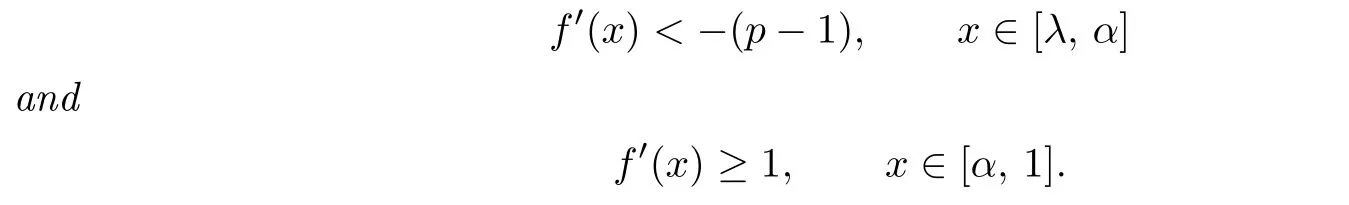
wheref′(x)denotes the derivative ifxis in the interior of an interval,and left derivative or right derivative ifxis an endpoint of a closed interval,then Λ(f)is a minimal set offsuch thats≤dimΛ(f)≤t,where
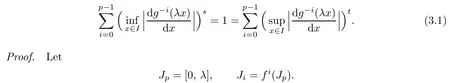
Since f is a p-order non-univallecular Feigenbaum’s map,it follows from Lemma 3.1 that Ji?[α,1]for 1≤i≤p?1.De fi ne φi:I→I by

Then φiis a contraction for each i.Set
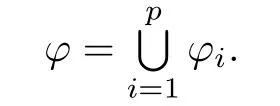
We know from Lemma 3.1 that for each i,φi(I)=Jiand J1,J2,···,Jpare pairwise disjoint.Thus φ satis fies the open condition.By Lemmas 2.1 and 2.2,there exists a unique non-empty compact set E such that
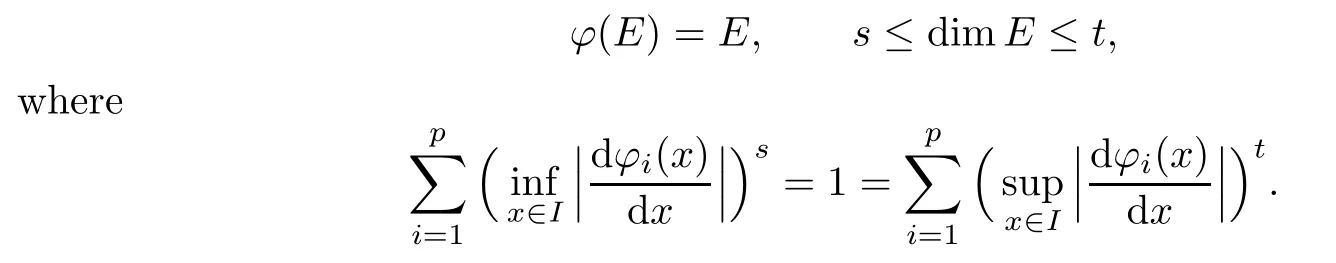
By the de fi nition of φi,we see that this is exactly(3.1).So in order to complete the proof of the theorem,it suffices to show that

Since φp(x)∈Jp,it follows that f?φp(x)∈[α,1].So,by the de fi nition of φ1,we have

This gives the first equality of the lemma.
For each i=1,···,p?1,setting f to act on both sides of the equality
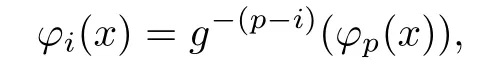
we immediately get the latter equalities.
Lemma 3.3For anyk>0,

is an invariant set off,i.e.,f(φk(I))?φk(I).

Proof.Let x∈I and 1≤i≤p.By Lemma 3.2,one has
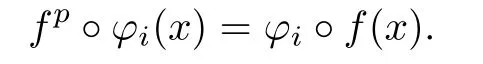
Using this equality repeatedly we know that
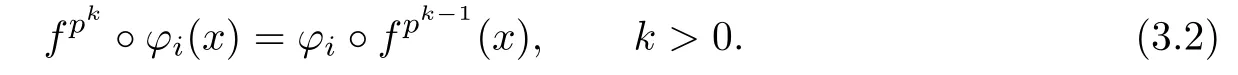
If for each r=1,2,···,k,we all have

then from(3.2),it follows that
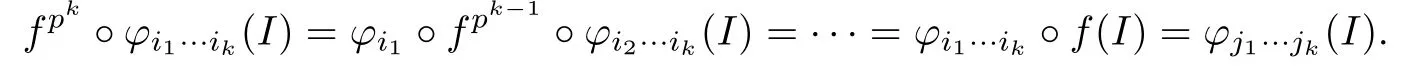
Note that f(I)=I.One can see that the lemma holds for this special case.Assume that there exists some r,1≤r≤k,such that iq=jqfor q<r,but irjr.Repeatedly applying (3.2)again,we know that ft·pr?1?φi1···ik(I),0<t<p?1 has the form φl(shuí)1···lrlr+1···lk(I), where lq=jq,1≤q≤r.Continuing this procedure,we must get some n,such that
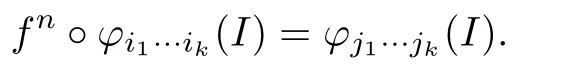
The proof of Lemma 3.4 is completed.
We now proceed to prove Theorem 3.1.In order to get the equality

we first prove
(1)For almost all x∈I,ω(x,f)?E.
To do this,it suffices to show that for almost all x∈I in the sense of Lebesgue the sequence{fm(x)}approaches to E for m→∞.
Denote

For each i=1,2,···,p?1,de fi ne ψi:J→J by
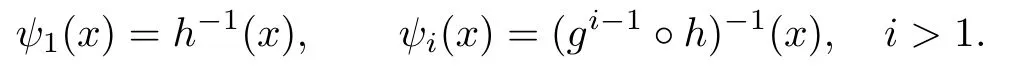
Since h(J)?J and by the hypotheses of the theorem,gi?1?h(J)?J for 1<i≤p?1,it follows that for each i,ψiis well de fi ned.By a simple calculation,we see that ψi(x)<1 for i=1,2,···,p?1 and x∈J.So each ψiis contracted.Also,we easily see that
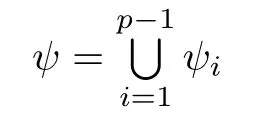
satis fies the open set condition.By Lemmas 2.1 and 2.2,there exists a unique non-empty compact set F0such that
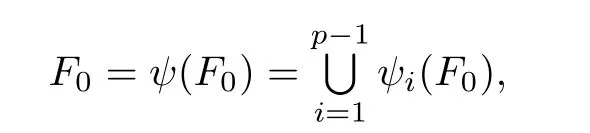
and dimF0≤r,where r is de fi ned by

By a calculation,we get
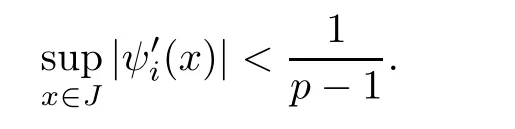
Applying this to(3.3)gives dimF0≤r<1.So L(F0)=0,where L(·)denotes the Lebesgue measure.Set
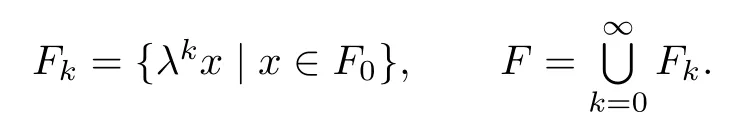
We also have
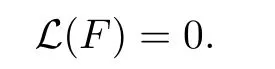
It is easy to check by induction that f restricted to any closed interval of the form [λn+1,λnα]or[λnα,λn]is monotone.If K is such an interval,then
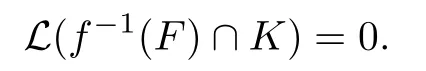
This is because we can find real numbers M>δ>0,such that δ<|f′(x)|<M for x∈K. Furthermore,since f has at most countable monotone intervals,it follows that
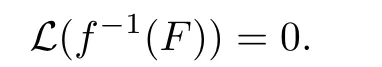
By induction,we know that
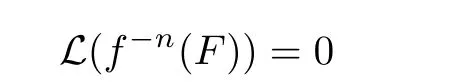
always holds true for any n>0.Set
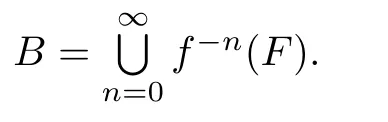
We see that
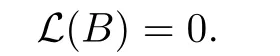
Therefore,I?B contains almost all the points in I.
ClaimFor any n≥1 and any x∈I?B,there exists an mn>0 such that fmn(x)∈φn(I).
We use the induction.Let x∈I?B and n=1.If x∈φ(I),then f(x)∈φ2(I)?φ(I), and we may take m1=1.If otherwise,then x∈[λ,1]?B?φ(I).Noting that
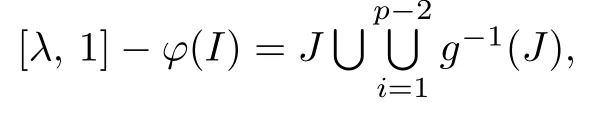
we have fk(x)∈J?F0for some k≥0.We may assume x∈J?F0.Since
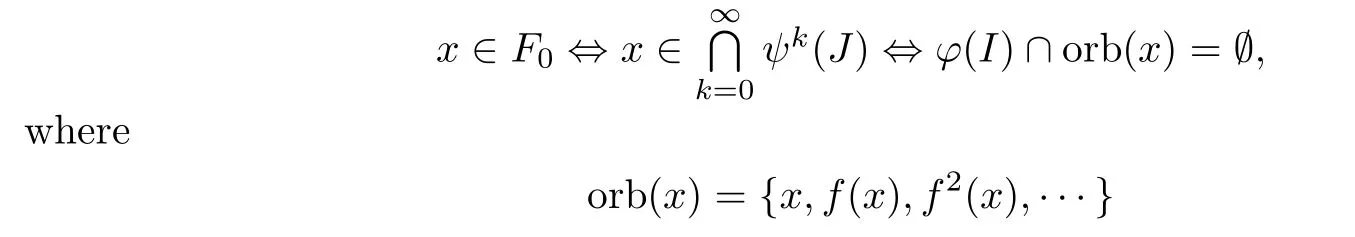
denotes the orbit of x,it follows that there exists an m1>0 such that fm1(x)∈φ(I).Then the Claim is true for n=1.
Assume that the Claim holds for n≥1.By Lemma 3.4,without loss of generality,we assume that fmn(x)∈[0,λn].Set
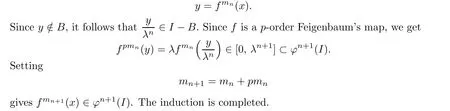
Combining the Claim with Lemma 3.3,we know that for any x∈I?B and n>0,there exists a k≥0 such that fm(x)∈φn(I)holds true for all m≥k.Thus from
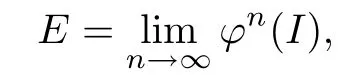
we see that for m→∞the sequence{fm(x)}approaches to E.
(2)E is a minimal set of f.
By the de fi nition we know that for each i the contraction ratio of φi≤λ,so the contraction ratio of φi1···ik≤λk.It follows that diamφi1···ik(“diam”denotes the diameter) converges to zero uniformly for ir∈{1,2,···,p},1≤r≤k as k→∞.Let x∈E.For any y∈E and any open set V containing y,since

there exist φi1···ik(I)and φj1···jk(I)such that x∈φi1···ik(I),y∈φj1···jk(I)?V.By Lemma 3.4,there exists an n>0 such that
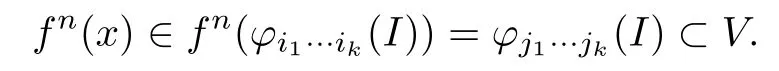
This shows y∈ω(x,f),and then E?ω(x,f).By(3.4)and Lemma 3.3,f(E)?E.Since E is closed,we also have ω(x,f)?E,and so
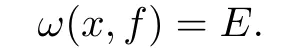
From the arbitrariness of x,we know that E is a minimal set of f.
Combining(1)with(2),by De fi nition 2.1,we know that
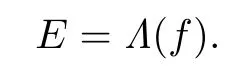
We complete the proof of Theorem 3.1.
Theorem 3.2For anyt∈(0,1),there exists ap-order non-univallecular Feigenbaum’s mapfsuch that
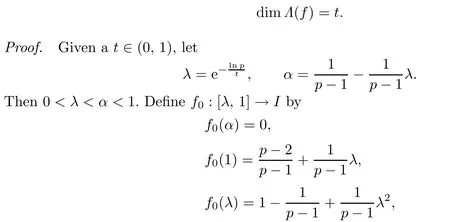
and f0is linear on[λ,α]and[α,1].It is easily to check that f0satis fies all the conditions of Lemma 3.1,and then there exists a unique p-order non-univallecular Feigenbaum’s map f such that
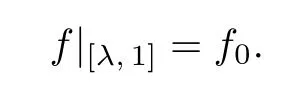
Also,by the de fi nition of f0,we see that

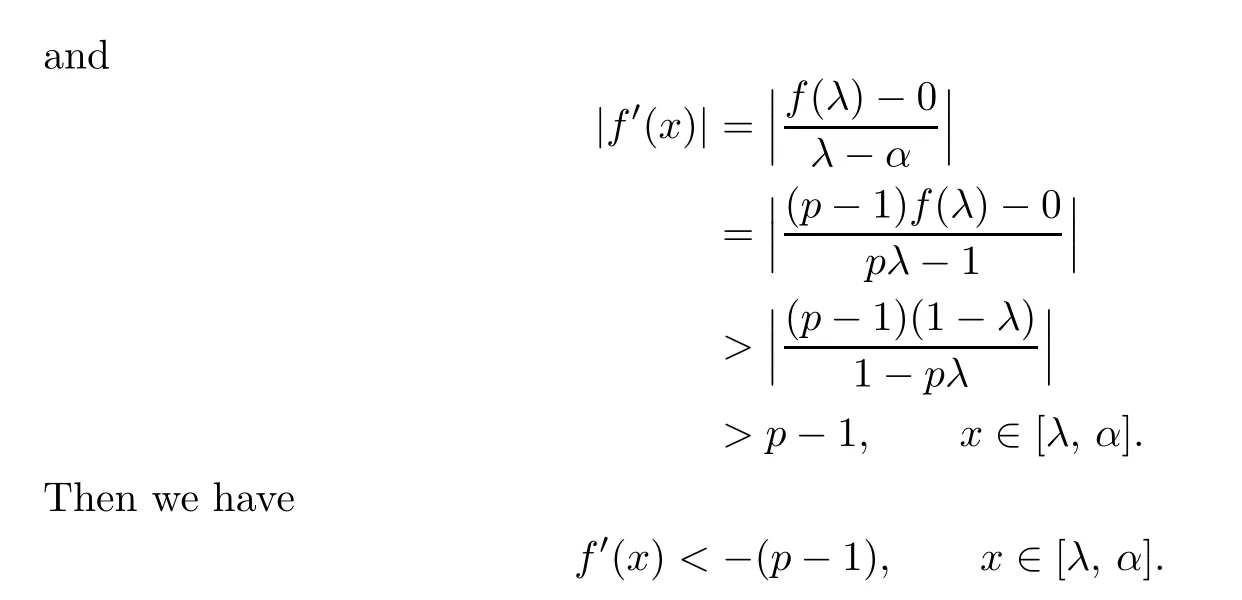
By Theorem 3.1 and a simple calculation,we get
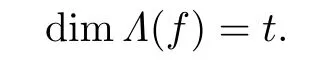
[1]Eckmann J P,Epstein H,Wittwer P.Fixed points of Feigenbaum’s type for the equation fp(λx)=λf(x).Comm.Math.Phys.,1984,93:496–516.
[2]Feigenbaum M.Qauntitative universality for a class of nonlinear transformations.J.Statist. Phys.,1978,19:25–52.
[3]Feigenbaum M.The universal metric properties of nonlinear transformations.J.Statist.Phys., 1979,21:669–706.
[4]Yang L,Zhang J Z.The second type of Feigenbaum’s functional equation.Sci.China,1986, A29:1252–1263.
[5]Campanino M,Epstein H.On the existence of Feigenbaum’s fixed point.Comm.Math.Phys., 1981,79:261–302.
[6]Epstein H.New proofs of the existence of the Feigenbaum’s functions.Comm.Math.Phys., 1986,106:395–426.
[7]Liao G F.Solutions on the second type of Feigenbaum’s functional equations.Chinese Ann. Math.,1988,A9:649–654.
[8]Liao G F,Wang L D,Zhang Y C.p-order Feigenbaum’s maps.Northeast.Math.J.,2004,20: 284–290.
[9]Falconer K J.The Geometry of Fractal Sets.Cambridge and New York:Cambridge Univ. Press,1985.
[10]Huang G F,Wang L D,Liao G F.A note on the unimodal Feigenbaum’s maps.Internat.J. Modern Phys.,2009,B23:3101–3111.
[11]Milnor J.On the concept of attrator.Comm.Math.Phys.,1985,99:177–195.
[12]Block L S,Coppel W A.Dynamics in One Dimension:Lecture Notes in Math.vol.1513. Berlin:Springer-Verlag,1992.
Communicated by Lei Feng-chun
39B52
A
1674-5647(2012)02-0137-09
date:Sept.6,2010.
The NSF(10771084)of China.
 Communications in Mathematical Research2012年2期
Communications in Mathematical Research2012年2期
- Communications in Mathematical Research的其它文章
- A Penalty Approach for Generalized Nash Equilibrium Problem?
- Computing Numerical Singular Points of Plane Algebraic Curves?
- Stability of Global Solution to Boltzmann-Enskog Equationwith External Force?
- Analysis of Bifurcation and Stability on Solutions of a Lotka-Volterra Ecological System with Cubic Functional Responses and Di ff usion?
- Stability of Fredholm Integral Equation of the First Kind in Reproducing Kernel Space?
- Trivariate Polynomial Natural Spline for 3D Scattered Data Hermit Interpolation?
