NUMERICAL MODELING PURIFICATION PERFORMANCE OF POT TEST*

DAI Yu

Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes of Ministry of Education, Hohai University, Nanjing 210098, China

College of Mechanics and Materials Science, Hohai University, Nanjing 210098, China, E-mail: daiyu@hhu.edu.cn

WANG De-guan, ZHANG Jin-feng

College of Environmental, Hohai University, Nanjing 210098, China

LUAN Qing-hua

College of Water Conservancy and Hydropower, Hebei University of Engineering, Handan 056021, China

NUMERICAL MODELING PURIFICATION PERFORMANCE OF POT TEST*

DAI Yu

Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes of Ministry of Education, Hohai University, Nanjing 210098, China

College of Mechanics and Materials Science, Hohai University, Nanjing 210098, China, E-mail: daiyu@hhu.edu.cn

WANG De-guan, ZHANG Jin-feng

College of Environmental, Hohai University, Nanjing 210098, China

LUAN Qing-hua

College of Water Conservancy and Hydropower, Hebei University of Engineering, Handan 056021, China

(Received March 8, 2010, Revised July 26, 2010)

A three-dimensional mathematical model was developed to simulate the pollutant removal efficiency of the soil and plants in the pot test. The advection, dispersion, diffusion, adsorption, biochemical reaction and plant uptake processes were taken into account in the model. The three-dimensional modified Richards equation was used in simulating flow field. The mass balance law was employed in deriving the equation for pollutant transport, where the diffusion and dispersion were described with the Fick-type law, the adsorption was macroscopically expressed as form isotherm, and the bio-chemical degradation process was assumed to follow the Monod kinetics. The mathematical model was descretized by the finite element numerical method. In the pot test, the hydraulic loading was assumed to have the intermittent pattern simulating the rainfall duration and the occurrence of frequency, and the concentrations of pollutants in the influent and effluent were measured. The computed overall removal rates for the CODCrand TN in four cases are in the range of 90.62% - 95.43% and 85.01% - 96.46%, respectively. The differences between the computed and tested overall removal rates for the CODCrand TN are smaller than 5%. The time-varying oscillation pattern of the concentrations of the CODCrand TN were rationally simulated, which showed that the model presented in this article could be used to assess the pollutant removal efficiency of the soil and plants in related cases.

pot test, numerical modelling, pollutant removal efficiency, experiments

1. Introduction

Pot test has been commonly used in the scientific research for various purposes, such as finding out the methods to enhance nutrient utilization or contaminant extraction by the plant and the role of the bacteria in the enhancement of the nutrient utilization or contaminant extraction[1-4], the effect of soil compaction, soil amended with other materials and soil moisture on the nutrient uptake capacity of the plants[5,6], the plant response to the soil properties and the fertilise conditions under different watering conditions[7], the effect of nitrogen supply on potato leaf size[8], testing the possibility of using the mixture of the by-products from the industry like the slate industry and electric power plant wet scrubbers in growing plants or wetlands treatment[9,10], the evaluation of the relationships of the productivity-diversity of the plant species[11], the degradation mechanism of the pollutants under various conditions like loading rate, concentration of the pollutant, the temperature, the hydraulic retention time etc.[12], the removal capacity of the sorghum plants to heavy metal (Cd and Zn) and the possibilityof bio-monitoring the efficiency of phyto-remediation using parameters related to the size, activity and functional diversity of the soil microbial community[13]. The authors also carried out the pot test for testing the combined removal efficiency of the soil and plants, the role of the plants in removal of the various pollutants, the influence of the relative depth of the saturation part of the soil, and the temperature effect.

The results from those tests provided broad database for developing mathematical model to simulate the phenomena tested. The results from pot tests performed above were also used in calibrating and validating the corresponding numerical model.

There have been several kinds of mathematical models established for investigating the fates of pollutants moving with the groundwater or in the wetlands. The wetland models were usually conceptual models[14-16]. The groundwater pollution model basically described all the transportation and transformation processes of the pollutants in the groundwater and predicted the spatial and temporal distribution of the pollutants in the soil. Those models considered the advection-dispersion-diffusion process, assumed the pollutant being equilibrium partitioning between water and solid phases, and biochemical reaction being the first-order kinetics or the first-order Monod or double Monod kinetics. In order to make the model more universal, several models have been proposed based on the concept of the terminal electron acceptor process, and the so-called one-step model, two-step model and partial equilibrium approach model have been developed for predicting the translation and biochemical degradation of the pollutants in the soil[17-21].

In this work, according to the general principles mentioned above, under various rational assumptions, a three-dimensional mathematical model is established to simulate the pollutant removal efficiency of the soil and plants in the pot test, in which the advection, dispersion, diffusion, adsorption, biochemical reaction and plant uptake processes are taken into account. The mathematical model is discretized by the finite element numerical method and applied to the pot test. The numerical results agreed well with the experimental results, which showed that the model presented in this article could be used to assess the pollutant removal efficiency of the soil and plants in related cases.

2. Mathematical model

2.1 Mathematical model for water movement

2.1.1 Governing equation

The flow in the pot test filled with sand is governed by the Darcy law. As the soil in the pot is divided into two zones, i.e., the unsaturated zone and saturated zone, the water content is then considered as a time-dependant variable. Under the assumption that interaction between air and water is negligible, the flow in the pot is governed by a three-dimensional modified Richard equation[22],

where Ks(x, y, z ) is the saturated hydraulic conductivity, and Kr( h, x, y, z ) is the relative unsaturated hydraulic conductivity, which is defined as the ratio of the unsaturated hydraulic conductivity and the saturated hydraulic conductivity. In order to take the evapotranspiration of the plants growing in the pot into account, a sink term Sris added, which represents the volume of water uptake by the plants per unit time from a unit volume of soil. The sink termSris defined as

where the water response function α(h) is assumed as a dimensionless function of the soil water pressure head, 0 ≤ α(h)≤ 1, Spis the potential water uptake rate,［T?1］, and α(h) is assumed to be zero when the soil is close to saturation (h = hs, hsis the water head corresponding to saturation state) or the moisturein the soil is at or below wilting point ( h≤hw, hwis the water head corresponding to wilting state). The optimal water uptake is bounded by hu( huis the limiting water head below which plant roots start to uptake water from the soil at maximum transpiration rate) and hd( hdis another limiting water head below which plant roots can not uptake water from the soil at maximum transpiration rate), in whichα(h) has the value of one, and Sr( h) is equal to Sp, α( h) linearly varies from 0.0 to 1.0 as the value of h varies from hwto hd, and from 1.0 to 0.0 as the value of h varies from hutohs. The potential water uptake rate can be expressed as

where Lxand Lyare the horizontal dimensions of the root volume,, Lzis the depth of the root volume,Sdis the soil surface area related to each plant root,and Tis the potential transpiration rate,

2.1.2 Hydraulic parameters in unsaturated zone

In order to make the Eq.(1) a closed form, a set of relations among the hydraulic parameters, i.e., the water content θ(h) and relative hydraulic conductivity Kr( h, x, y, z) for the unsaturated zone are given as[22],

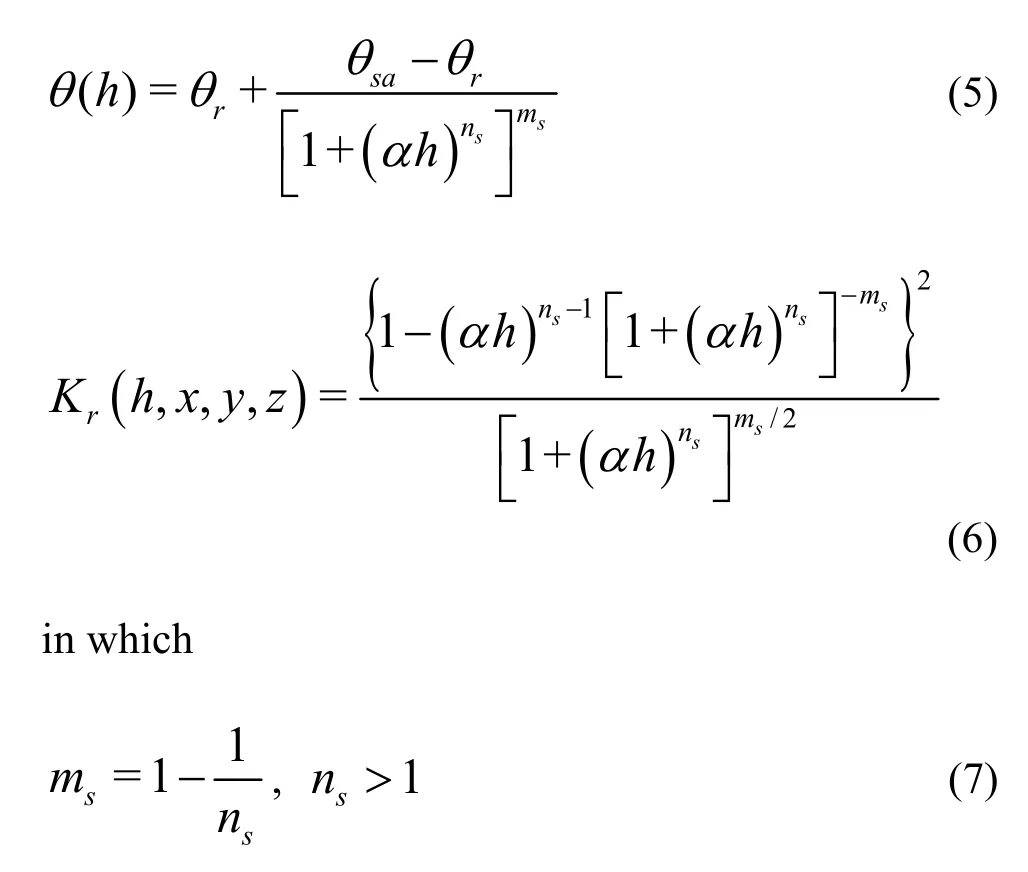
whererθ and θsadenote the residual and saturated water contents respectively, α, empirical coefficient, (1) The dispersive flux can be expressed by the Fick law.

(2) The biochemical degradation process follows the Monod kinetics.

(3) The transfer of pollutants between the solid and water by diffusion, adsorption, desorption, ion-exchange etc. is expressed macroscopically as the form of isotherm.

(4) The densities of the water and soil particles are constant.

(5) The rate of removal of pollutant by the plants is assumed to be expressed by the first-order reaction law.

Under those assumptions, the mathematical model may have the form

where ρwis the density of the water,, ρsthe density of the soil,, θwthe volumetric fraction of the water phase, θsthe volumetric fraction of the solid phase, C the concentration of the pollutants,, and F the pollutant concentration on the solid, and equals the mass of

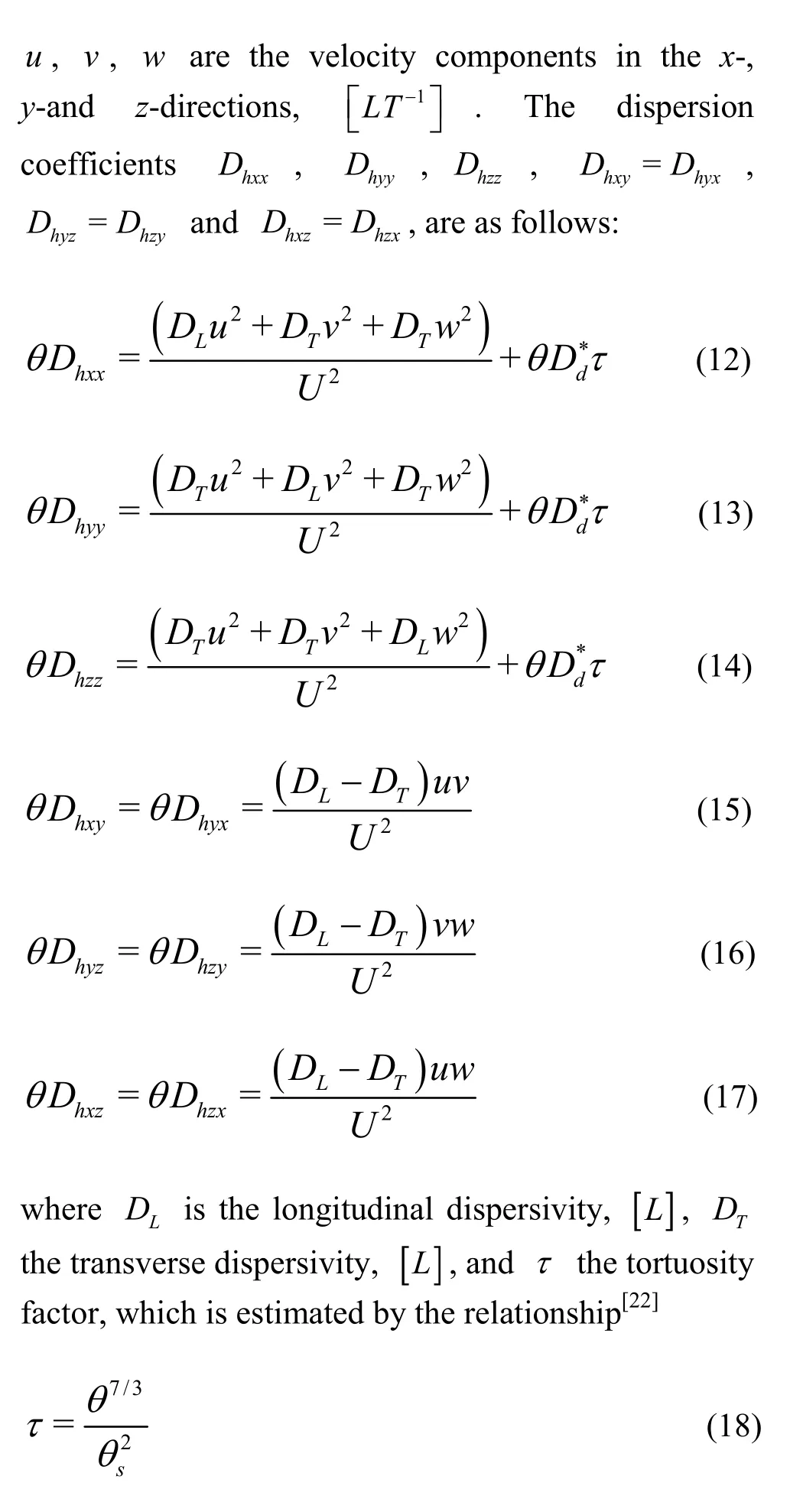
3. Finite element discretization

function, which satisfies the essential boundary conditions, hjthe nodal value of the h( x, y, z, t ) to be solved, and N the total number of nodes of the computational domain. On the basis of Eq.(19) and the principle of the Galerkin residual method, the Galerkin integral can be formulated as

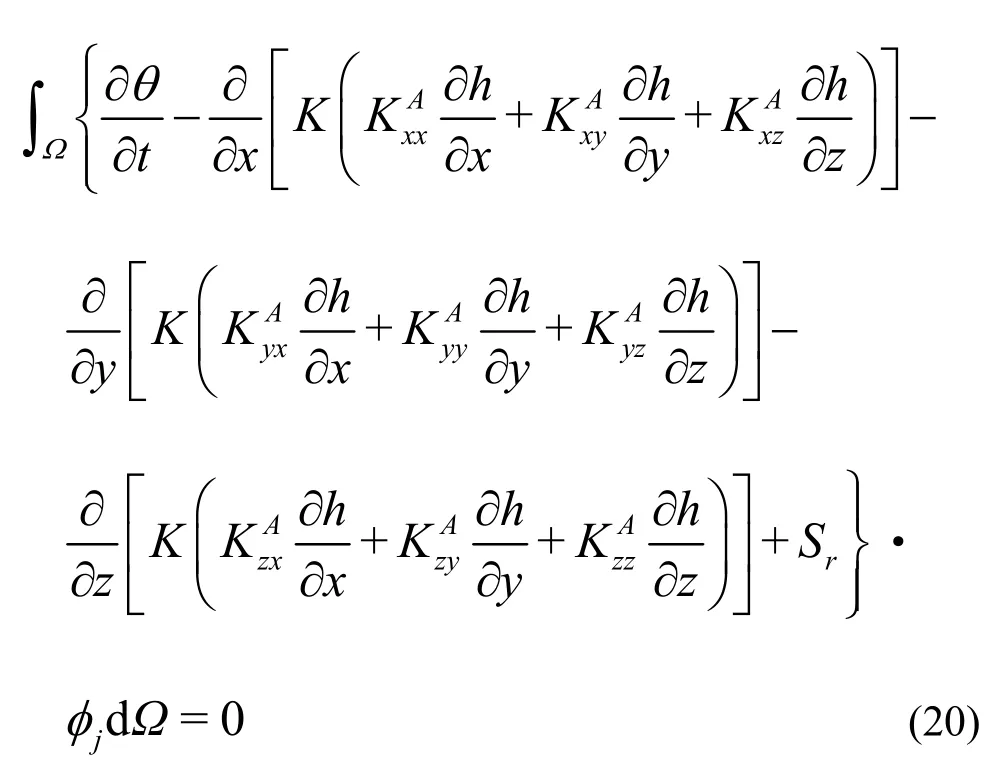
After replacing h byh, applying principle of partial integration, incorporating the Neumann type boundary condition and performing the integration over an element, Eq.(20) can be reduced to

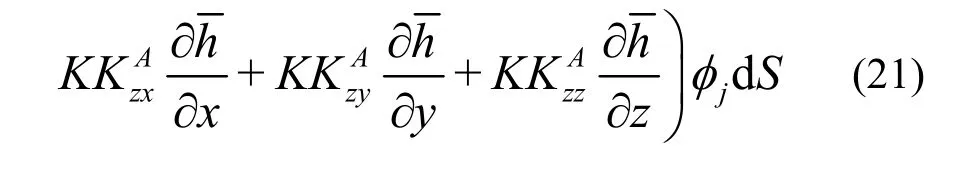
where Ωeis the area of an element, and Seis the boundary of the element. Substituting Eq.(19) into Eq.(21) and carrying out the integration lead to a set of ordinary differential equations in matrix form

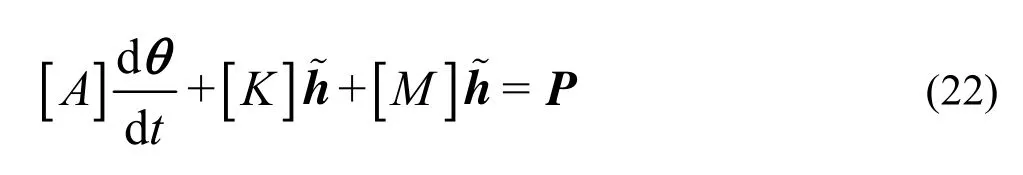
where θ and h~are respectively the vectors of water content and pressure head at the nodal points. The matrices[A], [K ], [M ] and the vector P are

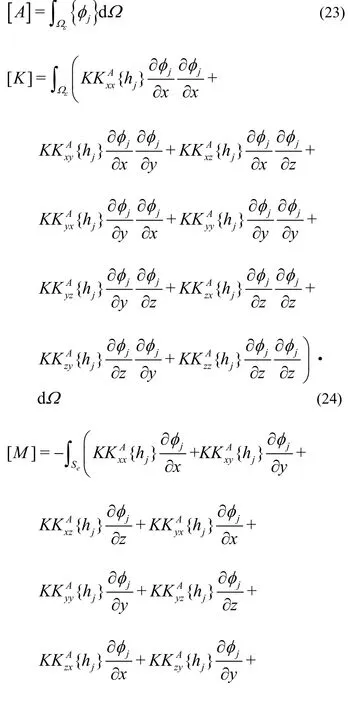
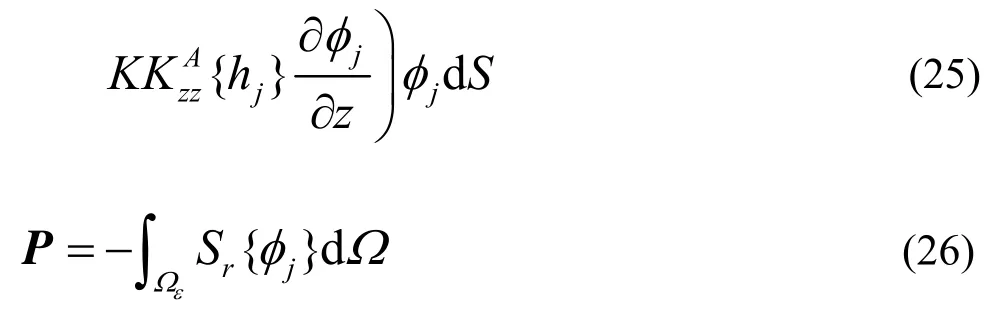
3.2 Finite element discretization for pollutant

transport

The concentration C( x, y, z, t ) of pollutantis is approximated by the functionC( x, y, z, t) in terms of the base function φ( x, y, z),

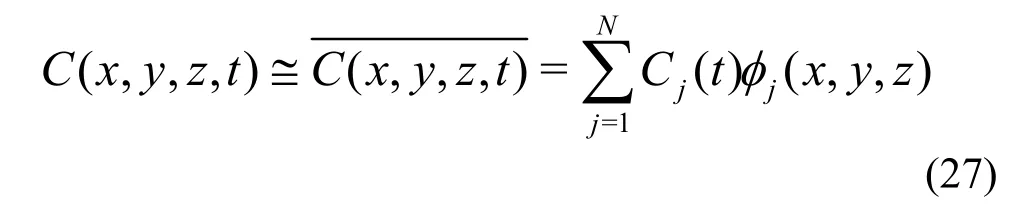
where φj(x, y, z) is the piecewise linear base function, which satisfies the essential boundary conditions, Cjthe nodal value of the C( x, y, z, t ) to be solved, and N the total number of nodes of the computational domain. On the basis of Eq.(27) and the principle of the Galerkin residual method, the Galerkin integral can be formulated as

In a similar procedure, Eq. (28) can be transformed into the time-dependant ordinary differential equation in the matrix form

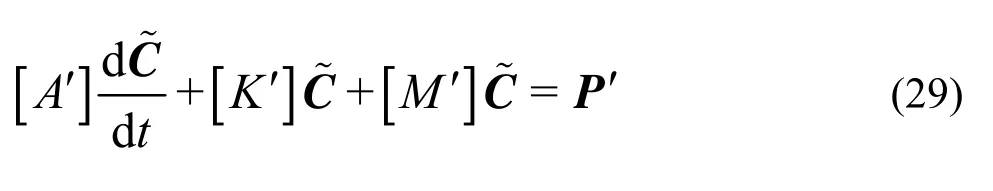
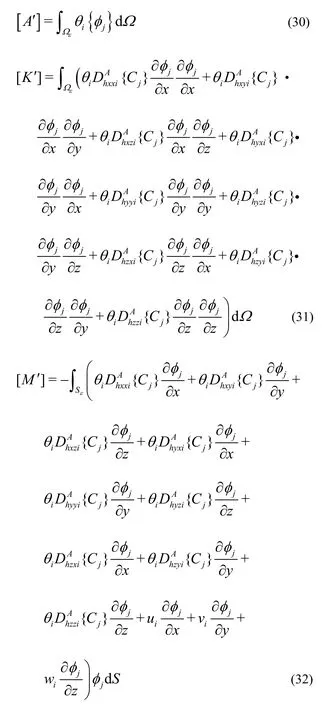
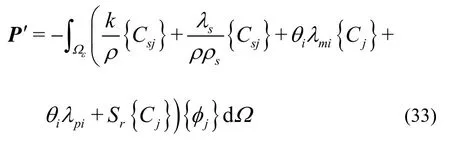
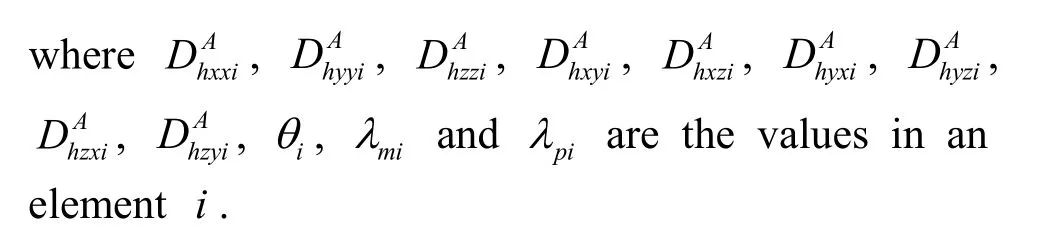
Fig.1 Experimental equipment

4. Application

4.1 Brief description of the experiment

The pot test had altogether 24 plastic pots. The pots were divided into eight groups, and each group included a blank sample and two parallel samples with two different plants for comparison. The pot was 0.53 m high, bottom diameter was 0.35 m, upper diameter was 0.405 m and the volume was 60 litres. The pots were filled with natural fine sand from the Nanjing section of the Yangtse River (its porosity was about 35%). The depth of the sand was 0.40 m while saturated zone was kept 0.26 m in depth, the depth of the sand was 0.49 m while saturated zone was kept 0.38 m in depth. A pipe with a valve was connected to the pot at the position 0.07 m above the bottom of the pot. The pipe was used for taking the water sample. The synthetic waste water was dropping into sand through the holes uniformly distributed in a circular pipe simulating uniform infiltration of the runoff, as shown in Fig.1. The Acorus calamus Linn and Arundo donax var. versicolor were planted in pots for testing the effects of the plants on the pollutant removal. The orthogonal method was used in designing the experiment. There were four levels of the hydraulic loading rate, two types of plants and two depths of the saturated zone chosen, and eight groups of experiments performed. The experiments were carried out in the summer and autumn, and the concentrations of water quality indexes CODCr, NH4+-N, TN and TP in the influent and effluent were measured. The experimental conditions of four case out listed in Table 1

Fig.2 Computational mesh of pot

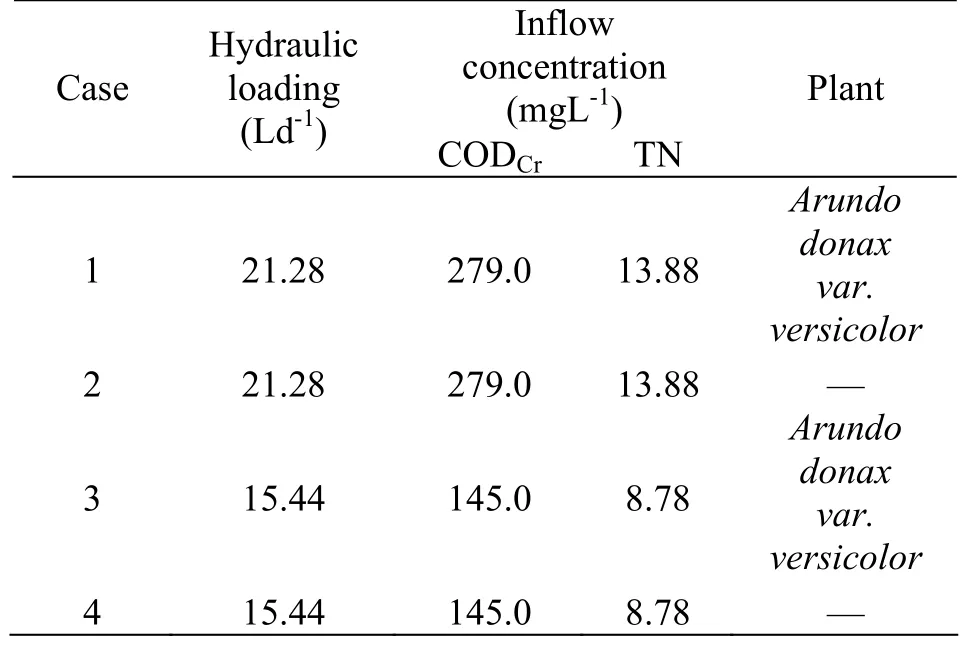
Table 1 Experimental condition

4.2 Computation of water movement and pollutant transport

4.2.1 Basic properties of material

The pots were filled with natural fine sand. The sand was assumed uniform and isotropic. The basic properties of the sand are given in the Table 2. The data in the table were from the experiments carried out in this study and from literature[22,23]. D50is the median size of the natural fine sand, anddρ is the density of the natural fine sand.

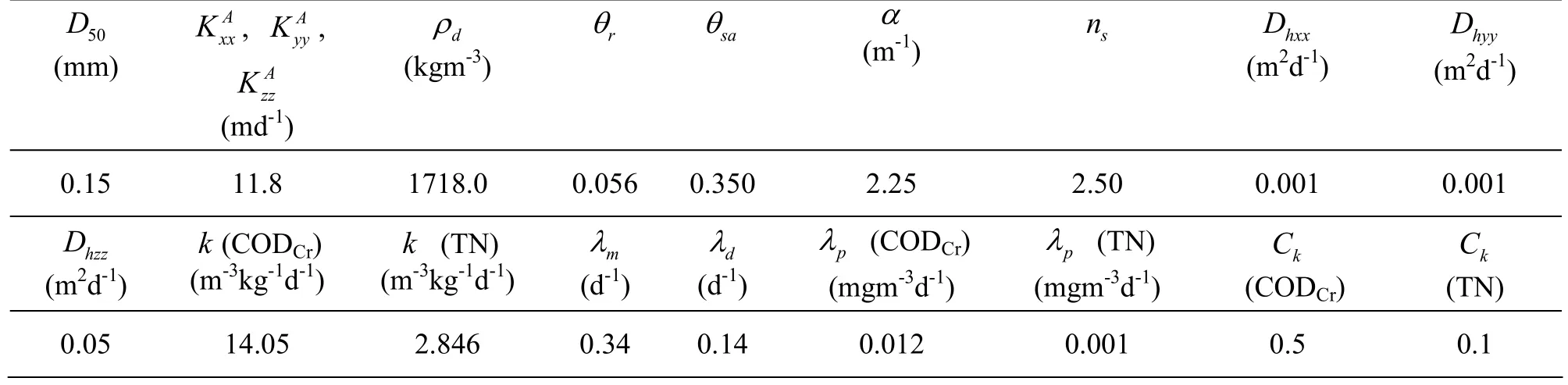
Table 2 Properties of the natural fine sand and the computational parameters

4.2.2 Computational mesh

The sand body was discretized with the tetrahedral element, as shown in Fig.2. The total nodes were 4 636 and the numbers of elements were 3 924.

4.2.3 Computational condition

The mathematical model was applied to the pot test, and four cases of experimental conditions were chosen to calculate. The experimental conditions of those four cases are listed in Table 1. The depth of the saturated zone was 0.38 m in all those cases.

The computational parameters used in the water movement calculation and pollutant transport calculation are summarized in Table 2. λdis the degradation coefficient of natural fine sand.

The initial conditions were given as: (1) h =0.38 ?z(n), for the pressure head at each node n, where z( n) was the elevation of the node n, and the datum of the z was at the bottom of the pot and upwards, (2) q=0, at each node, (3) CTN=CTNO, CCODCr=C(CODCr)O, CTNOand C(CODCr)Owere the background concentrations of the pollutants.

The boundary conditions were given as: (1) q=0at side wall and at bottom, (2) h =0.38 m, constant water head at the nodes representing the effluent sampling pipe, (3) the hydraulic loading and pollutant concentration at the top was determined according to Table 1. The hydraulic loading had the intermittent pattern to simulate the rainfall duration and the occurrence of frequency.

4.2.4 Computational results

The numerical results of the concentration of CODCrand TN in the effluent of four cases were compared with the experimental results, as shown in Figs.3 and 4. The black small circles were the experimental results. One example of the CODCrdistribution in the sand at time 0.3 d, 1.0 d, 3.0 d and 5 d after inflow is shown in Fig.5.

4.3 Discussion

The computed results of the pollutant concentrations in the effluent followed well with the main features of the experimental data, as shown in Figs.3 and 4. There exists discrepancy between the computed and measured data. This is mainly due tomeasuring error, especially when the concentration of the pollutant is relatively small, and the values of those parameters used in the computation do not accurately describe the real physical, chemical and biochemical processes.

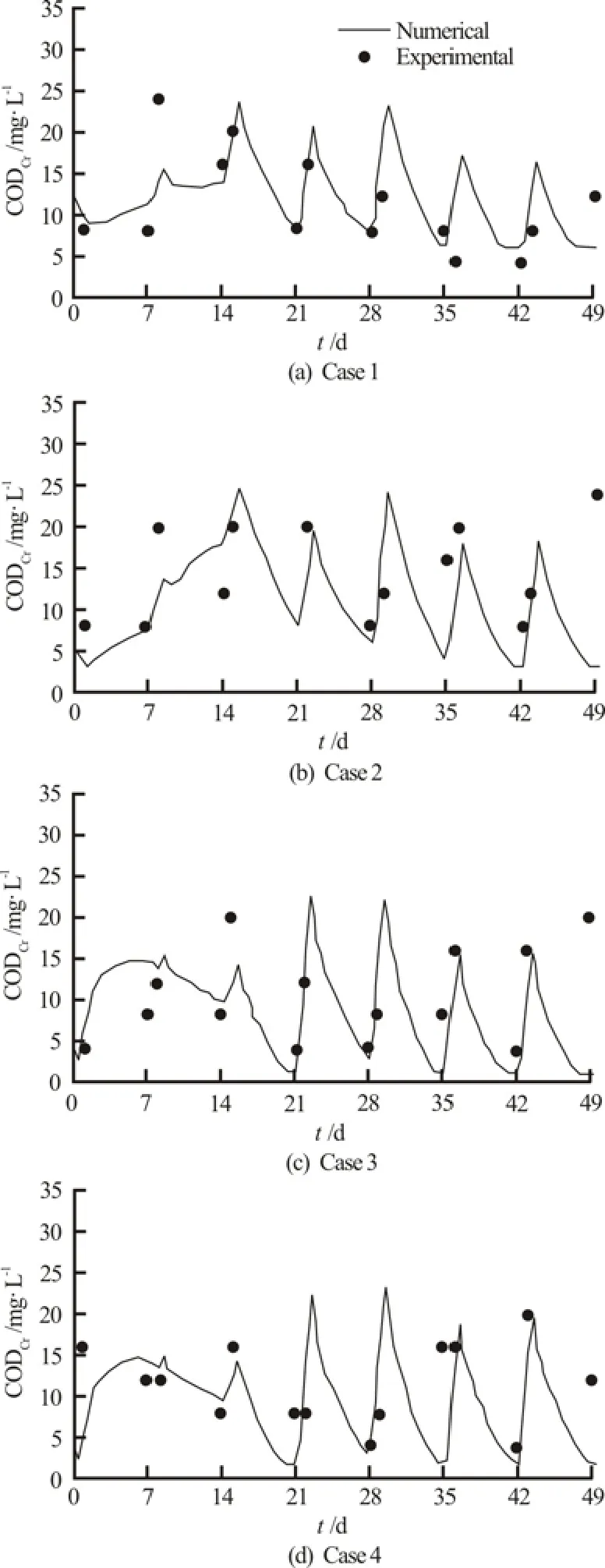
Fig.3 Comparison between numerical and experimental results for the concentration of CODCrin the effluent

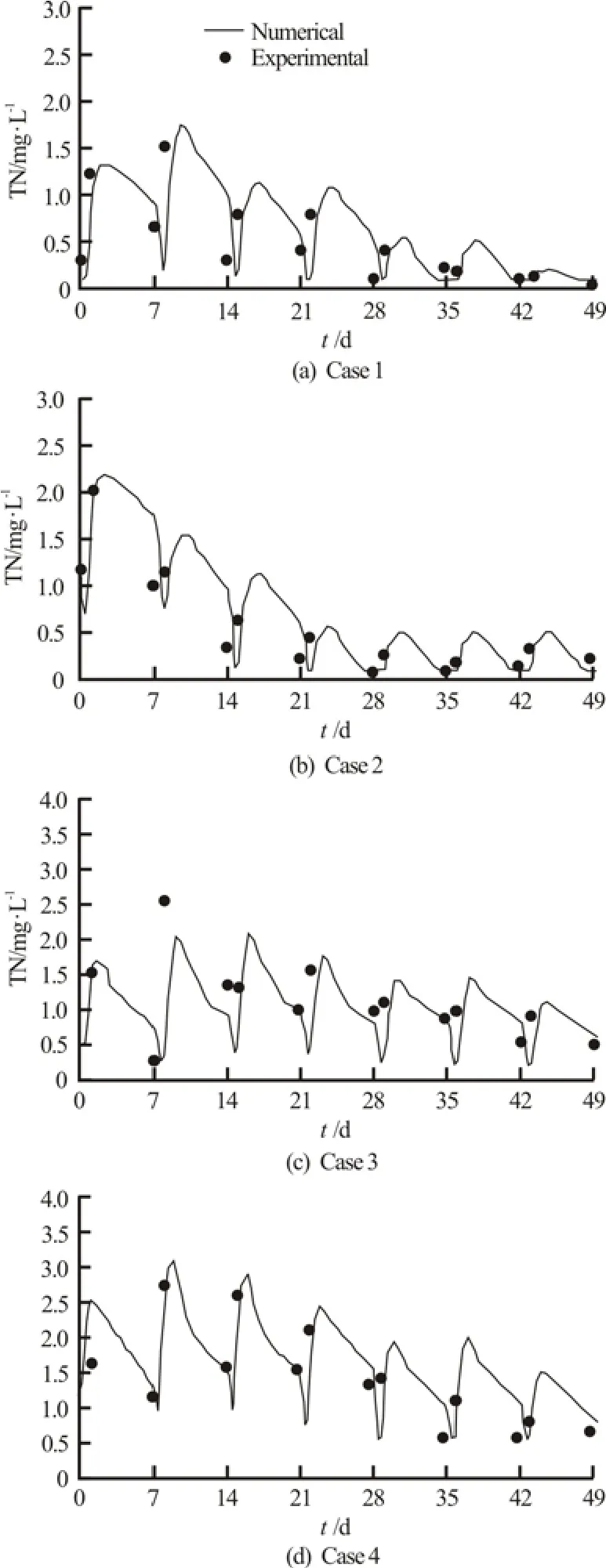
Fig.4 Comparison between numerical and experimental results for the concentration of TN in the effluent

The time varying pattern is caused by the intermittent pattern of the hydraulic loading. It could be seen clearly from Fig.5 that the pollutant is gradually transported and diffused from the influent points into the sand. The concentration of the pollutant is increasing during loading time and gradually decreasing after loading stopped.

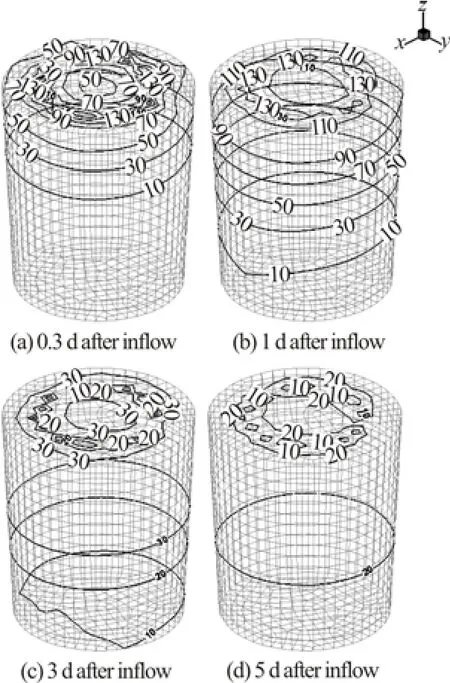
Fig.5 CODCrdistribution in the sand after inflow

The computed and tested overall removal rates of four cases are shown in Table 3, which is defined as the ratio of the difference between time-mean value of the pollutant concentrations in the influent and effluent to the time-mean value of the pollutant concentrations in the influent. It could be seen that the largest difference between the computed and tested value is 5%. This error is acceptable in practice.

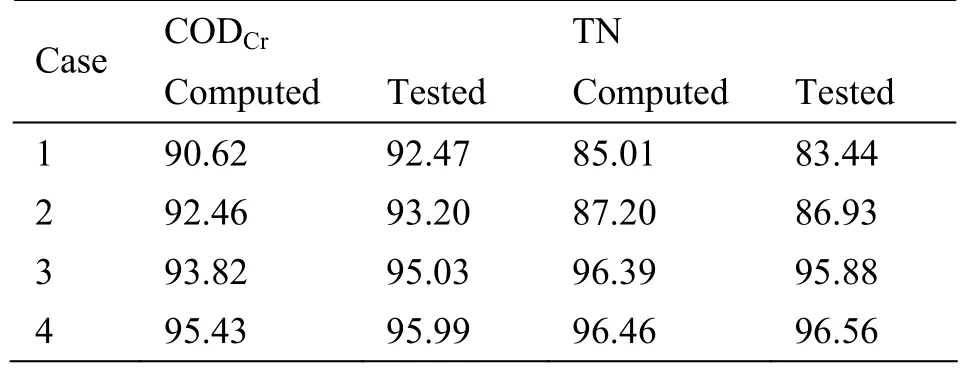
Table 3 Comparison of computed and tested overall removal rate (%)

5. Conclusion

A mathematical model has been developed in this study in order to simulate the pollutant removal behaviour of the pot test with and without plants. The results from the computation have been compared with the data from the pot tests. The tested overall removal rates for the CODCrand TN in four cases are in the range of 92.47% - 95.99% and 83.44% -96.56 %, respectively. The computed overall removal rates for the CODCrand TN in four cases are in the range of 90.62% - 95.43% and 85.01% - 96.46%, respectively. The differences between the computed and tested overall removal rates for the CODCrand TN are smaller than 5%. The time-varying oscillationpattern of the concentrations of the CODCrand TN has been rationally simulated. The capacity of the mathematical model in predication of the purification efficiency of those relevant devices is well validated. Of course, the model needs further improvement with more experimental data and field measurements.

Acknowledgement

This work was supported by the Natural Science Foundation of Hohai University (Grant No. 2008427511).

[1] MA Ying, RAJKUMAR M. and FREITAS H. Improvement of plant growth and nickel uptake by nickel resistant-plant-growth promoting bacteria[J]. Journal of Hazardous Materials, 2009, 166(2-3): 1154-1161.

[2] JAMALI M. K., KAZI T. G. and ARAIN M. B. et al. Heavy metal accumulation in different varieties of wheat (Triticum aestivum L.) grown in soil amended with domestic sewage sludge[J]. Journal of Hazardous Materials, 2009, 164(2-3): 1386-1391.

[3] MA Ying, RAJKUMAR M. and FREITAS H. Isolation and characterization of Ni mobilizing PGPB from serpentine soils and their potential in promoting plant growth and Ni accumulation by Brassica spp.[J]. Chemosphere, 2009, 75(6): 719-725.

[4] HARRIS J. N., NEW P. B. and MATIN P. M. Laboratory tests can predict beneficial effects of phosphate-solubilising bacteria on plants[J]. Soil Biology and Biochemistry, 2006, 38(7): 1521-1526.

[5] MIRANSARI M., BAHARAMI H. A. and REJALI F. et al. Effects of soil compaction and arbuscular mycorrhiza on corn (Zea mays L.) nutrient uptake[J]. Soil and Tillage Research, 2009, 103(2): 282-290.

[6] F?RSTER B., MUROYA K. and GARCIA M. Plant growth and microbial activity in a tropical soil amended with faecal pellets from millipedes and woodlice[J]. Pedobiologia, 2006, 50(3): 281-290.

[7] VOJTěCH L., LEP? J. Effect of functional group richness and species richness in manipulated productivity-diversity studies: A glasshouse pot experiment[J]. Acta Oecologica, 2006, 29(1): 85-96.

[8] GRACIANO C., GUIAMéT J. J. and GOYA J. F. Impact of nitrogen and phosphorus fertilization on drought responses in Eucalyptus grandis seedlings[J]. Forest Ecology and Management, 2005, 212(1-3): 40-49.

[9] PARADELO R., CENDóN Y. and MOLDES A. B. et al. A pot experiment with mixtures of slate processing fines and compost[J]. Geoderma, 2007, 141(3-4): 363-369.

[10] AHN C., MITSCH W. J. and WOLFE W. E. Effects of recycled FGD liner material on water quality and macrophytes of constructed wetlands: A mesocosm experiment[J]. Water Research, 2001, 35(3): 633-642.

[11] FRASER L. H., CARTY S. M. and STEER D. A test of four plant species to reduce total nitrogen and total phosphorus from soil leachate in subsurface wetland microcosms[J]. Bioresource Technology, 2004, 94(2): 185-192.

[12] HUNTER R. G., COMBS D. L. and GEORGE D. B. Nitrogen, phosphorous, and organic carbon removal in simulated wetland treatment systems[J]. Archives of Environmental Contamination and Toxicology, 2001, 41(3): 274-281.

[13] EPELDE L., MIJANGOS I. and BECERRIL J. M. et al. Soil microbial community as bioindicator of the recovery of soil functioning derived from metal phytoextraction with sorghum[J]. Soil Biology and Biochemistry, 2009, 41(9): 1788-1794.

[14] ASAEDA T., TRUNG V. K. and MANATUNGE J. et al. Modelling of macrophyte-nutrient-phytoplankton interactions in shallow eutrophic lakes and the evaluation of environmental impacts[J]. Ecological Engineering, 2001, 16(3): 341-357.

[15] van der PEIJL M. J., VERHOEVEN J. T. A. A model of carbon, nitrogen, and phosphorus dynamics and their interactions in river marginal wetlands[J]. Ecological Modelling, 1999, 118(2-3): 95-130.

[16] SPIELES D. J., MITSCH W. J. A model of macroinvertebrate trophic structure and oxygen demand in freshwater wetlands[J]. Ecological Modelling, 2003, 161(3): 181-192.

[17] YIN Hai-long, XU Zu-xin and LI Huai-zheng et al. Numerical modelling of wastewater transport and degradation in soil aquifer[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(5): 597-605.

[18] HUA Lei-na, YU Xi-ping. An enhanced element-free Galerkin method for dynamic response of poroelastic seabed[J]. Journal of Hydrodynamics, 2009, 21(3): 429-435.

[19] LUO Zu-jiang, ZHANG Ying-ying and WU Yong-xia. Finite element numerical simulation of three dimensional seepage control for deep foundation pit dewatering[J]. Journal of Hydrodynamics, 2008, 20(5): 596-602.

[20] ZHANG Qian-fei, LAN Shou-qi and WANG Yan-min et al. A new numerical method for groundwater flow and solute transport using velocity field[J]. Journal of Hydrodynamics, 2008, 20(3): 356-364.

[21] BRUN A., ENGESGAARD P. Modelling of transport and biogeochemical processes in pollution plumes: Literature review and model development[J]. Journal of Hydrology, 2002, 256(3-4): 211-227.

[22] DAI Yu, WANG De-guan. Numerical study on the purification performance of riverbank[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(5): 643-652.

[23] YAN Fei, ZHAN Mei-li and SU Bao-yu. Analysis on unsaturated seepage calculation parameter[J]. Journal of Yangtze River Scientific Research Institute, 2004, 21(5): 28-31(in Chinese).

10.1016/S1001-6058(09)60107-4

* Biography: DAI Yu (1979-), Female, Ph. D., Lecturer

WANG De-guan, E-mail: wangdeguan@hhu.edu.cn