Data-Based Filters for Non-Gaussian Dynamic Systems With Unknown Output Noise Covariance
Elham Javanfar and Mehdi Rahmani ,,
Abstract—This paper proposes linear and nonlinear filters for a non-Gaussian dynamic system with an unknown nominal covariance of the output noise.The challenge of designing a suitable filter in the presence of an unknown covariance matrix is addressed by focusing on the output data set of the system.Considering that data generated from a Gaussian distribution exhibit ellipsoidal scattering, we first propose the weighted sum of norms (SON)clustering method that prioritizes nearby points, reduces distant point influence, and lowers computational cost.Then, by introducing the weighted maximum likelihood, we propose a semi-definite program (SDP) to detect outliers and reduce their impacts on each cluster.Detecting these weights paves the way to obtain an appropriate covariance of the output noise.Next, two filtering approaches are presented: a cluster-based robust linear filter using the maximum a posterior (MAP) estimation and a clusterbased robust nonlinear filter assuming that output noise distribution stems from some Gaussian noise resources according to the ellipsoidal clusters.At last, simulation results demonstrate the effectiveness of our proposed filtering approaches.
I.INTRODUCTION
DUE to science and technology’s rapid advances, a significant number of data are being generated in various engineering fields, including but not limited to satellite-based remote sensors, time-series systems, and telecommunication data [1].This has made it imperative to analyze and process big data in contemporary engineering design, particularly in the areas of modeling, control, and estimation.
By appearing complex dynamics in different real-world systems such as robotics, aerospace, transportation, power grid,etc., we face significant uncertainties and less knowledge in our designs [2].In this regard, traditional methods and principles in controller design, system monitoring, and performance evaluation are challenging or infeasible.Most approaches depend on accurate physical and dynamic models and complete information about design parameters.Obtaining an exact model is hard or impossible for complex systems.Different methods to model systems can be involved in four main categories: analytical, numerical, data-driven, and hybrid models[3].In the era of machine learning, data-driven approaches offer powerful tools for identifying dynamical systems without requiring a deep understanding of the model structure[4], [5].
Data-based methods in dynamic systems have been presented primarily in control problems and rarely in state estimation.These methods play a crucial role in system identification and balancing the lack of knowledge about essential design parameters.During the last decades since the Industrial Revolution, system identification has been a critical element in most practical complex designs.Moreover, in some cases, despite access to the system model, many conventional estimation and control structures may not be applicable due to a lack of essential information.Recently, advancements in computational capabilities, iterative learning, reinforcement learning, and deep learning have given rise to new online and offline approaches to compensate for the problems mentioned above [6]-[9].
Estimation in dynamic systems is performed to obtain approximations of the system parameters using information from a model and any available measurements.Among all estimation and filtering methods, the Kalman filter is pervasive.It is a filter that uses the Bayesian rule to express the posterior probability in terms of the likelihood and the prior distributions [10].The classical Kalman filtering theory has two main assumptions.The first is the accuracy of prior knowledge of the system model and statistical noise features,and the second is the Gaussianity of noises.In many practical systems, noises are non-Gaussian due to environmental conditions, sensor failure, manufacturing activities, etc.Heavytailed noises are most important among these different kinds of noises [11], [12].Various filters have been designed to work out the filtering problem against heavy-tailed noises,e.g., see [13]-[18].Although these filters have suitable performance, they have limitations like knowing the accurate nominal relevant covariance matrices or comparative threshold.Since non-Gaussian heavy-tailed noises increase the covariance value of a distribution [19], filters need some considerations to compensate for it.Lack of exact models and essential knowledge about the system and noise features degrade the performance of filters; therefore, data-driven filtering methods are gaining popularity.In [20], a direct data-driven filter has been designed with no mathematical model for linear time-invariant dynamic systems with bounded disturbances and noises.The authors use set membership to estimate the sets of solutions.Furthermore, using quantized measurements,[21] proposes a data-driven filter to minimize the worst-case estimation error in the presence of bounded noises.Also, it introduces an L2- L∞approximately-optimal worst-case filter through linear programming technique.Recently, data-driven unknown input observer and state estimator for linear timeinvariant systems are investigated in [22].
Considering all of the mentioned points, data-driven techniques have not been effectively applied in state estimation problems.Moreover, despite having information about dynamic models, conventional filtering methods are sometimes inefficient because of severe environmental noise conditions and lack of statistical features.Generally, covariance matrix estimation methods can be divided into four major groups including correlation method [23], the maximum-likelihood method [24], the covariance matching method [25] and the Bayesian method [26].Unfortunately, not only do most of these approaches assume that noises have Gaussian distribution but also they suffer from some problems such as sensitivity to outliers, reaching non-invertible covariance matrices,etc.Therefore, there is a solid need to design an appropriate filter for dynamic systems in the presence of non-Gaussian noises with less or no information about noise covariances.For non-Gaussian systems, a finite set of higher-order moments of the state and measurement noises is obtained in[27] using the correlation measurement difference method,such that the observable matrix is full rank.Moreover, some recent works such as [28], [29] present a set of suitable filters against inaccurate covariances of the process and measurement noises for non-Gaussian dynamic systems using the variational Bayesian method.Since these filters are designed based on the probability density functions, they are more sensitive to initial values of distributions’ parameters.Considering all stated problems for obtaining noise covariance, using systems output data can be an effective way to compensate for deficit knowledge.This motivates us to propose a data-based filter for time-variant non-Gaussian systems without depending on the output nominal noise and accurate process noise covariances.In the proposed approach, we assume that system output data are accessible.
Grouping data based on their likeness is an approved concept in various science fields.In statistics, however, it can be done based on two different situations where there is prior information to gain more about the group structure or not.Unavailable information necessitates unsupervised learning tools or clustering algorithms.In other words, the problem of dividing a given set of data points with high uniformity within the groups and low diversity between groups is called clustering.Clustering is ubiquitous in machine learning, pattern recognition, statistics, image processing, and biology.Some important clustering algorithms are hierarchical clustering,Gaussian mixture models (GMMs), and K-mean clustering[30].Each of these methods bears some disadvantages.Time complexity and nonexisting mathematical objectives are primary defects of hierarchical clustering [31].Long computation time, falling into local optimum, and deciding are the dominant shortages of Gaussian mixture models [32], [33].Also, sensitivity to the initial condition and considerably different clustering results are the focal paucities of K-means clustering [34], [35].These methods are generally beset by local minima, which are sometimes significantly suboptimal.Recently, sum-of-norms (SON) clustering has been introduced that ensures a unique global minimizer [36], [37] and covers all the problems mentioned earlier.
Clustering the system data plays a vital role in our proposed filtering scheme.The shape representation of a cluster is also vital in preserving the data features.Ellipsoidal clusters are common because many data observations are normally distributed [38].We cluster the data using the sum-of-norms clustering method according to this characteristic and the above-discussed advantages.In this method, because of choosing a threshold value as a meter for Euclidian distances,each cluster may suffer from some outliers.This changes the ellipsoidal shape due to pushing the cluster center closer to the outliers.We propose a semi-definite program based on the weighted maximum likelihood estimation (MLE) to decrease their bad effects.By reducing the outlier’s effect, we find the robust covariance of each cluster as the covariance of output noise for data belonging to that cluster.Finally, we propose cluster-based linear and nonlinear filters.To sum it up, the goals and contributions of the proposed approach can be listed as follows.
1) To design a data-based filter against heavy-tailed noises with unknown output and inaccurate process noise covariance.
2) To present the idea of ellipsoidal clustering to compensate for less knowledge about noises’ statistical features.
3) To suggest the weighted SON clustering to improve regularization and the performance of the conventional SON.
4) To propose the weighted MLE to decrease the effect of outliers in each cluster and keep the clusters’ ellipsoidal shape.
5) To present two data-based filtering approaches, including cluster-based linear and cluster-based non-linear filters.
The remainder of the paper is organized as follows.Section II formally reviews some prerequisite and briefly refers to the main problem.The clustering steps, a new SDP to reduce the effects of outliers, and the proposed cluster-based filters are discussed in Section III.The notable specifications and features of the proposed filtering approaches are presented in Section IV.The simulation results are given in Section V before concluding the paper in Section VI.
Notations: The paper uses the following standard notations.Rmand Rm×rsignify them-dimensional Euclidean space and the set of allm×rreal matrices, respectively.N (·) designates the multivariate Gaussian probability density function.0 andI represent zero and identity matric∏es with appropriate dimensions, respectively.Furthermore, shows the product operation.The symbol “*” in matrices stands for the symmetric terms.Also, l og(·) indicates the natural logarithm operation.
II.PRELIMINARIES AND PROBLEM FORMULATION
The concepts listed below will be used to achieve our key goals.
A. Sum-of-Norms Clustering
We are interested in dividing a set of observations,Rd, into different clusters such that the close points to each other are assigned to the same cluster based on the Euclidian meter.We do not know the number of clusters, and it is unnecessary to be large.Assume that each cluster has a centroid in μjand is a subset of Rd.The SON clustering problem is presented as follows [37]:
in whichp≥1, and λ>0 can be regarded as a parameter that controls the trade-off between the first term in (1) and the number of clusters.The term ofpresents the sum-of-squares error, where μjis the centroid of the cluster containingxj.If the corresponding μ’s are the same, two differentx’s belong to the same cluster.This is the result of the second term in (1), which is a regularization term.In addition,we choosep=2 in the proposed approach, but other choices are possible.After finding the center of the clusters using the optimization problem (1), the data are fitted to each cluster based on the spatial threshold.
B. Multivariate Gaussian Distribution
The Gaussian distribution, also known as the normal distribution, resembles a symmetrical bell shape.Letxbe a random vector on Rp.It has the following probability density function:
where Ξ ∈Rp×pis the positive definite covariance matrix, andμis the mean.
Remark 1: (x-μ)TΞ-1(x-μ), is a square of Mahalanobis distance.It corresponds to the actual probability of the occurrence of the observation.
C. Maximum Likelihood Estimation
Maximum likelihood estimation is a popular way of obtaining practical estimators.Cramer Rao Lower Bound (CRLB),Gaussian PDF, and unbiasedness are among MLE’s asymptotic properties.Consider a set of i.i.d of data pointsY∈Rm×n,containingnobservations, which have a Gaussian distribution with mean μ and covariance Ξ.The likelihood function, under the normality assumption, can be written as
When dealing with large data sets, we frequently seek statistical and mathematical models to simplify their presentations.One of the first questions we ask is whether the data can be fitted with a normal distribution.This entails estimating the normal distribution’s mean and covariance.They are usually computed using the conventional MLE method by the following problem:
In this problem, the best estimates of the mean and variance are obtained by taking the partial derivative with respect toμand Ξ of the log-likelihood function and setting it to zero.As a result, we get
According to the normality condition, the log-likelihood function consists of the sum of the squared Mahalanobis distances.Consequently, if outlier data exist, the mean and covariance are pushed toward the outliers.
Remark 2: Maximizing the logarithm of the likelihood cost function is equivalent to minimizing the Mahalanobis distance.Outliers make the Mahalanobis distance large.
D. Kalman Filter
The Kalman filter is the most famous state estimator for linear Gaussian systems, but its performance is degraded in the presence of non-Gaussian noises.It can be derived from Bayesian recursive relations.In this regard, prediction and filtering steps are achieved as follows:
Prediction:
Filter:
where the gain matrix is given by
E. System Model
We assume that output measured data are produced from the following linear state-space dynamic model:
wherexk∈Rnxandyk∈Rnyare, respectively, the state and the measurement signals.Ak∈Rnx×nxandCk∈Rny×nxare dynamic and output matrices, respectively.Process noise,vk, is a non-Gaussian noise vector with zero mean and inaccurate nominal covariance,Qk.Also, measurement noise sequence,wk, is a non-Gaussian noise vector with zero mean and unknown nominal covariance matrix,Rk.It is remarkable that the process noise stems from internal factors while output noise comes from external sources; therefore, the process e xperiences less intense noise than the system’s output.Moreover, all measurements up to and including timekare presented by yk.We assume that the initial conditionx0and the system’s noises are mutually independent, satisfying the following relation:
wherexˉ0is the expectation ofx0.
This paper aims to design data-based filters for the output data set,y, produced by (9).It is assumed that the output noise nominal covariance is unknown.In the presence of outliers,conventional MLE estimators are affected by both good and bad observations.To compensate for this defect, after applying the proposed clustering method, we try to detect outliers in each cluster to decrease their effects on changing the shape of clusters and the covariances.Then, we present a linear filter based on the moving horizon estimation technique by restating the conventional MAP estimation problem for a measurement data set.Moreover, considering that data in each ellipsoidal cluster originated from a Gaussian distribution, we assume that there are εlellipsoidal clusters with Gaussian specifications for the output noise.By doing so, we propose a novel data-based nonlinear filter.
III.MAIN RESULTS
We intend to design a suitable filter for non-Gaussian linear dynamic systems with unknown output and inaccurate process noise covariance.Regarding our idea of output measurements clustering, first, we propose the weighted SON clustering method that improves the conventional SON’s performance in a large data set.
A. Weighted Sum-of-Norms Clustering
We propose the following weighted SON clustering to mitigate the influence of distances between cluster centers on the clustering performance and enhance the computational efficiency of the conventional SON clustering method (1):
where ζi j≥0 is a weighting parameter.
Using a constant weight for each point in the objective function of clustering can lead to suboptimal results because distant points with low similarity values would have the same impact as nearby points with high similarity values.To address this issue, we introduce the concept that the affinity weight, ζi j, quantifies the similarity betweenxjandxi, and assigns higher weights to nearby points and lower weights to distant ones.This approach can also reduce the impact of noise and outliers and consequently, result in more accurate and robust clustering.This requires that the weight ζi jbe obtained from a similarity function based on a statistical similarity measure criterion.The similarity function is typically a strictly monotonically decreasing continuous function in the[0 ∞)range with a positive second-order derivative.Remark 3: The similarity measure criterion provides freedom in selecting the similarity function.One of the most widely recognized functions is the Gaussian kernel.?
We know that the data in the same cluster have similar statistical features.Hence, to obtain output noise covariance,first, we decide to cover a set ofnpoints yk, by some ellipses(?1,?2,...,ε?)using the weighted SON clustering.Now, at the first step, Algorithm 1 is presented for clustering purpose.
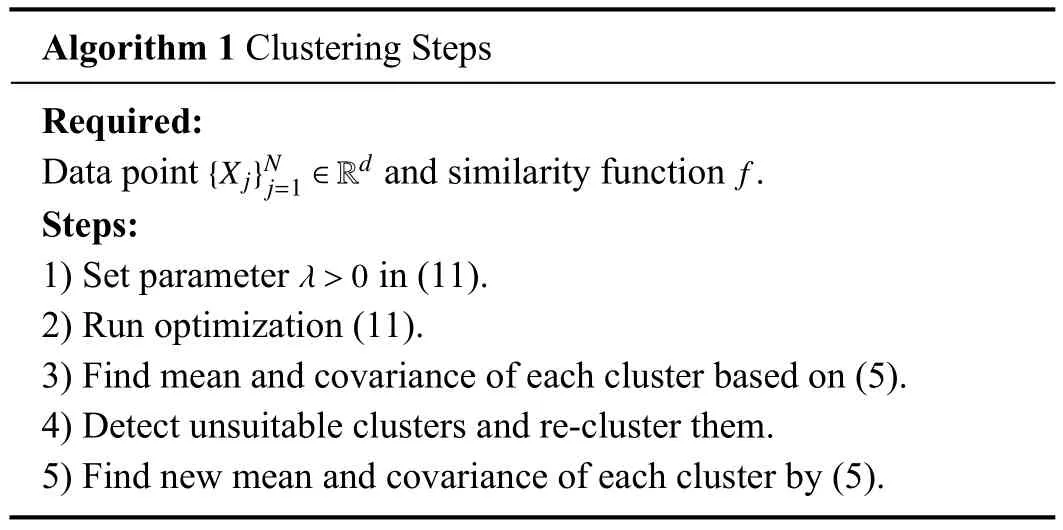
Algorithm 1 Clustering Steps Required:{X j}Nj=1 ∈Rd f Data point and similarity function.Steps:1) Set parameter in (11).2) Run optimization (11).3) Find mean and covariance of each cluster based on (5).4) Detect unsuitable clusters and re-cluster them.5) Find new mean and covariance of each cluster by (5).λ>0
Remark 4: To have more efficiency in Algorithm 1, a reclustering process is welcome for unsuitable clusters.In this regard, clusters with a small number of data are removed and combined with the other clusters, and clusters with large estimated covariances are divided into some smaller clusters.By doing so, a balance is made between the number of clusters and their number of data.
B. Detecting and Reducing the Effect of Outliers
The presented clustering algorithm results in some ellipsoidal clusters for output data of the system.According to the fact that Gaussian data have ellipsoidal scattering, we will encourage the use of the filters developed for Gaussian systems for each cluster.Note that the obtained clusters may suffer from some outlier data.Outliers can change the covariance of that cluster and create remarkable bias in the conventional MLE.For this reason, we are supposed to make a difference between outliers and good data to improve the performance of the MLE.In this regard, we need to minimize the sum of the smallest squared Mahalanobis distances while outliers with larger squared values are excluded.Under such a circumstance, we introduce a variable ωiin the range of [0 1],so that if the squared Mahalanobis distance is larger, the corresponding ωiis smaller.This approach is useful in state estimation to detect and decrease the effect of outliers.According to this concept, we consider the following weighted MLE:
We can rewrite the cost function in (12) by replacing the likelihood function (3) and using the features of the logarithm function as follows:
One crucial point is that the above log-likelihood function is not concave or convex.
If we fix the parameter ω in the optimization problem (12),we can easily obtain the mean and covariance variables by the following lemma.
Lemma 1: Consider the weighted MLE problem (12), the mean and covariance, μ and Ξ, are obtained by
Proof: By taking partial derivations of (12) with respect toμand Ξ and setting them tos zero, it is straightforward to obtain(14).
Due to a lack of knowledge of good and bad observations and the problem’s non-convexity, we cannot determine the appropriate weights and utilize the weighted MLE.Iterative algorithms, like iteratively reweighted least squares [39], can solve this problem by updating the weights in inverse proportion to Mahalanobis distances.However, slow convergence and trap into local optimal solutions are some of their weaknesses.In the following, with the help of a suitable objective function and introducing probability criterion on all observations, we will present an optimization problem to set the outliers with smaller weights for solving the above-mentioned issues.To this end, considering the following relations:
and using the fact that outliers have low probability and large Mahalanobis distances, we encourage using probability of occurrence as weights to decrease the effect of outliers in our proposed method.We introduce a positive weight vectorwithTherefore, inspiring Remark 2, the mean and covariances of the weighted MLE (14), and the squared Mahalanobis distances (15), we present the following optimization problem to obtain optimal values ofχ andd:
In (16), the loss function must be monotonically nondecreasing function of χianddi.This function should be chosen such that χiis inversely proportional to the corresponding Mahalanobis distance,di.Doing so allows all outlier observations with largedito receive small weight χi.On the other hand, we ought to choose a suitable cost function such that the sum of all Mahalanobis distances is small.To satisfy all of these conditions, in the optimization problem (16), we propose the cost function as
In what follows, we present a theorem to obtain the best values of weights, χi, which have an essential role in outliers detection and decreasing their effects.
Theorem 1: The optimization problem (16) with the cost function (17) can be reformulated as the following SDP problem:
Proof:For the cost function (17), assume an upper bound,δi, such that.Thus, minimization of this cost can be formulated as follows:
The first constraint can be reformulated as
Now, by substituting the weighted mean and covariance from the constraints of (16), the above equation can be simplified as
Finally, applying the Schur complement equivalence, the SDP problem in (18) is obtained.■
Remark 5: Since outliers are destructive in different domains and applications and cause some limitations, the proposed SDP problem in (18) can detect outliers in each Gaussian data set without needing extra designs.
Until now, we have presented a method to cluster the data set and an optimization problem to compute the weights in the MLE for reducing the effect of outliers.Note that we can obtain the covariance of each cluster using two methods, the conventional MLE and the weighted MLE.The second method is robust against outliers thanks to obtaining the covariance according to reducing their impact.Now, we are ready to introduce our proposed filtering approaches.
C. Cluster-Based Linear Filter
Since the proposed approach incorporates the new weighted SON clustering and the new weighted MLE, we deal with a data set belonging to Gaussian distributions with different statistical features in each cluster.Given this circumstance, in this section, instead of using the existing recursive filters, such as the Kalman filter, to estimate or predict the states according to the available information at each instant, we intend to estimate the entire states at once using the whole data set.
Theorem 2: The state estimations for the output data set,y1:N, belonging to the system (9), can be obtained as
where
Proof: Based on the Bayesian method and using the fact that process and measurement noises are independent, we have
Thus, the posterior is given by
By rearranging the terms in (23) and using the defined matrices in (21), the optimization problem (22) can be written as
Consequently, taking partial derivation with respect to X,the estimation, X?, in (21) is obtained.
Since (21) involves the inverse of the matrix (O?TO?), this matrix grows in size as the number of data or dimension increases.To solve this unfavorable issue, we propose the following optimization problem to obtain the moving horizon estimation (MHE) with a window length ofNw:
Consequently, the steps of the proposed cluster-based robust moving horizon estimation are presented in Algorithm 2.
Remark 6: In Algorithm 2, Theorem 1 determines the best weights and detects outliers; subsequently, the elimination of outliers when computing the robust covariance matrices of each cluster results in a filter that is robust against outliers.Therefore, we call it a cluster-based robust MHE.We have a simple (non-robust) cluster-based MHE if we omit step 2 and determine the covariance matrix by the conventional MLE.

Algorithm 2 Cluster-Based Robust Moving Horizon Estimation Required:{X j}Nj=1 ∈Rd Nw Data Point and window length.Steps:1) Run Algorithm 1.2) Detect outliers of each cluster using Theorem 1.3) Calculate robust covariance matrix of each cluster.yk 4) Determine cluster of each.5) Obtain the state estimation from (25).
Remark 7: Equation (21) is the closed-form solution of the optimization problem (25) in a complete intervalNw=N.
D. Cluster-Based Non-Linear Filter
As we discussed, each ellipsoidal set’s data originates from a Gaussian distribution in the SON clustering.Since we cluster the output data with εlindependent ellipsoidal set and considering this assumption that the intensity of the process noise is less than output noise, we can assume that there existεlGaussian resources for the output noise distribution.Considering all clusters, the total occurrence probability of the output noise is equal to the sum of the occurrence probability of each Gaussian resource.This is another idea to design a new filter.We show that this filter would be non-linear.To this end, we introduce the following probability density function for each noise resource:

Using above explanations and substituting (27) into the Bayesian rule result in
The denominator in (28) involves the integration of the sum of likelihoods and priors for each noise distribution.This ensures that the total probability of all states ofx0giveny0equals one.In this vein, the density function (28) can be written as (29).

For simplicity, we assume
Using the Bayesian rule to inspire the strides of obtaining the Kalman filter, and after setting out the results, the proposed filter structure consists of the prediction and filtering steps as follows:
Prediction:
Filter:
Moreover, the filter gain can be obtained as
Now, after computing the estimation of each cluster, to obtain the unique estimation for the state,k, we have
Moreover, using (35) and (36), covariances of estimation error,Pkand, are given by
and
According to the main filter’s relation (35), this filtering approach consists of a bank of εlKalman filters.Although the prediction and filtering relations in (31), (32) and (33) are linear similar to the Kalman filter, because of using the nonlinear parameters ζkiand αkiin (33) for obtaining state estimationx?kin (35), the proposed filter in this part is nonlinear.
As the last step, Algorithm 3 is presented for the proposed cluster-based robust nonlinear filter.We have a simple cluster-based nonlinear filter by removing the second step in Algorithm 3 and using the conventional MLE.

Algorithm 3 Cluster-Based Robust Non-Linear Filter Required:{X j}Nj=1 ∈Rd εl Data Point and.Steps:1) Run Algorithm 1.2) Detect outliers of each cluster using Theorem 1.3) Calculate robust covariance matrix of each cluster.k ←1 for to N do? ←1 εl for to do 5) Compute the parameters in the prediction and filtering steps from (32) and (33).end for 6) Obtain the state estimation by (35).end for
IV.DISCUSSION ON THE RESULTS
In the development of filters, a bias in the estimate can arise due to heavy-tailed noises.To compensate for this bias, the effects of outliers should be reduced.Based on the above concepts, our proposed cluster-based robust filters have a better performance thanthe proposedcluster-basedfilters,dueto decreasing thefiltergain (34) andthe matrix F?in (21)which consequently improves the filter performance.However, various factors can affect the performance of moving horizon estimators such as window length, initial state, covariance values in the beginning of window, time-variant or time-invariant characteristics of the systems’ dynamic, etc.In light of the points mentioned above, we cannot explicitly claim which of the proposed filters is the best.
The impact of removing outliers (from a cluster or data set)on statistical covariance can vary depending on the distribution of the remaining data.The covariance decreases significantly when the outliers are large and far from the other data.These outliers can lead to significant variability and distortion in the covariance estimate.On the other hand, outliers consistent with the general trend of the data have different impacts on covariance if removed.It should be noted that the number of data in each cluster can also affect this phenomenon.
The number of measurement data in this process depends on the system complexity, dispersion, and constraints.Although clustering is possible for small number of data, the accuracy of covariance estimation and consequently, the precision of filtering decreases.Besides, highly dispersed data set are unreliable for clustering, while excessive data leads to a single ellipsoidal cluster due to the central limit theorem.Therefore,we suggest to check the data scatter and collect the measurement data such that the dispersion and empty positions are minimized in the whole data set.
In the proposed methods, different parameters appear in the optimization problem, filtering, and clustering.The parameters in the first and second groups are computed precisely.However, in the weighted SON clustering problem, the weights ζi jare obtained using the similarity functions.In Remark 3, the Gaussian kernel has been introduced as one of the most famous functions.Also,pis another parameter and determines which norm is used in the clustering.We know that different norms emphasize different aspects of the data,leading to variations in the clustering outcome.The proposed approach optimally uses the Euclidean norm (p=2) to capture the overall distance between data points without any bias or focusing on specific characteristic of data.
The proposed filtering algorithms are offline; therefore, they do not depend on the time properties of dynamic systems, i.e.,our proposed data-based filters can be applied to both timevariant and time-invariant systems.
V.SIMULATION STUDY
In this section, we want to study the performance and effectiveness of the proposed filters, including cluster-based MHE(C-B MHE), cluster-based robust MHE (C-B RMHE), clusterbased non-linear filter (C-B NF), and cluster-based robust non-linear filter (C-B RNF).For this purpose, we exert these filters on the time-varying and practical system subject to heavy-tailed noises.Since no completely related filters exist in the literature, we compare our proposed filters with those designed for non-Gaussian systems with known parameters.
A. Example 1: Three-Tank System
We consider a three-tank system with the schematic shown in Fig.1.The dynamics of this system can be described as follows:
whereQ1andQ2are the flow rates of pumps 1 and 2,qLiis the leakage flow rate of the tanki(i=1,2,3),hiis the level of the tanki,Acdenotes the cross-sectional area of the connecting pipe, andqmn(m≠n) is the flow rate from tankmto tankn.Parameters of the system and their numerical values are tabulated in Table I.

Fig.1.Three-tank system.

TABLE ITHREE-TANK SYSTEM PARAMETERS
Using the system parameters in Table I with operating points (Q1=5.5×10-5,Q2=3.4×10-5m3/s), and (h1=0.4,h2=0.23,h3=0.31m), and after linearization and discretization of the model (39), we reach the state space model of the system with the following matrices:
Process and measurement noises are non-Gaussian with the following distributions:
whereQ=R=0.035.
The performance of the proposed filters is compared to the maximum correntropy Kalman filter (MCKF) [13] as a famous filter in the presence of heavy-tailed noises, the conventionalMHEwithwindowlengthNw=10,and the conventionalKalmanfilter.Sincethe dimensionofthe matrixO?in(21) is extensive, to have more analysis, we introduce clusterbased and cluster-based robust Kalman filters using the conventional Kalman filter with estimated covariance matrix using MLE and weighted MLE, respectively.Fig.2 shows different filters’ state estimation and MSE.Our proposed databased filters perform better than the Kalman filter, the MCKF,and the conventional MHE designed with known and true parameters.The main reason for this deficiency is that the Kalman filter is a minimum mean square filter and is sensitive to non-Gaussian noises; therefore, its performance degrades against these noises.Also, as a prior filter against non-Gaussian noises, the maximum correntropy Kalman filter cannot guarantee a compelling performance against these noises.Moreover, although the conventional MHE uses data in a window to obtain estimations and has a weak performance against non-Gaussian noises, it outperforms the conventional Kalman filter and MCKF.This fact brings about the proposed cluster-based MHE and the proposed cluster-based robust MHE has a better response than the cluster-based Kalman filter and cluster-based robust Kalman filter.In contrast, data clustering, outlier detection, and data-based filtering equip the proposed approaches to perform well against non-Gaussian noises.
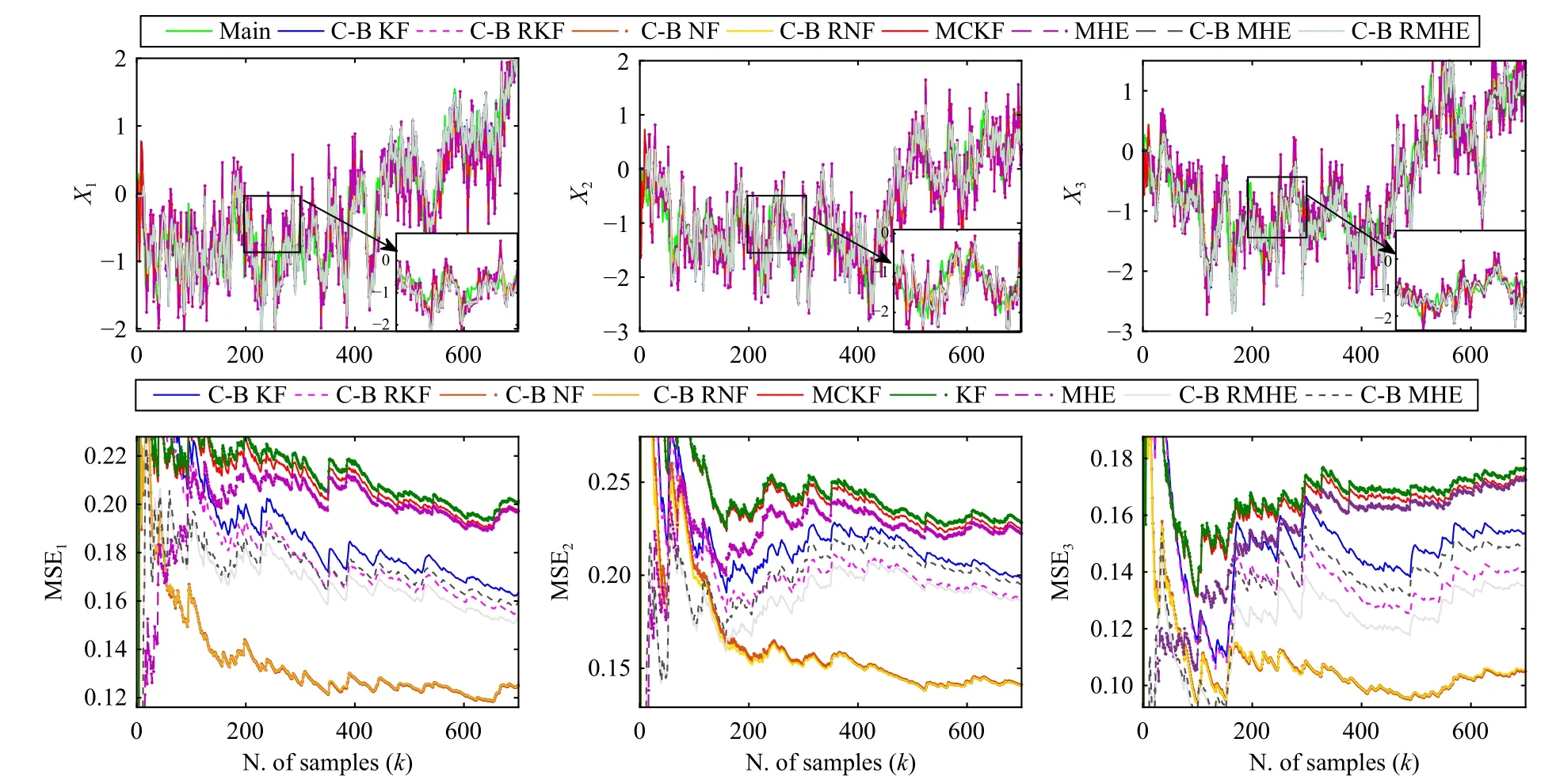
Fig.2.State estimations and MSEs in Example 1 (C-B, R, and N are abbreviation of cluster-based, robust, and non-linear).
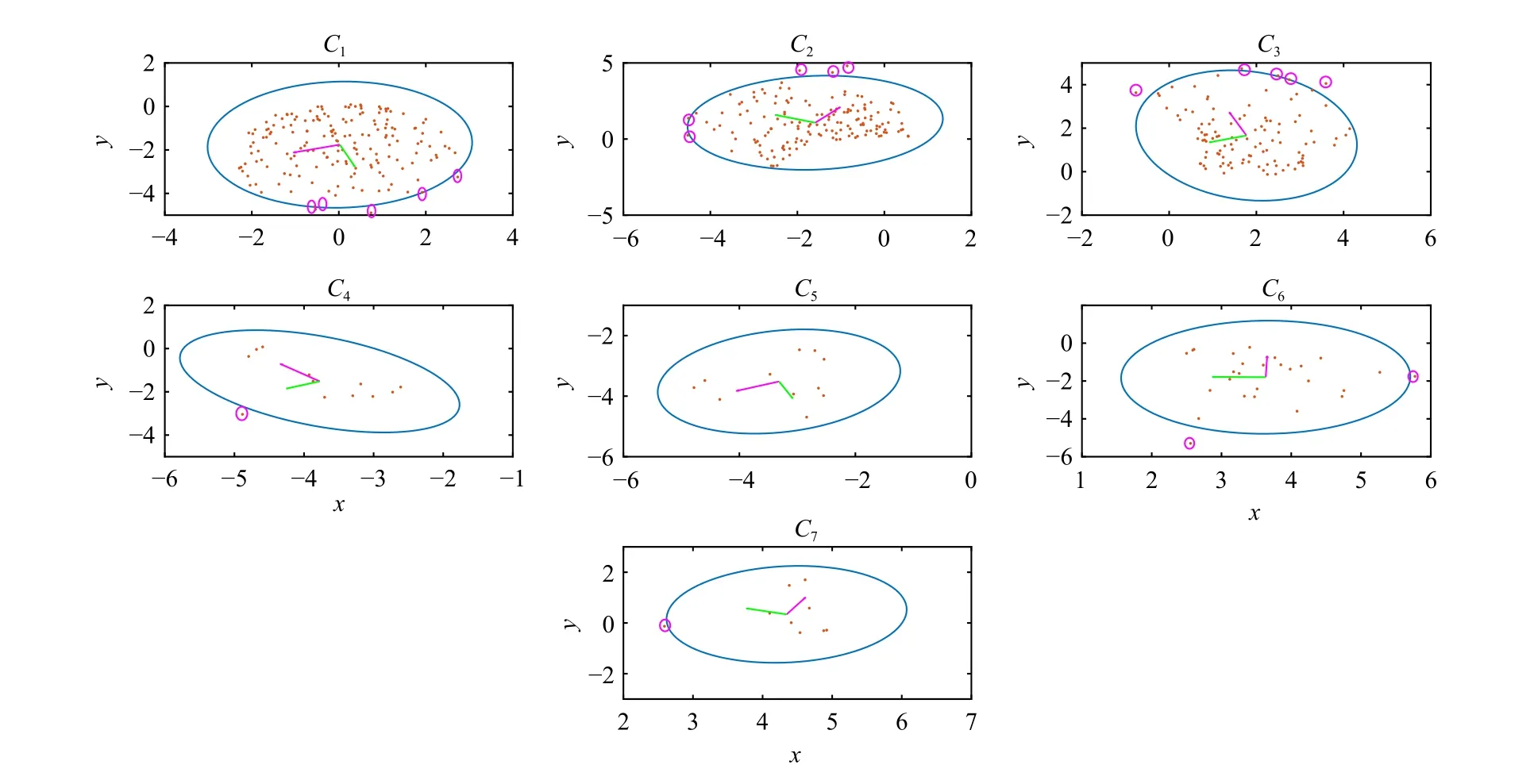
Fig.3.Error ellipse (Iso-Contour) of the each cluster with outliers in Example 2.
B. Example 2: Time-Variant System
To show the usefulness of our proposed filters for time-variant systems, we assume that output data set of the following non-Gaussian time-variant system (taken from [40] with some modification) are available:
Process and measurement noises are non-Gaussian with the
following distributions:
whereQ=R=0.15.
We have six ellipsoidal clusters after running Algorithm 1.Fig.3 shows the iso-contour of these six ellipsoidal clusters along with the outliers of each cluster.Clusters’ shapes without outliers emphasize the proposed optimization’s proper performance.It is worth noting that if the axes of ellipsoidal are parallel to coordinate axes, the obtained covariances are diagonal.Moreover, the results of mean square error of states for the proposed data-based filters are compared in Table II.Likewise, our proposed filters have better performance than the others.
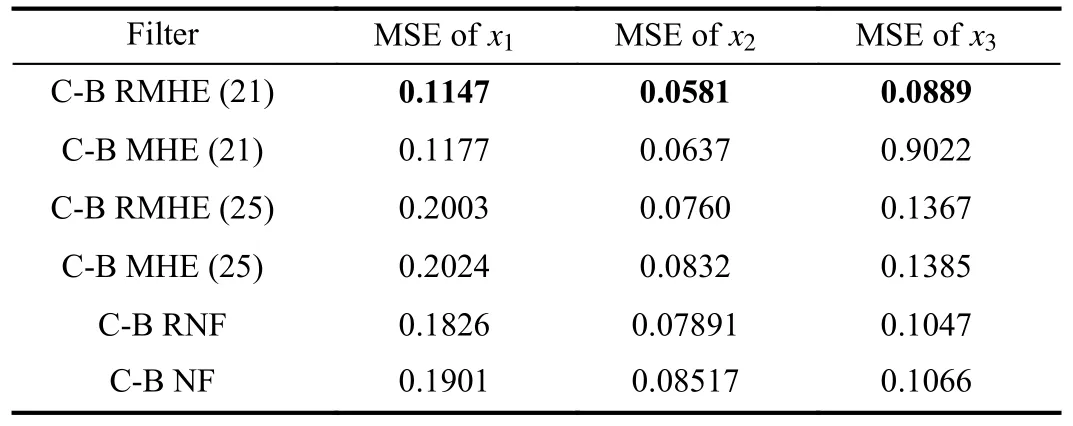
TABLE II MEAN SQUARE ERROR OF DIFFERENT FILTERS FOR NOISES IN (43)
Based on the results in Table II, the robust moving horizon estimation with a whole window performs better than other methods.This phenomenon is because MHE with a large window length in slow varying dynamic systems can capture more relevant information for estimation, and consequently,has a more reliable performance.
VI.CONCLUSION
In this paper, we aimed to develop data-based filters for linear dynamic systems against non-Gaussian heavy-tailed noises under the unknown output noise covariance condition.Inspiring that Gaussian data sets have ellipsoidal scattering, we clustered the output data set of a non-Gaussian dynamic system using the proposed weighted SON clustering method.The proposed approach can improve the performance of the SON clustering method by focusing on closely spaced points and reducing the computational cost.Outliers in each cluster can change the clusters’ ellipsoidal shape and affect the filter’s performance.To address this issue, we proposed an SDP problem based on the weighted maximum likelihood to detect outliers in each cluster and obtain a robust covariance matrix.We then developed four different filters using two approaches.In the first method, we presented the cluster-based MHE.Provided that output noise covariance is computed by the conventional MLE and the proposed SDP problem, we have a simple cluster-based filter and a robust cluster-based filter, respectively.In the second approach, given εlclusters, we assumed that there are εlGaussian resources for the output noise distribution with their specific statistician features.This idea led us to extract a non-linear filter structure, presenting a clusterbased non-linear filter and a cluster-based robust non-linear filter, depending on how the covariance matrix is computed.Finally, we verified the performance of our proposed filters through simulation results on a practical system and a timevariant system.
 IEEE/CAA Journal of Automatica Sinica2024年4期
IEEE/CAA Journal of Automatica Sinica2024年4期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Parameter-Free Shifted Laplacian Reconstruction for Multiple Kernel Clustering
- A Novel Trajectory Tracking Control of AGV Based on Udwadia-Kalaba Approach
- Attack-Resilient Distributed Cooperative Control of Virtually Coupled High-Speed Trains via Topology Reconfiguration
- Synchronization of Drive-Response Networks With Delays on Time Scales
- Policy Gradient Adaptive Dynamic Programming for Model-Free Multi-Objective Optimal Control
- Lyapunov Conditions for Finite-Time Input-to-State Stability of Impulsive Switched Systems
