THE BOUNDEDNESS OF OPERATORS ON WEIGHTED MULTI-PARAMETER LOCAL HARDY SPACES*
(丁衛(wèi)) (湯彥)
School of Sciences, Nantong University, Nantong 226007, China E-mail: dingwei@ntu.edu.cn; 994585863@qq.com
Yueping ZHU (朱月萍)?
Department of Mathematics, Nantong Normal College, Nantong 226010, China E-mail: zhuyueping@ntu.edu.cn
Abstract Though atomic decomposition is a very useful tool for studying the boundedness on Hardy spaces for some sublinear operators, untill now, the boundedness of operators on weighted Hardy spaces in a multi-parameter setting has been established only by almost orthogonality estimates.In this paper, we mainly establish the boundedness on weighted multi-parameter local Hardy spaces via atomic decomposition.
Key words weighted multi-parameter local Hardy spaces; atomic decomposition; boundedness; inhomogeneous Journ′e class
1 Introduction
The study of Hardy spaces can be traced back to the work of Hardy, who studied the behavior of holomorphic functions on the unit disk in 1915 [31].Since then, the theory of Hardy spaces has been extensively studied.We refer readers to the works [1-3, 33, 39-41].
In recent decades, the theory of multi-parameter Hardy spaces has been the subject of extensive studied.Gundy and Stein studied the product Hardy space on the polydisc in [26].After that, Chang and Fefferman developed this theory in [6-8].More recently, using discrete Calder′on’s identity, Han, Lu and Zhao proved in [30] that product Hardy space can also be characterised by discrete Littlewood-Paley square functions.In addition,the authors of[17,36,37] studied weighted multi-parameter Hardy spaces.For more results about multi-parameter Hardy spaces, we refer readers to [4, 5, 9, 11, 13, 14, 17-19, 22, 23, 26-29, 34-36, 38].
Following in these footsteps,multi-parameter local Hardy spaces have been studied recently in [14, 15].To be more precise, fori=1,2, letψ,ψ(i)∈S(Rni) with

where the series converges inL2(Rn1+n2),S(Rn1+n2) andS′(Rn1+n2).
Using (1.5), the multi-parameter local Hardy spaceshp(Rn1×Rn2) were introduced in [15]as follows:

when (x1,x2) is outside the support of functionf, where the kernelKsatisfies that, for fixedx1,y1∈Rn1, setting ~K1(x1,y1) as the singular integral operator acting on functions on Rn2

The smallest such constantCis denoted by‖K‖CZ.The norm of the operatorTis defined by‖T‖CZ=‖T‖L2→L2+‖K‖CZ.
In this paper, on the basis of [14], we study the boundedness of operators on the weighted multi-parameter Hardy spaces via atomic decomposition.For this purpose, we now recall some definitions of product weights in a two parameter setting[24].For 1<p <∞,a weight function,a nonnegative locally integrable function,ω ∈Ap(Rn1×Rn2) if there exists a constantC >0 such that
for any dyadic cuboidR=I×Jon Rn1×Rn2, that is,IandJare cubes on Rn1and Rn2,respectively.We say thatω ∈A1(Rn1×Rn2) if there exists a constantC >0 such that
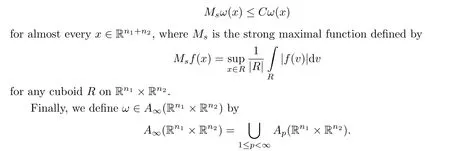
Ifω ∈A∞, thenqω=inf{q:ω ∈Aq}is called the critical index ofω.Notice that ifω ∈A∞,thenqω <∞.In this paper, we useAp(Rn) to denote the classical Muckenhoupt’s weights on Rn.
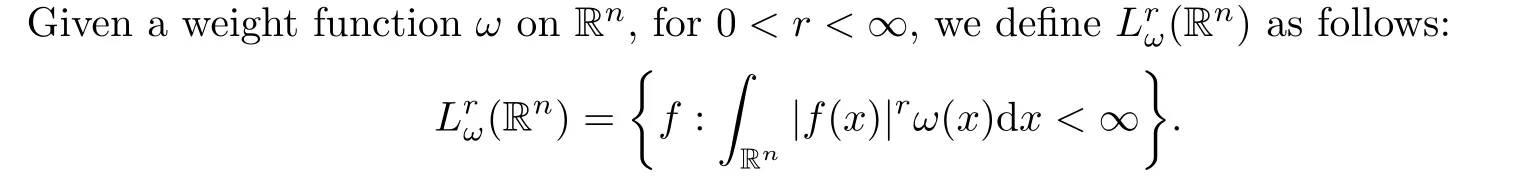
With the discrete Calde′ons identity (1.5), the following weighted multi-parameter local Hardy spaces were introduced in [12, 32]:
Definition 1.2 Let 0<p <∞andω ∈A∞(Rn1×Rn2).Suppose that, fori=1,2,ψ(i)0andψ(i)∈S(Rni)are functions satisfying conditions(1.1)-(1.3).The weighted multi-parameter local Hardy spacehpω(Rn1×Rn2) is defined by
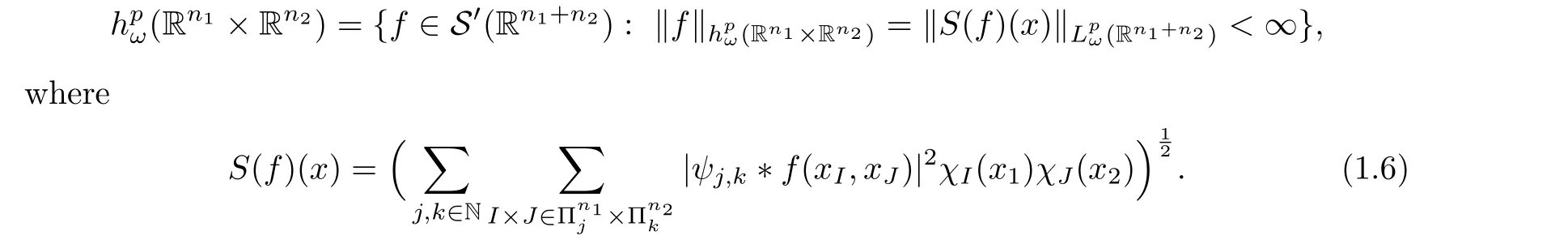
By the discrete local Calder′on’s identity (1.5), using a standard process, one can obtain that the weighted multi-parameter local Hardy spaces are well defined, that is,hpω(Rn1×Rn2)is independent of the test functions.
It is universally known that the atomic decomposition is very useful for investigating the boundedness on Hardy spaces for some sublinear operators in classical Hardy space theory.Untill now, the boundedness of operators on weighted multi-parameter Hardy spaces was established by almost orthogonality estimates [17, 28, 36, 37].However all of these proofs cannot be applied to operators in the Journ′e class.Recently, the atomic decomposition theorem for weighted multi-parameter local Hardy spaces was established in [12].Based on this, we study the boundedness on weighted multi-parameter local Hardy spaces of operators in the inhomogeneous Journ′e class via atomic decomposition.
We first recall the definition of atoms of weighted multi-parameter local Hardy spaces in[12].
Definition 1.3 Let 0<p ≤1 andω ∈A2(Rn1×Rn2).Anhpω(Rn1×Rn2) atom is a functiona(x1,x2) supported in an open set Ω?Rn1+n2satisfying that
Moveover,acan be further decomposed into some rectangle-atomsaRassociated with the rectangleR=I×Jwhich are supported inτRfor some positive integerτ >1 independent ofaandaR, and such that
with
whereM(Ω) is the set of all dyadic rectangles in Ω which are maximal in both directions ofx1andx2.Moreover, there exists a positive constant?, for rectangle-atomsaRassociated with the rectangleR=I×Jso that one has that
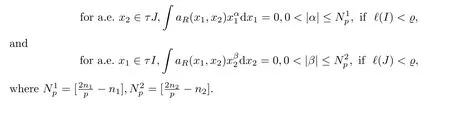

We want to point out that the boundedness of operators in a mixed Journ′e class on weighted multi-parameter mixed Hardy spaces was studied in [16], but that additional vanishing conditions on operators were assumed in order to ensure the use of almost orthogonality estimates.
The organization of the rest of this paper is as follows: in Section 2, we prove the uniform boundedness of atoms on weighted multi-parameter local Hardy spaces.In Section 3,we discuss the boundedness fromhpω(Rn1×Rn2) toLpω(Rn1+n2) of operators in an inhomogeneous Journ′e class.The proofs of Theorems 1.4 and 1.5 in this paper are more complicated than those without weights given in [14, 15].
Finally, we establish some conventions.Throughout the paper,Cdenotes a positive constant that is independent of the main parameters involved, but whose value may vary from line to line.Constants with a subscript, such asC1, do not change in different occurrences.We denotef ≤Cgbyf?g.Iff?g?f, we writef ≈g.
2 Uniform Boundedness of Atoms
Due to the existence of weights, the method used to prove the uniform boundedness of atoms in [14] cannot be applied to the case of a weighted multi-parameter setting.Thus, we follow the argument in[42].Generally,one uses a continuous Littlewood-Paley characterization to prove the uniform boundedness of atoms on multi-parameter Hardy spaces [14].In order to do this, the following equivalent relationship should first be established [12]:
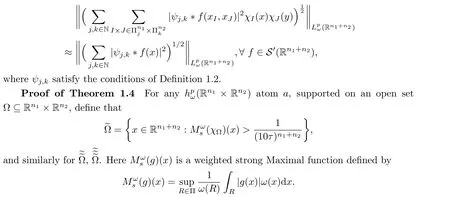

According to side length ofR, there are four cases: Case 1,?(I)<?,?(J)<?; Case 2,?(I)<?,?(J)≥?; Case 3,?(I)≥?,?(J)<?; Case 4,?(I)≥?,?(J)≥?.We claim that, in all cases,
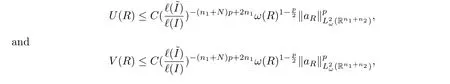


whereM(1)is the Hardy-Littlewood maximal operator inx1.By H¨older’s inequality and theL2boundedness with a weight ofM(1), one has that
Thus,

since?(I)≥?,?(J)≥?.In a fashion similar to the process for Case 2, one can obtain the estimates ofV(R).This proves the claim.Similarly, one can prove that
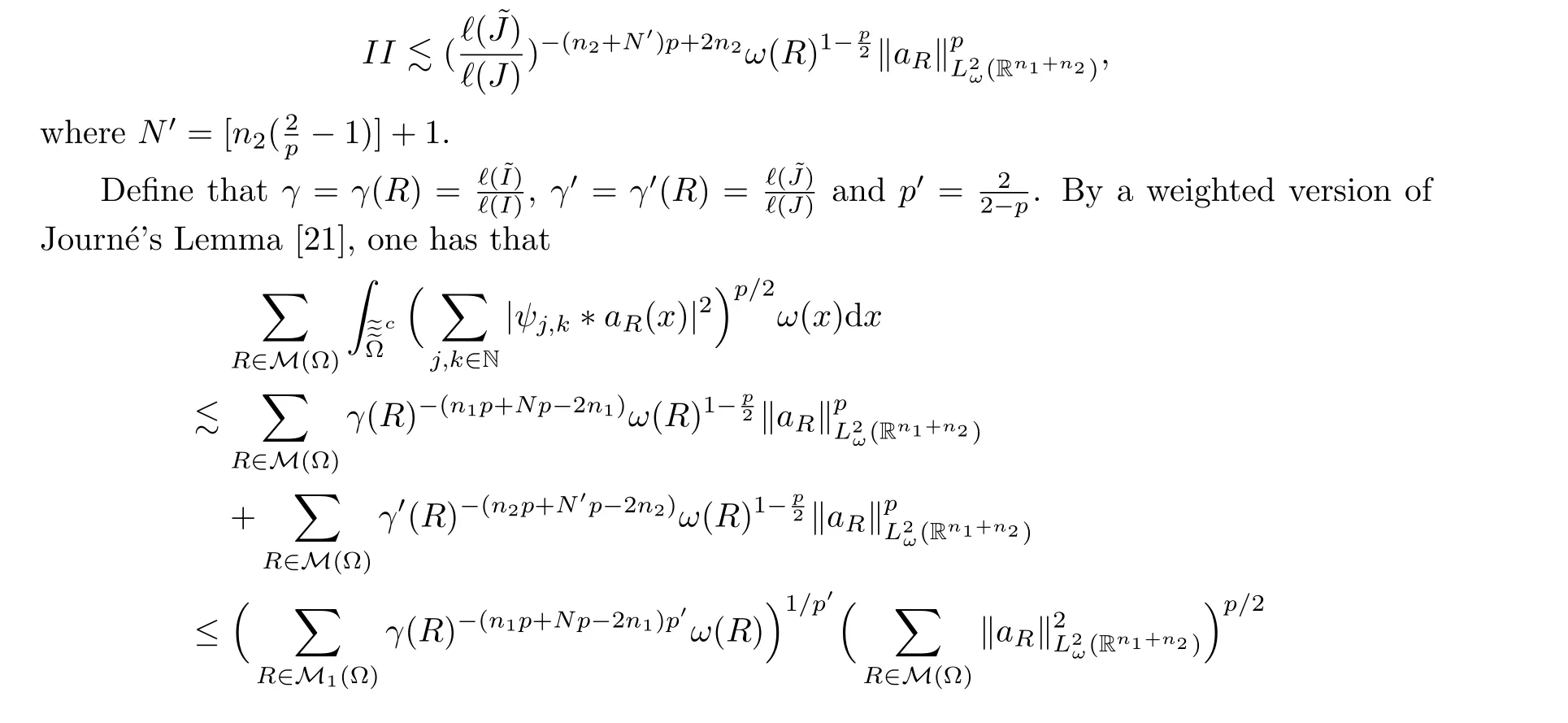
This finishes the proof.□
3 Boundedness of Operators
In this section,we establish the boundedness of operators in an inhomogeneous Journ′e class on weighted multi-parameter local Hardy spaces.Before this, we present some propositions about these spaces.First, similarly as to Proposition 3.1 in [16], we can obtain the dense class ofhpω(Rn1×Rn2).
Proposition 3.1Lettingω ∈A∞(Rn1×Rn2),S(Rn1+n2) is dense inhpω(Rn1×Rn2) for all 0<p <∞.
SinceS(Rn1+n2)?L2ω(Rn1+n2), one has the following result:
Corollary 3.2Suppose thatω ∈A∞(Rn1×Rn2).ThenL2ω(Rn1+n2)∩hpω(Rn1×Rn2) is dense inhpω(Rn1×Rn2) for all 0<p <∞.
The following atomic decomposition result is crucial to proving Theorem 1.5.

Proposition 3.3 was given in [12], and its proof is similar as that of Theorem 1.7 in [15].For the integrity of this article, we will sketch the proof in the Appendix.
To prove Theorem 1.5, we follow the approach of Fefferman in [21].This is similar to the process of proving Theorem 1.6 in [14] in terms of form, but is much more complicated.


whereε′= min{ε,δ}.For this, according to side length ofR, we discuss four cases: Case 1,?(I)≥?,?(J)≥?; Case 2,?(I)<?,?(J)≥?; Case 3,?(I)≥?,?(J)<?; Case 4,?(I)<?,?(J)<?.
For Case 1,?(I)≥?,?(J)≥?, we first discussU(R).Becausex ∈(10τ~I)c×(10τJ)c,
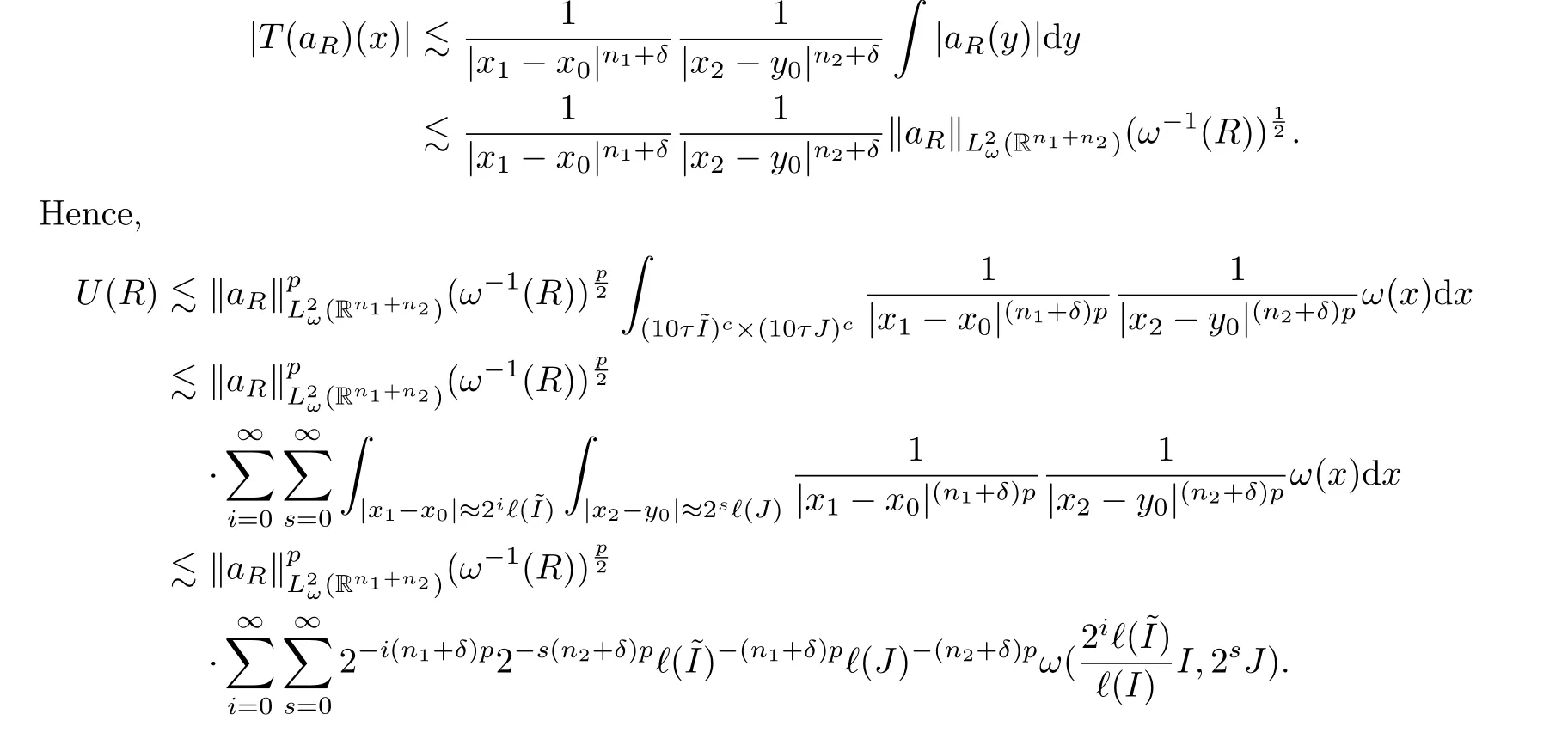

Now we follow the approach of Fefferman in [21]and use#2to denote the sharp operator in thex2variable.Then
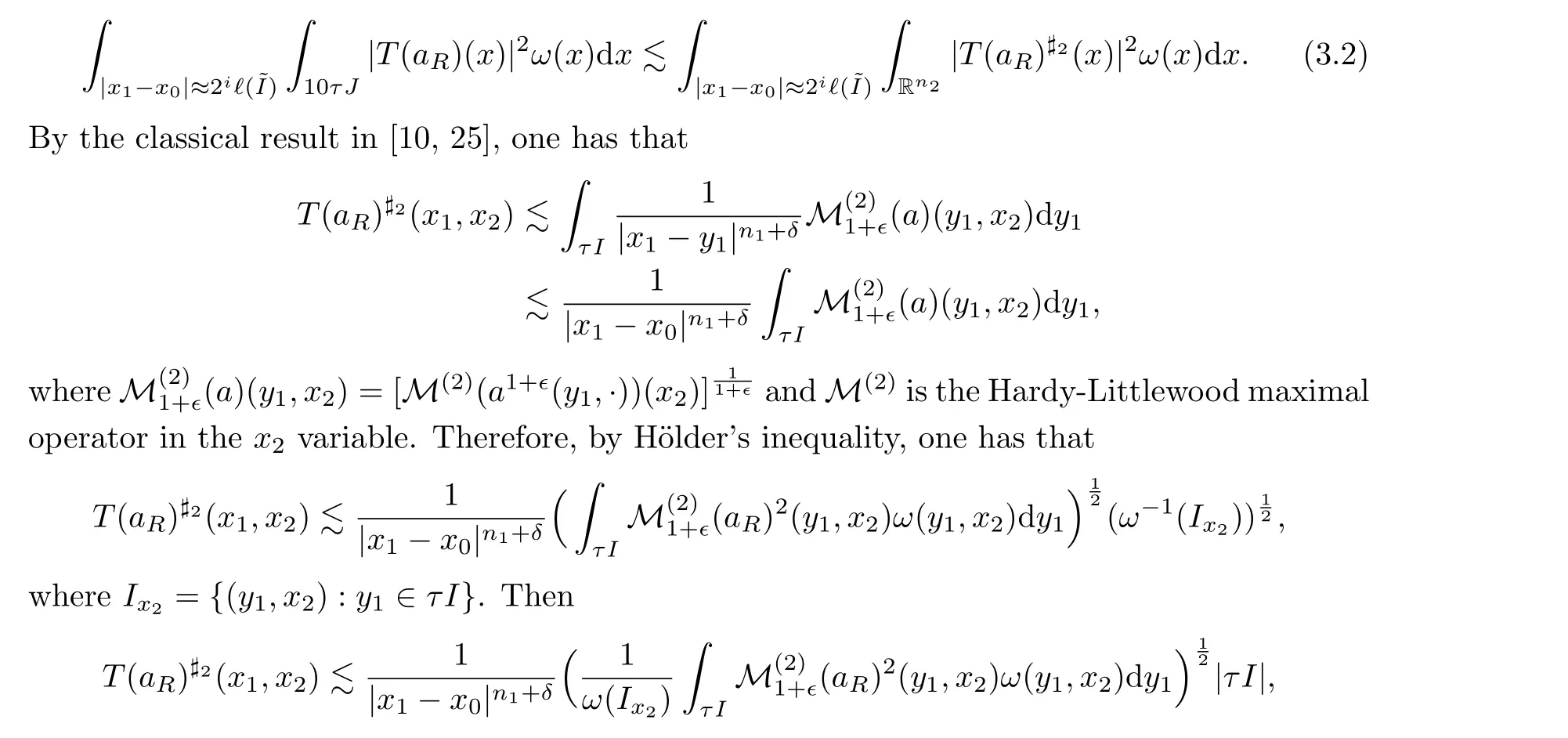

provided thatn1p+δp-qn1>0.
For Case 2,?(I)<?,?(J)≥?, first, using the cancellation condition ofaRin Rn1, we have that
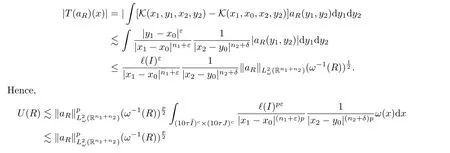

provided thatn1p+εp-qn1>0.
For Case 3, with a process similar to that for Case 2, one has that
provided that (n1+δ)p-qn1>0.
For Case 4, using the cancellation conditions ofaRinx1andx2, one has that

provided that (n2+ε′)p-qn2>0.
Finally, in a fashion similar to that for the estimates (2.1), we complete the proof.□
Conflict of InterestThe authors declare no conflict of interest.
Appendix


 Acta Mathematica Scientia(English Series)2024年1期
Acta Mathematica Scientia(English Series)2024年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*
- AGGREGATE SPECIAL FUNCTIONS TO APPROXIMATE PERMUTING TRI-HOMOMORPHISMS AND PERMUTING TRI-DERIVATIONS ASSOCIATED WITH A TRI-ADDITIVE ψ-FUNCTIONAL INEQUALITY IN BANACH ALGEBRAS*
- INTERFACE BEHAVIOR AND DECAY RATES OF COMPRESSIBLE NAVIER-STOKES SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND A VACUUM*
- CONVEXITY OF THE FREE BOUNDARY FOR AN AXISYMMETRIC INCOMPRESSIBLE IMPINGING JET*
- SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*
- COMPLETE K¨AHLER METRICS WITH POSITIVE HOLOMORPHIC SECTIONAL CURVATURES ON CERTAIN LINE BUNDLES (RELATED TO A COHOMOGENEITY ONE POINT OF VIEW ON A YAU CONJECTURE)*
