AGGREGATE SPECIAL FUNCTIONS TO APPROXIMATE PERMUTING TRI-HOMOMORPHISMS AND PERMUTING TRI-DERIVATIONS ASSOCIATED WITH A TRI-ADDITIVE ψ-FUNCTIONAL INEQUALITY IN BANACH ALGEBRAS*
Safoura Rezaei ADERYANI Azam AHADI Reza SAADATI
School of Mathematics, Iran University of Science and Technology, Narmak, Tehran, Iran E-mail: safora.rezaei.2000@gmail.com; azamahadi9710@gmail.com; rsaadati@eml.cc
Hari M. SRIVASTAVA
Department of Mathematics and Statistics, Universtity of Victoria, Canada;
Department of Medical Research, China Medical University Hospital, China Medical University,
Taichung 40402, China;
Department of Mathematics and Informatics, Azerbaijan University, 71 Jeyhun Hajibeyli Street,
AZ1007 Baku, Azerbaijan;
Section of Mathematics, International Telematic, University Uninettuno, I-00186 Rome, Italy E-mail: harimsri@math.uvic.ca
Abstract In this paper,we define a new class of control functions through aggregate special functions.These class of control functions help us to stabilize and approximate a tri-additive ψ-functional inequality to get a better estimation for permuting tri-homomorphisms and permuting tri-derivations in unital C*-algebras and Banach algebras by the vector-valued alternative fixed point theorem.
Key words permuting tri-homomorphism in Banach algebra; permuting tri-derivation on C*-algebra; fixed point theorem; Ulam-Hyers-Rassias stability; aggregate special functions; tri-additive ψ-functional inequality
1 Introduction and Preliminaries
Aggregation functions play a significant role in many of the technological tasks scientists are faced with nowadays.They are specifically significant in many problems related to the fusion of information.More generally, aggregation functions are widely used in applied mathematics(e.g., statistics, probability, decision mathematics), pure mathematics (e.g., theory of means and averages, functional equations, measure and integration theory), economics and finance(e.g., voting theory, game theory, decision making), computer and engineering sciences (e.g.,artificial intelligence, information theory, pattern recognition and image analysis, data fusion,operations research, engineering design, automated reasoning), social sciences(e.g., mathematical psychology, representational measurement) as well as many other applied fields of physics and natural sciences.Thus, a main characteristic of the aggregation functions is that they are used in a large number of areas and disciplines.The essence of aggregation is that the output value computed by the aggregation function should represent or synthesize in some sense all individual inputs, where quotes are put to emphasize the fact that the precise meaning of this expression is highly dependent on the context.In any case, defining or choosing the right class of aggregation functions for a specific problem is a difficult task, considering the huge variety of potential aggregation functions [1-4].
The central problem we are investigating in this paper is that of aggregation, which refers to the process of combining and merging several(most often numerical)values into a single one.Perhaps the oldest example in this respect is the notion of arithmetic mean or average, which has been used during all the history of physics and all experimental sciences.Any function like the arithmetic mean computing a single output value from an (arbitrarily long) vector of input values is called an aggregation function.
Here,we define a new class of control functions through aggregate special functions to investigate the Ulam-Hyers-Rassias stability [5] of the following tri-additiveψ-functional inequality
which was given by Park [6, 7] in complex Banach spaces by a method derived from vectorvalued alternative fixed point theorem.In addition, we study permuting tri-homomorphisms and permuting tri-derivations in unitalC*-algebras and Banach algebras associated with the tri-additiveψ-functional inequality (1.1).
Definition 1.1([8]) Suppose M is a ring.Permuting tri-derivation is a tri-additive mapping Z:M3→M satisfying
for all Ψ1,Ψ2,Ψ3,Ψ4,Φ1,Φ2,Φ3∈M and for any permutation (δ(1),δ(2),δ(3)) of (1,2,3).
Definition 1.2([8]) Consider complex Banach algebras M and N.Permuting tri-homomorphism is a C-trilinear mappingE:M3→N satisfying
for all Ψ1,Ψ2,Ψ3,Ψ4,Φ1,Φ2,Φ3∈M and for any permutation (δ(1),δ(2),δ(3)) of (1,2,3).
Now, we consider a vector-valued generalized metric space (VVGM-space).
Definition 1.3([9]) Letmbe a positive integer number.We define the partial order set
whereι=(ι1,···,ιm) andγ=(γ1,···,γm) in Xmsatisfy,i=1,···,m, andι →0??ιi →0,i=1,···,m.
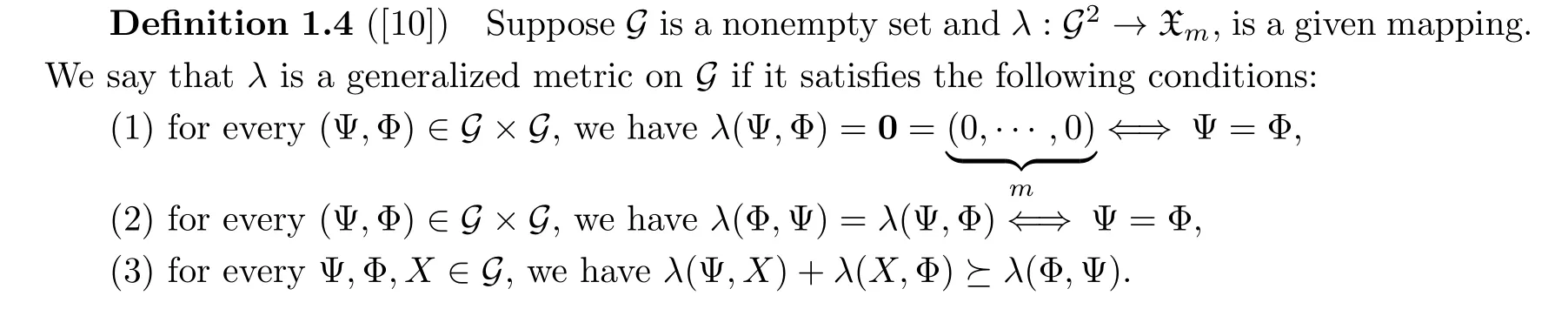
We are ready to present a vector-valued version of the alternative fixed point theorem of Diaz-Margolis [11] in VVGM-space.

This paper will study the complex normed spaceGand the complex Banach spaceQforψ ∈C being fixed with 0/=|ψ|<1.
2 New Control Function by Special Function
In this section, we introduce a series of special functions that we are going to use as a control function.
?Exponential function
Here, we define the complex exponential function as follows:
?Mittag-Leffler function (generalized exponential function)
The special function
is said to be a one-parameter Mittag-Leffler function.
?Hypergeometric function (the Gauss Hypergeometric series)
Now,we define the Hypergeometric function(the Gauss Hypergeometric series).The special function

is called Wright function, in whichm1>-1,p1,Υ∈C.
?Fox-Wright function (the generalized Wright function)
Consider positive vectorsM= (M1,···,Ms),N= (N1,···,Nr), and complex vectorsm= (m1,···,ms), andP= (p1,···,pr).The Fox-Wright function or the generalized Wright function is defined by the series

Note that, (2.1) converges absolutely for|Υ|=Sif?(T)>0.
The functionsHris a extension of the generalized hypergeometric function (which we will present it later).Also,1H1and0H1are the Wright(the Bessel-Maitland)function and Mittag-Leffler function withM1=m1=1, respectively.
?Fox’s H-function (generalized Fox-Wright function)
Now, we present the Fox’s H-function as
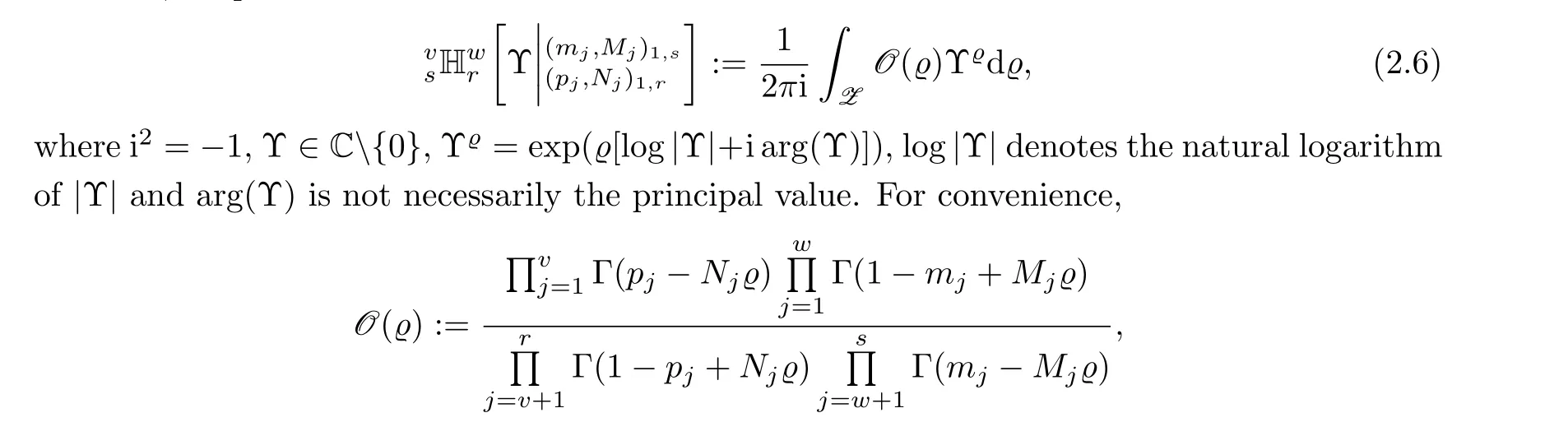
an empty product is interpreted as 1,and the integersv,w,s,rsatisfy the inequalities 0≤w ≤sand 1≤v ≤r.Assume the coefficientsMj >0 (j= 1,···,s) andNj >0 (j= 1,···,r) and the complex parametersmj(j=1,···,s)andpj(j=1,···,r)are so constrained that no poles of integrand in (2.6) coincide, andZis a suitable contour of the Mellin-Barnes type (in the complex?-plane) which separates the poles of one product from those of the other.Further, if we assume

Here, Υ-?= exp(-?[log|Υ|+i arg(Υ)]), Υ/= 0 and i2=-1, and also log|Υ| represents the natural logarithm of|Υ| and arg(Υ) is not necessarily the principle value.
Notice that, an empty product in (2.8), if it occurs, is taken to be one and the poles
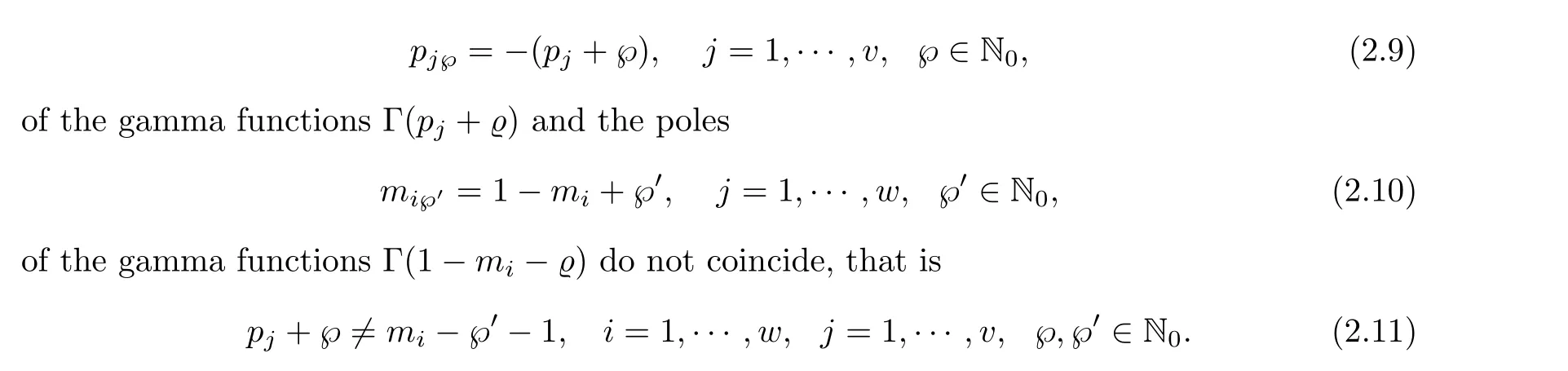
Note that contourZis one of the contours defined before which separates all polespj?in(2.9)to the left and all polesmi?in (2.10) to the right ofZ.
?G-function (generalized Hypergeometric function)
The generalized hypergeometric function is defined by the following generalized hypergeometric series
where Υ∈C,s,r ∈N0, andmi,pj ∈C,i=1,···,sandj=1,···,r.Forz ∈C, we have
Ifmj/=-?,j=1,···,rand?∈N0, then the generalized hypergeometric series (2.12) can be represented in terms of the Mellin-Barnes integral of the form


?Five-parameter Mittag-Leffler function
Letα1,α2,β1,β2,γ ∈Cbe five parameters satisfying Re(α1+α2)>0.The five-parameter Mittag-Leffler function applied to a single variablezis defined by the following power series:

Let a mapping Θ from vector spaceUto normed linear spaceVhas Hyers-Ulam-Rassias stability.If we replace the control function of Hyers-Ulam-Rassias stability with Ξ[Υ], we say Θ has multi-stability property.
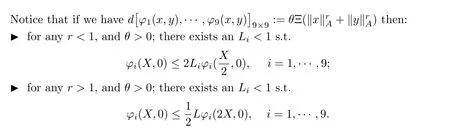
3 Aggregation Function
In this section we introduce the aggregation function to use it as a control function.
Definition 3.1([1]) For fixedn ∈N andI ?R, an aggregation function is a functionA(n):In →Ithat is nondecreasing (in each variable), i.e., for alli ∈[1,···,n]

is an aggregation function.
4 Tri-additive ψ-Functional Inequality (1.1)
In this section, we begin studying the tri-additiveψ-functional inequality (1.1) in complex normed spaces.Some recent developments and related references can be found in [12-15].
Lemma 4.1([6]) Let the mappingL:G3→QsatisfyL(0,Ψ3,Ψ5) =L(Ψ1,0,Ψ5) =L(Ψ1,Ψ3,0)=0 and

which implies that

Hence, we get

where we denote inf?=(inf?,inf?,inf?)=(+∞,+∞,+∞).
We need to show that (ι,λ) is a complete VVGM-space.For the metric part, we prove the triangle inequality:λ(ι,?)(ι,?)+λ(?,?).
Next, we deduce that (ι,λ) is complete.Assume{ωn}is a Cauchy sequence in (ι,λ).Then, for all∈1,∈2,∈3>0 there is an?∈1,∈2,∈3∈N such thatλ(ωm,ωn)(∈1,∈2,∈3) for allm,n ≥?∈1,∈2,∈3.From (4.9), we get



for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈G.According to Lemma 4.1, we conclude that the mappingL′:G3→Qis tri-additive.□
Corollary 4.3Suppose Θ≥0 andr >3 are in R and supposeL:G3→Qis a mapping satisfyingL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 and
for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈G.Then there is a unique tri-additive mappingL′:G3→Qsatisfying
for all Ψ1,Ψ3,Ψ5∈G.
ProofWe define the control functionφby the coefficient
φ(Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6)=Θ(‖Ψ1‖r+‖Ψ2‖r+‖Ψ3‖r+‖Ψ4‖r+‖Ψ5‖r+‖Ψ6‖r), (4.19)for all Ψ1,···,Ψ6∈Gand put P = 21-r.Then the result follows immediately from Theorem 4.2.□
Theorem 4.4Supposeφ:G6→[0,∞) is a function such that

5 Permuting Tri-derivations on Banach Algebras
In this section, we pay attention on permuting tri-derivations on unitalC*-algebras and complex Banach algebras related to the tri-additiveψ-functional inequality (1.1).
Lemma 5.1([16, Lemma 2.1]) SupposeL:G2→Qis a bi-additive mapping such thatL(Λ1Ψ1,Λ2Ψ3) = Λ1Λ2L(Ψ1,Ψ3) for all Ψ1,Ψ3∈Gand Λ1,Λ2∈Δ1:={? ∈C :|?| = 1}.ThenLis C-bilinear.
Lemma 5.2SupposeL:G3→Qis a tri-additive mapping satisfyingL(Λ1Ψ1,Λ2Ψ3,Λ3Ψ5) = Λ1Λ2Λ3L(Ψ1,Ψ3,Ψ5) for all Ψ1,Ψ3,Ψ5∈Ψ5and Λ1,Λ2,Λ3∈Δ1.ThenLis Ctrilinear.
ProofThe proof follows from a similar method to the proof of Theorem [16, Lemma 2.1].□

for all Ψ1,Ψ3,Ψ5∈M, whereφis given in Theorem 4.2.
In addition, if the mappingL:M3→M satisfiesL(Ψ1,Ψ3,Ψ5)=2L(Ψ1,Ψ3,Ψ5) and
for all Ψ1,Ψ2,Ψ3,Φ1,Φ2,Φ3,Ψ5∈M and for every permutation (δ(1),δ(2),δ(3)) of (1,2,3),then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofSuppose Λ1=Λ2=Λ3=1 in(5.2).Then the result follows diectly from Theorem 4.2 and [7, Theorem 3.3].□
Corollary 5.4Suppose Θ≥0 andr >4 are in R, and supposeL: M3→M is a mapping satisfyingL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 and
for all Λ1,Λ2,Λ3∈Δ1and all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there exists a unique Ctrilinear mapping Z:M3→M satisfying
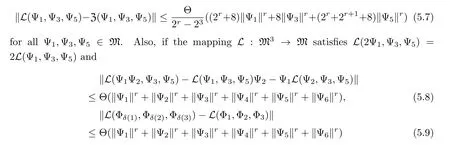
for all Ψ1,Ψ2,Ψ3,Φ1,Φ2,Φ3,Ψ5∈M and for every permutation (δ(1),δ(2),δ(3)) of (1,2,3),then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofPut P = 21-r.It is the coefficient that defines the control functionφby (7.3).Then we apply Theorem 5.3 to complete the proof.□
Theorem 5.5Supposeφ:M6→[0,∞) is a function such that there is 0<P<4 with
for all Ψ1,Ψ3,Ψ5∈M.Also, if the mappingL:M3→M satisfies (5.4), (5.5) andL(2Ψ1,Ψ3,Ψ5) = 2L(Ψ1,Ψ3,Ψ5) for all Ψ1,Ψ3,Ψ5∈M, then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofThe proof follows from a similar method to the proof of Theorem 5.3.□
Corollary 5.6Suppose Θ≥0 andr <3 are in R,and supposeL:M3→M is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then we can find a unique C-trilinear mapping Z:M3→M satisfying
for all Ψ1,Ψ3,Ψ5∈M.Also, if the mappingL:M3→M satisfies (7.6), (7.7) andL(2Ψ1,Ψ3,Ψ5) = 2L(Ψ1,Ψ3,Ψ5) for all Ψ1,Ψ3,Ψ5∈M, then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofPut P = 2r-1.It is the coefficient that defines the control functionφby (7.3).Then we apply Theorem 5.5 to complete the proof.□
Now, let M andU(M) be a unitalC*-algebra with uniteand unitary group, respectively.We have the following theorem:
Theorem 5.7Supposeφ:M6→R is a function satisfying (5.1) and supposeL:M3→M is a mapping satisfying (5.2) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then there exists a unique C-trilinear mapping Z:M3→M satisfying (5.3).
Also, if the mappingL:M3→M satisfies (5.5),L(2β,Ψ3,Ψ5)=2L(β,Ψ3,Ψ5) and
for all Ψ2,Ψ3,Ψ5∈M and allβ ∈U(M), then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofIt follows directly from Theorem 5.3 and [7, Theorem 3.7].□
Remark 5.8By a similar method to the proof last theorem, we can conclude that if(5.13) in Theorem 5.7 is replaced by
for allβ,α,α1,α2∈U(M), then the C-trilinear mapping Z : M3→M is a permuting triderivation.
Corollary 5.9Suppose Θ≥0 andr >3 are in R,and supposeL:M3→M is a mapping satisfying(7.4)andL(Ψ1,0,a)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ3,Ψ5∈M.Then there exists a unique C-trilinear mapping Z : M3→M satisfying (7.5).Furthermore, if the mappingL:M3→M satisfies (7.7),L(2β,Ψ3,Ψ5)=2L(β,Ψ3,Ψ5) and
‖L(βΨ2,Ψ3,Ψ5)-L(β,Ψ3,Ψ5)Ψ2-βL(Ψ2,Ψ3,Ψ5)‖≤Θ(1+‖Ψ2‖r+2‖Ψ3‖r+2‖Ψ5‖r) (5.14)for allβ ∈U(M) and all Ψ2,Ψ3,Ψ5∈M, then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof using Theorem 5.7.□
Theorem 5.10Supposeφ: M6→R is a function satisfying (5.10) and supposeL:M3→M is a mapping satisfying (5.2) andL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ3,Ψ5∈M.Then we can find a unique C-trilinear mapping Z : M3→M satisfying(5.11).In addition, if the mappingL: M3→M satisfies (5.5), (5.13) andL(2β,Ψ3,Ψ5) =2L(β,Ψ3,Ψ5)for all Ψ3,Ψ5∈M and allβ ∈U(M), then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofBy a similar method to the proof of Theorem 5.7, we can get the result.□
Corollary 5.11Suppose Θ≥0 andr <3 are in R, and supposeL:M3→M is a mapping satisfying(7.4)andL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ3,Ψ5∈M.Then there is a unique C-trilinear mapping Z:M3→M satisfying (7.8).
Also, if the mappingL: M3→M satisfies (7.7), (7.9) andL(2β,Ψ3,Ψ5) = 2L(β,Ψ3,Ψ5)for allβ ∈U(M)and all Ψ3,Ψ5∈M,then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof by Theorem 5.10.□
6 Permuting Tri-homomorphisms in Banach Algebras
In this section,we examine several aggregation functions and find the function that has the least error.Then we introduce it as a control function and express the results of the previous section.
Example 6.1We consider the following aggregation function.Let
Table 1 below shows the different values of the aggregations functions for Υ
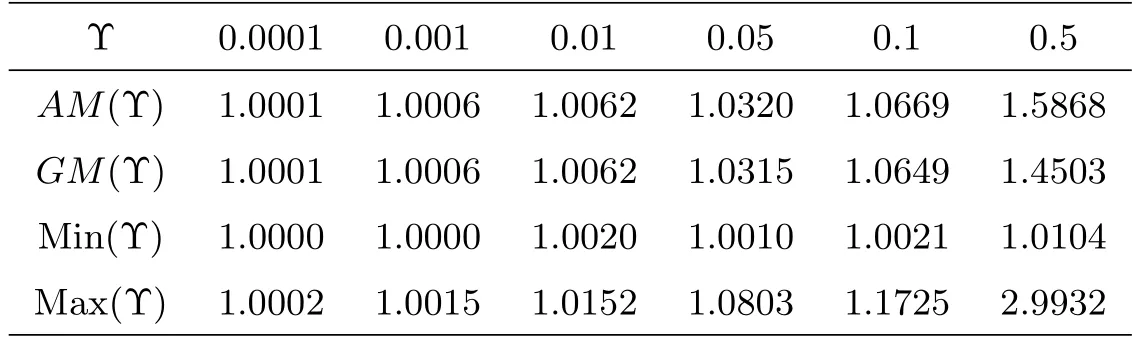
Table 1 The values of the aggregation functions
Figure 1 below shows the different values of the aggregation functions.
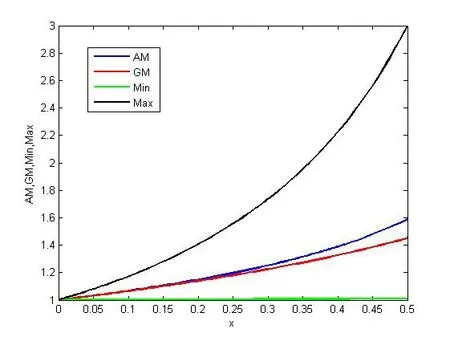
Figure 1
By comparing the values obtained in Table 1 and Figure 1, we conclude that Min is the best control function because it minimizes the error, therefore in the following results, we use the Min as a control function.

for all Ψ1,Ψ3,Ψ5∈M, whereφis given in Theorem 4.2.
Moreover, if the mappingL:M3→N satisfies (5.5) and
‖L(Ψ1Ψ2,Ψ3Ψ4,Ψ5Ψ6)-L(Ψ1,Ψ3,Ψ5)L(Ψ2,Ψ4,Ψ6)‖≤φ(Ψ1,Ψ2,Ψ3,Ψ3,Ψ5,Ψ5), (6.3)for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M, then the C-trilinear mappingE: M3→N is a permuting tri-homomorphism.
ProofIt follows directly from Theorem 5.3 and [7, Theorem 4.1].□
Corollary 6.3Suppose Θ≥0 andr >3 are in R,and supposeL:M3→N is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying
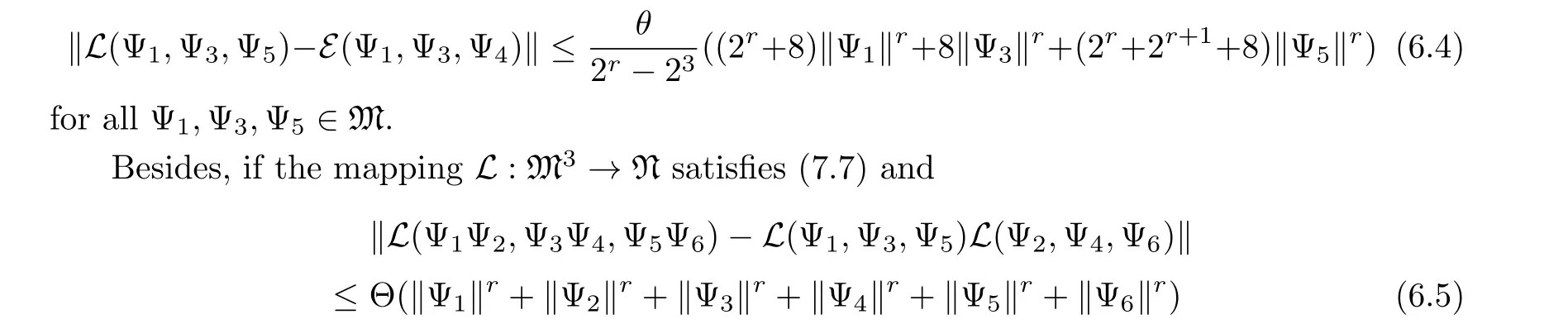
for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M, then the C-trilinear mappingE: M3→N is a permuting tri-homomorphism.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof by Theorem 6.2.□
Theorem 6.4Supposeφ: M6→[0,∞) is a function satisfying (5.10) for 0<P<4,and supposeL: M3→N is a mapping satisfying (5.2) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ3,Ψ4∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying
for all Ψ1,Ψ3,Ψ5∈M.
As well, if the mappingL:M3→N satisfies (5.5) and (6.3), then the C-trilinear mappingE:M3→N is a permuting tri-homomorphism.
ProofBy a similar method to the proof of Theorem 6.2, we can obtain the result.□
Corollary 6.5Suppose Θ≥0 andr <3 are in R,and supposeL:M3→N is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying
for all Ψ1,Ψ3,Ψ5∈M.
Also, if the mappingL: M3→N satisfies (7.7) and (7.11), then the C-trilinear mappingE:M3→N is a permuting tri-homomorphism.
ProofIt is the coefficient tat defines the control functionφby (7.3).Then we complete the proof by Theorem 6.4.□
Assuming M andU(M)are a unitalC*-algebra with uniteand unitary group respectively,we come to the following theorem:
Theorem 6.6Supposeφ:M6→R is a function satisfying (6.1) and supposeL:M3→N is a mapping satisfying (5.2) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying (6.2).
Also, if the mappingL:M3→N satisfies (5.5) and
for allβi,αi ∈U(M),i= 1,2,3, then the C-trilinear mappingE: M3→N is a permuting tri-homomorphism.
ProofUsing Theorem 5.3 and [7, Theorem 4.5], we prove the theorem.□
Corollary 6.7Suppose Θ≥0 andr >6 are in R,and supposeL:M3→N is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there exists a unique C-trilinear mappingE:M3→N satisfying (7.10).
Also, if the mappingL:M3→N satisfies (7.7) and
for allβi,αi ∈U(M),i= 1,2,3, then the C-trilinear mappingE: M3→N is a permuting tri-homomorphism.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof by Theorem 6.6.□
Theorem 6.8Supposeφ: M6→R is a function satisfying (5.10) and supposeL:M3→N is a mapping satisfying (5.2) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying (6.6).
As well, if the mappingL:M3→N satisfies (5.5) and (6.8), then the C-trilinear mappingE:M3→N is a permuting tri-homomorphism.
ProofUsing a similar method to the proof of Theorem 6.6, we can get the result.□
Corollary 6.9Suppose Θ≥0 andr <3 are in R,and supposeL:M3→N is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then we can find a unique C-trilinear mappingE:M3→N satisfying (7.12).
Also, if the mappingL: M3→N satisfies (7.7) and (6.9), then the C-trilinear mappingE:M3→N is a permuting tri-homomorphism.
Proof It is the coefficient that defines the control functionφby (7.3).The we complete the proof by Theorem 6.8.□
7 Applications
Consider the following aggregation function by valued multi control function

for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈G.Then there is a unique tri-additive mappingL′:G3→Qsatisfying
for all Ψ1,Ψ3,Ψ5∈G.
ProofWe define the control functionφby the coefficient
for all Ψ1,···,Ψ6∈Gand put P = 21-r.Then the result follows immediately from Theorem 4.2.□
Corollary 7.2Assume that Θ≥0 andr <3 are in R, and supposeL:G3→Qis a mapping satisfyingL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 and(7.1).Then we can find a unique tri-additive mappingL′:G3→Qsatisfying
for all Ψ1,Ψ3,Ψ5∈G.
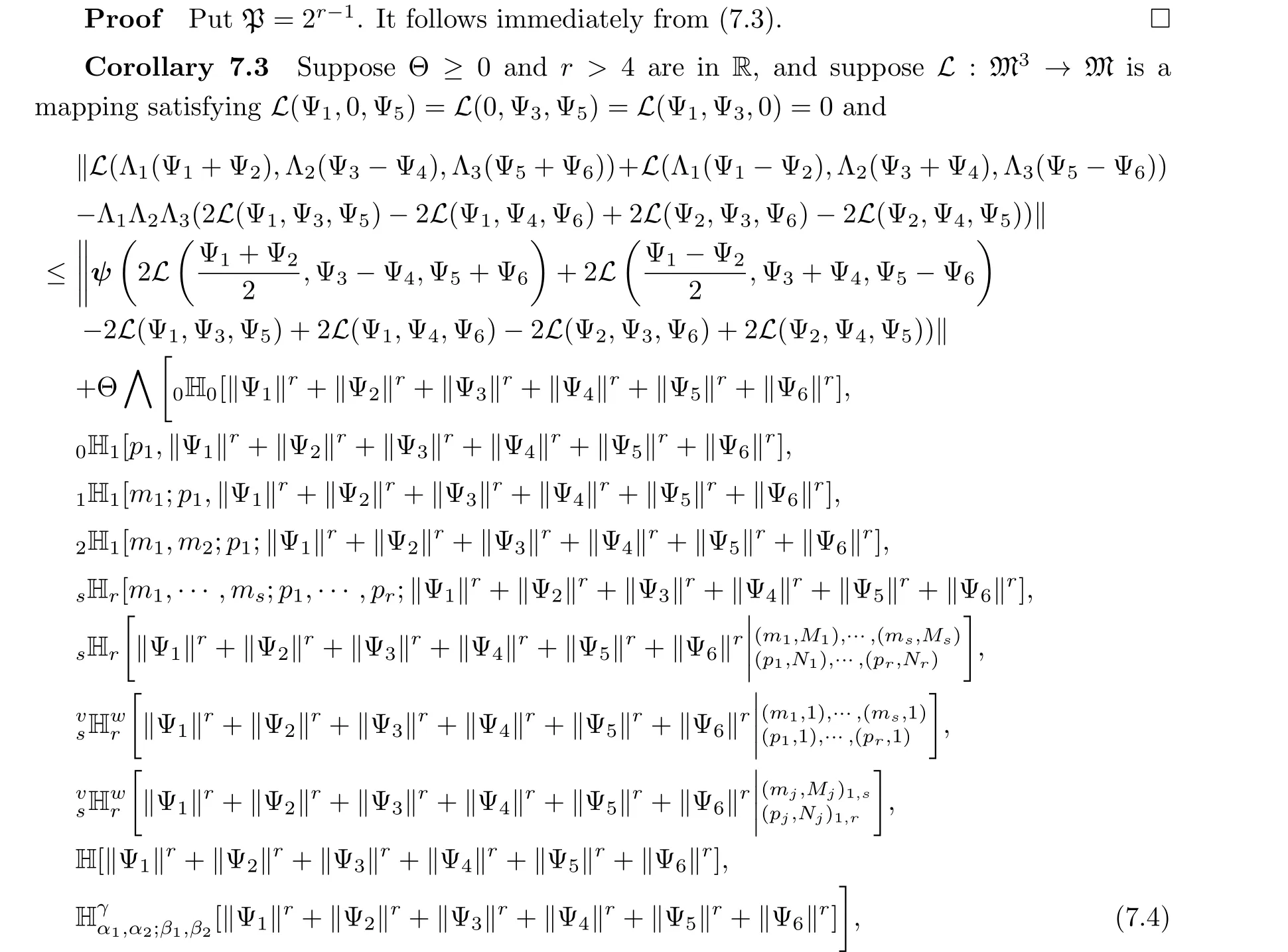
for all Λ1,Λ2,Λ3∈Δ1and all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there exists a unique Ctrilinear mapping Z:M3→M satisfying
for all Ψ1,Ψ3,Ψ5∈M.Also, if the mappingL: M3→M satisfiesL(2Ψ1,Ψ3,Ψ5) =2L(Ψ1,Ψ3,Ψ5) and
for all Ψ1,Ψ2,Ψ3,Φ1,Φ2,Φ3,Ψ5∈M and for every permutation (δ(1),δ(2),δ(3)) of (1,2,3),then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofPut P = 21-r.It is the coefficient that defines the control functionφby (7.3).Then we apply Theorem 5.3 to complete the proof.□
Corollary 7.4Suppose Θ≥0 andr <3 are in R,and supposeL:M3→M is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then we can find a unique C-trilinear mapping Z:M3→M satisfying
for all Ψ1,Ψ3,Ψ5∈M.Also, if the mappingL:M3→M satisfies (7.6), (7.7) andL(2Ψ1,Ψ3,Ψ5) = 2L(Ψ1,Ψ3,Ψ5) for all Ψ1,Ψ3,Ψ5∈M, then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofPut P = 2r-1.It is the coefficient that defines the control functionφby (7.3).Then we apply Theorem 5.5 to complete the proof.□
Corollary 7.5Suppose Θ≥0 andr >3 are in R,and supposeL:M3→M is a mapping satisfying(7.4)andL(Ψ1,0,a)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ3,Ψ5∈M.Then there exists a unique C-trilinear mapping Z : M3→M satisfying (7.5).Furthermore, if the mappingL:M3→M satisfies (7.7),L(2β,Ψ3,Ψ5)=2L(β,Ψ3,Ψ5) and
for allβ ∈U(M) and all Ψ2,Ψ3,Ψ5∈M, then the C-trilinear mapping Z : M3→M is a permuting tri-derivation.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof using Theorem 5.7.□
Corollary 7.6Suppose Θ≥0 andr <3 are in R,and supposeL:M3→M is a mapping satisfying (7.4) andL(Ψ1,0,Ψ5) =L(0,Ψ3,Ψ5) =L(Ψ1,Ψ3,0) = 0 for all Ψ1,Ψ3,Ψ5∈M.Then there is a unique C-trilinear mapping Z:M3→M satisfying (7.8).
Also, if the mappingL: M3→M satisfies (7.7), (7.9) andL(2β,Ψ3,Ψ5) = 2L(β,Ψ3,Ψ5)for allβ ∈U(M)and all Ψ3,Ψ5∈M,then the C-trilinear mapping Z:M3→M is a permuting tri-derivation.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof by Theorem 5.10.□
Corollary 7.7Suppose Θ≥0 andr >3 are in R,and supposeL:M3→N is a mapping satisfying(7.4)andL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying
for all Ψ1,Ψ3,Ψ5∈M.
Besides, if the mappingL:M3→N satisfies (7.7) and
for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M, then the C-trilinear mappingE: M3→N is a permuting tri-homomorphism.
ProofIt is the coefficient that defines the control functionφby(7.3).Then we complete the proof by Theorem 6.2.□
Corollary 7.8Suppose Θ≥0 andr <3 are in R,and supposeL:M3→N is a mapping satisfying(7.4)andL(Ψ1,0,Ψ5)=L(0,Ψ3,Ψ5)=L(Ψ1,Ψ3,0)=0 for all Ψ1,Ψ2,Ψ3,Ψ4,Ψ5,Ψ6∈M.Then there is a unique C-trilinear mappingE:M3→N satisfying
for all Ψ1,Ψ3,Ψ5∈M.
Also, if the mappingL: M3→N satisfies (7.7) and (7.11), then the C-trilinear mappingE:M3→N is a permuting tri-homomorphism.
ProofIt is the coefficient tat defines the control functionφby (7.3).Then we complete the proof by Theorem 6.4.□
8 Conclusion
Applying the CRM derived from an alternative fixed point theorem, we stabilized a triadditiveψ-functional inequality forψbeing a fixed complex number with 0/=|ψ|<1.In addition, we studied permuting tri-homomorphisms and permuting tri-derivations in unitalC*-algebras and Banach algebras associated with the above inequality.
Conflict of InterestThe authors declare no conflict of interest.
Authors’ contributionsThe authors equally conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
 Acta Mathematica Scientia(English Series)2024年1期
Acta Mathematica Scientia(English Series)2024年1期
- Acta Mathematica Scientia(English Series)的其它文章
- THE RIEMANN PROBLEM FOR ISENTROPIC COMPRESSIBLE EULER EQUATIONS WITH DISCONTINUOUS FLUX*
- THE BOUNDEDNESS OF OPERATORS ON WEIGHTED MULTI-PARAMETER LOCAL HARDY SPACES*
- INTERFACE BEHAVIOR AND DECAY RATES OF COMPRESSIBLE NAVIER-STOKES SYSTEM WITH DENSITY-DEPENDENT VISCOSITY AND A VACUUM*
- CONVEXITY OF THE FREE BOUNDARY FOR AN AXISYMMETRIC INCOMPRESSIBLE IMPINGING JET*
- SOME PROPERTIES OF THE INTEGRATION OPERATORS ON THE SPACES F(p,q,s)*
- COMPLETE K¨AHLER METRICS WITH POSITIVE HOLOMORPHIC SECTIONAL CURVATURES ON CERTAIN LINE BUNDLES (RELATED TO A COHOMOGENEITY ONE POINT OF VIEW ON A YAU CONJECTURE)*
