求數(shù)列通項(xiàng)公式的十種常見題型

田素偉

(上海市泥城中學(xué),上海 201300)

數(shù)列是高考的必考內(nèi)容,而數(shù)列的通項(xiàng)公式是數(shù)列的核心.如果題目中沒有直接給出數(shù)列是等差數(shù)列或等比數(shù)列,如何把題目中的條件通過變形轉(zhuǎn)化為等差數(shù)列或等比數(shù)列,進(jìn)而正確地求出數(shù)列的通項(xiàng)公式?下面介紹幾種常見的數(shù)列通項(xiàng)公式的求法.

1 直接利用等差(等比)數(shù)列的通項(xiàng)公式

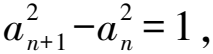
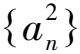
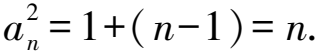
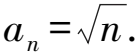
兩邊同時(shí)開平方,得

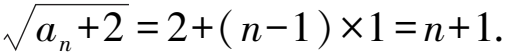
所以an=n2+2n-1.

2 用待定系數(shù)法求數(shù)列的通項(xiàng)公式

例2 數(shù)列{an}滿足an=2an-1+3(n≥2)且a1=1,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析由an=2an-1+3(n≥2),可設(shè)

an+x=2(an-1+x)(n≥2),

則an=2an-1+x(n≥2).

比較系數(shù)可得x=3.

所以an+3=2(an-1+3)(n≥2).

故{an+3}是以4為首項(xiàng),2為公比的等比數(shù)列.

所以an+3=4×2n-1=2n+1．

所以an=2n+1-3.

點(diǎn)評(píng)形如an+1=Aan+B(A≠1且B≠0)或an+1=Aan+Bn(A≠1且B≠0),A,B均為常數(shù)的等式,常用待定系數(shù)法轉(zhuǎn)化為等比數(shù)列再求通項(xiàng)公式.

變式已知數(shù)列{an}滿足an+1=2an+3n且a1=1,n∈N*,求數(shù)列{an}的通項(xiàng)公式[1].

比較系數(shù)可得x=-1.

所以an=3n-2n.

3 構(gòu)造特征函數(shù)

例3數(shù)列{an}滿足an=4an-1+3(n∈N*,n≥2)且a1=0,求數(shù)列{an}的通項(xiàng)公式.

解析設(shè)f(x)=4x+3,令x=4x+3,解得x=-1.

由an=4an-1+3(n≥2),

an-(-1)=4an-1+3-(-1).

所以an+1=4(an-1+1).

所以{an+1}是以1為首項(xiàng),4為公比的等比數(shù)列.

所以an+1=4n-1．

所以數(shù)列{an}的通項(xiàng)公式為an=4n-1-1.

變式數(shù)列{an}中,an是1和anan+1的等差中項(xiàng),a1=2,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析因?yàn)閍n是1和anan+1的等差中項(xiàng),

所以2an=1+anan+1.

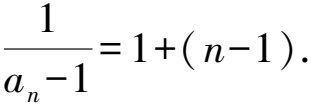
4 對(duì)于周期數(shù)列先求其周期

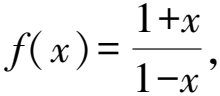
所以anan+2=-1.

所以an+4an+2=-1.

所以an+4=an.

所以數(shù)列{an}的周期為4.

因?yàn)閍1=2,

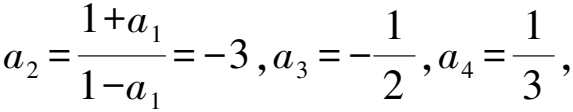
5 遞推關(guān)系式兩邊取對(duì)數(shù)

已知的遞推關(guān)系式含冪指數(shù)或乘積的形式時(shí),利用取對(duì)數(shù)方法進(jìn)行變形轉(zhuǎn)化為等差數(shù)列或等比數(shù)列,再求其通項(xiàng)公式.

例5 已知數(shù)列{an}滿足a1=1,an+1=2nan,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析因?yàn)閍n+1=2nan,a1=1,所以an>0.

兩邊同時(shí)取以2為底的對(duì)數(shù),得

log2an+1=log22nan.

所以log2an+1=log2an+n.

設(shè)bn=log2an,則bn+1=log2an+1.

所以bn+1=bn+n.

所以bn+1-bn=n.

所以b2-b1=1,

b3-b2=2,

b4-b3=3,

…………

bn-bn-1=n-1.

以上各等式兩邊分別相加可得

又因?yàn)閎n=log2an,

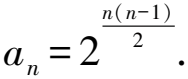
點(diǎn)評(píng)注意利用取對(duì)數(shù)的方法要滿足an>0這一條件.另外本題還可以利用累乘法求解.

6 形如an=f(n)an-1+g(n)(n∈N*,n≥2)的數(shù)列

6.1 利用累加法

當(dāng)f(n)=1時(shí),形如an=an-1+g(n)(n≥2),n∈N*的形式,可利用累加法求數(shù)列的通項(xiàng)公式[2].

例6已知數(shù)列{an}滿足a1=2,且an+1-an=2n+1,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析因?yàn)閍n+1-an=2n+1,所以

以上各式兩邊分別相加

an-a1=2(1+2+3+4+…+n-1)+1×(n-1).

所以an=n2.

6.2 利用累乘法或者等式兩邊同時(shí)取對(duì)數(shù)的方法

當(dāng)g(n)=0時(shí),形如an=f(n)an-1(n≥2)的形式利用累乘法或者等式兩邊同時(shí)取對(duì)數(shù)的方法求數(shù)列的通項(xiàng)公式(見例10).

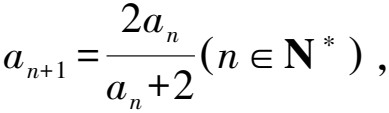
8 與正整數(shù)有關(guān)的和的等式求通項(xiàng)公式用分離法

例8 已知數(shù)列{an}的前n項(xiàng)和為Sn,且S1+2S2+3S3+…+nSn=n3,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析由已知,n≥2時(shí),

S1+2S2+3S3+…+(n-1)Sn-1+nSn=n3,

①

S1+2S2+3S3+…+(n-1)Sn-1=(n-1)3,

②

由①-②,得

nSn=n3-(n-1)3.

又當(dāng)n=1時(shí),S1=1也符合上式,

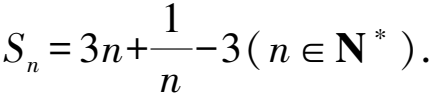
當(dāng)n=1時(shí),a1=1,

9 關(guān)于數(shù)列的奇數(shù)項(xiàng)和偶數(shù)項(xiàng)的通項(xiàng)公式

例9已知數(shù)列{an}滿足a1=1,a2=2,an+2-an=(-1)n+2,n∈N*,求數(shù)列{an}的通項(xiàng)公式.

解析由已知條件an+2-an=(-1)n+2可知:當(dāng)n為奇數(shù)時(shí),an+2-an=1,{a2n-1}是以1為首項(xiàng),1為公差的等差數(shù)列;

當(dāng)n為偶數(shù)時(shí),an+2-an=3,{a2n}是以2為首項(xiàng),3為公差的等差數(shù)列.

所以當(dāng)n=2k-1(k∈N*)時(shí),

a2k-1=a1+(k-1)d=1+(k-1)×1=k.

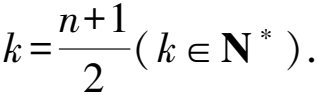
當(dāng)n=2k(k∈N*)時(shí),

a2k=a2+(k-1)d=2+(k-1)3=3k-1.

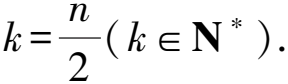
所以所求數(shù)列的通項(xiàng)公式是

點(diǎn)評(píng)根據(jù)遞推公式得出奇數(shù)項(xiàng)數(shù)列和偶數(shù)項(xiàng)數(shù)列各為等差數(shù)列,再結(jié)合已知數(shù)列的通項(xiàng)公式來求解問題,這里要注意奇數(shù)項(xiàng)和偶數(shù)項(xiàng)的首項(xiàng).注意等式或不等式中出現(xiàn)(-1)n,一般都要分n為奇數(shù)和偶數(shù)進(jìn)行討論.

10 形如或a1=Aan+1-an=f(n)(A為常數(shù),n∈N*)的數(shù)列求通項(xiàng)公式用累乘法或累加法

例10設(shè)數(shù)列{an}的前n項(xiàng)和為Sn,且a1=1,{Sn+nan}為常數(shù)列,求數(shù)列{an}的通項(xiàng)公式.

分析由已知可得出Sn+nan=2,進(jìn)而可知Sn-1+(n-1)an-1=2(n≥2),兩式兩邊分別相減得(n+1)an=(n-1)an-1,然后利用累乘法求出an即可.

解析因?yàn)閧Sn+nan}為常數(shù)列且a1=1,

所以Sn+nan=S1+1×a1=2,

(1)當(dāng)n=1時(shí),因?yàn)镾1+1·a1=2,所以a1=1.

(2)當(dāng)n≥2時(shí),由已知Sn+nan=2,

③

所以Sn-1+(n-1)an-1=2,

④

③-④,得(n+1)an=(n-1)an-1.

…………

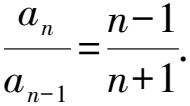
以上等式兩邊分別相乘,得

點(diǎn)評(píng)本題考查利用an與Sn的關(guān)系求數(shù)列的通項(xiàng),考查累乘法求通項(xiàng),合理遞推作差是解答的關(guān)鍵.本題注意要寫出前四個(gè)等式和最后兩個(gè)等式,可以方便觀察,本題著重考查推理與運(yùn)算能力．