全局3-彩虹控制數(shù)與3-彩虹控制數(shù)之差為2和3的樹的刻畫

郝 國 亮, 曾 淑 婷, 莊 蔚, 謝 智 紅

(1.東華理工大學 理學院,江西 南昌 330013;2.菏澤學院 數(shù)學與統(tǒng)計學院,山東 菏澤 274015;3.廈門理工學院 數(shù)學與統(tǒng)計學院,福建 廈門 361024;4.菏澤學院 商學院,山東 菏澤 274015 )

0 引 言

圖的控制理論是圖論中一個重要的研究領域,基于不同的研究背景,圖的經典控制數(shù)衍生出了許多不同類型的控制參數(shù)[1-3],其中圖的彩虹控制數(shù)的概念最早出現(xiàn)于2008年[4].隨后,研究者們陸續(xù)給出了彩虹控制數(shù)的許多研究成果[5-8].Alqesmah等[9]和Amjadi等[10]分別引入了彩虹控制數(shù)的一個衍生變量,即圖的全局彩虹控制數(shù).Amjadi等[10]刻畫了全局2-彩虹控制數(shù)與2-彩虹控制數(shù)之差為1和2的樹.受此結果的啟發(fā),本文主要刻畫全局3-彩虹控制數(shù)與3-彩虹控制數(shù)之差為2和3的所有樹.

1 基本概念

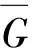
稱無圈的連通圖為樹.在樹中,度為1的頂點稱為葉子點,只與1個葉子點相鄰的頂點稱為弱支撐點,至少與2個葉子點相鄰的頂點稱為強支撐點,弱支撐點和強支撐點統(tǒng)稱為支撐點.雙星圖Sp,q是指恰好有2個支撐點的樹且它們分別與p和q個葉子點相鄰.稱n≥3階完全二部圖K1,n-1為星形圖,且稱度為n-1的頂點為其中心.病態(tài)蜘蛛樹是指對星形圖K1,n-1(n≥3)至多剖分n-2條邊所得到的圖,稱星形圖的中心為病態(tài)蜘蛛樹的頭,稱與頭距離為1和2的葉子點分別為病態(tài)腳和健康腳.用Π表示有2個健康腳且至少有3個病態(tài)腳的病態(tài)蜘蛛樹構成的集合.

2 主要結論

為得到本文的主要結果,首先給出下列引理.

引理1設u是樹T中至少與3個葉子點相鄰的強支撐點,則一定存在一個γr3(T)-函數(shù)f使得f(u)={1,2,3}且對任意與u相鄰的葉子點x,f(x)=?.

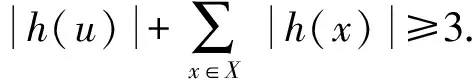
γr3(T)≤ω(f)=

ω(h)+3-3=

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味著f也是一個γr3(T)-函數(shù).故f就是所求的γr3(T)-函數(shù).

引理2設P=u1u2u3u4u5是樹T中的一條路使得d(u1)=d(u5)=1且d(u2)=d(u4)=2,則一定存在一個γr3(T)-函數(shù)f使得f(u1)=f(u5)={1},f(u2)=f(u4)=?且{2,3}?f(u3).

證明設h是一個γr3(T)-函數(shù).因為d(u1)=d(u5)=1,所以|h(u1)|+|h(u2)|≥1且|h(u4)|+|h(u5)|≥1.如果|h(u1)|+|h(u2)|=1或|h(u4)|+|h(u5)|=1,則不妨設|h(u1)|+|h(u2)|=1.于是由γr3(T)-函數(shù)的定義知,|h(u1)|=1且h(u2)=?.因此不妨設h(u1)={1}.又因為N(u2)={u1,u3},所以h(u1)∪h(u3)={1,2,3},于是{2,3}?h(u3).注意到d(u4)=2且d(u5)=1,因此由γr3(T)-函數(shù)的定義知:如果h(u3)={2,3},則h(u4)=?且h(u5)={1};如果h(u3)={1,2,3},則h(u4)=?且|h(u5)|=1.于是不妨設h(u5)={1}.故在這種情況下,f=h就是所求的γr3(T)-函數(shù).

如果|h(u1)|+|h(u2)|≥2且|h(u4)|+|h(u5)|≥2,則定義樹T的一個3-彩虹控制函數(shù)f:V(T)→2{1,2,3}使得f(u1)=f(u5)={1},f(u2)=f(u4)=?,f(u3)=h(u3)∪{2,3}且當x?{u1,u2,…,u5}時,f(x)=h(x).于是

γr3(T)≤ω(f)=

ω(h)+(|f(u1)|+|f(u2)|+

|f(u4)|+|f(u5)|)-(|h(u1)|+

|h(u2)|+|h(u4)|+|h(u5)|)+

(|f(u3)|-|h(u3)|)≤

ω(h)+2-4+(|h(u3)∪{2,3}|-

|h(u3)|)≤

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味著f也是一個γr3(T)-函數(shù).故f就是所求的γr3(T)-函數(shù).

引理3設u1是樹T中與葉子點u2和強支撐點u3都相鄰的2度弱支撐點,則一定存在一個γr3(T)-函數(shù)f使得f(u1)=?,f(u2)={1},f(u3)={1,2,3}且對任意與u3相鄰的葉子點x,f(x)=?.

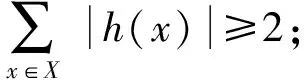
γr3(T)≤ω(f)=

ω(h)+4-4=

ω(h)=

γr3(T)

因此ω(f)=γr3(T).意味著f也是一個γr3(T)-函數(shù).故f就是所求的γr3(T)-函數(shù).

引理4如果T=S1,t(t≥3)或T∈Π,則γgr3(T)-γr3(T)=2.

證明首先假設T=S1,t(t≥3).設v1和v2是雙星圖S1,t的支撐點且設N(v2){v1}={v3}.不難驗證,函數(shù)f使得f(v1)={1,2,3},f(v3)={1}且當x?{v1,v3}時,f(x)=?是一個γr3(T)-函數(shù),并且函數(shù)h使得h(v1)=h(v2)={1,2,3}且當x?{v1,v2}時,h(x)=?是一個γgr3(T)-函數(shù).因此γgr3(T)-γr3(T)=2.

其次假設T∈Π.設v0是病態(tài)蜘蛛樹T∈Π的頭.令v1和v2是樹T的健康腳且對于任意i∈{1,2},令ui是與v0和vi都相鄰的弱支撐點.不難驗證,函數(shù)f使得f(v0)={1,2,3},f(v1)=f(v2)={1}且當x?{v0,v1,v2}時,f(x)=?是一個γr3(T)-函數(shù),并且函數(shù)h使得h(v0)=h(u1)={1,2,3},h(v2)={1}且當x?{v0,u1,v2}時,h(x)=?是一個γgr3(T)-函數(shù).因此γgr3(T)-γr3(T)=2.

命題1設P=v1v2…vk是樹T的一條最長路且k≥4.若d(v2)≥3或d(vk-1)≥3,則γgr3(T)-γr3(T)≤2且等式成立當且僅當T=S1,t(t≥3).

證明首先給出以下斷言.

斷言1如果d(v2)=3或d(vk-1)=3,則γgr3(T)-γr3(T)≤1.

斷言1的證明不失一般性,假設d(v2)=3且設N(v2){v1,v3}={u}.令f是一個γr3(T)-函數(shù).注意到v2是度為3的強支撐點,顯然有|f(v1)|+|f(v2)|+|f(u)|≥2.

若|f(v1)|+|f(v2)|+|f(u)|=2,則由γr3(T)-函數(shù)的定義知,f(v2)=?,|f(v1)|=|f(u)|=1且f(v1)∪f(v3)∪f(u)={1,2,3}.于是不妨設f(v1)={1},f(u)={2}且3∈f(v3).故不難看出函數(shù)h:V(T)→2{1,2,3}使得h(v2)={3}且當x∈V(T){v2}時,h(x)=f(x)是樹T的全局3-彩虹控制函數(shù).因此

γgr3(T)≤ω(h)=

ω(f)+|h(v2)|-|f(v2)|=

ω(f)+1=γr3(T)+1

若|f(v1)|+|f(v2)|+|f(u)|≥3,則定義樹T的一個全局3-彩虹控制函數(shù)h:V(T)→2{1,2,3}使得h(v1)={1},h(u)={2},h(v2)={3},h(v3)=f(v3)∪{3}且當x∈V(T){v1,v2,v3,u}時,h(x)=f(x).于是

γgr3(T)≤ω(h)=

ω(f)+(|h(u)|+|h(v1)|+

|h(v2)|)-(|f(u)|+|f(v1)|+

|f(v2)|)+(|h(v3)|-|f(v3)|)≤

ω(f)+3-3+(|f(v3)∪{3}|-

|f(v3)|)≤

ω(f)+1=

γr3(T)+1

斷言1得證.

斷言2如果k=4且d(v2)和d(vk-1)中至少有一個不小于4,則γgr3(T)-γr3(T)≤2且等式成立當且僅當T=S1,t(t≥3).

斷言2的證明不失一般性,假設d(v2)≥4.因為k=4,所以樹T是雙星圖.如果d(v3)=2,則T=S1,t,其中t=d(v2)-1≥3,于是由引理4知,γgr3(T)-γr3(T)=2.如果d(v3)=3,則由斷言1知,γgr3(T)-γr3(T)≤1.如果d(v3)≥4,則函數(shù)f:V(T)→2{1,2,3}使得f(v2)=f(v3)={1,2,3}且當x?{v2,v3}時,f(x)=?既是一個γr3(T)-函數(shù)又是一個γgr3(T)-函數(shù),因此γgr3(T)=γr3(T).斷言2得證.

斷言3如果k≥5且d(v2)和d(vk-1)中至少有一個不小于4,則γgr3(T)-γr3(T)≤1.

斷言3的證明不失一般性,假設d(v2)≥4.注意到v2是至少與3個葉子點相鄰的強支撐點,則由引理1,不妨設f是一個γr3(T)-函數(shù)使得f(v2)={1,2,3}且對任意x∈N(v2){v3},f(x)=?.

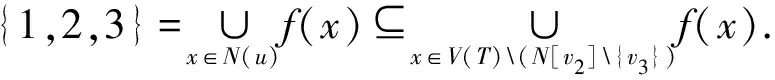
γgr3(T)≤ω(h)=

ω(f)+|h(v3)|-|f(v3)|=

ω(f)+|f(v3)∪{1}|-|f(v3)|≤

ω(f)+1=

γr3(T)+1

如果對任意u?N[v2],都有f(u)≠?成立,則函數(shù)h:V(T)→2{1,2,3}使得h(v3)=f(v3)∪{1},h(v4)={2},h(v5)={3}且當x∈V(T){v3,v4,v5}時,h(x)=f(x)是樹T的全局3-彩虹控制函數(shù),因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v4)|+|h(v5)|)-

(|f(v4)|+|f(v5)|)+

(|h(v3)|-|f(v3)|)≤

ω(f)+2-2+(|f(v3)∪{1}|-

|f(v3)|)≤

ω(f)+1=

γr3(T)+1

斷言3得證.

由斷言1、2和3知,命題1成立.

命題2設P=v1v2…vk是樹T的一條最長路且k≥4.若d(v2)=d(vk-1)=2,則γgr3(T)-γr3(T)≤2且等式成立當且僅當T∈Π.

證明如果k=4,則因為d(v2)=d(v3)=2,所以T=v1v2v3v4是含有4個頂點的路,因此γgr3(T)=4=γr3(T).下面設k≥5.首先給出以下斷言.

斷言1如果N(v3){v2,v4}=?,則γgr3(T)-γr3(T)≤1.

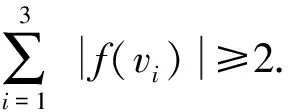
γgr3(T)≤ω(h)=

ω(f)+3-2=

ω(f)+1=

γr3(T)+1

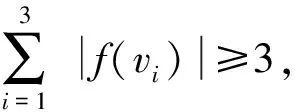
γgr3(T)≤ω(h)=

(|h(v4)|-|f(v4)|)≤

ω(f)+3-3+(|f(v4)∪{3}|-

|f(v4)|)≤

ω(f)+1=

γr3(T)+1

斷言1得證.

斷言2如果N(v3){v2,v4}中存在一個度至少為2的頂點,則γgr3(T)-γr3(T)≤1.

斷言2的證明注意到k≥5.因為P=v1v2…vk是樹T的一條最長路且N(v3){v2,v4}中存在一個度至少為2的頂點,所以N(v3){v2,v4}中一定含有樹T的強支撐點或弱支撐點.如果N(v3){v2,v4}中存在一個強支撐點,則因為k≥5,所以類似于命題1中斷言1和3的證明可得,γgr3(T)-γr3(T)≤1.下面假設N(v3){v2,v4}中存在一個弱支撐點,不妨設為u1.令N(u1){v3}={u2}.由于d(v1)=d(u2)=1且d(v2)=d(u1)=2,則由引理2,不妨設f是一個γr3(T)-函數(shù)使得f(v1)=f(u2)={1},f(v2)=f(u1)=?且{2,3}?f(v3).

如果k=5,則因為d(v4)=2,d(v5)=1且{2,3}?f(v3),所以由γr3(T)-函數(shù)的定義知,f(v4)=?且|f(v5)|=1,不妨設f(v5)={1};如果k≥6且f(vk-1)和f(vk)都不為?,則因為d(vk)=1,所以由γr3(T)-函數(shù)的定義知,|f(vk)|=1,不妨設f(vk)={1}.于是這兩種情況下,不難看出函數(shù)h:V(T)→2{1,2,3}使得h(v1)={2},h(v2)={3}且當x?{v1,v2}時,h(x)=f(x)是樹T的全局3-彩虹控制函數(shù).因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v1)|+|h(v2)|)-

(|f(v1)|+|f(v2)|)=

ω(f)+2-1=

γr3(T)+1

下面考慮最后一種情況,即k≥6且f(vk-1)和f(vk)中至少有一個為?.注意到由γr3(T)-函數(shù)的定義知,若f(vk-1)=?,則f(vk-2)∪f(vk)={1,2,3};若f(vk)=?,則f(vk-1)={1,2,3}.于是不難驗證函數(shù)h:V(T)→2{1,2,3}使得h(v4)=f(v4)∪{1}且當x∈V(T){v4}時,h(x)=f(x)是樹T的全局3-彩虹控制函數(shù).因此

γgr3(T)≤ω(h)=

ω(f)+|h(v4)|-|f(v4)|=

ω(f)+|f(v4)∪{1}|-|f(v4)|≤

ω(f)+1=

γr3(T)+1

斷言2得證.

斷言3如果|N(v3){v2,v4}|=1且N(v3){v2,v4}中的頂點為葉子點,則γgr3(T)-γr3(T)≤1.

斷言3的證明設N(v3){v2,v4}={u}且設f是一個γr3(T)-函數(shù).由于d(v1)=d(u)=1,則顯然有

|f(v1)|+|f(v2)|≥1且|f(v3)|+|f(u)|≥1

(1)

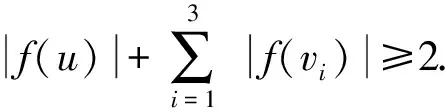
γgr3(T)≤ω(h)=

ω(f)+4-3=

γr3(T)+1

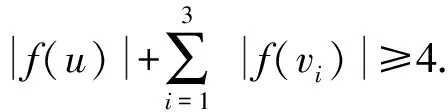
γgr3(T)≤ω(h)=

(|h(v4)|-|f(v4)|)≤

ω(f)+4-4+(|f(v4)∪{3}|-

|f(v4)|)≤

ω(f)+1=

γr3(T)+1

斷言3得證.

斷言4如果|N(v3){v2,v4}|≥2且N(v3){v2,v4}中的頂點都為葉子點,則γgr3(T)-γr3(T)≤2且等式成立當且僅當T∈Π.

斷言4的證明注意到k≥5.首先假設k=5.若|N(v3){v2,v4}|=2,則不妨設N(v3){v2,v4}={u1,u2}.又因為d(v2)=d(v4)=2,所以V(T)={v1,v2,v3,v4,v5,u1,u2}.于是函數(shù)f使得f(v1)=f(v5)={1},f(v3)={1,2,3}且當x?{v1,v3,v5}時,f(x)=?是一個γr3(T)-函數(shù),并且函數(shù)h使得h(v1)=h(v5)={1},h(v2)=h(v4)=?,h(v3)={2,3},h(u1)={2}且h(u2)={3}是一個γgr3(T)-函數(shù).因此γgr3(T)-γr3(T)=6-5=1.若|N(v3){v2,v4}|≥3,則T∈Π,于是由引理4知,γgr3(T)-γr3(T)=2.

其次假設k≥6.如果N(vk-2){vk-3,vk-1}=?,則類似于斷言1的證明可得γgr3(T)-γr3(T)≤1.如果N(vk-2){vk-3,vk-1}中存在度至少為2的頂點,則類似于斷言2的證明可得γgr3(T)-γr3(T)≤1.如果|N(vk-2){vk-3,vk-1}|=1且N(vk-2){vk-3,vk-1}中的頂點為葉子點,則類似于斷言3的證明可得γgr3(T)-γr3(T)≤1.下設|N(vk-2){vk-3,vk-1}|≥2且N(vk-2){vk-3,vk-1}中的頂點都為葉子點.

由于N(v2)={v1,v3}且v1和v3分別是葉子點和強支撐點,則由引理3,不妨設f是一個γr3(T)-函數(shù)使得f(v1)={1},f(v2)=?,f(v3)={1,2,3}且對任意x∈N(v3){v2,v4},f(x)=?.由于d(vk-1)=2,d(vk)=1且vk-2是強支撐點,則再次由引理3,不妨設f(vk)={1},f(vk-1)=?,f(vk-2)={1,2,3}且對任意x∈N(vk-2){vk-3,vk-1},f(x)=?.于是不難看出函數(shù)h:V(T)→2{1,2,3}使得h(v1)={2},h(v2)={3}且當x?{v1,v2}時,h(x)=f(x)是樹T的全局3-彩虹控制函數(shù),因此

γgr3(T)≤ω(h)=

ω(f)+(|h(v1)|+|h(v2)|)-

(|f(v1)|+|f(v2)|)=

ω(f)+2-1=

γr3(T)+1

斷言4得證.

由斷言1～4可知,命題2成立.

定理1對任意樹T,下列結論成立:

(1)γgr3(T)-γr3(T)=2當且僅當T∈{K1,4,S1,t(t≥3)}∪Π.

(2)γgr3(T)-γr3(T)=3當且僅當T=K1,n-1(n≥6).

證明設樹T含有n個頂點.如果n≤3,則易見γgr3(T)=n=γr3(T).下面設n≥4.如果樹T的直徑為2,即T=K1,n-1,則當n=4時,γgr3(T)-γr3(T)=4-3=1;當n=5時,γgr3(T)-γr3(T)=5-3=2;當n≥6時,γgr3(T)-γr3(T)=6-3=3.如果樹T的直徑至少為3,則由命題1和2知,γgr3(T)-γr3(T)≤2且等式成立當且僅當T=S1,t(t≥3)或T∈Π.定理1得證.

3 結 語

本文研究了圖的經典控制數(shù)的一個衍生控制參數(shù),即全局彩虹控制數(shù)問題.通過對樹的結構分析,刻畫了γgr3(T)-γr3(T)=2和γgr3(T)-γr3(T)=3成立的所有樹T,推廣了已知結果.期望在今后的研究工作中能夠進一步刻畫γgr3(T)-γr3(T)=1成立的所有樹T.