次擴散過程驅(qū)動下的歐式障礙期權(quán)定價

趙 蘋,郭志東

(安慶師范大學(xué)數(shù)理學(xué)院,安徽 安慶 246133)

0 引言

期權(quán)是重要的金融衍生產(chǎn)品之一.最為經(jīng)典的期權(quán)定價模型是由BLACK和SCHOLES在1973年建立的Black-Scholes模型[1].在經(jīng)典的Black-Scholes期權(quán)定價模型中,標(biāo)的資產(chǎn)價格變化的隨機驅(qū)動源是布朗運動.布朗運動無法刻畫標(biāo)的資產(chǎn)價格變化的常值周期性特征,標(biāo)的資產(chǎn)價格變化的這一特征在無交易或交易量極小的新興市場中是很常見的.為了彌補這一缺陷,MAGDZIARZ[2]率先將次擴散布朗運動應(yīng)用到期權(quán)定價問題,建立了次擴散機制下的Black-scholes模型,并給出了模型下歐式看漲期權(quán)的定價公式.不同于布朗運動和分?jǐn)?shù)布朗運動,次擴散布朗運動可以很好地刻畫標(biāo)的資產(chǎn)價格變化的常值周期性特征.自此以后,許多學(xué)者研究并建立了次擴散機制下的若干期權(quán)定價模型.例如,KRZYZANOWSKI等[3]在已建立的次擴散Black-scholes方程基礎(chǔ)上,運用有限差分法得出該模型下的數(shù)值計算結(jié)果.WANG等[4]建立了次擴散機制下帶交易成本的Black-scholes模型,得出歐式期權(quán)的定價公式及平價公式.GUO[5]建立了次擴散機制下Merton期權(quán)定價模型,得出該模型下歐式期權(quán)的顯示定價公式,并給出了相應(yīng)的數(shù)值模擬結(jié)果.GUO等[6]建立了次擴散機制下幾何亞式期權(quán)定價模型,給出了亞式期權(quán)的定價公式.

障礙期權(quán)是一種新型奇異期權(quán),它的最終收益與原生資產(chǎn)在到期日的價格有關(guān),還與原生資產(chǎn)在規(guī)定時期內(nèi)的價格能否達(dá)到某固定水平有關(guān)[7].障礙期權(quán)的定價問題也受到許多學(xué)者的廣泛關(guān)注.MERTON[8]在經(jīng)典期權(quán)定價模型下,給出了歐式向下敲出看漲期權(quán)的解析公式.RUBINSTEIN等[9]通過變量換元和因式推導(dǎo)的方法,給出了標(biāo)準(zhǔn)障礙期權(quán)的定價公式顯示解.HEYNEN等[10]研究了彩虹障礙期權(quán)的定價問題,利用有限差分法給出了彩虹障礙期權(quán)的定價近似解.鄭祥等[11]基于幾何布朗運動下Merton模型的解析解和蒙特卡洛算法,建立了符合國內(nèi)金融市場的交易策略,結(jié)合實證得到了障礙期權(quán)的有效對沖.張素梅[12]研究了隨機波動下的障礙期權(quán)定價,通過非均勻有限差分的方法,給出了求解障礙期權(quán)的穩(wěn)健性模型.韋才敏等[13]構(gòu)建了混合分?jǐn)?shù)布朗運動下的歐式障礙期權(quán)定價模型,結(jié)合換元法和偏微分方程理論,給出了障礙期權(quán)的定價顯示解.溫鮮等[14]構(gòu)建了分?jǐn)?shù)布朗運動下的美式障礙期權(quán)定價模型,通過二次近似法給出了美式下降障礙期權(quán)的近似解和邊界價格.

在上述文獻(xiàn)中,都沒有考慮次擴散機制下的障礙期權(quán)定價問題.本文將標(biāo)的資產(chǎn)常值周期性特征納入障礙期權(quán)定價模型中,建立次擴散驅(qū)動下的歐式障礙期權(quán)定價模型.

1 次擴散過程

次擴散幾何布朗運動為Sα(t)=S(Tα(t)),母過程S(t)為幾何布朗運動,有

dS(t)=rS(t)dt+σS(t)dB(t),

其中,r,σ為常數(shù),dB(t)表示標(biāo)準(zhǔn)布朗運動.Tα(t)表示逆α-穩(wěn)定從屬過程,且α∈(0,1),有

Tα(t)=inf{τ>0:Uα(τ)>t},

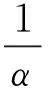
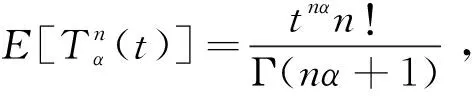
下面在次擴散布朗運動的基礎(chǔ)上,建立次擴散機制下歐式障礙期權(quán)的定價模型.

2 次擴散過程驅(qū)動下的障礙期權(quán)定價模型

考慮金融市場上存在兩種資產(chǎn),無風(fēng)險資產(chǎn)和風(fēng)險資產(chǎn)St(標(biāo)的資產(chǎn)).標(biāo)的資產(chǎn)價格無須支付紅利,到期日為時間T,敲定價格為K,障礙值為B.并假設(shè):

(i)標(biāo)的資產(chǎn)價格St滿足次擴散布朗運動:

dSt=rStd(Tα(t))+σStdB(Tα(t)),

(1)

其中,r,σ分別表示標(biāo)的資產(chǎn)的預(yù)期收益率和波動率.

(ii)市場不存在套利機會.

(iii)交易是連續(xù)的,允許賣空買空.

(iv)不支付交易費和稅收.

在上述假設(shè)條件下,可以得到歐式障礙期權(quán)的價格所滿足的偏微分方程.

定理1 記Vt=V(St,t)為歐式障礙期權(quán)的價格,則在上述假設(shè)條件下,可以得到歐式障礙期權(quán)的價格Vt=V(St,t)滿足偏微分方程:

證明 由Taylor展開式及假設(shè)條件(i),有

進(jìn)而,

構(gòu)造投資組合Π=V-ΔS(Δ是原生資產(chǎn)的份額),在[t,t+dt]時間段內(nèi)有

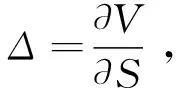
(2)

由假設(shè)Π在(t,t+dt)是無風(fēng)險的,dΠ=rΠdt,聯(lián)立式(2)可得

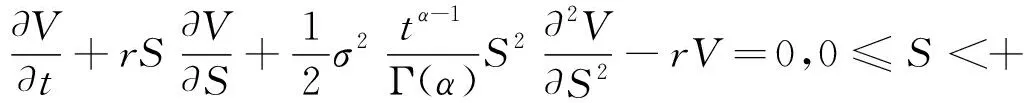
則定理1得證.

記P(S,t)為歐式下降敲出看跌障礙期權(quán)的價格,由定理1可知,P(S,t)滿足下面的偏微分方程定解問題:

(3)

求解上述偏微分方程定解問題,可得歐式下降敲出看跌障礙期權(quán)的價格.

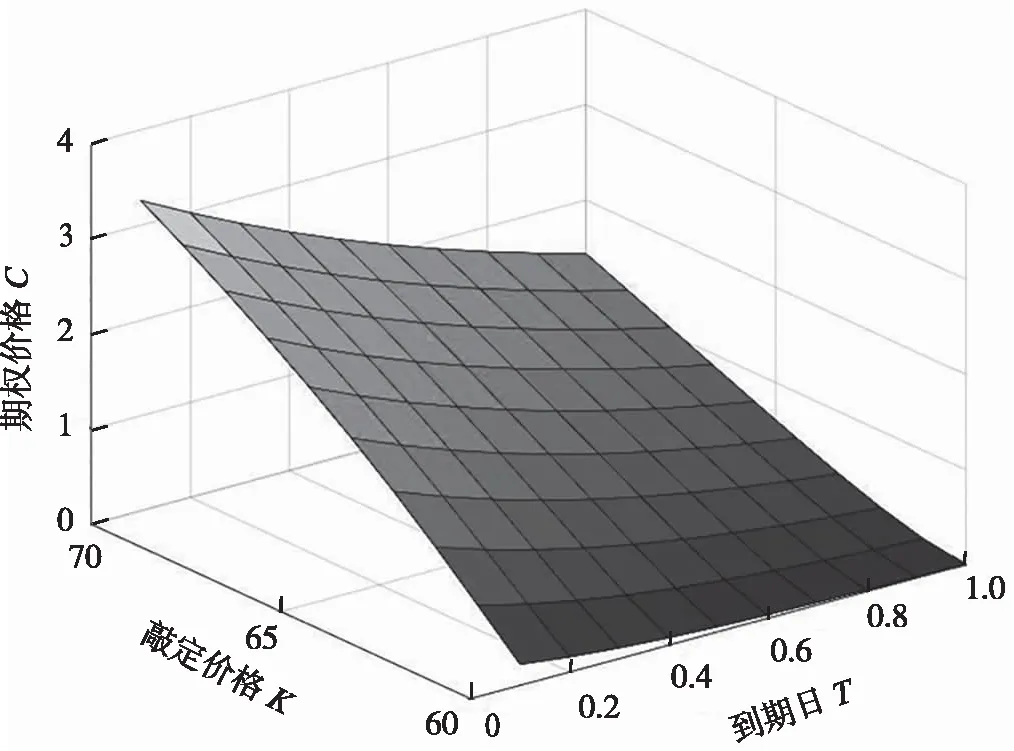
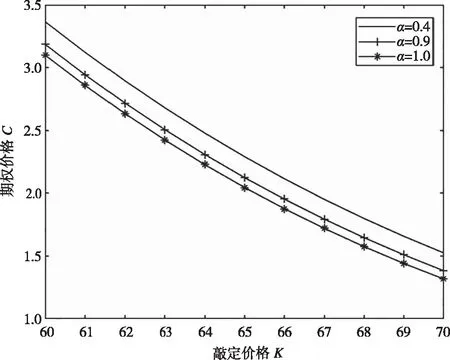
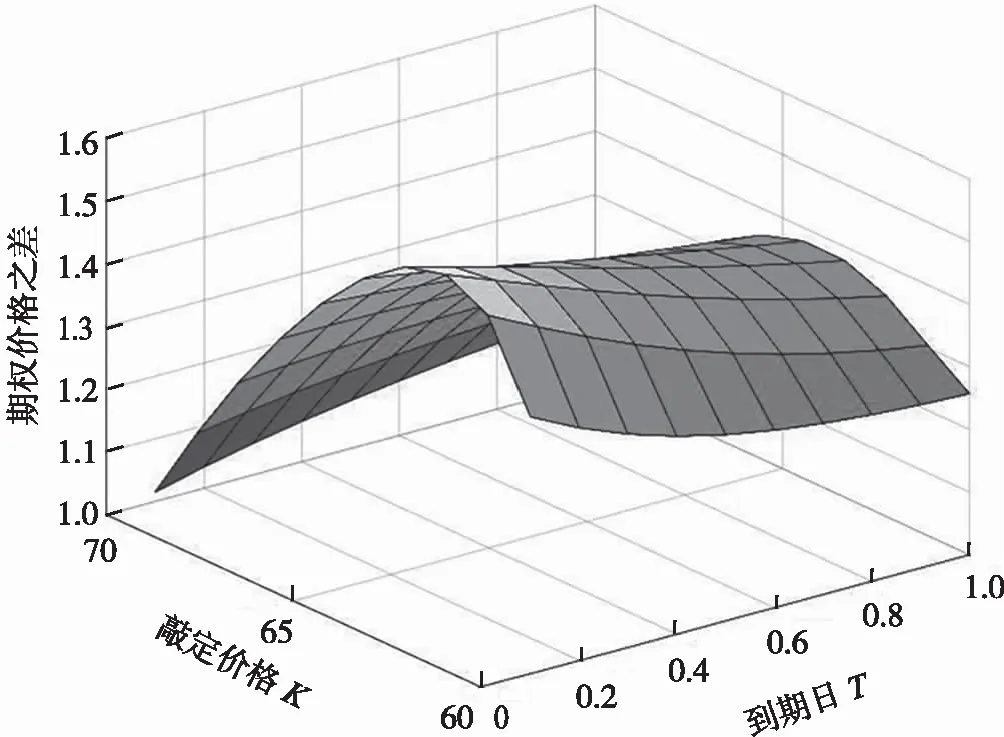
定理2 當(dāng)標(biāo)的資產(chǎn)的價格滿足式(1)時,收益函數(shù)為(K-S)+I{B

(4)

其中,

且N(·)表示標(biāo)準(zhǔn)正態(tài)的累積分布函數(shù).

證明 為求解偏微分方程定解問題(3),構(gòu)造如下變換:

代入方程可得

取

整理可得

(5)

則定解問題(3)轉(zhuǎn)化為下面的定解問題:

由熱傳導(dǎo)方程理論可知,上面定解問題的解可表示為

(6)

令

要使邊界條件ω(a(t),τ)=0成立,f(ξ)應(yīng)為奇函數(shù),因此,

且

代入公式(6)得到

整理得到

進(jìn)一步換元變換可得

其中,d1,d2,d3,d4,d5,d6,d7,d8如式(4)所示.

同理,記C(S,t)為歐式下降敲出看漲障礙期權(quán)價格,運用類似的方法可得.

定理3 當(dāng)標(biāo)的資產(chǎn)的價格滿足(1)時,歐式下降敲出看漲障礙期權(quán)價格為

其中,d1,d3,d5,d7如式(4)所示.

證明,類似于定理2.

3 數(shù)值模擬

本節(jié)將給出相關(guān)的數(shù)值計算結(jié)果.參數(shù)取值r=0.05,σ=0.3,S0=60,B=40,α=0.8,隨著敲定價格K和到期日T的取值變化,得到如圖1所示的圖形.

圖1 不同價格和到期日對期權(quán)價格的影響

從圖1可以看出,隨著敲定價格K的增加,期權(quán)價格不斷增加,當(dāng)?shù)狡谌誘不斷增加時,期權(quán)價格在逐漸減小.次擴散參數(shù)的不同取值對價格的影響如圖2所示.從圖2可以看出,參數(shù)α取不同值時,隨著α值的增加,期權(quán)的價格逐漸減少.

圖2 次擴散參數(shù)的不同取值對價格的影響

經(jīng)典歐式障礙期權(quán)價格與次擴散布朗運動下的期權(quán)價格差價如圖3所示.從圖3可以看出,當(dāng)敲定價格固定,幾何布朗運動下的歐式下降敲出看漲障礙期權(quán)價格要高于次擴散布朗運動下的歐式下降敲出看漲障礙期權(quán)價格,隨著敲定價格的增加,兩種模型下的期權(quán)價格之差逐漸減少.

圖3 經(jīng)典歐式障礙期權(quán)價格與次擴散布朗運動下的期權(quán)價格差價

4 結(jié)語

現(xiàn)有的期權(quán)定價模型通常選用布朗運動或分?jǐn)?shù)布朗運動作為期權(quán)定價的隨機驅(qū)動源.然而,無論是幾何布朗運動還是分?jǐn)?shù)布朗運動,都無法描述標(biāo)的資產(chǎn)價格變化的常值周期性特點.本文將標(biāo)的資產(chǎn)常值周期性特征納入期權(quán)定價中,建立了次擴散機制下的歐式障礙期權(quán)的定價模型,給出了模型下歐式障礙期權(quán)定價的顯示定價公式及相關(guān)數(shù)值計算結(jié)果.數(shù)值計算結(jié)果表明,相同參數(shù)下次擴散機制下歐式下降敲出看漲障礙期權(quán)的價格要低于其在幾何布朗機制下的價格.