Magnetic ground state of plutonium dioxide: DFT+U calculations
Yue-Fei Hou(侯躍飛) Wei Jiang(江偉) Shu-Jing Li(李淑靜)Zhen-Guo Fu(付振國) and Ping Zhang(張平)
1Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
2Beijing University of Chemical Technology,Beijing 100029,China
3School of Physics and Physical Engineering,Qufu Normal University,Qufu 273165,China
Keywords: strongly correlated system,magnetic ground state,noncollinear,MagGene
1.Introduction
Some of the actinide oxides (XO2,X= U, Np, Pu,Am,etc.), as typical strongly correlated systems, normally form the cubic fluorite structure with anFmˉ3m(225) space group.[1]These series of compounds are either Mott insulators or charge-transfer insulators and they provide outstanding platforms to study the properties of localized 5f electrons.Now that the 5f orbits are partially filled in these systems,nonzero magnetic moments can be naturally imagined.Meanwhile,with the presence of spin-orbit coupling(SOC)and cubic crystal field effect,the magnetism of these actinide oxides is expected to be even abundant and complex.
Years before, the magnetic ground states of these actinide oxides had been a fundamental topic causing much discussion.[2]Today experimental evidences of the triple-k(3k)-type magnetic ground states for UO2and NpO2have been reported in literatures.[3-9]However, different from the Curie-Weiss susceptibility found in UO2[10]and NpO2,[11]a temperature-independent susceptibility[12]is observed in PuO2.What is more,the nuclear magnetic resonance(NMR)experiments[13-15]imply no magnetic order occurred in PuO2at low temperature.Surprisingly, a simple crystal field(CF) theory successfully explains the non-magnetic picture of PuO2.[2]In response,inelastic neutron scattering spectrum(INSS)confirms the transition from theΓ1singlet state to theΓ4triplet state (i.e., the CF ground state to the first excited state) of PuO2with a peak at 123 meV.[16]Based on a local density approximation(LDA)calculation to density functional theory(DFT),[17]theΓ1state is 99 meV lower than theΓ4state.Another LDA calculation combined with exact diagonalization(LDA+ED)of the Anderson impurity model[18]suggests a gap of 126 meV between the two states.These theoretical results are considered to be in reasonable agreement with the INSS.Until here, the nonmagnetic ground state of PuO2seems to be clear.However, one abnormal issue is that the experimental susceptibility is much smaller(about 50%)than that of one would expect from the van Vleck coupling of theΓ1with theΓ4.[2,12,16,18]Although the multiconfigurational wave function calculations[19]reproduces the experimental susceptibility of PuO2, more discussions are required to ensure this achievement.Anyway, the magnetism of PuO2needs more investigations from both experimental measurements and theoretical modeling.
In fact, PuO2is a challenging system to investigate in experiments duo to its nucleonic radioactive decay and the inhomogeneity of the samples.[20-23]As a result, a series of computational works have been carried out to understand the ground state properties of this system in-depth.Before further simulation of its properties, a reasonable magnetic model for the ground state of PuO2is firstly required.For instance, by assuming a simple nonmagnetic (NM), ferromagnetic (FM) or collinear antiferromagnetic (AFM) ground state,many fundamental physical characters of PuO2,including electronic,[24-28]optical,[27,29]thermodynamic,[27,30]lattice dynamic,[24,31]and surface[24,32-34]properties,have been studied through first-principles calculations.Among them,DFT-based calculations are especially popular to study PuO2due to its balance between accuracy and economy.
It has been revealed that conventional DFT or even DFT+Ucalculations tend to provide rather an FM or a collinear AFM ground state[24-28]than the recognized nonmagnetic state by comparing their free energies.To theoretically obtain a nonmagnetic ground state, the modified LDA calculation[18]seems to succeed while CF parameters obtained from the experiment are applied which makes the computational work not totallyab initio.On the other hand,it may also be meaningful to leave out the energy difference between magnetic or nonmagnetic states and directly impose a nonmagnetic state in the calculation.For instance, by taking into account SOC and HubbardUmodifications,DFT+Ucalculations for the nonmagnetic PuO2are performed[35,36]and useful results are gained.Despite all this, the consistency between the real ground state and the simulated ground state is of great significance to the applicability of DFT.Only with this robust consistency could we then safely predict other similar systems by using the DFT based methodology.Hence,the ground state of PuO2belonging to the DFT framework is required to be determined and examined carefully.Pegget al.[20]calculated the total energy of PuO2with different magnetic structures and found a noncollinear longitudinal 3kAFM ground state by using HSE06 hybrid density functional.Nonmagnetic state matches much higher energy than magnetic states in their calculations.The origin of the inconsistency occurred in a series of DFT-based studies[24-28]needs more investigations.
In this work,a systematic DFT+Ucalculation for determining the magnetic ground state of PuO2is performed.The SOC effect is included explicitly in our calculations, which has been proved to be an essential effect in PuO2.[35,36]Therefore, the noncollinear magnetic algorithm is employed here.HubbardUmodel is used to describe the Coulomb interactions between correlated electrons.The whole process of this work can also be adopted to study other actinide oxides,such as UO2, NpO2, AmO2,etc.The local density approximation (LDA),[37]the generalized gradient approximation(PBE here),[38]and the strongly constrained and appropriately normed(SCAN)[39]exchange-correlation functionals are applied in our calculations, respectively.The three exchangecorrelation functionals which contain different physical information are belonging to three different levels of the Jacob ladder.[40]A pureab initioDFT+Ucalculation without taking into account any experimental parameters is performed here.
2.Computational method
We employ the Viennaab initiosimulation package(VASP)[41]code to achieve DFT+Uscheme.The projected augmented wave (PAW) method[42-44]with the frozen-core approximation is used.The first Brillouin zone of the unit cell is sampled by 6×6×6k-point mesh.The cut-off energy of the plane wave basis for electron wave function is chosen as 520 eV.We have carefully checked the convergence ofk-point mesh and cut-off energy.Atomic structures are fully relaxed until the Feynman-Hellman force on each atom is less than 0.01 eV/°A.The convergence accuracy of the energy for selfconsistent calculation is 10-7eV.
In the DFT+Ustudy, screened Coulomb parameterUand Hund exchange parameterJare significant.Many efforts have been devoted to determine theUandJin PuO2.By scanning lattice constant,[24,26,27]bulk modulus,[24,26]band gap,[20,27]and magnetic moment[20]in variousUandJ, the best combination of the two parameters can be chosen to match properties observed in experiments.Here, we adopt a scheme from a first-principles calculation[45]which points out the significance of electronic correlation on O-p orbits in actinide oxides.We note that a nonzeroUfor O-p does not change the properties of PuO2qualitatively.The electronic correlation on O-p orbits only slightly modifies the electronic structure (see supporting information S5).Thereby,U=4.7 eV andJ=0.6 eV for Pu-5f orbits andU=3.0 eV andJ=0 eV for O-p orbits are applied.Multiple values ofUfor Pu-f electrons have been used in the literature varying from 4 eV to 6.5 eV.[18,20,27,34-36]As a precaution,a test before further discussions is made and we find that the energy order of the magnetic structures keeps unchanged whenUvaries in the range of 3 eV to 7 eV.An unreasonable metallic ground state which is contrast to the experimental insulating state occurs only whenUis quite small(roughly less than 0.5 eV).
We make use of the approach originated from Liechtenstein’s[46]DFT+Umethod for the main part of the calculation.The generalized form of the energy functional is given by
whereρσ(r)is the charge density,andnσis the trace of density matrix for spinσ(↑or↓).The first term on the right-hand side represents standard DFT functional.It can be substituted by LDA, PBE, and SCAN functionals in our work.UandJaffect the total energy independently in the double counting term written as
wheren=n↑+n↓denotes the total occupation number of both spin-up and spin-down electrons.In addition,Dudarev’s simplified DFT+Uapproach is also employed as a comparison,which will be discussed in Subsection 3.4.
3.Results
3.1.Magnetic structures in the cubic fluorite atomic structure
The Bravais lattice of PuO2is face centered cubic(FCC)with one Pu atom and two O atoms in the primitive cell.In order to produce possible 3kmagnetic structures,the conventional cell (Pu4O8) of PuO2with the simple cubic (SC) lattice is adopted, as shown in the right top of Fig.1.The four first-nearest Pu ions in this unit cell form a regular tetrahedron before relaxing the atomic structure with an imposed magnetic structure.Because of the periodic boundary condition,all second-nearest Pu ions are naturally in FM order.We cautiously do a test and prove that the unit cell adopted here is convincing to describe the magnetic ground state of PuO2(see more details in supporting information S1).The magnetic moments of O ions are ignored.
Based on former ideas,[2,20]typical magnetic structures are listed in Fig.1.The superiority of our work is that three more collinear magnetic structures as shown in Figs.1(e),1(f),and 1(j) are involved in the calculations.The three magnetic structures are the transformations of transverse 1kAFM or longitudinal 1kAFM structures and they are discussed for the first time.With the existence of strong SOC and remarkable CF effect,[2]the magnetic anisotropy is very likely to play an important role in the formation of the magnetic ground state.As a result,we classify the magnetic structures into 001,011,and 111 structures whose magnetic moments point along〈001〉,〈011〉, and〈111〉, respectively.Details are shown in supporting information S2.

Fig.1.The atomic structure of cubic fluorite PuO2 (on the right top) and typical collinear and noncollinear magnetic structures [(a)-(l)].Pu atoms represented by the large balls are shown to form magnetic structures.Arrows on the atoms represent magnetic moment vectors.Each color of the arrows corresponds to one specific vector of each magnetic structure.Orientations of the magnetic moments are along(a)-(c)〈001〉,(d)-(h)〈011〉,and(i)-(l)〈111〉.The magnetic structures shown in panels (a), (d), and (i) are FM structures while the others are the so-called AFM structures with the label“AFM”omitted for simplicity.
3.2.Determination of the magnetic ground state
The atomic structure of actinide oxides tends to produce Jahn-Teller (JT) distortion when imposing a magnetic structure.For instance, the realistic UO2single crystal lowers the symmetry toPaˉ3 space group at low temperature beneath the N′eel temperature.The distortion on O atoms of about 0.014 °A along〈111〉has been observed within a transverse 3kmagnetic structure.[3]This feature can also be faithfully reflected by our calculations performed on PuO2.The space groups of the distorted crystal with different imposed magnetic structures are listed in Table 1.One can find that the nonmagnetic state and the longitudinal 3kmagnetic state remainFmˉ3mspace group recommended by the experiments.The transverse 3kmagnetic state of PuO2is ofPaˉ3 symmetry.The distortion of O atoms is carefully calculated by employing the three functionals to be around 0.015 °A along〈111〉.This phenomenon is very similar to that in UO2.Meanwhile, imposing this distortion is far not enough to change the intrinsic magnetic ground state of PuO2.Details can be found in supporting information S3.It indicates that the possible atomic distortion in actinide oxides at low temperature is rather a consequence than an motive force of the magnetic structure for the ground state.Dudarevet al.have studied the JT distortion of UO2through LSDA+Ucalculations before.[47]Their conclusions and ours agree well with each other.
Lattice constant of PuO2calculated by LDA, PBE,SCAN,and HSE06[20]are compared in Fig.2(a).One can see that different imposed magnetic structures only slightly modify the lattice constant.The notable distinction is contributed from the exchange-correlation functional.On one hand,LDA underestimates the lattice constant, while PBE (GGA) overestimates the lattice constant.This is consistent with prior LDA+Uand GGA+Uresults.[26]On the other hand,HSE06 and especially SCAN give out pretty good prediction of the lattice constant.
The total magnetic moment of a Pu ion is composed of both spin moment and orbital moment originated from 5f electrons.Large magnetic dipole moment of the Pu ion is recommended as shown in Fig.2(b).The magnetic moments of the Pu ions for different magnetic structures are approximately invariant in an acceptable range.This can be thought as a consequence of both strong SOC and on-site Coulomb interaction.These two effects dominate the local electronic configuration of the magnetic ions and tend to keep the magnetic moment unchanged.When rotating the local moments, only the electron-electron interactions between different sites are notably affected.This kind of interactions is relatively weak.As a result, different magnetic structures hardly make huge difference on the local magnetic moments of the Pu ions.

Table 1.Space group of PuO2 with the magnetic structures imposed.These symmetry properties are only based on the simulated atomic structures.Any atomic distortion less than 10-3 °A is neglected.LDA,PBE,and SCAN as well as HSE06[20] give the consistent results here.
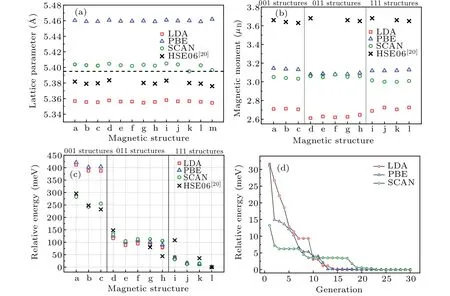
Fig.2.(a)Lattice constant of PuO2 with different magnetic structures calculated by LDA(red squares), PBE(blue triangles), SCAN(green circles),and HSE06(black crosses).[20]In the abscissa,letters a-l correspond to magnetic structures shown in Figs.1(a)-1(l),and m represents the nonmagnetic situation.Black dashed line denoting the experimental lattice constant from x-ray diffraction.[54] (b)The calculated magnetic moment of a single Pu ion with different magnetic structures imposed.Magnetic structures belonging to 001,011,and 111 types are separated in three regions.(c)Relative energy of PuO2 with different magnetic structures.Nonmagnetic state is not shown as it matches too much higher energy.The total energy of the magnetic ground state for each exchange-correlation functional is set to 0.(d)The lowest energy found in each generation relative to the energy of the magnetic ground state during the MagGene process.
The total energy of the Pu4O8unit cell varies in a range of about 420 meV among the magnetic structures as shown in Fig.2(c).The energy of the nonmagnetic state in our calculations is almost about 4 eV higher than the other magnetic states no matter which exchange-correlation functional is applied (LDA, PBE, SCAN, as well as HSE06[20]).Thereby,we do not discuss the simulated nonmagnetic states in this work.According to the results for LDA, PBE, and SCAN,the orientation of the local magnetic moments dominate the total energy as we expected.The 111 structures are normally favored in energy and the 011 structures take higher energy than the 111 structures.Finally,the 001 structures cause much higher energy than both 111 structures and 011 structures.Furthermore, the FM configuration(i.e., structures a, d, and i)is also less stable than AFM configuration in a group of structures whose magnetic moments point along the same crystallographic direction family (for〈001〉,〈011〉, and〈111〉, respectively).In the case of HSE06,[20]things are a little different.Referring to Fig.2(c),relative energy of the magnetic structures shows a similar trend to our applied three functionals.However,we notice that the departure in energy between FM structures and AFM structures is larger.From this point of view,HSE06 hybrid functional may take more highly of the interactions from f-p super-exchange and f-f exchange than the other three functionals.Anyway,the longitudinal 3kAFM structure to be the magnetic ground state of PuO2is confirmed by LDA,PBE,SCAN,and HSE06 consistently.
When SOC is involved in DFT+Ucalculations,total energy is not only the functional of the charge density but also the functional of the magnetization density when no external field is imposed.[48]The magnetic moment of an ion on siteiis the integral of the magnetization density inside the Wigner-Seitz(WS)radius given by
In our unconstrained DFT+U+SOC calculations realized by VASP,[41]the orientation of the initial local magnetic moment is still needed to be artificially set.Usually, to search the ground state in the subspace of magnetic ordered states,several typical high-symmetry magnetic structures are at least needed to be considered (refer to Fig.1).In this way, the number of considered magnetic structures is limited.To exclude any other possible magnetic structures with lower energy which might be missed,we expand the searching range to a larger space.We firstly let the local moments in the unit cell rotate freely.Random magnetic structures can be then gained at different moments.Meanwhile, to overcome the blindness during the calculations, the MagGene code based on the genetic algorithm is applied to locate the magnetic ground state efficiently.Details can be found in supporting information S4 and also the paper from Zhenget al.[49]At the beginning of the searching process for PuO2, sixteen random magnetic structures are generated.Following that, five structures with the lowest five energies are chosen as parents for the next generation.Based on these parents, six mutation structures and two crossover structures are produced.The last part of the next generation is eight (16-6-2=8) random structures,which help to get rid of the local minima of the energy surface and keep the size of population unchanged.The lowest energy found in each generation is shown in Fig.2(d).When a thirty generations’ searching is finished, the longitudinal 3kAFM ground state is found in the 19th, 22nd,and 23rd generations when LDA,PBE,and SCAN are applied,respectively.
3.3.Electronic structure of the magnetic ground state
A large unit cell of PuO2is necessary to describe the longitudinal 3kAFM ground state.The first Brillouin zone of the Pu4O8simple cubic lattice is shown in Fig.3.
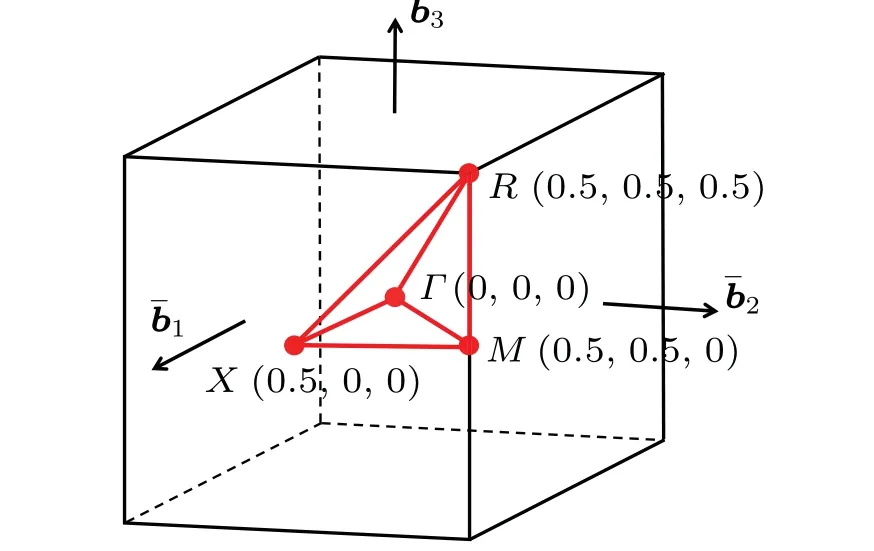
Fig.3.First Brillouin zone and high symmetry path for the simple cubic lattice of the Pu4O8 conventional cell.
We adoptΓ-X-M-Γ-R-X/M-Rhigh symmetry path[50]to describe the dispersion of the total energy.Density of states(DOS) and electronic band structures calculated by the three functionals are plotted in Fig.4.Our DFT+U+SOC calculations for the longitudinal 3kAFM ground state reasonably suggest PuO2to be a charge-transfer insulator which has been widely identified before.A strong hybridization between Pu-f and O-p orbits is identified.This feature explains why taking into account the correlation on O-p orbits is necessary.Similar to the magnetic ground state calculated by HSE06,[20]a remarkable peak of O-p below the Fermi level in the DOS is located at about-1.1 eV.Another broad peak close to the Fermi level is actually a double peak in our calculation as shown in Figs.4(a)-4(c).One can see from the Figs.4(d)-4(f) that the direct gap of the band structure is 2.46 eV, 2.47 eV, and 2.69 eV corresponding to the LDA,PBE,and SCAN functionals.To our surprise, these values calculated from the longitudinal 3kAFM ground state are even more close to the experimental optical gap which is 2.8 eV[51]than that from the simulated nonmagnetic state(about 1.8 eV).[18,36]Hence, we trust that the longitudinal 3kAFM structure is the best approximation to model the electronic ground state of PuO2so far and it has been adopted to calculate the formation energy.[47]
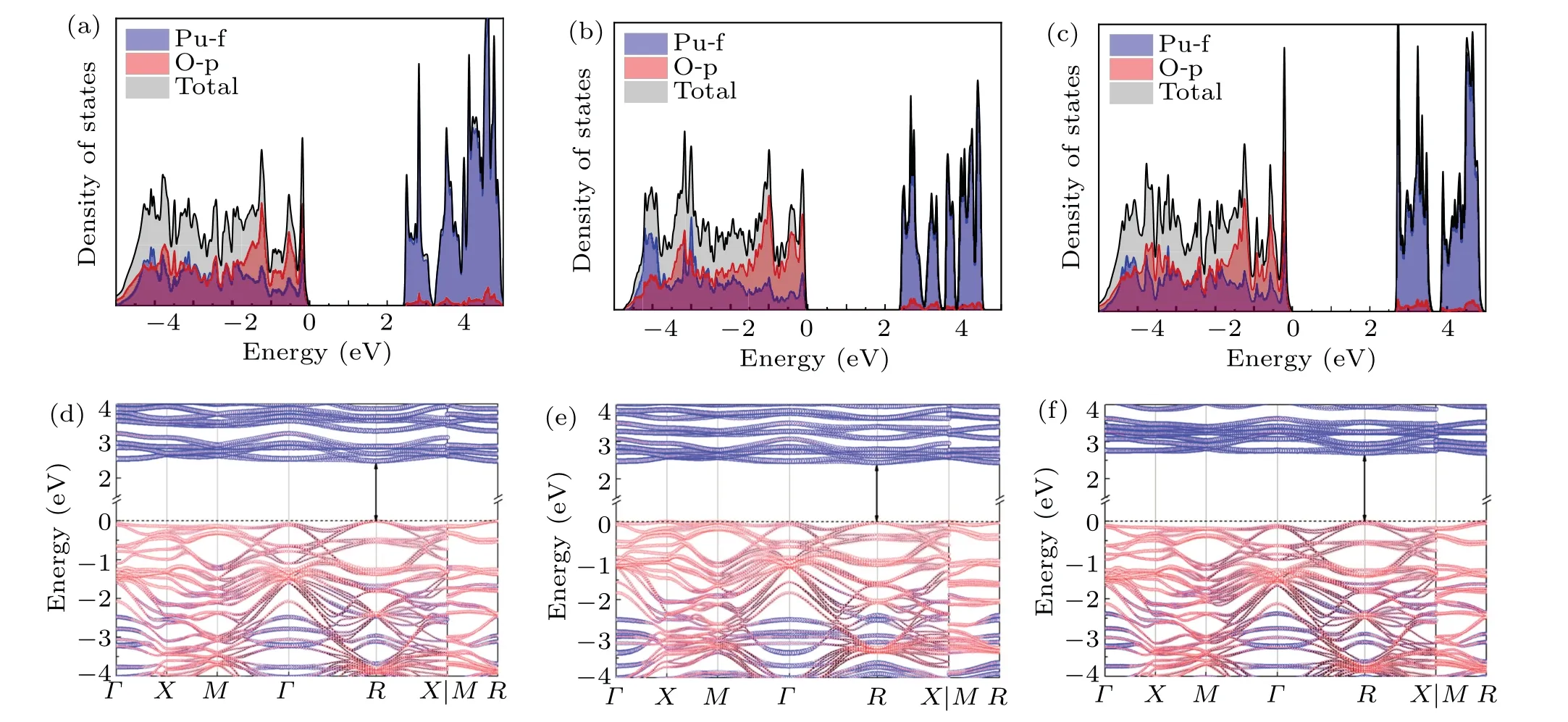
Fig.4.Electronic DOS of the longitudinal 3k AFM ground state and the corresponding band structures for LDA[(a)and(d)],PBE[(b)and(e)],and SCAN[(c)and(f)].Blue circles and red circles in panels(d)-(f)represent the contributions from Pu-f and O-p orbitals.The size of the circles shows the weight of each component.
3.4.A comparison with Dudarev’s DFT+U approach
Another widely used DFT+Uscheme based on Dudarev’s DFT+Umodel[52]is inspected here.The total energy modified by this model is given by
whereρσis the density matrix of correlated electrons with spinσ.In this simplified approach,UandJare handled in a spherically averaged form of the screened Coulomb interaction and exchange interaction.We adopt the sameUandJas used in the former Liechtenstein’s model.Total energies of different magnetic structures are calculated again,and the corresponding results are shown in Fig.5(a).We firstly find that the energy range among these structures is about 200 meV,which is only about half of that obtained by Liechtenstein’s approach.For LDA or PBE functional,the〈111〉easy axis of magnetization is reproduced and the longitudinal 3kmagnetic ground state is determined as expected.However, for SCAN functional, structures with atomic moments along〈011〉are favored in energy.
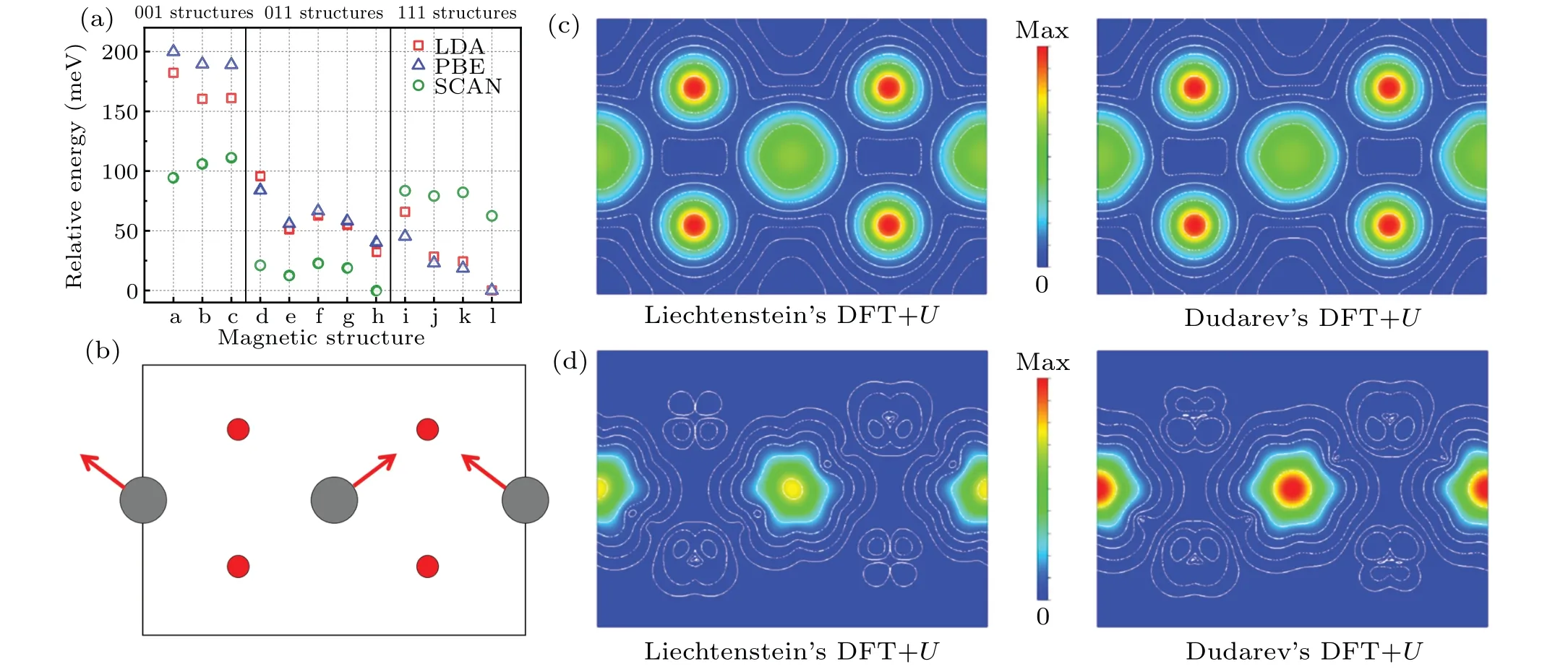
Fig.5.(a)Relative energy of PuO2 with different magnetic structures obtained from Dudarev’s DFT+U approach.In the abscissa,letters a-l correspond to the magnetic structures shown in Figs.1(a)-1(l).The total energy of the magnetic ground state for each exchange-correlation functional is set to 0.(b)The(1-1 0)section of PuO2 crystal with longitudinal 3k AFM structure.Red arrows represent magnetic moments.(c)The charge density plot on the(1-1 0)section calculated by Liechtenstein’s DFT+U approach and Dudarev’s DFT+U approach.(d)The magnetization densities plot on the(1-1 0)section calculated by Liechtenstein’s DFT+U approach and Dudarev’s DFT+U approach.The direction of the magnetization vector on each grid is not shown for simplicity.
Moreover, the preference for AFM structures in energy is invalid in this case.As shown in Fig.5(a), the 001-FM structure is the most stable among 001 magnetic structures.In Dudarev’s DFT+Uapproach, it is abnormal for SCAN to get such results which are contrary to LDA and PBE, especially when a consistent conclusion is arrived with Liechtenstein’s DFT+Uapproach for all three exchange-correlation functionals.
We also would like to compare the ionic states of the longitudinal 3kmagnetic structure calculated by Liechtenstein’s DFT+Uapproach and Dudarev’s DFT+Uapproach.The charge densities of both approaches with SCAN adopted are represented in Fig.5(c).There is only slight difference in the two charge densities, which is originated from Pu ions.However,the magnetization density emphasizes a remarkable distinction.By calculating the integral of the magnetization density inside the Wigner-Seitz radius of Pu, we obtain the magnetic moment to be 3.00μBand 3.72μBfrom Liechtenstein’s approach and Dudarev’s approach.From the distributions of the magnetization densities as shown in Fig.5(d),we notice that two different ionic states are gained from these two DFT+Uapproaches although the same values ofUandJare employed.The corresponding occupation matrices for Pu-f orbits are also shown in supporting information S6 to numerically confirm this character.
4.Discussion
We treat PuO2as a standard computational model of actinide oxides with half-filled 5f electrons and expect the methodology here to be expanded to other actinide oxides.Previous DFT calculations have illustrated that a simple collinear magnetic model without SOC is meaningful to describe a series of properties of PuO2as long as a HubbardUmodification is considered.However,this framework of computation is too rough for magnetic properties.With the existence of the on-site CoulombUand strong SOC, the way of occupation for Pu-5f orbits takes on great responsibilities for the total energy.On our calculated NM state, the electronic configuration of the 5f electrons remarkably differs from the magnetic states and that’s why it has much higher energy.Based on the same local occupation for Pu-5f orbits, the total charge density and the magnetization density can be once again modified by a specific magnetic structure.According to our simulations,the total energies slightly fluctuate among different magnetic structures in a range of dozens of meV per PuO2.
We point out that the typical magnetic structures here combined with their energies can be used to fit an effective pseudo spin Hamiltonian as proposed before.[53]Since the spin-spin interactions in actinide oxides are complex, multiple model parameters have been taken into account in the Hamiltonian.As a result, for the accuracy of the fitting job,the amount of the used magnetic structures should not be too small.Meanwhile, the magnetic structures ought to be with the approximately equal local electronic occupation for Pu-5f orbits.Once any magnetic structures with definitely different ionic states are involved in the fitting job, the fitted parameters would be unphysical and meaningless.At least for PuO2,the magnetic structures simulated by our DFT+Umethod are perfect samples for a high-quality fitting.
Furthermore,there are at least two possible reasons need to be noticed for understanding the inconsistency of the ground states between DFT calculation and experiments for PuO2.The first reason is that the longitudinal 3kmagnetic state obtained here may be a metastable state which corresponds to a local minima on the energy surface.To validate this, an occupation control procedure for the local electrons should be a promising method to completely search the subspace of the electronic configuration.Another reason is that the physical information of the computational model may be not compatible with the real system.If so, additional modification is required for DFT based calculations to PuO2.Anyway,the origin of this inconsistency needs more intriguing investigations.An universalab initiocomputational framework is needed to reasonably describe the real ground state of actinide oxides based on DFT+Umethod.We will leave this issue to our long-term work.
5.Conclusions
We studied the magnetic ordered states of PuO2by using DFT+Umethod with SOC included.The LDA, PBE, and SCAN exchange-correlation functionals are applied, respectively.The typical magnetic structures in the cubic fluorite crystal structure are classified and labeled.The JT distortions are simulated, which can be seen as an appendage of the imposed magnetic structure.The orientations of the local moments in the crystal environment are found to play an important role in the contribution to the total energy.Beyond the usual searching procedure of the magnetic ground state, the MagGene code based on the genetic algorithm is employed to ensure the longitudinal 3kAFM ground state recommended by all the three functionals.After that, the electronic structure of the magnetic ground state is discussed.According to our calculations,PuO2is predicted to be a charge-transfer insulator, whose optical gap agrees well with the experimental value.We believe that the longitudinal 3kAFM structure should be a good approximation to model the magnetic ground state of PuO2.All these results obtained here are in reasonable agreement with that obtained by using a hybrid functional in the prior computational work.Finally, we notice a divergence between Liechtenstein’s DFT+Uapproach and Dudarev’s DFT+Uapproach when both are applied to PuO2.This phenomenon occurs only when SCAN exchangecorrelation functional is adopted.
Acknowledgements
Project supported by National Natural Science Foundation of China,(Grant No.12104034).
We thank professor Fa-Wei Zheng from the School of Physics of Beijing Institute of Technology for his advice to this work.We also thank professor James T.Pegg from Department of Chemistry of University College London for his useful discussion with us.
- Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA

