Rogue waves of a(3+1)-dimensional BKP equation
Yu-Qiang Yuan(袁玉強) Xiao-Yu Wu(武曉昱) and Zhong Du(杜仲)
1Department of Mathematics,China University of Mining and Technology(Beijing),Beijing 100083,China
2School of Science,Beijing Forestry University,Beijing 100083,China
3Department of Mathematics and Physics,North China Electric Power University,Baoding 071003,China
Keywords: (3+1)-dimensional BKP equation, Kadomtsev–Petviashvili hierarchy reduction, interaction,rogue wave,lump
1. Introduction
Since nonlinear waves have extensive applications, such as the evolution of optical pulse and water wave packet, researches of the nonlinear waves have been attractive in the optical fibers,fluids,and plasmas.[1–3]The physical systems relating to those nonlinear waves have been described via those nonlinear evolution equations (NLEEs) such as the nonlinear Schr¨odinger equation,the three-wave resonant interaction system, the Kadomtsev–Petviashvili(KP)equation, the longwave-short-wave resonant interaction system,the Ito equation,and the Fokas–Lenells equation.[4–7]The NLEEs play a critical part in explaining and handling problems in the fields of experiment and engineering.[8–10]Among these models,studies of the high dimensional NLEEs are concentrated to investigate the rich nonlinear waves interactions.[11–15]
In this paper, we will investigate a (3+1)-dimensional BKP equation,[16–20]

whereuis an analytic function of the scaled spatial coordinatesx,y,zand temporal coordinatet, with the subscripts denoting the partial differential derivatives. Equation (1) has been proposed as an opposite procedure on applying the linear superposition principle.[16]By using the multiple exp-function algorithm, the multiple wave solutions of Eq. (1) have been presented.[17]Rational lump solutions of Eq. (1) have been obtained via the symbolic computation.[18]The lump and linerogue wave have been derived via the KP hierarchy reduction method.[19]Certain hybrid solutions and breather solutions have been constructed.[20]
Recently, some semi-rational solutions with certain parameter constraints which reveal special resonant interaction[The resonant interaction describing a special interaction between theN-th order rational solutions andN+1 solitons,which occurs that the phase of the lump (line rogue wave)varies to infinite suddenly when such lump(line rogue wave)interacts with a soliton (based on the semi-rational solutions obtained by the Hirota method)]between the lump(line rogue wave) and soliton have been investigated via the KP hierarchy reduction[21,22]and bilinear method for the KP I equation,[23,24]the Fokas system,[25]the Davey–Stewartson(DS)I equation,[26]and some other models.[27]The resonant interaction describes the pattern in which a lump arises from one soliton and then merges with the other soliton. What is more, such the lump (line rogue wave) is localized in both space and time,which performs like a rogue wave in the higher dimensional space.
Motivated by the above interesting interaction,in this paper, we will pay our attention to investigating such resonant interaction by constructing semi-rational solutions of Eq. (1)which have not been reported before, to our knowledge. In Section 2, via the KP hierarchy reduction, we will derive the semi-rational solutions in determinant form of Eq.(1). Resonant interactions between one lump(line rogue wave)and two solitons,and between the higher-order lump and three solitons will be discussed in Section 3. Our conclusions will be presented in Section 4.
2. Semi-rational solutions of Eq.(1)
In this section, we will construct the semi-rational solutions which generate the resonant interactions between the lump (line rogue wave) and the solitons (actually the kinks)via the KP hierarchy reduction method. The basic idea of such a reduction is to make the bilinear form of the studied equation as a reduction of the KP hierarchy under certain constraints.Then we begin with the bilinear equation of Eq.(1),[19,20]

whereτis a function of the variablesxj(j=1,2,3,4). TheN-th order semi-rational solutions for KP hierarchy(4)are defined as the followingN+1 determinant:

withξ=px ?ip2y ?2p3t ?ip4z,ξ′=x ?2ipy ?6p2t ?4ip3z.The above solutions combine the rational and the exponential functions,namely,they are the semi-rational solutions in nature. Moreover,it is worth noting the following:
(I) The above semi-rational solutions will be reduced to rational solutions if the constantδjkis removed, which are exactly those solutions reported in Ref. [19] of Eq. (1). We conclude that the order of operator?p(or?p?)determines the order of rational solutions and the order of the determinant determines the number of solitons. More subtle discussions will be seen in Section 3. In addition,to obtain the interaction between the rational lump or rogue wave and solitons, we need at least two solitons. Thus,the fundamental solutions defined above should be second-order determinants.
(II) Dynamics of the rational solutions contain entirely different two cases(a stable propagating lump and a line rogue wave),consequently,the above semi-rational will lead to two interaction patterns,i.e.,the interaction between the lump and the solitons,and between the line rogue wave and the solitons.
3. Interaction between the lump (line rogue wave)and solitons
3.1. The first order lump and rogue wave
By settingN=1 in solutions(6),we derive

withR=ηη?+1/(p+p?)2,η=ξ′?1/p+p?, andc10=c20=1,c11=0. It can be seen thatζj0is always accompanied byζ?j0,which means that the imaginary part ofζj0can be removed,thus we will takeζj0as real constants hereafter.
Separating the rational and exponential functions, we rewrite the fundamental semi-rational solutions of Eq.(1)as
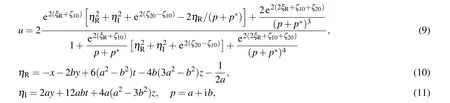
with the subscripts R and I denoting the real and imaginary parts of constants. We derive that properties of the two solitons are determined by e2(ξR+ζ10)and e2(ξR+ζ20)respectively,while the properties of the rational solutions are determined byη2R+η2I.
Based on the above solutions, we can obtain the asymptotic ofuas
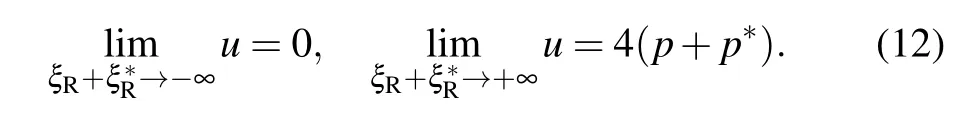
The result shows the soliton with two different asymptotic planes,which implies the above soliton is a kink one. Besides,for studying the interaction, we will takeζ10>ζ20(also in the following discussions),which makes the rational functionη2R+η2Ihold the prominent effect in the intermediate time.SinceηRandηIbear different variables, then with the different choices of parameters and planes, we will derive two different kinds of nonlinear waves: (i)whena2?3b2/=0,the rational solutions generate a lump that develops along the trajectory ofηR=0 andηI=0; (ii) whena2?3b2=0 and on thex–zplane,ηIis just a constant,thus the rational solutions generate a line wave(along the line trajectoryηR=0). Then combining with the kink solitons,we will discuss the interactions between the lump and kink solitons,and between the line rogue wave and kink solitons on thex–zplane.
In Fig. 1, we present the interaction between one lump and two kink solitons on thex–yplane.The semi-rational solutions generate a novel nonlinear wave structure which shows:(i) as the two kink solitons own the same wavenumber, they are nearly parallel with each other;(ii)the lump only exists in a short time and emerges from one kink soliton and disappears into the other one later. It should pay attention that during the interaction, such lump localizes not only in space (the nature of the lump)but also in time,which behaves like a rogue wave.Similar structure has also been revealed in Refs.[23,26]for the KP and DSI equations(that lump is called a lump-type rogue wave). In addition, as the lump will disappear finally instead of passes through the kink soliton, such interaction is quite different from that interaction pattern reported in Ref. [20].Interactions of the lump and kink solitons on they–zplane are similar to those on thex–yplane,so we will omit those analyses.
When we choosea2?3b2=0 on thex–zplane,ηIcan be seen as a constant, then solutions (9) will generate the interaction between line rogue wave and kink solitons. As shown in Figs.2,we find that(i)the two kink solitons propagate stably;(ii)the line rogue wave rises up at a certain time,reaches higher amplitude att=0, and then disappears soon; (iii) especially,the line rogue wave only exists in a segment between the two kink solitons,which implies that the line rogue wave is also localized in space. Such line rogue wave is different from that proposed in Ref.[21](which extends to infinity in space)for DSI equation. To discuss such interaction more clearly,in Fig. 3 we present some details such as the density plot of interaction att=0 and the trajectories at different positions in Fig.2(c).We compare the evolution of the interaction at different times at a fixed position atx=?5. A localized wave with a sharp shape rises between the two kink solitons(as shown in the real line in Fig.3(b))and vanishes after a short time.
In general, in this paper, we obtain two novel kinds of interactions: between the lump and two kink solitons and between the rogue wave and two kink solitons. Evolutions of the lump and the line rogue wave are both confined in time and to space(the segment between two kink solitons),which perform like a rogue wave. Thus,we show two kinds of potential rogue wave for Eq.(1)via the semi-rational solutions, which are different from that in Refs.[19,20].
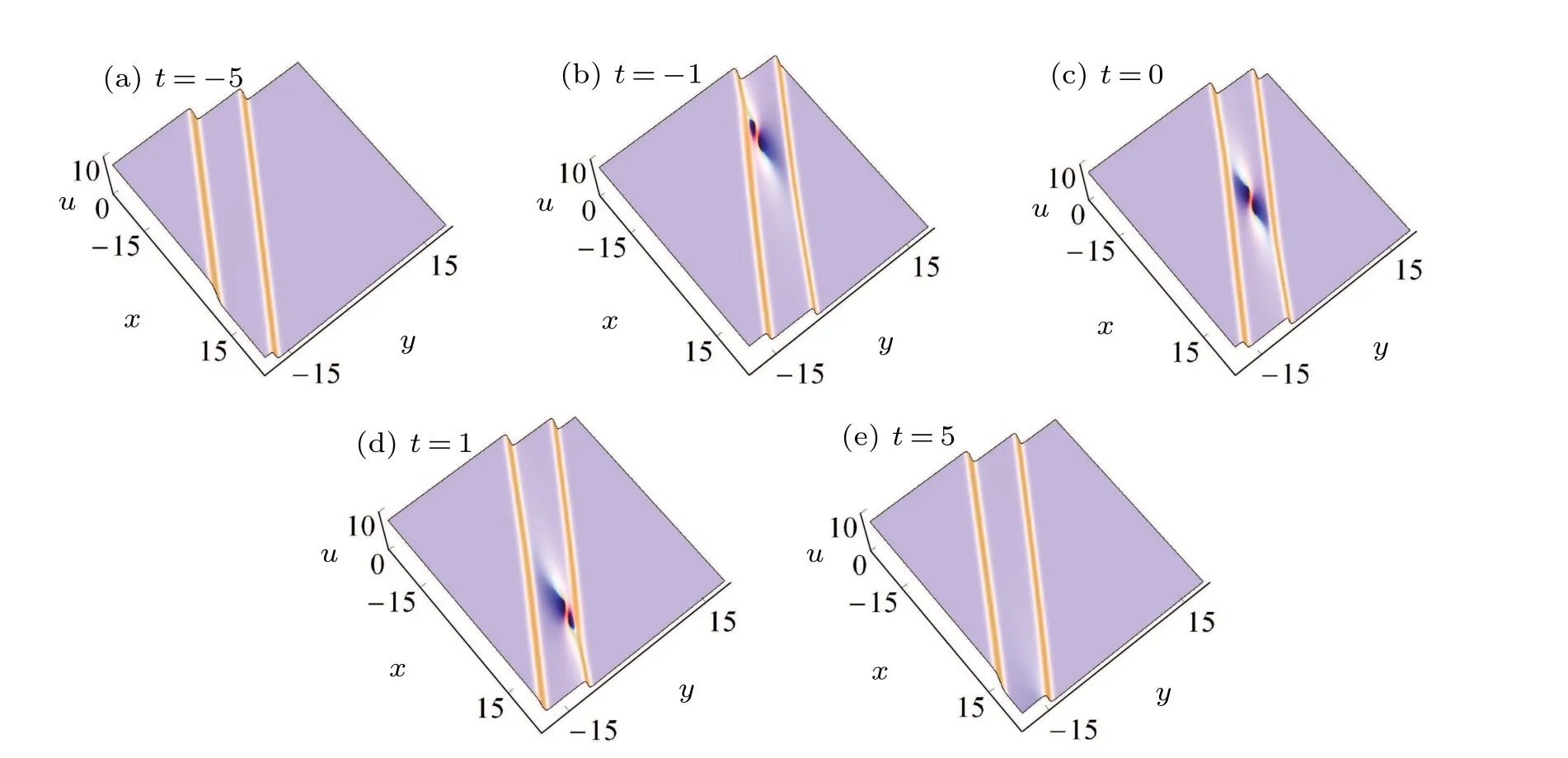
Fig.1. Interaction between a lump and two kink solitons via solutions(9)with z=0,a=1,b=1,ζ10=2π,ζ20=?2π.
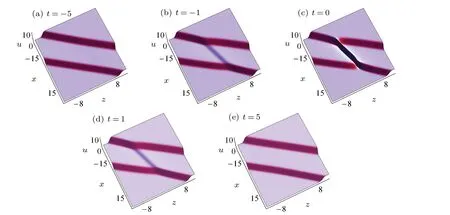
Fig.2. Interaction between a line rogue wave and two kink solitons via solutions(9)with y=0,a=1,b=?1/√3,ζ10=2π,ζ20=?2π.
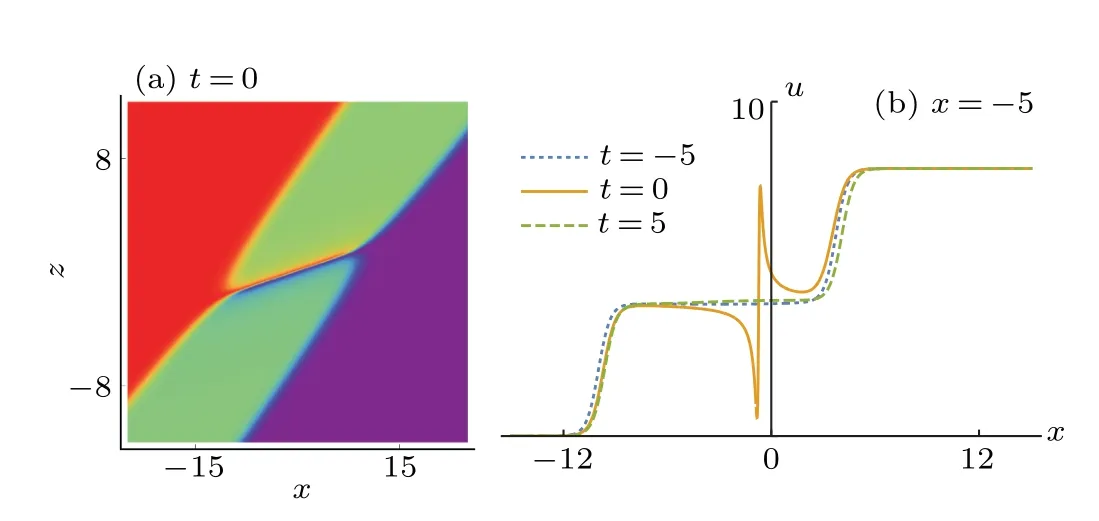
Fig.3.(a)The density plot of interaction at t=0,(b)trajectories at different positions in Fig.2(a). The parameters are the same as those in Fig.2.
3.2. Higher-order lump and rogue wave
WithN=2 in solutions (7), we can derive the secondorder semi-rational solutions of Eq.(1):
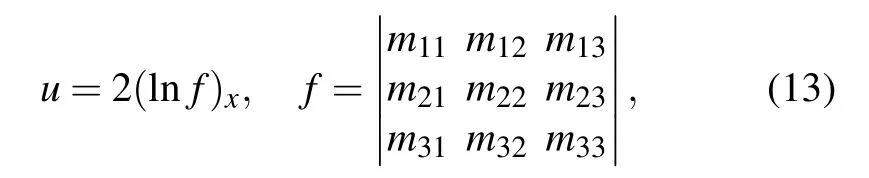
wheremjkare given by solutions(7). The same as the above analyses, those solutions will generate interactions between three solitons and higher-order rational solutions,including(I)between three kink solitons and the line rogue wave on thex–zplane with constrainta2?3b2=0, as shown in Fig. 5;(II)between three kink solitons and two lumps in other cases,as shown in Fig. 4. The three kink solitons are of the same wavenumber(a+ib), thus they are all nearly parallel. In addition to the different kinds of rational solutions,the distance between the two kink solitons will also remarkably affect such wave interactions, which can be adjusted via the phase shifts constantsζj0. Thus,in what follows,we will discuss the interactions between the lumps (line rogue waves) and three kink solitons graphicly.
We present the interactions between two lumps and three kink solitons on thex–yplane as an example. With different choices ofζj0, there are two kinds of interaction. The one is, by settingζ10>ζ20>ζ30, we see that two lumps arise from the leftmost (in thex-axis direction) kink soliton,go through the middle one, and fuse into the rightmost kink soliton,as shown in Figs.4(a)–4(d);The other is,while settingζ10>ζ30>ζ20,as shown in Figs.4(e)–4(h),we see only one lump arises from the leftmost kink soliton,with its shape varying when it goes through the middle kink soliton. And later,it shows a two-lumps outline(which means that there is another lump arising from the middle kink soliton). Subsequently,the two lumps fuse into the rightmost kink soliton.
In the same way, with different choices ofζj0, we will present two interactions between line rogue wave and three kink solitons by settinga2?3b2= 0 on thex–zplane in Fig.5. Withζ10>ζ20>ζ30,it can be seen that one line rogue wave rises up in the segment between the leftmost and rightmost kink solitons, crosses the middle one, and arranges on a line nearly; and soon it reaches higher amplitude att=0,in the meantime, these two segments of the rogue wave connect together; and then the two segments retreat back with amplitudes decreased, and finally disappear. While by settingζ10>ζ30>ζ20,the rogue wave behaves almost the same as the former case except for that one segment of the rogue wave increases its amplitude after retreating back, as shown in Fig.5(g). Thus,the dynamics of these two interactions between the rogue wave and kinks are nearly the same,different from those in Fig.4. Besides,it is noteworthy that the secondorder rational solutions do not generate two-line rogue waves(arranging on two lines) or a second-order rogue wave (with three wave arms). Hence,in this paper,we call such localized line rogue waves as one rogue wave,distinctly different from those reported in Refs.[23,26].
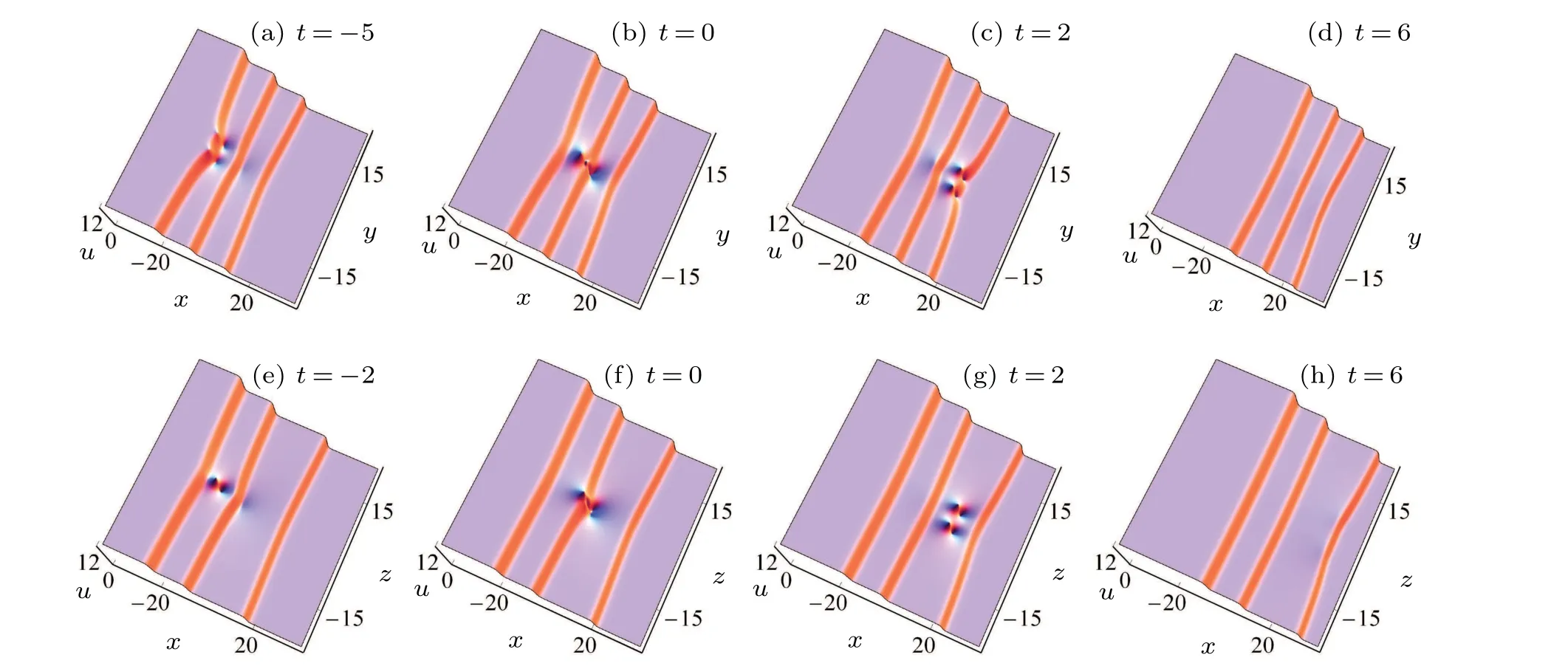
Fig.4. Interactions between two lumps and three kinks via solutions(13)with a=1,b=0. (a)–(d)ζ10=6,ζ20=0. and ζ30=?6;(e)–(h): ζ10=6π,ζ20=?6π,and ζ30=0.
Fig. 5.Interactions between one rogue wave and three kinks via solutions (13) withy=1,a=1,b=?1/√3, and (a)–(d):ζ10=5,ζ20=0 andζ30=?5;(e)–(h):ζ10=4π,ζ20=?4π,andζ30=0.
4. Conclusions
In this paper, we investigated certain rogue waves of the(3+1)-dimensional BKP equation. Via the KP hierarchy reduction, semi-rational solutions in the determinant form of Eq.(1)have been constructed,which generate two novel nonlinear wave behaviors: (i) the interaction between one lump and two kink solitons with the lump developing from one kink soliton and then fusing into the other one; (ii) the interaction between one line rogue wave and two kink solitons on thex–zplane with the line rogue wave growing from and then decaying into the constant background between the segment of the two solitons. We have found that evolutions of the lump and line rogue wave are localized both in time and space, which means that such lump and line rogue wave play as a rogue wave. In addition, we have also discussed the second-order semi-rational solutions graphicly, which describe two types of interactions between two lumps(one line rogue wave)and three kink solitons.
Acknowledgements
Project supported by the Fundamental Research Funds for the Central Universities (Grant Nos. 2021XJLX01 and BLX201927),China Post-doctoral Science Foundation(Grant No. 2019M660491), and the Natural Science Foundation of Hebei Province,China(Grant No.A2021502003).
- Chinese Physics B的其它文章
- Fault-tolerant finite-time dynamical consensus of double-integrator multi-agent systems with partial agents subject to synchronous self-sensing function failure
- Nano Ag-enhanced photoelectric conversion efficiency in all-inorganic,hole-transporting-layer-free CsPbIBr2 perovskite solar cells
- Low-voltage soft robots based on carbon nanotube/polymer electrothermal composites
- Parkinsonian oscillations and their suppression by closed-loop deep brain stimulation based on fuzzy concept
- Temperature dependence of spin pumping in YIG/NiO(x)/W multilayer
- Interface effect on superlattice quality and optical properties of InAs/GaSb type-II superlattices grown by molecular beam epitaxy

