POINTWISE SPACE-TIME BEHAVIOR OF A COMPRESSIBLE NAVIER-STOKES-KORTEWEG SYSTEM IN DIMENSION THREE*

Xiaopan JIANG (姜曉盼) Zhigang WU (吳志剛)

Department of Mathematics,Donghua University,Shanghai 201620,China

E-mail: 1783685777@qq.com;zgwu@dhu.edu.cn

Abstract The Cauchy problem of compressible Navier-Stokes-Korteweg system in R3 is considered here.Due to capillarity effect of material,we obtain the pointwise estimates of the solution in an H4-framework,which is different from the previous results for the compressible Navier-Stokes system in an H6-framework [24,25].Our result mainly relies on two different descriptions of the singularity in the short wave of Green’s function for dealing initial propagation and nonlinear coupling respectively.Our pointwise results demonstrate the generalized Huygens’ principle as the compressible Navier-Stokes system.As a corollary,we have an Lp estimate of the solution with p ＞1,which is a generalization for p ≥2 in [33].

Key words Navier-Stokes-Korteweg system;Green’s function;Large time behavior

1 Introduction

The compressible fluid model of Korteweg type was introduced by Korteweg [20] and deduced rigorously in Dunn and Serrin [9].The model governs the motions of the compressible isothermal viscous capillary fluids and is formulated as

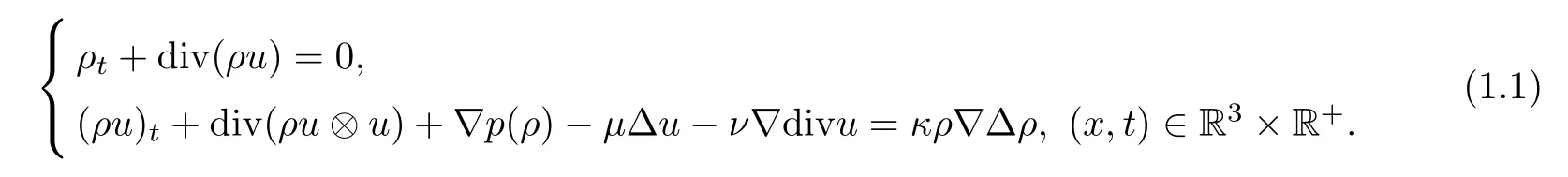
Here the unknownsρ(x,t),u(x,t) are the density and velocity of fluid,respectively.The pressurep=p(ρ) satisfiesp′(ρ)＞0 forρ ＞0.The constantsμ ＞0 andν≥0 are the viscosity coefficients,andκ ＞0 is the capillary coefficient.

There are a lot of mathematical studies on the compressible Navier-Stokes-Korteweg system(1.1),including on the weak solution in [2,11],the existence in Besov spaces in [3],the local existence of strong solutions in [21] and the global existence of strong solutions in [32],the maximalLp-Lqregularity in [28],the global existence of a smooth solution in [12] and theL2-decay rate of the smooth solution in [10,33].With regard to the nonisothermal case,we refer to [15] and [16] for the global existence and the decay rate of the smooth solution with small initial energy,respectively,and [17] for the vanishing capillarity limit.

We were interested in space-time estimates on the wave propagation of the smooth solution.Since the conservative structure of the system on the densityρand momentumm=ρuis needed when dealing the nonlinear convolution estimates,we supplement the system with initial data

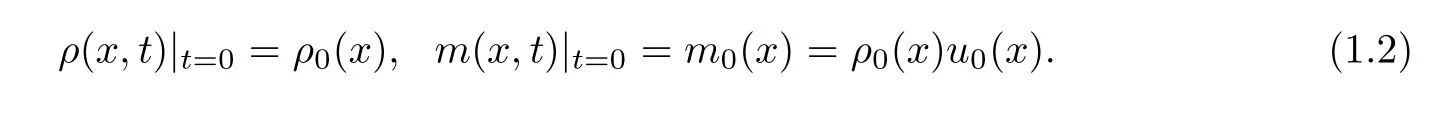
The large time behavior of the compressible Navier-Stokes system is one of the most important topics in studying fluid models;see [7,8,18,19,22,27] and references therein.Nevertheless,L2estimates can only exhibit the dissipative properties of solutions;cannot reveal the behavior on wave propagation.In order to explicitly describe the wave propagation,one needs to consider the space-time pointwise estimates.The pioneering works were Zeng [39] for the isentropic Navier-Stokes system and Liu and Zeng [26] for quasilinear hyperbolic-parabolic systems in dimension one.For three dimensional case,Hoffand Zumbrun [14] and Liu and Wang[25] studied the pointwise estimates of Green’s function and the pointwise estimates of the solution for the nonlinear problem for the isentropic Navier-Stokes system,respectively.Later on,there appeared a series of efforts on these kinds of estimates for other models,including on the Euler system with damping [30,36],refined estimates for the isentropic and non-isentropic Navier-Stokes system [4,5,24],the Navier-Stokes-Poisson system and the Navier-Stoke-Maxwell system [6,31,34,35],thermal non-equilibrium flow and the Boltzmann equation [23,37,38].

The aim in this paper is to investigate the capillarity effect of material and look for the difference betweenκ ＞0 (NSK) andκ=0 (NS) when deducing the pointwise estimates by using Green’s function method.Whenκ=0,the pointwise estimates in [4,24,25] are established in theH6-framework due to the singularity of Green’s function and the quasi-linearity of the system.For NSK here,the Korteweg termκρ?Δρhas the third order derivative;it seems that one needs higher regularity assumption on the initial data to close the ansatz on the pointwise estimates due to the quasi-linearity of NSK.However,we can derive the pointwise results in theH4-framework for NSK.The outline of the proof is as follows:

Step 1We give the representation of the Fourier transform of Green’s function and get the approximate expansions for the eigenvalues in the short wave and the long wave.

Step 2We divide the space-time domain into two parts: inside the finite Mach number region |x| ≤3Mc(1 +t) and outside the finite Mach number regionwith the basic sound speedand some suitably large constantM ＞1.

Step 3When |x| ≤3Mc(1 +t),we give the detailed analysis on the long wave,short wave and the middle part of Green’s function to obtain the pointwise estimates of the Green’s function by using complex analysis.When,we use the weighted energy method to obtain exponential pointwise estimates of Green’s function.

Step 4We deduce the pointwise estimates of the solution for the nonlinear problem through the representation of the solution from Duhamel’s principle.Some convolution estimates on different wave patterns are used to control the initial propagation and nonlinear coupling.

In order to facilitate interpretation,we first state the Fourier transform of Green’s function for the system (1.1) as

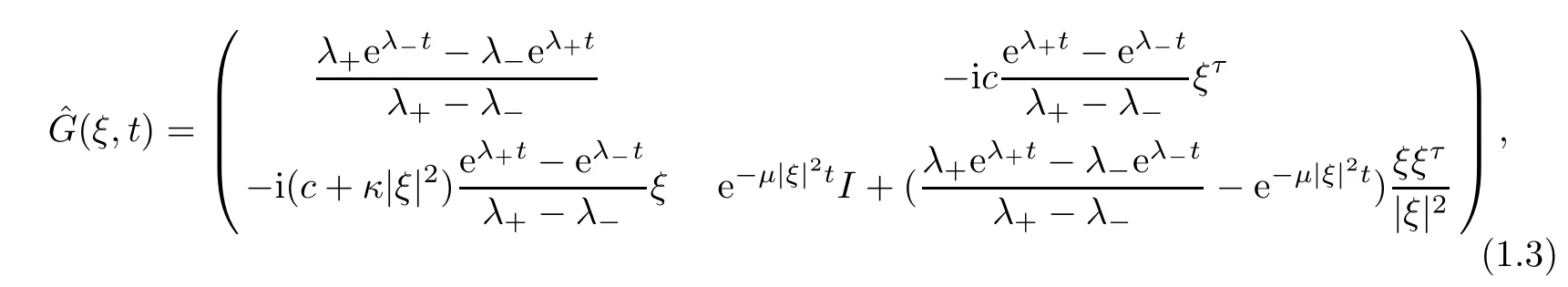
with the eigenvalues

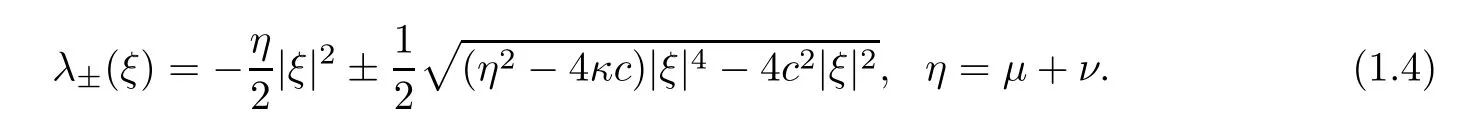
Hereξis the variable in the space of the Fourier transform.As we know,there exist singularities in the short wave for the previous results on NS mentioned above.One of these is from the eigenvalueλ(ξ)～-|ξ|2which is like a heat kernel when |ξ| ?1,and it leads to the short wave behaving in a pointwise sense as(denoted byGS1).Obviously,this is singular whent=0.The other one is from the eigenvalue satisfying -C1≤λ(ξ) ≤-C2with positive constantsC1andC2when |ξ| ?1;this causes the short wave to behave as a Diracδ-function or aδ-like function with an exponential decay rate denoted byGS2.Since NS is quasi-linear,to close the ansatz on the pointwise estimates one needs to use the method of Green’s function together with the energy method.In fact,the pointwise estimates for the solution are based on utilizing the representation of the solution from Duhamel’s principle and Green’s function.Thus,we need to develop the ansatz assumption concerning the pointwise estimates of the lower order derivatives and theL∞-estimates of the higher order derivatives for the solution.For the initial propagation,one has to put all of the derivatives on the initial data due to these two singularities.For the nonlinear interplay,the different singularities ofGS1andGS2in the short wave mean that one has to put all the derivatives on the nonlinear terms when estimating the convolution ofGS2and the nonlinear terms,and one can only put one derivative onGS1when estimating the convolution betweenGS1and the nonlinear terms.

A question that arises is,how can we minimize the requirement on the regularity of the initial data for NSK? First of all,from (1.3)–(1.4),we find that all of the eigenvalues for NSK behave asλ(ξ)～-|ξ|2when |ξ| ?1,which is different from NS.Based on this,we can relax the regularity condition on the initial data by developing two different descriptions on the short wave of NSK.On the one hand,to replace the exponential decay assumption of the initial data on the spacial variablexand its derivatives for NS [4] by the algebraic decay assumption on the spacial variablexfor NSK here,the singular partGS1cannot be used when dealing with the convolution of the short wave and the initial data.In fact,the exponential decay in space of the initial data is used to avoid the singularity ofGS1att=0 when dealing with the convolution of the short wave and the initial data;at this time one needs to separate the space-time domain and use the weight energy estimates.To relax the exponential decay assumption on the initial data,we replace the previous descriptionGS1by a new one,which is similar toGS2.That is,we useδ(x) orDxδ(x) to describeGS1.This will help us to avoid using the exponential decay assumption onx.At the same time,this new description is also used to estimate Green’s function outside a finite Mach number regionto obtain the regular estimate,since this description of singularity for the short wave is regular when |x| ≥1.

On the other hand,we consider the nonlinear coupling.Notice that the convolution on the interplay of the Huygens’ waves in the long wave determines that we require the pointwise ansatz ofdue to the nonlinear term of the capillarity effect when deriving the pointwise estimate of the solution (ρ,m).To minimize the requirement on the regularity,we want to put more derivatives on Green’s function when estimating the nonlinear convolutions due to the quasi-linearity of the system.Hence,in this situation,we use the description of the short wave asGS1such that one can take the integral by parts once,since the nonlinear convolution is on both spatial and temporal variables.With these preparations,we can close the pointwise ansatz in theH4-framework.We believe that using different descriptions for the singularity of the short wave to deal with initial propagation and nonlinear coupling,respectively,could also be applied to the other hyperbolic-parabolic systems.

The following is the main result in this paper:

Theorem 1.1Assume that the initial data (ρ0,m0) satisfying:=ε0are small and the background density＞0.Then there exists a unique,global,classical solution (ρ,m) to the Cauchy problem (1.1)–(1.2).If,furthermore,for 0 ≤k≤2,

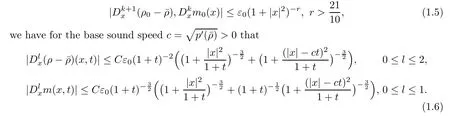
Remark 1.2The estimate (1.6) shows that NSK also exhibits the generalized Huygens’principle as NS.Compared to the previous space-time estimates for NS in theH6-framework in [24,25],we obtain the similar pointwise result for NSK under a relaxed condition: theH4-framework.Here the capillarity effect of material is so crucial that we can freely use these two different descriptions for the short wave as required.

Corollary 1.3(Lpestimates) Under the assumptions in Theorem 1.1,we have the followingLp(R3) estimates of the solution:

Throughout the paper,CandCidenote positive generic constants that may vary at different places.is theαorder derivative of a smooth functionf,and sometimes we also useto denote thek-order derivative offwith |α|=k.We useLpandWm,pto denote the usual Lebesgue and Sobolev spaces on RnandHm=Wm,2,with norms ‖ · ‖Lp,‖ · ‖Wm,p,‖ · ‖Hm,respectively.

The rest of this paper is arranged as follows: in Section 2,we give the pointiwse estimates of Green’s function by the decomposition of the long and short waves together with the decomposition of the space-time domain.In Section 3 we deduce the pointwise estimates of the solution for the nonlinear problem by some convolution estimates.In Appendix,we give some lemmas that are used in Sections 2 and 3.

2 Green’s Function

This section is devoted to giving the pointwise description of Green’s function.

2.1 Preliminaries

In this section,we consider the Cauchy problem for the linearized Navier-Stokes-Korteweg system of the reformulated nonlinear problem:

HereG(x,t) is Green’s function and its Fourier transform is

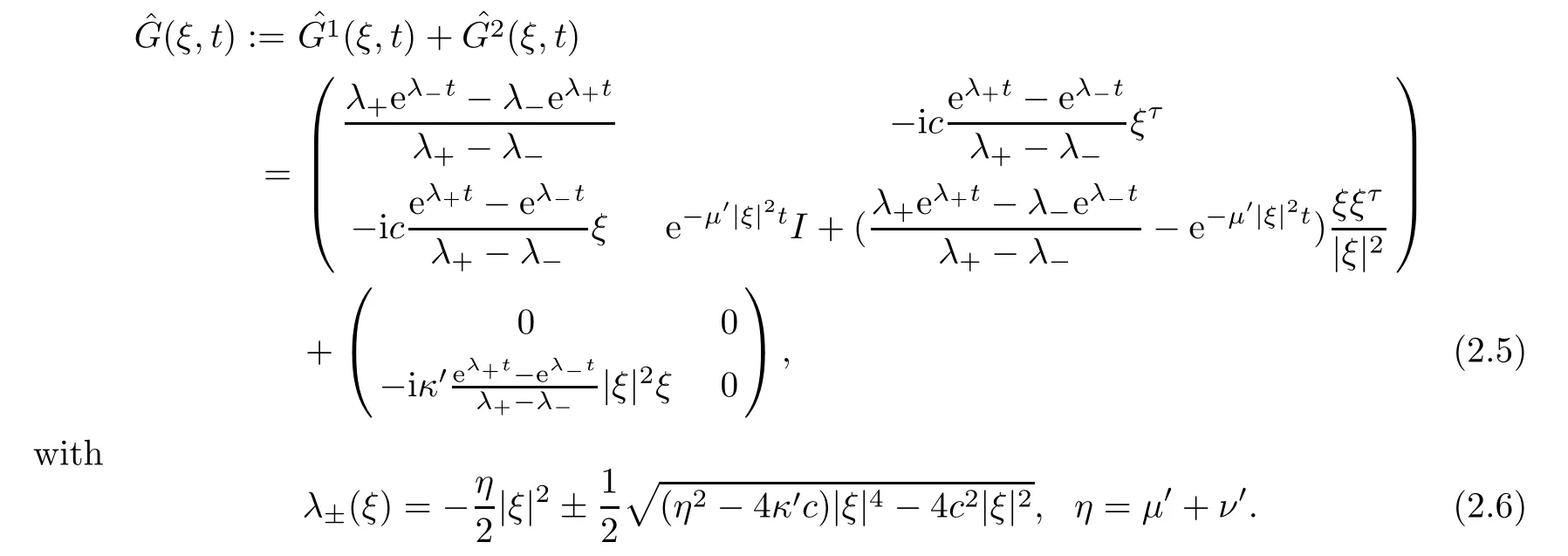
The representation above holds for |ξ|0.

To derive the pointwise estimates of Green’s functionG(x,t),we will use the decomposition of the long wave and short wave forG(x,t) as follows:

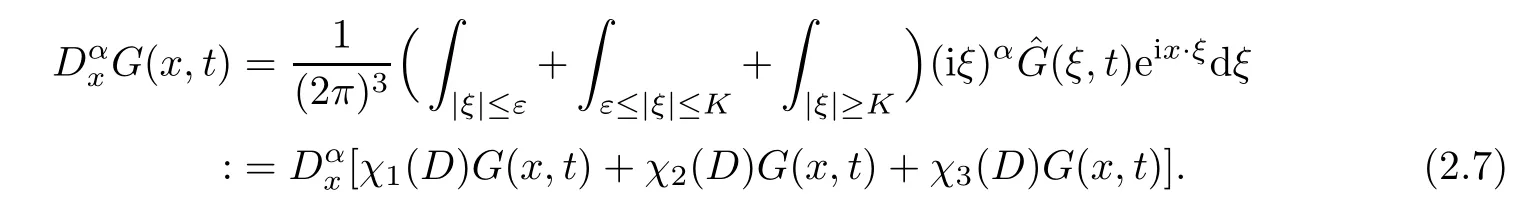
After direct computations,we can get the following estimates for the spectrumsλ±(ξ):

Lemma 2.1Whenη2-4κ′c=0 and |ξ| ?1,it holds that

Whenη2-4κ′c0 and |ξ| ?1,it holds that

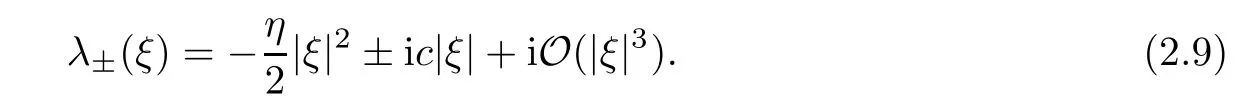
Whenη2-4κ′c ＞0 and |ξ| ?1,it holds that

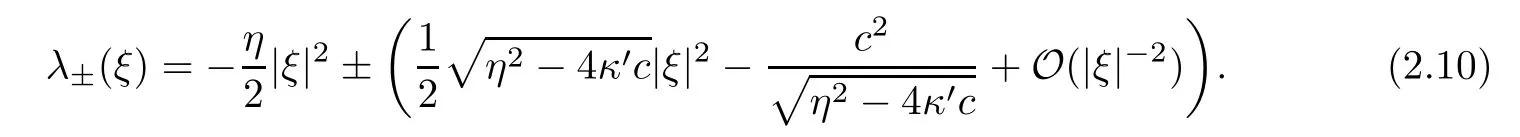
Whenη2-4κ′c ＜0 and |ξ| ?1,it holds that

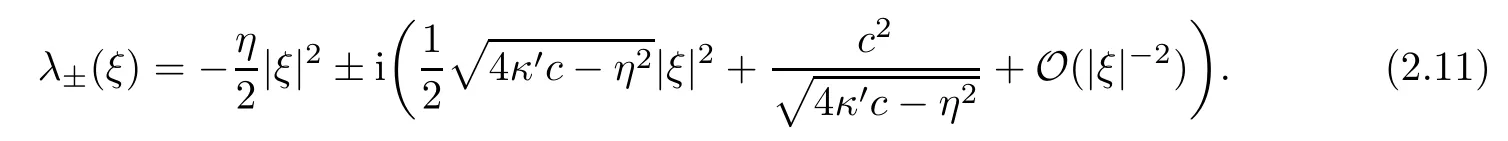
Note that for all of the cases above,the spectrums are analytic when |ξ| ?1,otherwise the complex variable technique cannot be applied.

2.2 Pointwise estimate of Green’s function

In this section,we shall derive pointwise estimates of Green’s functionG(x,t),to this end,we first study its Fourier transform ?G(ξ,t) by the decomposition of the long and short wave.Additionally,since there exists Riesz transform and the Huygens’ wave in Green’s function,to analyse it clearly,we also decompose the temporal and spatial region inside the finite Mach number region |x| ≤3Mc(1 +t),and outside the finite Mach number region |x| ≥Mc(1 +t),whereM ＞1 is a suitably large positive constant to be determined later.

2.2.1 Inside the finite Mach number region |x| ≤3Mc(1 + t)

First,we consider the long wave,that is,|ξ| ?1.After direct computations,we get

whereβis an analytic function in |ξ|2andβ(0)=0.

To overcome the singularity of the Riesz operator inin (2.15) when |ξ| ?1,we should rewriteas follows:

The estimate for the inverse Fourier transforms ofI1,I2,I3can be deduced as Lemma 4.5 in [5],through complex analysis for the long wave inside the finite Mach number region,which shows that they behave as the heat kernel:

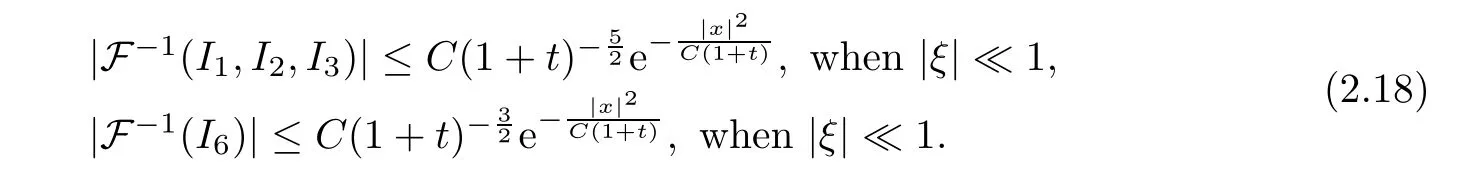
Here the additional decay rate forI1,I2,I3is from the factorξξτcompared with that ofI6.Then,by using Lemma A.1,we have that

For the Riesz waveI4,one can also deduce the following estimate from Lemma 4.7 in [5]:

Finally,the Riesz waveI5can be estimated with the following process:

In summary,we have the pointwise estimate for the long wave ofG22(x,t):

The other terms ofχ1(D)G(x,t) can be treated similarly.For simplicity,we just state these estimates in a conclusion.

Lemma 2.2For any |α| ≥0,the estimates of the long waveχ1(D)G(x,t) inside the finite Mach number region |x| ≤3Mc(1 +t) are

We find that the estimates forχ1(D)G11(x,t) andχ1(D)G12(x,t) only contain the Huygens’wave.This is the basis on which one can obtain that the pointwise estimate of the density is better than that of the momentum;see (1.6).

Next,we study the short wave,which contains the singularity from the initial singularityδ(x) att=0.The capillarity effect causes all of the eigenvalues for the short wave of the Navier-Stokes-Korteweg system to behave asλ±(ξ)=-θ|ξ|2with some constantθ ＞0.This is the biggest difference in the short waves between the Navier-Stokes equations and the Navier-Stokes-Korteweg system.In particular,from Lemma 2.1 and the representation of ?G(ξ,t),we can conclude that

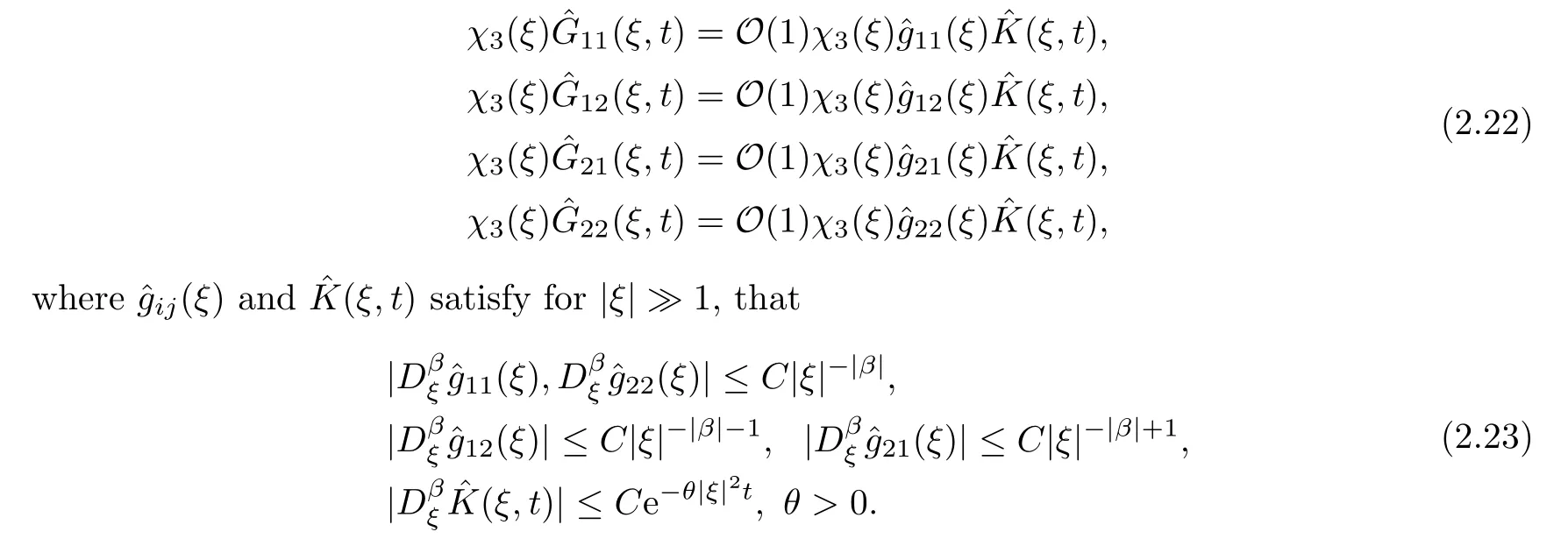
To minimize the regularity condition on the initial data,we need the ensuing lemmas to describe the short wave.

whereδ(x) is the Dirac function.Furthermore,for any |α| ≥0 and any positive integerN,,‖f2‖L1≤C,suppf2(x) ?{x: |x|＜2η0},withη0being sufficiently small.

On the other hand,by the Hausdorf-Young inequality and a similar procedure of the proof in Proposition 4.3 in [14],we have

Lemma 2.4Suppose that(ξ,t)=χ3(ξ)(ξ)e-θ|ξ|2t(θ ＞0) is smooth onξand satisfies

Then,for any |α| ≥0 and any positive constantN ＞0,it holds that

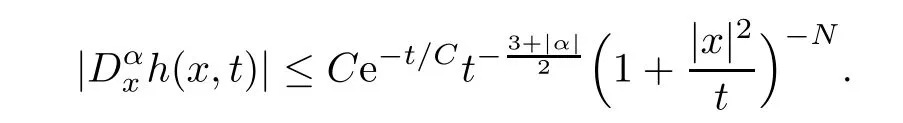
Combining these two lemmas and (2.22)–(2.23),we have the pointwise estimates for the short wave of Green’s functionχ3(D)G(x,t).

Lemma 2.5a) The short wave of Green’s functionχ3(D)G(x,t) satisfies

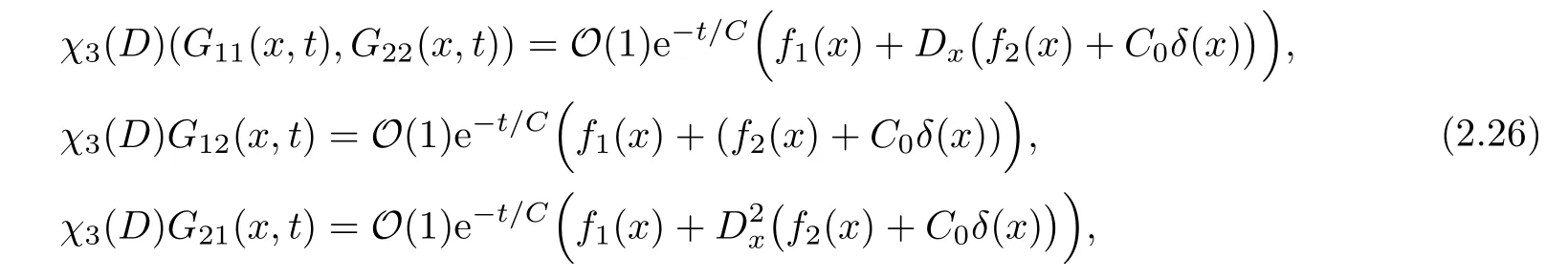
whereδ(x) is the Dirac function.Furthermore,for any |α| ≥0 and any integerN ＞0,we have that

withη0being sufficiently small.

b) For any |α| ≥0 and any integerN ＞0,the short waveχ3(D)G(x,t) also satisfies

Remark 2.6The first estimate (2.26) implies that the singularity is only atx=0,which can help us to derive the regular estimates outside the finite Mach number region |x| ≥Mc(1 +t).Additionally,we also use (2.26) to estimate the initial propagation in the last section.On the other hand,we use the second estimate (2.27) to deal with the nonlinear interplay,since at this time one can put a derivative on the short wave when dealing with the convolution of the short wave and the nonlinear terms,such that one can reduce the requirement of the regularity of the initial data.

Finally,the procedure for estimating the middle part of Green’s function is standard,since the difficulties from |ξ| ?1 and |ξ| ?1 do not exist any longer;see [5,24].For simplicity,we give the following estimate without proof:

Lemma 2.7For any |α| ≥0,the estimate of the middle partχ2(D)G(x,t) inside the finite Mach number region |x| ≤3Mc(1 +t) is

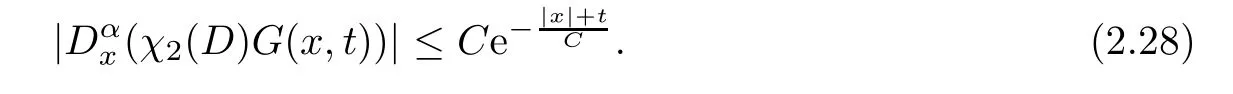
In summary,Lemma 2.2,Lemma 2.5 and Lemma 2.7 yield the pointwise estimate for Green’s function inside the finite Mach number region.

Proposition 2.8For any |α| ≥0,Green’s functionG(x,t) in the finite Mach number region |x| ≤3Mc(1 +t) satisfies

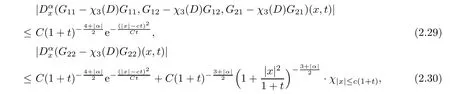
whereχ3(D)Gij(x,t) satisfies the estimate in Lemma 2.5.

2.2.2 Outside the finite Mach number region|x| ≥Mc(1 +t)

We should use the estimate of Green’s function inside the finite Mach number region to give the estimate outside the finite Mach number region as in [29].To this end,we consider the homogeneous initial condition and non-homogeneous boundary value problem:

We are going to use the weighted energy method to derive the estimate of the problem (2.31).Thus,we introduce the weight functionw(x,t)=eδ(|x|-Lt)with a small positive constantδand a large positive constantL,which will be determined later.It is easy to see,and,?tw=-δLw.Then we have the following:

Lemma 2.9For,there exists a constantC ＞0 independent of |x| andtsuch that Green’s function satisfies,for any |α| ≥0,

Here the boundary terms are from the Divergence theorem and the Co-area formula.We denote all the boundary terms byI2,for convenience.

I1can be estimated as follows by using integration by parts and the Schwarz inequality:

Then,by choosing a suitably large constantL ＞0 and a suitably small constantδ ＞0,and noticing,we know that there exists a constantC1＞0 such that

ForI2,we need the information of the variables (ρ,m) and their derivatives on the boundary?Dtfrom Proposition 2.8.Notice that the second term in (2.30) disappears when |x|＞c(1+t).Hence,we know that there exists a constantC2＞0 such that

where we have also used the assumption,which excludes the singularity at|x|=0 in (2.26) in Lemma 2.5.Then,(2.34),together with the smallness ofδin the weight functionw(x,t),suffices to imply that

From (2.33) and (2.35),we can obtain,by using the Grnwall’s inequality,

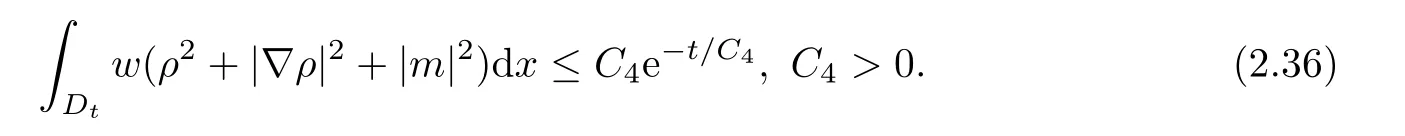
Next,in order to apply the Sobolev inequality to obtain the pointwise estimate,we need the higher order derivative of the solution (ρ,m) for (2.31).The process is similar to that above,we omit it for simplicity.Finally,we have the following estimate for any positive integerl:

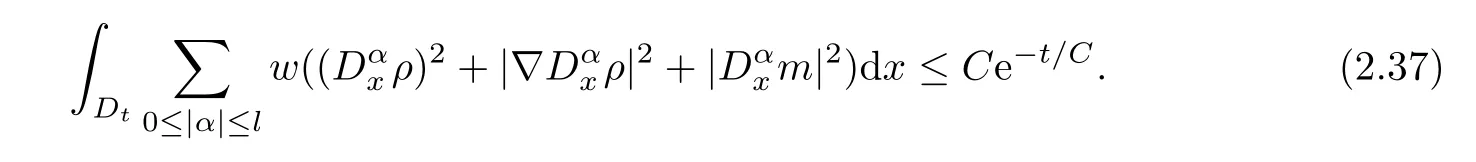
Then,by using the Sobolev embedding theorem,we immediately get that

By using the smallness ofδagain,we can immediately get (2.32). □

In conclusion,we obtain the following pointwise estimates forG(x,t):

Proposition 2.10For any |α| ≥0,Green’s functionG(x,t) satisfies

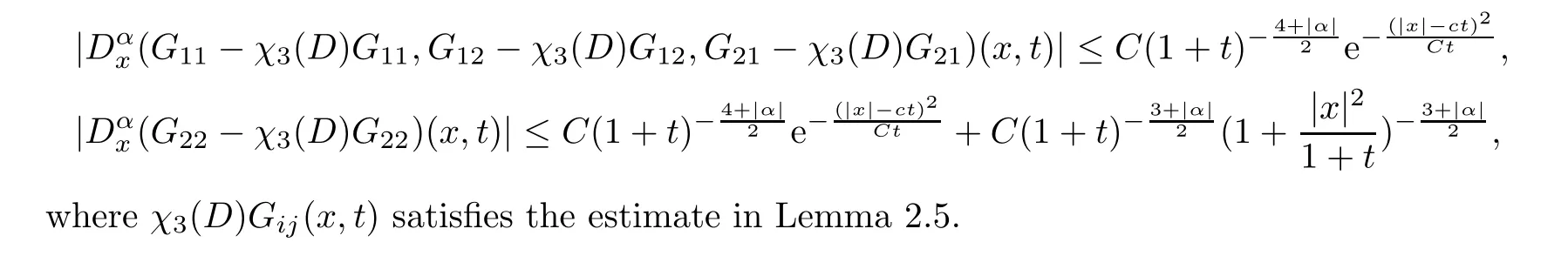
3 Pointwise Estimates of the Nonlinear System

Since there exists a Huygens’ wave in Green’s function,to derive the pointwise estimates for the nonlinear system,we have to use the conservative structure of the nonlinear system,due to the convolution estimates in the Appendix.To this end,we rewrite the capillary term

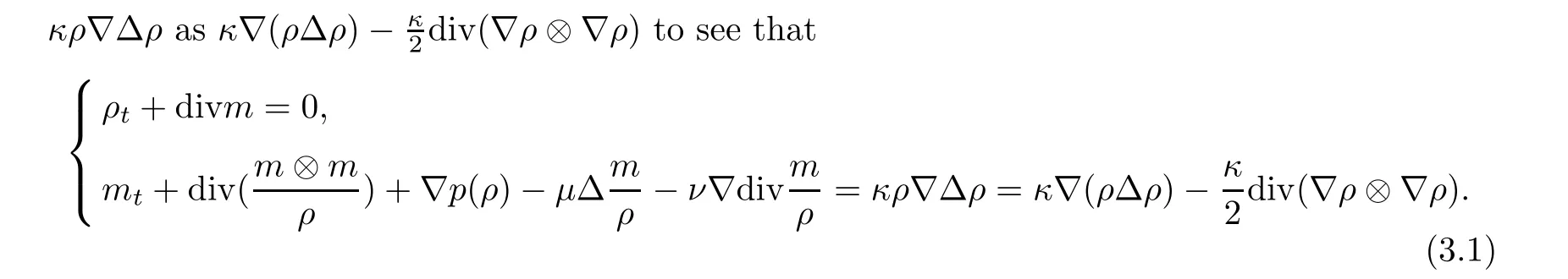
The linearized system is given by

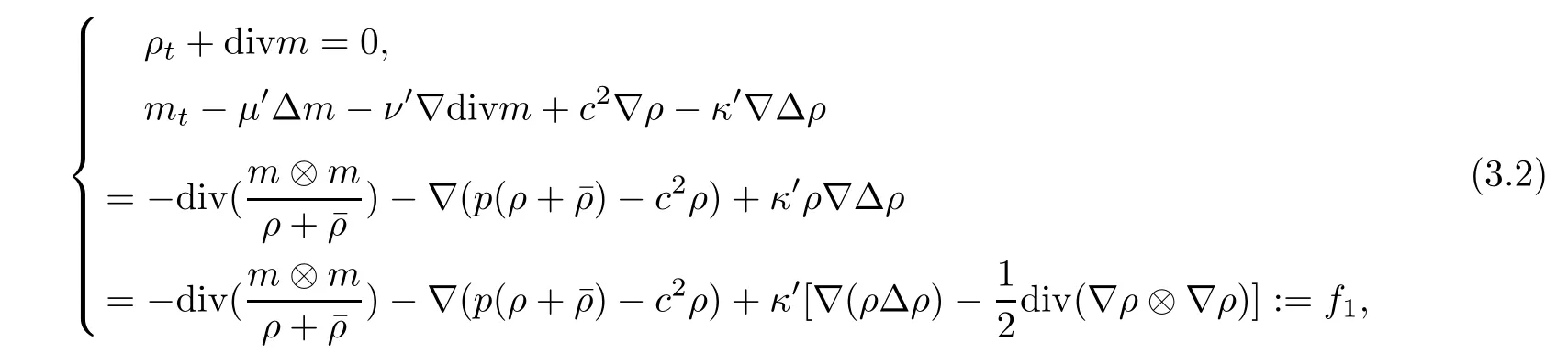
whereμ′,ν′,κ′are defined as in Section 2.1.

Then,we give the representation of the solution (ρ,m) of (3.2) by Duhamel’s principle as follows:

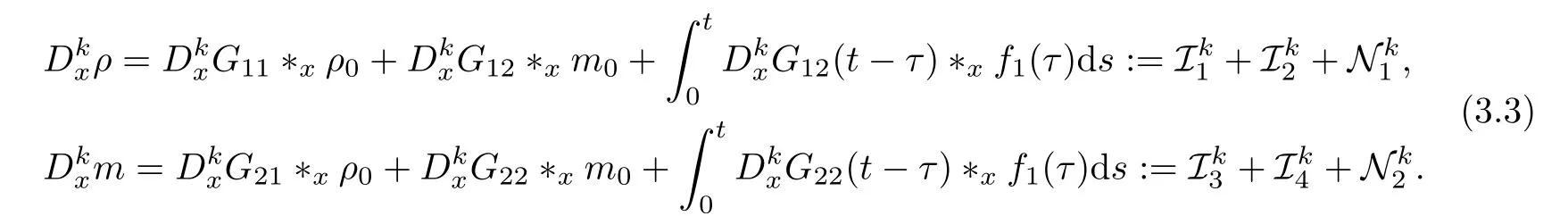
3.1 Initial propagation

We first study the propagation of the initial data.The assumption on the initial data is

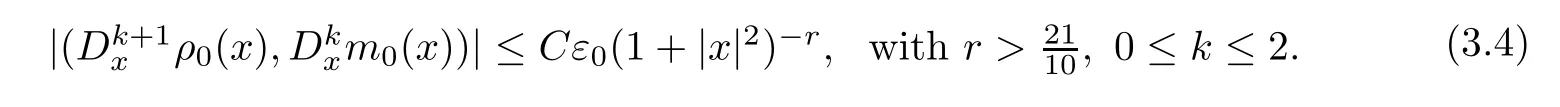
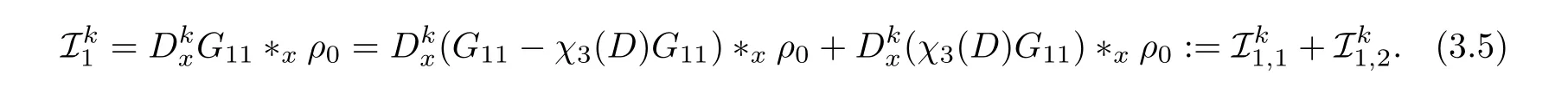
By Proposition 2.10,the Assumption (3.4) and Lemma A.3,we immediately get that

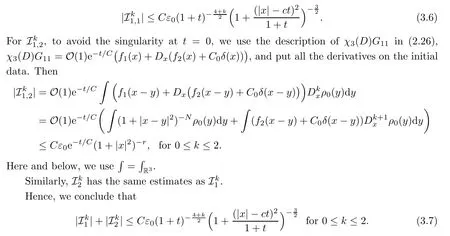
In the same way,we can get,for 0 ≤k≤1,that

Here the second term on the right hand side of (3.8) is from the convolution of the Riesz wave in the long wave ofG22and the initial data.

3.2 Nonlinear coupling

First of all,it is easy to see the nonlinear term

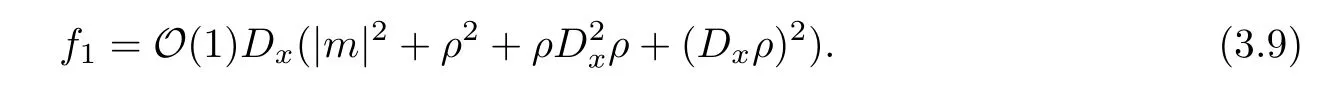
To derive the pointwise estimates for the solution of the nonlinear system,we shall give the following ansatz for 0 ≤k1≤2 and 0 ≤k2≤1:

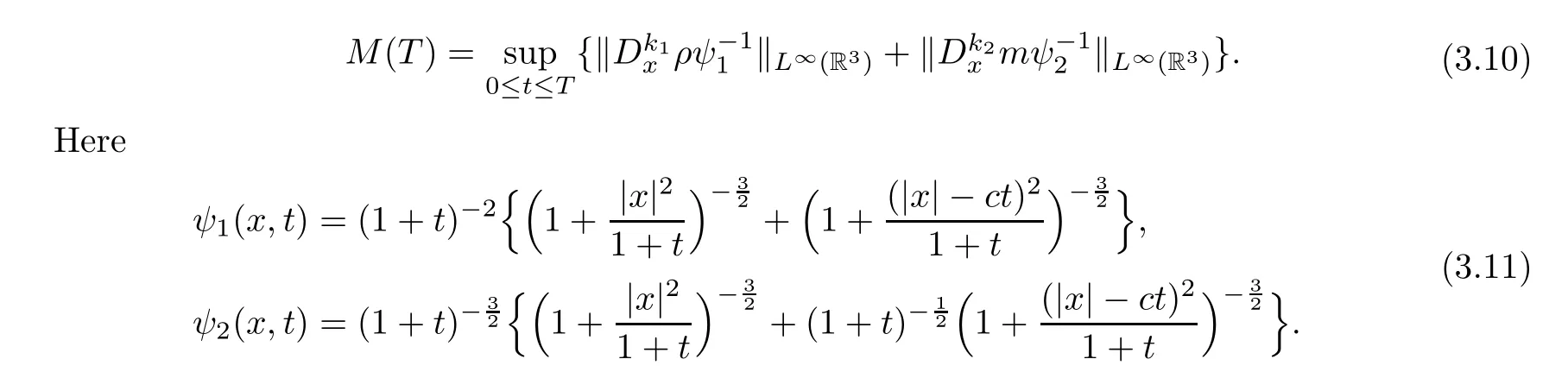
In what follows,we mainly prove thatM(T) ≤C.Since the Navier-Stokes-Korteweg system is quasi-linear,one needs the a priori estimates of the higher derivatives of the solutions in [33]for the closure of the nonlinearity.

We only consider the nonlinear couplingfor the momentumm,since N1can be treated similarly.In fact,

Because there is no singularity inGHandGR,we can put all the derivatives ontoGHandGRwhen estimatingIn these cases,the estimates fork=1 are just the same as the case fork=0.We focus on the convolution containing the nonlinear term

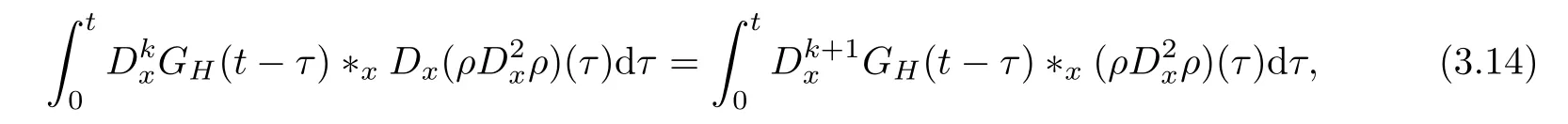
since this nonlinear term has the highest order of the derivative of the unknown variableρ.In particular,this term determines the highest order of the derivative ofρin the ansatz (3.10).In fact,based on the convolution estimates for the coupling of these wave patterns in Lemma A.4,we know that we need the pointwise estimates forto get the pointwise estimate for (ρ,m).This is the reason that we give the ansatz (3.10) in the pointwise sense where the order of the derivatives of the densityρis from 0 to 2.The second term N22can be estimated similarly.

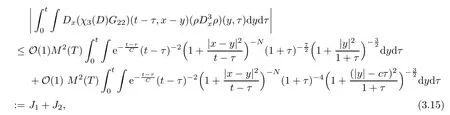
where we have used the fact thatwhich is based on theL2-decay rate of the solution and its derivatives in [10,33] and the Sobolev inequality.This determines that we need the regularity assumption of the initial data to be in theH5×H4-framework.Note that the convolutions in (3.15) are not included in Lemma 4.4 given in the Appendix,however,we can estimate them in the same way as in [24].In fact,for the long time 0＜t0≤τ ＜twith suitablet0,J1andJ2have been estimated in [24] even for the case without the factorFor the short time 0 ≤τ ＜t0＜t,the authors of [24] obtained that

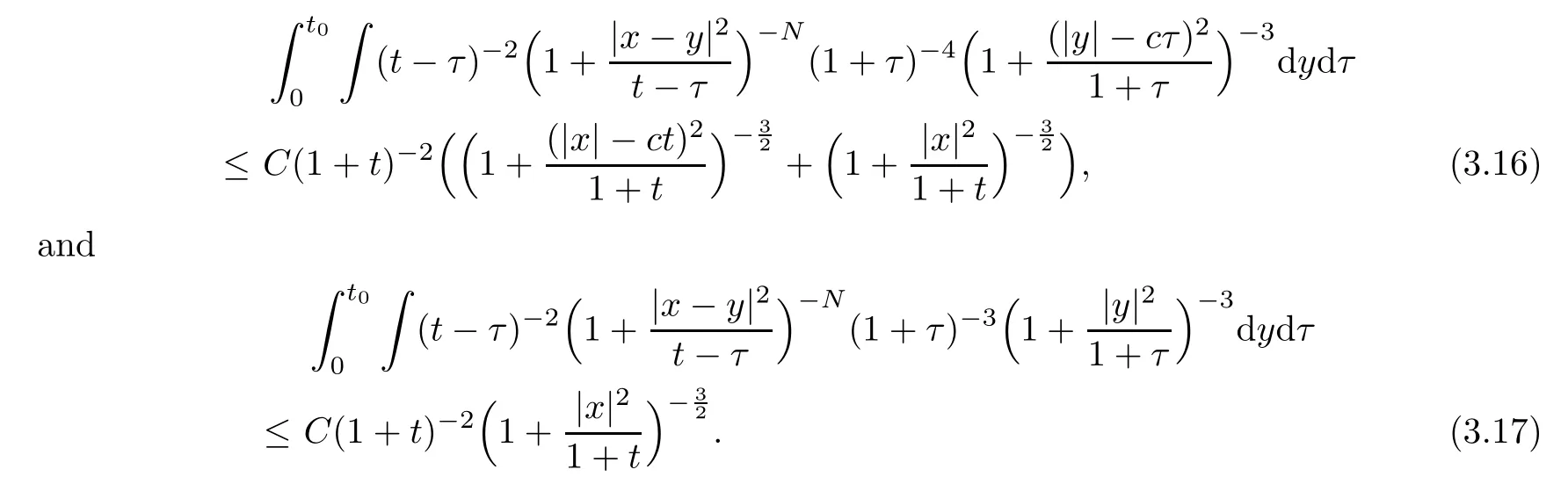
Obviously,the nonlinear terms inJ1andJ2have worse pointwise information on the spacial variablexthan those in (3.16) and (3.17).However,forJ1andJ2in the short time,the additional factorwill provide the exponential decay rate.Hence,one can also get the same pointwise estimates forJ1andJ2as in (3.16) and (3.17).The proof is tedious but direct,we omit the details.

Then,combining the above estimates forwithi=1,2,3,we have

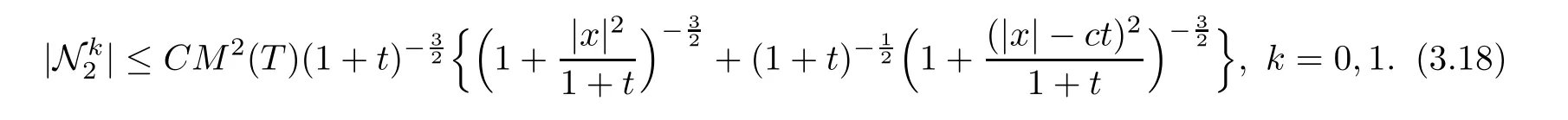
This together with the initial propagation (3.8) forand the representation (3.3),yields that

Simultaneously,noticing the better estimates for both the long wave and the short wave ofG11(x,t) andG12(x,t) compared with those ofG21(x,t) andG22(x,t) in Section 2,it also holds that

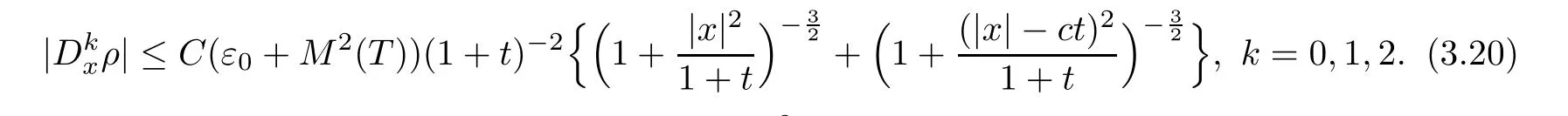
These two estimates give thatM(T) ≤C(ε0+M2(T)) with a positive constantCindependent ofT,which together with the smallness ofε0and the continuity ofM(T),implies thatM(T) ≤C.Thus,we have closed the ansatz (3.10) and completed the proof of Theorem 1.1.

Appendix: Some Useful Estimates

The first lemma is used to derive the Huygens’ wave for the long waves of NS and NSK.

Lemma A.1(see [5]) Letw(x,t) be the wave operator such that its inverse Fourier transformation is.Then one has

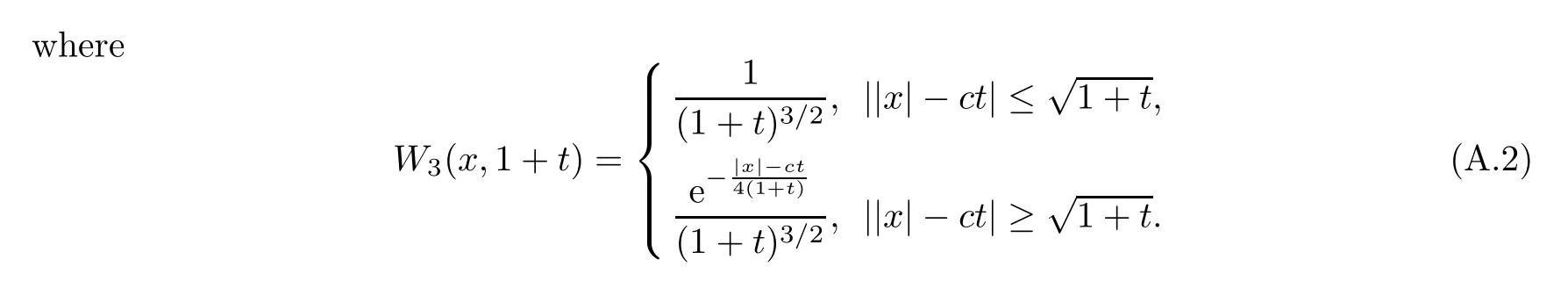
We also need the following lemma when describing the singular part of the short wave:

Lemma A.2(see [30]) If supp(ξ) ?OK=: {ξ,|ξ| ≥K ＞0},and(ξ) satisfies

then there exist distributionsf1(x) andf2(x) and a constantC0such that

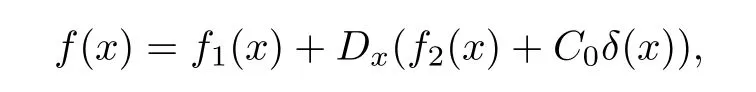
whereδ(x) is the Dirac function.Furthermore,for any |α| ≥0 and any positive integerN,we have that

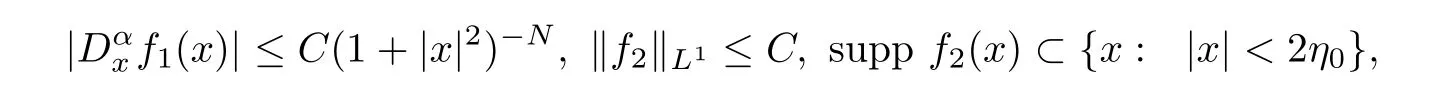
withη0being sufficiently small.

The next two lemmas are used to deal with initial propagation and nonlinear coupling,respectively.

Lemma A.3(see [34]) There exists a constantC ＞0 such that

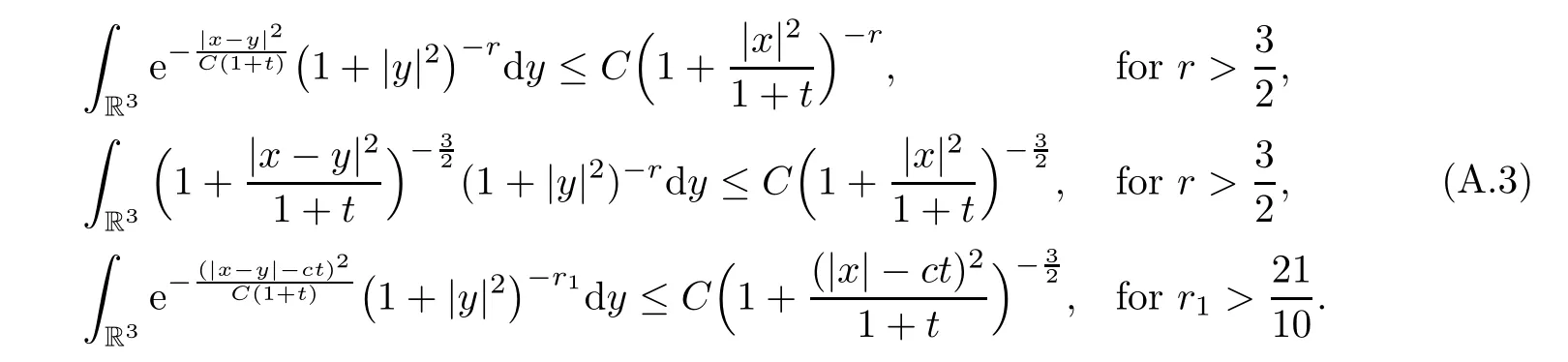
Lemma A.4(see [24]) There exists a constantC ＞0 such that