Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient
WANG Fenling(王芬玲) ,SHI Yanhua(史艷華) SHI Zhengguang(史爭光) ,ZHAO Yanmin(趙艷敏)
(1.School of Science,Xuchang University,Xuchang 461000,China;2.School of Economic Mathematics,Southwestern University of Finance and Economics,Chengdu 611130,China)
Abstract:By using finite element method in spatial direction and classical L1 approximation in temporal direction,a fully-discrete scheme is established for a class of two-dimensional multi-term time fractional diffusion equations with variable coefficient under anisotropic meshes.The stability properties of the approximate scheme are rigorously proved in L2-norm and H1-norm.With the help of high accuracy result between the projection operator and the interpolation operator of the linear triangular finite element,the superclose result with order O(h2+τ2-α)in H1-norm is deduced,where h and τ are the step sizes in space and time,respectively.Then the global superconvergence is presented by means of interpolation postprocessing technique,which is not deduced by the interpolation and projection alone.Finally,several numerical results are implemented to evaluate the efficiency of the theoretical results.
Key words:Multi-term time-fractional diffusion equation;Linear triangular finite element;Anisotropic mesh;Stability;Superconvergence
1.Introduction
During recent years an interest in fractional partial differential equations(FPDEs) has flourished greatly for they can be widely used to modelling anomalous phenomena[1]and many processes,such as the surface water waves can be described by a time fractional Boussinesq equation[2],porous media percolation can be modelled by a FPDE equation based on the experimental data,the non-Markovian evolution of a free particle in quantum physics can be solved by nonlinear time fractional Schr¨odinger equations[3],and so on.Many researchers paid attention to design many efficient numerical algorithms and a variety of numerical methods for the FPDEs have been proposed.For example,for single time-fractional partial differential equations,ZHUANG et al.[4]considered finite difference method,Bhrawy et al.[5]investigated spectral methods,DAI et al.[6]proposed discontinuous Galerkin method methods,LIU et al.[7]presented finite element methods (FEMs),and so on.Moreover,some underlying processes can be more accurately and flexibly modeled by multi-term FPDEs,such as a multi-term model for viscoelastic damping,a two-term equation for distinguishing different states in solute transport[8].
In this paper,by using the spatial finite element method and classicalL1 approximation,we mainly study a fully-discrete approximation scheme for the following two-dimensional multi-term time fractional diffusion equation with variable coefficient:

whereΓ(·) denotes the Gamma function.
With regard to multi-term time FPDEs,there are some fully-discrete approximation scheme based on finite difference methods,spectral methods and FEMs and so on.For example,Soori et al.[9]proposed a sixth-order non-uniform combined compact difference scheme for diffusion-wave equation in one and two-dimensional on non-uniform grids.ZENG et al.[10]established a fully-discrete scheme by a new modified weighted shifted Gr¨unwald-Letnikov formula and proved the linear stability and second-order convergence for both smooth and non-smooth solutions.QIN et al.[11]proposed an effective predictor-corrector method to solve the Bloch equations.Some computationally effective finite difference methods were presented for simulating wave-diffusion equations in [12].Numerical approximations for diffusion equations were established for diffusion equations by means of spectral method in [13].Based on FEM in spatial direction and Diethelm fractional backward difference method in the temporal direction,ZHAO et al.[14]discussed the stability and convergence of a fully-discrete scheme for a one-dimensional multi-term time FPDE.In[15],a space finite element semi-discrete scheme were proposed for (1.1) and nearly optimal error estimates were provided for both cases of smooth and nonsmooth initial data and inhomogeneous term and further a stable fully discrete scheme was developed.REN et al.[16-17]researched on finite difference methods for oneand two-dimensional sub-diffusion equations and diffusion-wave equations,respectively.With the help of bilinear finite element in spatial direction and classical L1 approximation in temporal direction,ZHAO et al.[18]proposed a fully-discrete scheme for diffusion equations and obtained the global superconvergence result.SHI et al.[19-20]proposed an H1-Galerkin mixed finite element method and nonconforming quasi-Wilson finite element method for diffusion equations,respectively,and gave some high accuracy analysis.
Motivated by high accuracy analysis technique by FEM[21],a fully-discrete scheme for(1.1)is proposed by anisotropic linear triangular finite element and classicalL1 approximation.We have settled the efficient numerical methods for the single term time-fractional diffusion equations with variable coefficient in [22].However,as we know,the global superconvergence results for multi-term time-fractional diffusion equations with variable coefficient are still limited.Firstly,some necessary lemmas are shown for stability analysis and error estimates.Then,the stability is proved unconditionally inL2-norm andH1-norm.Based on the property of linear triangular finite element and the high accuracy analysis between the projection operator and the interpolation operator of the element,the supercloseness is deduced.And by interpolating processing technique,the global superconvergence result is also obtained.Moreover,some numerical results are given to test the efficiency of the theoretical results.
The remainder of the paper is organized as follows.In Section 2,by applying the linear rectangular FEM andL1 approximation,a fully-discrete scheme is proposed for (1.1).Some lemmas which are necessary for the unconditional stability analysis are disccussed in Section 3.The unconditional stability analysis is given in Section 4.Moreover,the corresponding convergence results,the supercloseness and superconvergence are deduced.In Section 5,several numerical results are shown to test the efficiency of the theoretical results.In Section 6,some conclusions are drawn.
Throuhout this paper,handτdenote the mesh size and the time step,respectively.Cdenotes a general positive constant which does not depend onhandτandCmay represent different values in different places.
2.Fully-discrete Approximation

Throughout this paper,(·,·) stands for the inner product defined on the spaceL2(Ω) with theL2norm‖·‖0.
Let 0=t0<t1<··· <tN=Tbe a given partition of the time interval,then we have the time stepτ=T/Nandtn=nτ(n=0,1,···,N).For a smooth functionφ(t) on [0,T],we denote

3.Some Lemmas
In this section,we show some necessary lemmas for stability analysis and error estimates.LetIhbe the associated interpolation operator over.
Lemma 3.1[23]Letu∈H2(Ω),under anisotropic meshes,there holds


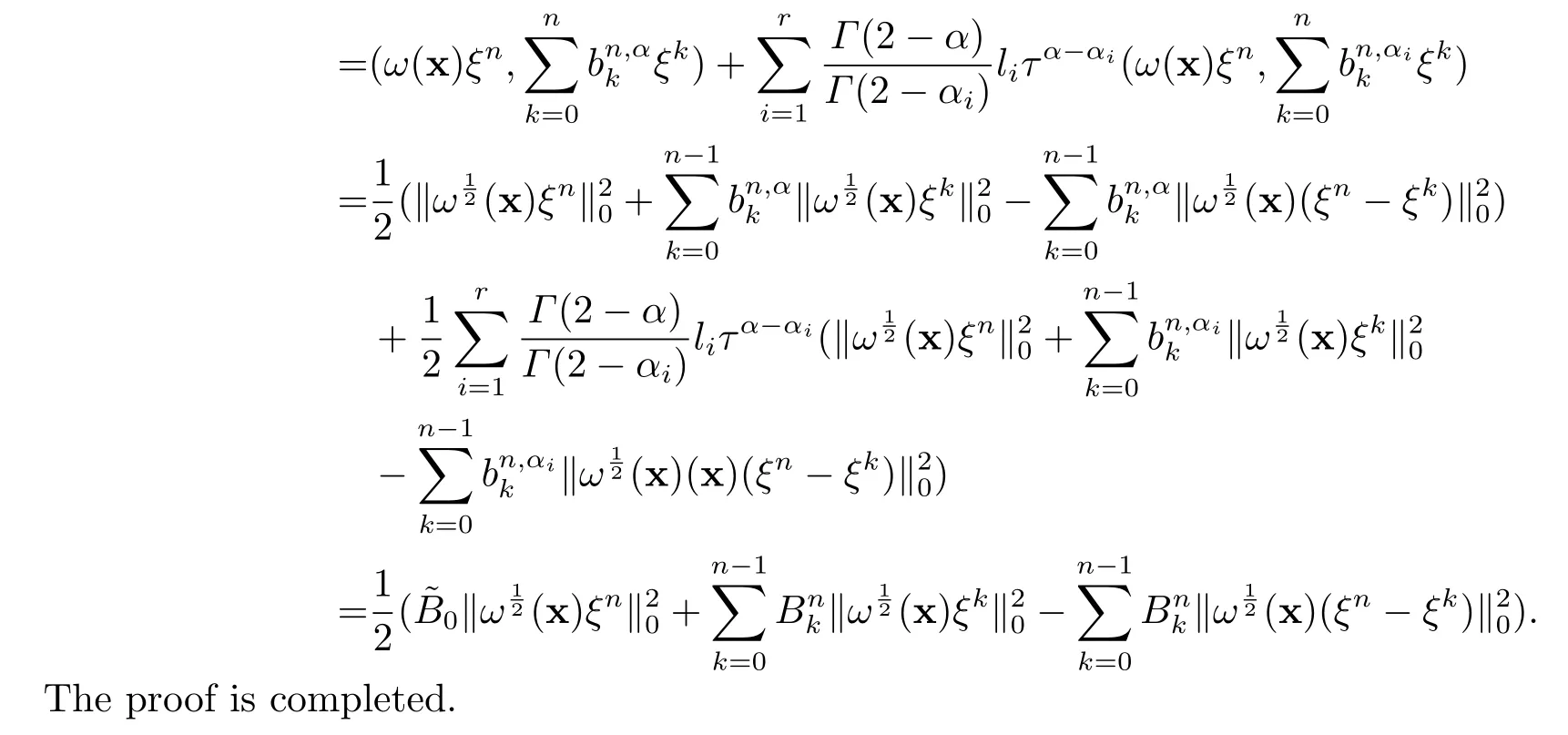
4.Stability Results
In this section,we firstly give the analysis of stability.Theorem 4.1 below shows that the fully-discrete scheme (2.5) is unconditionally stable.
Theorem 4.1Let{Un}be the solution of (2.5),then



5.Superclose and Superconvengence Analysis
By use of error equations,we will present some superclose results and convergence analysis of the finite element fully-discrete approximation scheme in Theorem 5.1 as below.
Theorem 5.1Assume thatun,Unbe solutions of(2.1)and(2.5)att=tn,respectively.Ifu,ut∈H2(ω),utt∈L2(ω),we get



6.Numerical Results
In this section,some numerical results are presented which demonstrate the effectiveness and correctness of the theoretical analysis.
ExampleThe following problem has exact solutionu(x,t)=t3sin πxsin πy.

In order to show convergence results‖un-Un‖0,‖un-Un‖1,superclose results‖Ihun-Un‖1and superconvergence resultsat different times with different orders of Caputo derivatives in spatial direction,we list the corresponding errors and convergence rates in Tables 6.3-6.10 by choosingτ=0.001.The errors and convergence or superconvergence rates are presented attn=0.2,0.4,0.6,0.8 by choosingα=0.4,β=0.2 in Tables 6.3,6.5,6.7 and 6.9,and attn=0.3,0.5,0.9,1 by choosingα=0.7,β=0.4 in Tables 6.4,6.6,6.8 and 6.10,respectively.The results are in line with the theoretical analysis.
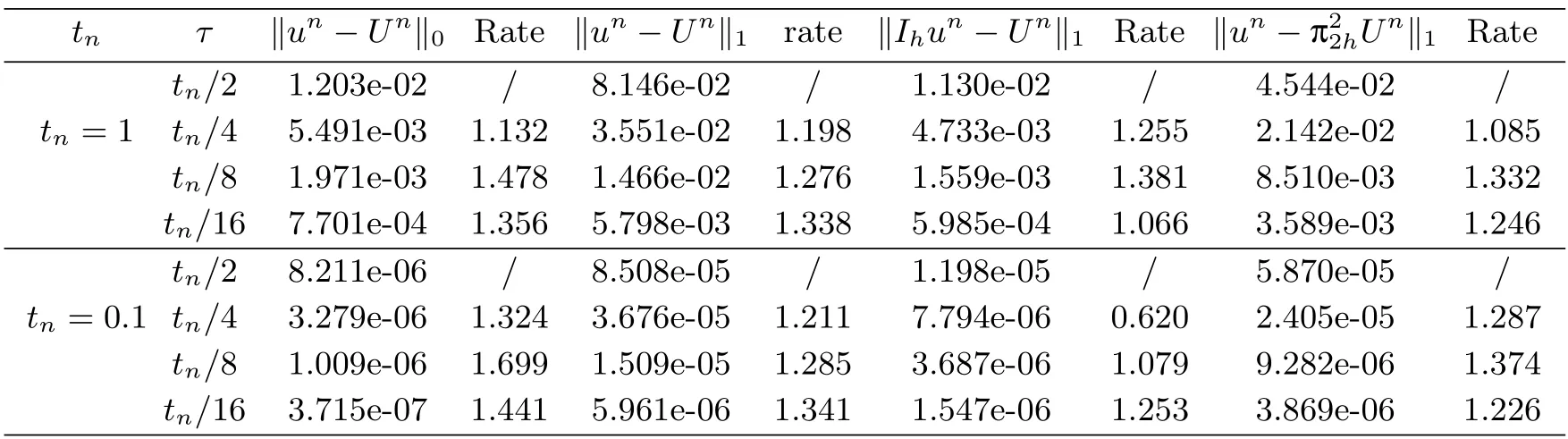
Tab.6.1 Errors and convergence rates of (2.5) with α=0.65,β=0.35 at tn=1,0.1

Tab.6.2 Errors and convergence rates of (2.5) with α=0.95,β=0.1 at tn=1,0.1

Tab.6.3 Errors and convergence rates of ‖un-Un‖0 with α=0.4,β=0.2,τ=0.001

Tab.6.4 Errors and convergence rates of ‖un-Un‖0 with α=0.7,β=0.4,τ=0.001

Tab.6.5 Errors and convergence rates of ‖un-Un‖1 with α=0.4,β=0.2,τ=0.001

Tab.6.6 Errors and convergence rates of ‖un-Un‖1 with α=0.7,β=0.4,τ=0.001

Tab.6.7 Errors and superclose rates of ‖Ihun-Un‖1 with α=0.4,β=0.2,τ=0.001

Tab.6.8 Errors and superclose rates of ‖Ihun-Un‖1 with α=0.7,β=0.4,τ=0.001
Tab.6.9 Errors and superconvergence rates of ‖un-Un‖1 with α=0.4,β=0.2,τ=0.001

Tab.6.9 Errors and superconvergence rates of ‖un-Un‖1 with α=0.4,β=0.2,τ=0.001
Tab.6.10 Errors and superconvergence rates of ‖un-Un‖1 with α=0.7,β=0.4,τ=0.001

Tab.6.10 Errors and superconvergence rates of ‖un-Un‖1 with α=0.7,β=0.4,τ=0.001
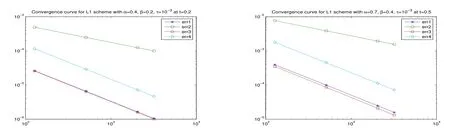
Fig.6.1 Error reduction results at t=0.2,t=0.5
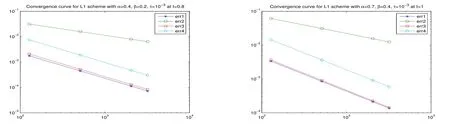
Fig.6.2 Error reduction results at t=0.8,t=1
Further,we also give the error reduction results in Figures 6.1 and 6.2 at different timestn=0.2,0.5,0.8,1,where err1,err2,err3 and err4 represent‖un-Un‖0,‖un-Un‖1,‖Ihun-
7.Conclusions
In this paper,based on the linear triangular FEM and theL1 approximation,we present an unconditionally stable fully-discrete scheme to numerically solve the multi-term time fractional diffusion equations with variable coefficient.Then,the superclose is deduced by combining with the interpolation operator and the projection.Meanwhile,the global superconvergence is obtained by using interpolation postprocessing operator.The provided numerical results demonstrate the effectiveness and high accuracy of the numerical approximate scheme.The proposed method of this paper can be applied to time-fractional wave equations.We will discuss superconvergence of FEMs for nonlinear multi-term time fractional equations and the high order time approximate scheme (see[24]) in near future.
- 應用數(shù)學的其它文章
- A Sufficient Condition for the Noncorrelation of Binary Pattern Sequences
- The Effects of θ on Stability in the θ-Milstein Method for Stochastic Differential Equations
- 基于分布式大數(shù)據(jù)的Expectile回歸分析
- 具有時滯的Lotka-Volterra食餌-捕食者成年種群模型的穩(wěn)定性分析
- 求解多目標優(yōu)化問題的非單調牛頓法的超線性收斂性
- 固定效應變系數(shù)空間自回歸面板數(shù)據(jù)模型的空間效應檢驗

