Exponential sine chaotification model for enhancing chaos and its hardware implementation

Rui Wang(王蕊) Meng-Yang Li(李孟洋) and Hai-Jun Luo(羅海軍)

1College of Physics and Electronic Engineering,Chongqing Normal University,Chongqing 401331,China

2National Center for Applied Mathematics in Chongqing,Chongqing 401331,China

3The University of Chicago,Chicago 60637,United States of America

Keywords: chaotic system,nonlinear system,image encryption,hardware implementation

1. Introduction

In 1963, Lorenz introduced the deterministic aperiodic flow model and the butterfly effect.[1]From then on, people have come to be aware of the field of chaos. Chaos theory,subsequently developed as a subfield of nonlinear science,[2]studies the behaviors of dynamical systems that have definite but unpredictable motions. The behavior of chaotic systems is determined by their initial states,yet it is impossible to predict long-term actions as they are sensitive to the slightest change in the initial states.[3]Those characteristics,such as initial state sensitivity,unpredictability,fractal dimension,and ergodicity,push chaotic systems to be widely studied and applied in many scenarios,such as personal information security,[4]communication systems,[5]and power systems.[6]

Presently, many chaotic systems have been developed for various applications, such as chaotic synchronization,[7,8]chaotic secure communication,[9]chaotic cryptography,[10,11]and chaotic neural networks.[12,13]Among them, chaotic secure communication and chaotic encryption[14,15]are among the hottest topics in the research of international electronic communications. For example,chaotic encryption utilizes the sequence generated by a chaotic system as keys for the encryption algorithm to run on. As chaotic systems are almost impossible to be predicted unless the exact system with the initial states is known, such an encryption method is very secure. However,existing chaotic systems are far from perfect.Firstly, with the help of computer technology, identifying the chaos becomes easier. Therefore,the current chaotic systems with their low complexity are easy to be cracked by discerning their initial states[16]or estimating their chaotic orbits.[17]Secondly, chaos degradation may occur when chaotic behaviors are simulated in finite precision. Some extremely approached states may overlap and appear to be precision truncated,[18]which causes the chaotic behaviors that originally had infinite states to degrade to inevitable periodic behaviors. Thirdly,existing chaotic maps show chaotic behaviors only in limited regions. Some perturbation on the input could lead to an unexpected chaotic result being replaced by a regular output. This perturbation could destroy the chaos and mean it is unable to play the role of encryption. These potential hazards harm the application of chaos,especially in the encryption area. Therefore, acquiring robust chaos with better chaotic performance can facilitate deeper research in the field of chaos and speed up the practical application of chaos.[19]

Much effort has been made to resolve the above problems and increase the complexity of existing chaotic systems.[20–25]For example, in Ref. [20], Liuet al.proposed a new coupled electro-optic chaotic system to conceal the time delay and enhance the complexity of chaos. They mixed the electrical signals by using nonlinear coupling functions. Luoet al.[21]introduced a novel image encryption algorithm based on double chaotic systems, which solved the limitation and vulnerability of a single chaotic map. In Ref. [22], Huanget al.took advantage of electrical mutual injection to improve the complexity and the security of chaotic communication systems. They used nonlinear transmission functions to conceal the time delay effect. Huaet al.in Ref. [23] proposed a chaotic model to enhance chaos and obtained robust results.They found a new model, a sine chaotification model, which can enhance the complexity of the current chaotic maps. They also used two maps to reach the required complexity for encryption safety.[24]In Ref.[25],Liu and Zhang improved plain text-related image encryption by constructing a special image,which can resist the existing chosen plaintext attack.

This paper introduces an exponential sine chaotificaton model(ESCM)to boost the complexity of the existing chaotic systems. Applying double nonlinear transformations to existing chaotic systems not only enhances their complexity but also achieves a larger chaotic range than before. The main achievements and novelties of this paper are as follows:(1)We introduced ESCM as a universal framework to enhance the chaos complexity. (2)The complexity of the ESCM was theoretically analyzed using the Lyapunov exponent(LE).(3)To exhibit the usability of ESCM, we applied ESCM to multidimensional (MD) chaotic maps, including the 1D logistic map, 2D H′enon map, and 3D Lorenz map. (4) We tested the chaos performance of the enhanced chaotic maps using theLEand the bifurcation diagram. We also compared the enhanced chaos performance with their seed maps. (5) To demonstrate the practicability and simplicity of ESCM in a hardware environment, we constructed and tested the circuits of the enhanced chaotic maps in a digital signal processor(DSP).(7)We applied ESCM to image encryption and investigated its effectiveness.

The remainder of this paper is organized as follows. Section 2 presents the proposed ESCM and analyzes its chaos complexity theoretically. Section 3 applies ESCM to a logistic map,H′enon map,and Lorenz map. We also discussed the chaotic dynamics of these chaotic maps. Section 4 validates its hardware availability using the DSP. In Section 5, we applied the enhanced Lorenz chaotic map to implement image encryption and analyzed the encryption effect. Finally, Section 6 concludes this paper.

2. Exp-sine chaotification model

This section proposes ESCM and analyses its chaos complexity.

2.1. Concept of ESCM

The proposed ESCM is designed to enhance the complexity of existing chaos. Using double nonlinear transformations and applying them to the chaotic maps, ESCM can significantly enhance the chaos complexity. The structure’s plot is shown in Fig.1.

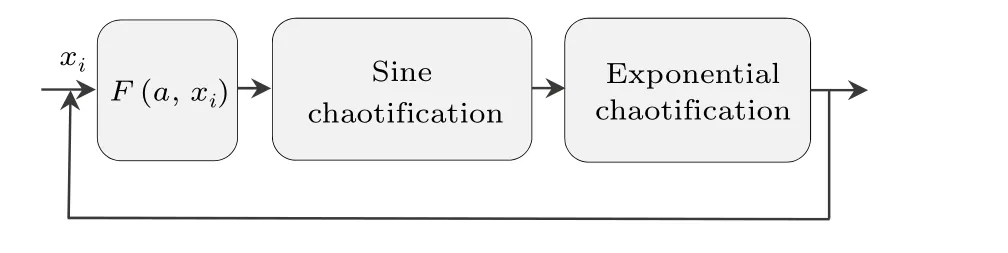
Fig.1. Structure of the ESCM.

HereF(a,xi) is an existing chaotic map called a seed map, whereais a control parameter, andxiis the input. The output esin(πF(a,xi))is used as the input for the next iteration.

We can use a mathematical equation to describe ESCM as

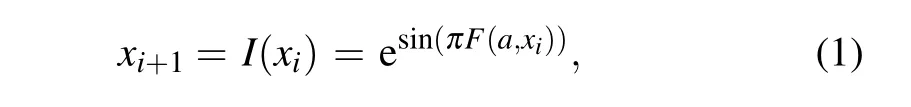
whereais a control parameter.

The exponent function,as well as the sine function,have complex nonlinear properties. Double nonlinear transformations enhance the complexity of existing chaos. The effect of ESCM in improving chaotic performance can be theoretically validated by using theLEas a standard. In this paper, we used ESCM as a chaotification model to improve the performance of chaos. The properties of ESCM are as follows. (1)It is an effective model that can enhance chaotic performance.(2) Compared with the seed map, the enhanced map owns chaotic behaviors in quite a large parameter range. (3)The enhanced map overcomes the drawbacks of seed maps entering periodic motion occasionally. (4)This model is applicable to both discrete and continuous chaotic systems. (5)Users have freewill to choose any dimension map to work as the seed map.

These properties will be verified in the following parts.

2.2. Chaos complexity analysis

Due to the singularity and complexity of the chaos system, there is no unified definition of chaos. To quantitatively characterize the sensitivity of the chaotic system to the initial value, theLEcan work as a standard. TheLEis one of the most widely used criteria accepted by researchers. TheLE[26]refers to the average rate of exponential separation or convergence of two trajectories close to each other in phase space over time. IfLE>0, we can consider that it enters chaos states.

To calculate theLEof ESCM,we supposex0is the initial value of the chaotic systemF(a,xi) in Eq. (1), and we havey0=x0+εwhich differs withx0by an infinitesimal positiveε.After one iteration by Eq.(1),the difference betweenx1andy1can be calculated as

From the above,the existing chaotic map through ESCM could have largerLEthan before,which means they have better chaotic performance in more extensive parameter ranges.Even with seed maps that do not have chaotic behaviors, the enhanced map may also show chaotic traits through the transformation of the ESCM.This proves that the proposed ESCM can enhance the chaos performance in a more extensive range.

3. Typical examples of an enhanced chaotic map

To verify the performance of ESCM,we shall apply it to three example maps with different dimensions. They are a 1D logistic map,a 2D H′enon map,and 3D Lorenz map. We will also analyze the chaotic dynamics of the enhanced map.

The logistic map[27]is derived from a demographic dynamics system designed to stimulate people’s growth, and it is one of the most widely used nonlinear dynamical discrete chaotic mapping systems. It seems too simple and deterministic but has complicated dynamical behaviors.Its mathematical mapping equation can be defined as

3.1. Enhanced logistic map

Definition When applying ESCM to a logistic map, it means theF(a,xi) in Eq. (1) is replaced by a logistic map in Eq. (10). Its new mathematical mapping equation can be defined as

Bifurcation diagram The bifurcation phenomenon is a significant characteristic of nonlinear systems. Bifurcation refers to the phenomenon that a slight change in the vicinity of a parameter causes a sudden change in the phase space orbital topological structure. A bifurcation diagram is a direct description of the chaotic state of the system.[29]

Figure 2 describes the bifurcation diagram of previous maps and their enhanced maps. Figure 2(a) plots the bifurcation diagram of the logistic map when its control parameterμ ∈[0,4]. Here, 410 iterations were performed. In order to make the iteration sufficient,the initial 400 times were discarded. As shown in Fig. 2(a), it is apparent that the logistic map is in the period-doubling bifurcation state whenμ ∈[0,3.6]and enters chaotic states whenμ ∈[3.6,4]. Even within the range of[3.6,4],there are still some periodic areas.With a slight disturbance, it will enter the periodic motions.Its outputs are limited in[0,1],while figure 2(d)represents the bifurcation diagram of the logistic map through ESCM when its control parameter ?μ ∈[0,1000]. It is clear that the logistic map through ESCM has outputs within the range[0.4,2.8],and these outputs distribute in the whole data range. In other words, the enhanced logistic map obtains superior complex dynamic behavior in a much larger range compared to its seed map,which has weak chaos in small parameter ranges.

Lyapunov exponentLErefers to the average exponential separation or convergence of two orbitals close to each other in phase space over time.[26]It can represent the initial sensitivity when the dynamic system evolves. For nonlinear systems,if theLEis negative,the dynamical system is stable and shrinks in phase space, while positiveLErepresents the phase volume of the system that expands and folds continuously in one direction,in other words,the system is chaotic.

Figure 3 depicts theLEof improved chaos and their seed maps. For comparison convenience, we have normalized the process. As shown in Fig.3(a),the enhanced logistic map enters a chaos state earlier than before. The previous map enters chaos when its control parameter is over 3.6,yet the enhanced chaos enters chaos from the start. TheLEof the enhanced logistic map increases as the control parameter increases. That also means the complexity of the enhanced seed map also increases. As depicted in Fig.3(a),although the control parameter is over 3.6, itsLEof the logistic map may also be less than 0 occasionally. In contrast,theLEof the enhanced logistic map is always positive,which indicates that it has complex dynamical behavior.It is clear that through ESCM,the logistic map obtains dynamic behavior in wider ranges.

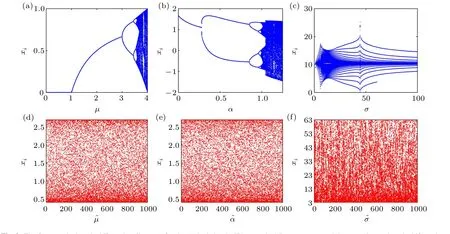
Fig.2. The first row depicts the bifurcation diagrams for the(a)logistic,(b)H′enon and(c)Lorenz maps,and the second row plots the bifurcation diagrams for their enhanced maps.

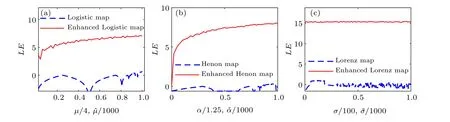
Fig.3. The LEs of the(a)logistic and enhanced logistic map,(b)H′enon and enhanced H′enon map,and(c)Lorenz map and improved Lorenz map.

3.2. Enhanced H′enon map

Definition When applying ESCM to the H′enon map, it means theF(a,xi) in Eq. (1) is replaced by the H′enon map in Eq. (11). Its new mathematical mapping equation can be defined as

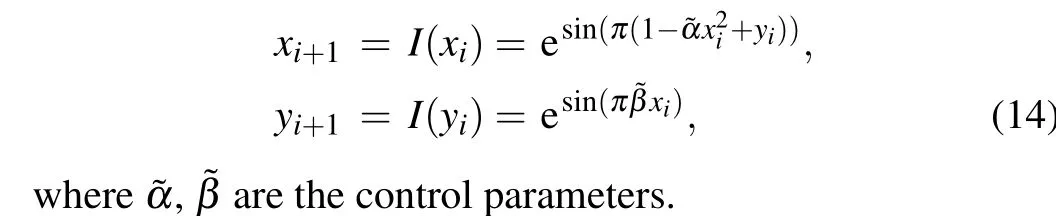
Bifurcation diagram Figure 2(b)shows the bifurcation diagrams of the H′enon map. Since the 2D H′enon map has two control parameters, to obtain a straightforward comparison effect,we only plot the bifurcation diagrams of the H′enon chaotic maps when the control parameterβis fixed at 0.4 and selectαas the main control parameter within[0,1.25]. Here,200 iterations were performed. To make the iteration sufficient,the initial 50 times were discarded. Whenα ∈[1,1.25],the dynamical systems show complicated behavior. The outputs of the H′enon map are confined in the range of[0,2]. Figure 2(e)shows its enhanced bifurcation diagrams. Their initial state values are all set as(0,0). Also,200 iterations were performed, and the initial 190 times were discarded at the same time to ensure the result was satisfying. One can see that the trajectory of the enhanced H′enon map is distributed in all data ranges. At the same time, its outputs occasionally spread all over in the range of[0.4,2.7].

Lyapunov exponent For the sake of presentation, here we set the control parameterβ=0.3. As shown in Fig.3(b),the H′enon map enters chaos whenα>1.07. It is clear that the H′enon chaotic maps enter the chaotic state only in a small range,which could impair the effect of encryption. Therefore,the original seed map is not robust. Through ESCM,it enters chaos from the start and has more significant complexity than its seed map. Along with the increase of the control parameter,theLEof the enhanced H′enon map becomes larger. That means the complexity of the enhanced H′enon map becomes larger as the control parameter increases.

3.3. Enhanced Lorenz map

Definition When applying ESCM to the Lorenz map,theF(a,xi)in Eq.(1)is replaced by the Lorenz map in Eq.(12).

Bifurcation diagram The Lorenz map is a 3D chaotic map with three control parameters. Both initial values are set as(1,1,1). Figure 2(c)shows the bifurcation diagrams of the Lorenz map. We fixed two control parameters,ωandψ, to directly compare and observe their motion trials. As depicted in Fig. 2(c), it is obvious that the chaotic performance of the Lorenz map is frail with the control parameterσincreasing.It only presents complex dynamic behaviours in small parameter ranges. The outputs of the Lorenz map are restricted at[0,20]. Figure 2(f)shows the enhanced Lorenz map’s bifurcation diagrams.Exhibited in the image,it is almost all in chaos.When the parameter is within [0,1000], its outputs spread in[3,63]irregularly. Thus,the proposed ESCM can significantly enhance the chaos of the Lorenz map. The enhanced Lorenz map shows robust and complex dynamical behavior.

Lyapunov exponent As depicted in Fig.3(c),only small parts of this system are in chaos. When the control parameter is within[5,18],theLEof the Lorenz map is positive,and the system is in chaos. In other regions, theLEjumps and changes randomly, which harms the practical application of chaos. When we compared the enhanced Lorenz map with its seed map,it is obvious that the performance improved significantly, and at the same time, it is all in chaos states. From Fig. 3(c), no matter how the control parameters change, theLEof the enhanced Lorenz map is always positive and obtains high values. That means ESCM improves the complexity of the seed map efficiently.

4. Hardware implementation

4.1. Hardware structure setting

We selected the enhanced logistic, H′enon, and Lorenz maps to verify hardware operability.

Design of DSP In some particular application scenarios,the chaotic system must be implemented in digital platforms.The DSP is a new hardware environment to simulate a chaotic system. For example, figure 4 plots the structure diagram of the hardware implementation of the improved H′enon map.There are three main components: the chaotic function generator,the counter,and feedback. The chaotic equation through the ESCM would receive the control signals and initial current valuex0,y0. Iterations are calculated by the counter and are implemented with feedback. Here,the function is the original chaotic equation through ESCM.Then,we put the result to the PWM output port of the DSP and then change the duty cycle of the PWM. Through the filter, which works as a digital-toanalog converter, we can get an analog output and input the value to the display device.

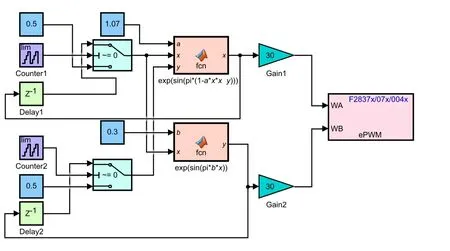
Fig. 4. Structure diagram of a hardware implementation of the improved H′enon map.

Implementation results Here, we present the implemented results of the enhanced logistic, H′enon, and Lorenz map. Figure 5 shows the DSP implementation environment. Figure 6 depicts the DSP implementation result shown in the oscilloscope. The logistic map initial state was set as (x0,?μ) = (0.1,10). The initial state of the H′enon map was set in (x0,y0,?α,?β) = (0.5,0.5,1.07,0.3). Here we set the initial state of the Lorenz map at (x0,y0,z0,?σ,?ω,?ψ) =(0.5,0.5,0.5,10,28,8/3). With observation by the oscilloscope,the three enhanced chaotic maps can generate complex random sequences. So, we can conclude that this enhanced model is suitable for practical application.

Fig.5. Hardware prototype developed in DSP implementation.

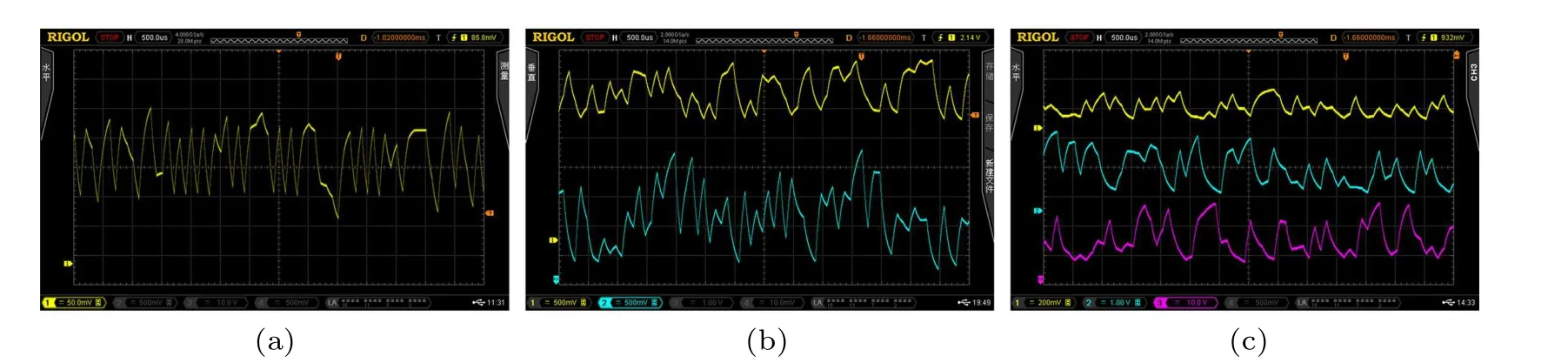
Fig.6. DSP simulation results for the three enhanced chaotic maps in the oscilloscope. (a)The enhanced logistic,(b)the enhanced H′enon,(c)the enhanced Lorenz maps.

5. Application of ESCM in image encryption

Currently, chaotic sequence encryption has been listed as an important research frontier of modern cryptography.Chaotic encryption is also referred to as digital sequence encryption. The chaos system can provide randomness, correlation, and a complex pseudorandom sequence. The signal is produced through a chaos map, and thus is nearly impossible for hackers to decode without knowing the initial key value.To satisfy the need for privacy protection, the chaotic image encryption technique has been studied intensively.[30,31]Since chaotic systems have been demonstrated to have a profound impact on encryption technology,we applied ESCM to image encryption.To highlight the effect of ESCM,we compared the effect of the enhanced map with its seed map.

5.1. Proposed image encryption

Here, we applied ESCM to the Lorenz map. We made use of the sequence generated by an enhanced chaotic system to implement image encryption.Unlike traditional encryption,chaotic encryption is dynamic encryption, and it has properties such as concealment, unpredictability, and resistance to exhaustion.

5.2. Encryption process

This paper uses the enhanced Lorenz system,permutation-based on Arnold transformation, and twice finite field diffusion to realize the image encryption scheme.The encryption process is described as follows.

Step 2: Encryption of the graph

With the generated permutation sequenceAandB, we will now swap the pixels in the graph according to the position given byAandB. We exchange the pixel’s position (1,i)of the original picture to its new position(p,q)by performing Arnold transformation. When consideringqmerely, the exchange between pixel points (1,i) and (1,q) can be constructed. At the same time,ABis regarded as a new random number and is still marked asA, thenqbecomesq=B+Ai.The performance of the permutation is simulated as in Fig.7.

Next,usingS1 andS2,we can forward diffuse and reverse diffuse every pixel using the XOR operation. Notice that for a colour graph,every channel(RGB)needs to go through encryption. The process of diffusion is shown in Fig.8.

The original graph is now safe as encrypted into a “random”graph.

Step 3: Decrypt the graph

To decipher the encrypted graph,we need to run the steps backward i.e.,re-run the XOR operation usingS2 andS1,and then swap the pixels usingBandA.Thus,we achieve the plain text graph as desired.

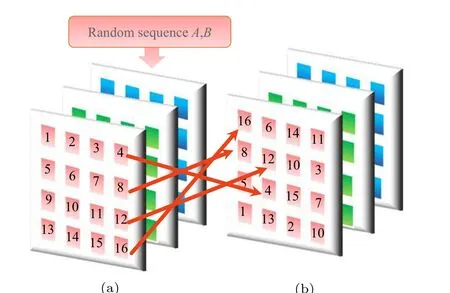
Fig.7. The first step in encryption–confusion. (a)The raw information of plain images. (b)The information through the confusion process.

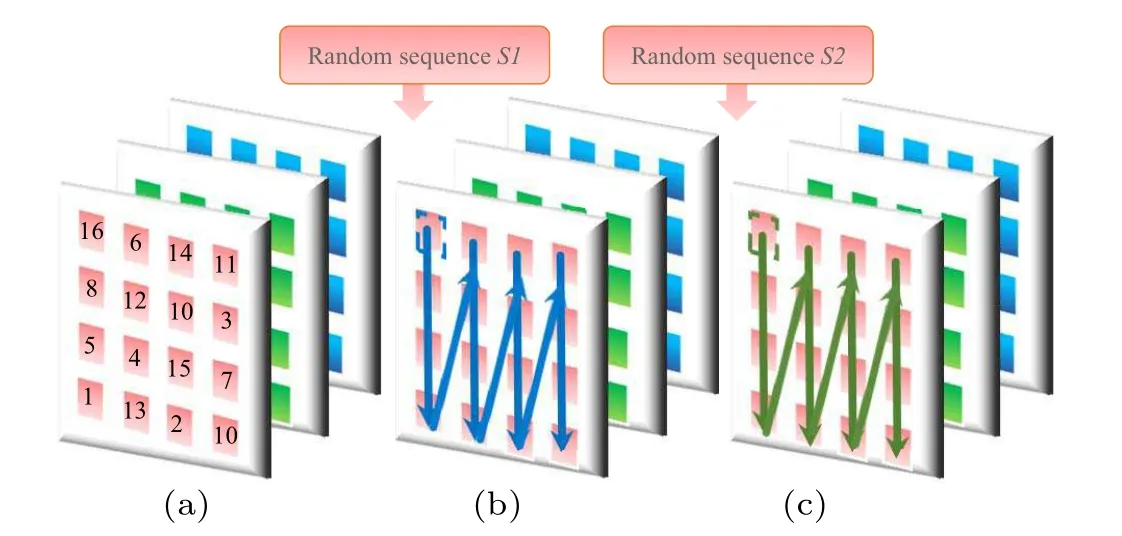
Fig. 8. The diffusion process. (a) The information through the confusing process. (b)The information diffused through random sequence S1. It is a forward diffusion. (c) The information diffused through random sequence S2. It is a counter diffusion.

5.3. Simulation results

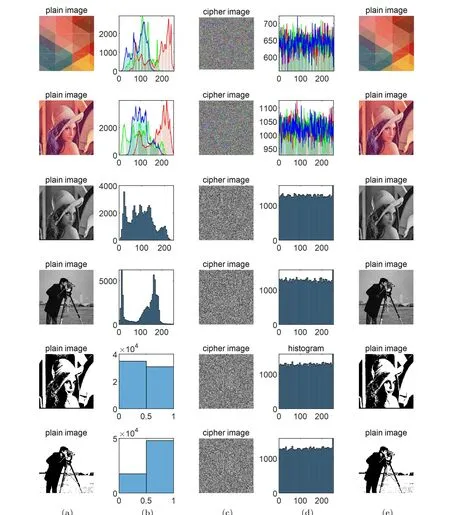
Fig. 9. Panel (a) presents color diagrams, gray diagrams, and binary diagrams. Panel (b) depicts the histogram of the original images. Panel (c)depicts the encrypted pictures through the enhanced map. Panel (d) describes the histogram of the encrypted images. Panel (e) describes the decrypted images.

The image histogram reflects the statistical characteristics of image pixel distribution. We used drawing software to display the picture’s histogram. A practical and convenient image encryption algorithm should be capable of encrypting different types of pictures in order to fit different security requirements. As shown in Fig.9,three different types of images are encrypted. Figure 9(a) represents two color images, two grayscale images, and two binary images.Figure 9(b) simulates their corresponding image histograms.By observing their histograms,an important amount of information can be deduced about the pictures. Through ESCM,the original images in Fig.9(a)become the encrypted images in Fig. 9(c). We found that images through chaotic encryption have a higher complexity. Figure 9(d) describes the histograms of the encrypted images. This encryption hides the original image’s statistical properties splendidly and can defend a statistical attack based on image pixel values. The obvious statistical features of the original image have been hidden,replaced by the average distribution of the encrypted histogram. It is hard to find any regularity from this histogram.Through the correct key, it is easy to retrieve the information just as in Fig. 9(e). To compare the effect of encryption after the ESCM,here we encrypted the gray images through the Lorenz map as shown in Fig. 10. It is obvious that the encryption could not hide the statistical features of the original images perfectly. From Fig.10(c),it is not hard to vaguely see the general shape of the original picture. At the same time,the histograms of the encrypted images are not flat compared with Fig. 9(d), which means this encryption effect is worse than before. Figure 11 presents 3D visualization of the plain and cipher image. The first row depicts all pixels in the red,green,and blue color planes in the plain image. Each different color component has its distribution regularities. By contrast, the encrypted images hide the distribution rule of the pixels,so all pixels in the red, green, and blue color planes are distributed uniformly in the encrypted images. In other words,the ESCM can encrypt original images as cipher images with high performance. Compared to traditional encryption, chaotic encryption has higher complexity and hides the features of the original image perfectly. This encryption scheme contributes to chaotic secure communication and chaotic encryption, which is currently being widely researched.

Fig. 10. Panel (a) presents the gray diagrams. Panel (b) depicts the histogram of the original images. Panel (c) depicts the encrypted pictures through the Lorenz map. Panel(d)describes the histogram of the encrypted images. Panel(e)describes the decrypted images.

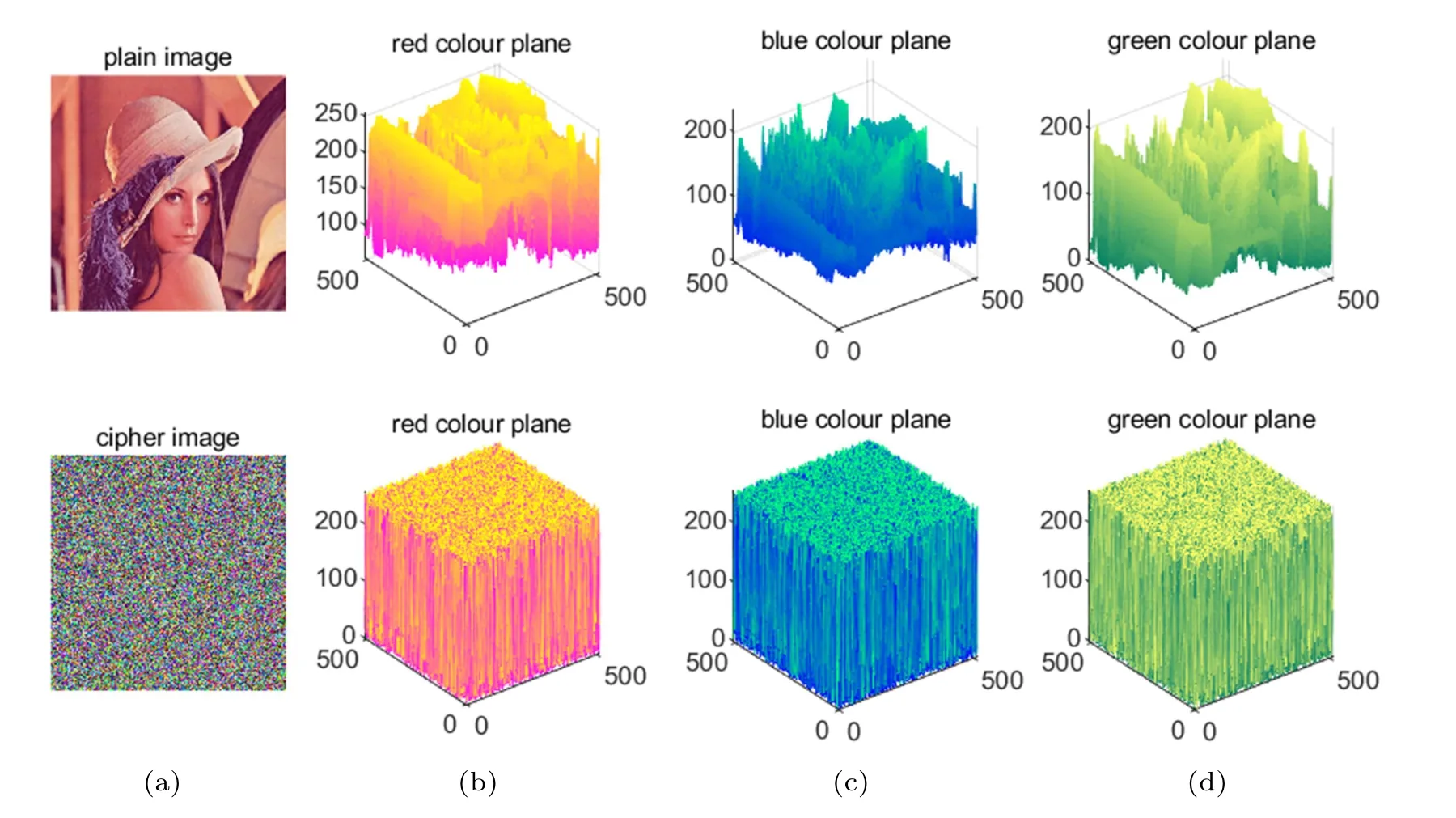
Fig. 11. Panel (a) presents original and encrypted images. Panel (b) depicts the red color plane of the images. Panel (c) depicts the green color plane of the images. Panel(d)depicts the blue color plane of the images.

6. Conclusion

This paper proposed an ESCM to enhance the complexity of existing chaotic maps. The ESCM uses a double nonlinear chaotic transform, including an exponential and a sine function,to enhance chaos complexity. The dynamical behavior of ESCM is verified using the principle of theLE.The resulting enhanced map of the ESCM has better chaos complexity and a much larger chaotic range than an original chaotic map. We applied it to three different dimensional chaotic maps,namely the logistic map,H′enon map,and Lorenz map,and discussed their dynamic behavior. The results confirmed that the enhanced chaos has better performance than their seed map. We used DSP to implement chaos circuits,demonstrating the simplicity of the ESCM in hardware devices. Lastly, to exhibit the practical application of an enhanced chaos map, we applied it to image encryption. The results show that chaotic image encryption hides the information of the original image effectively.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 51507023), Chongqing Municipal Natural Science Foundation (Grant No. cstc2020jcyjmsxmX0726),and the Science and Technology Research Program of Chongqing Municipal Education Commission(Grant No.KJZD-K202100506).