On the electron sheath theory and its applications in plasma-surface interactions
Guangyu SUN(孫光宇) ,Shu ZHANG(張舒) ,Anbang SUN(孫安邦)and Guanjun ZHANG (張冠軍)
State Key Laboratory of Electrical Insulation and Power Equipment, School of Electrical Engineering,Xi’an Jiaotong University, Xi’an 710049, People’s Republic of China
Abstract In this work, an improved understanding of electron sheath theory is provided using both fluid and kinetic approaches while elaborating on their implications for plasma-surface interactions.A fluid model is proposed considering the electron presheath structure, avoiding the singularity in electron sheath Child-Langmuir law which overestimates the sheath potential. Subsequently, a kinetic model of electron sheath is established,showing considerably different sheath profiles in respect to the fluid model due to non-Maxwellian electron velocity distribution function and finite ion temperature.The kinetic model is then further generalized and involves a more realistic truncated ion velocity distribution function. It is demonstrated that such a distribution function yields a super-thermal electron sheath whose entering velocity at the sheath edge is greater than the Bohm criterion prediction. Furthermore, an attempt is made to describe the electron presheath-sheath coupling within the kinetic framework, showing a necessary compromise between a realistic sheath entrance and the inclusion of kinetic effects. Finally, the secondary electron emissions induced by sheath-accelerated plasma electrons in an electron sheath are analysed and the influence of backscattering is discussed.
Keywords: plasma-surface interaction, plasma sheath, secondary electron emission, Child-Langmuir law
1. Introduction
The sheath is a space-charge region commonly formed at the edge of plasma which breaks up the quasi-neutrality and shields the bulk plasma from a solid boundary. The sheath plays an essential role in confined plasma research, and in particular in plasma-surface interactions, such as in plasma processing, plasma propulsion engines, magnetic-confined fusion,dust particles,plasma diagnostics,etc[1-9].A classic Debye sheath (also called an ion sheath) appears when a floating slab is injected into a plasma.Initially,more electrons than ions enter the board due to their higher mobility,leaving net positive charges in the gradually formed ‘sheath’ region while depositing negative charges on the solid material,which in turn mitigates the electron flow until the plasma current is balanced at the solid wall.

Apart from the Langmuir probe sweep in the electron saturation region, electron sheaths also appear in a variety other scenarios, such as in dusty plasma particle circulation,scrape-off layer diagnostics, planet surfaces, spacecraft probes, anode ablation by arc, and some transient processes[14-17]. Nonetheless, there are fewer related studies on electron sheaths than on ion sheaths, and electron sheath counterparts of some well-developed models for ion sheaths have yet to be established.
The current study of electron sheaths is primarily motivated by the pragmatic demand for probe diagnostics. For simplicity, a probe biased more positively than the plasma is assumed to collect the full electron current from the electron sheath, while ions are neglected in the sheath. The electron velocity distribution function (EVDF) of the sheath entrance is trivially regarded as half-Maxwellian and no presheath structure is considered [18]. These assumptions greatly facilitate the implementation of electron sheath physics into probe calibration.However,recent progress in electron sheath theories has shown that the underlying physics is far from simple. A simulation by Yee et al proved that a presheath exists for electron sheaths, which accelerates the plasma electrons up to thermal velocity at the sheath entrance [19].The presheath size of an electron sheath is larger than that of ion presheaths and extends deeply into the bulk plasma.Also,a comprehensive presheath theory was proposed by Brett et al based on fluid equations [20]. It was shown that electrons in presheaths are mainly driven by the pressure gradient, and that the accelerated electrons give rise to fluctuations due to ion acoustic instabilities.Instabilities in electron sheaths were also investigated experimentally by Stenzel et al [21, 22].Additionally,the transition between an electron sheath and an ion sheath was reproduced in simulation by varying electrode bias potential [23]. The electron sheath can even be enclosed by an ion presheath by surrounding a metallic electrode with dielectric material [24].
Existing electron sheath theories are mostly based on a fluid model and mainly focus on the presheath region and the sheath is only treated as a boundary condition.A fluid model can be applied in the presheath region where collisionality is sufficiently large to form a near-Maxwellian distribution.However,the scenarios in the electron sheath region are more complex. In the present article, electron sheath theories in low-temperature, low pressure, unmagnetized plasma are investigated. First of all, the newly discovered electronentering velocity at the sheath edge inevitably yields a truncated EVDF at the sheath entrance.The ion-entering velocity in the ion sheath edge barely matters since the initial ion energy is far lower than the ion sheath potential energy,whereas this is not the case in the electron sheath.In addition,the plasma electrons are accelerated by the sheath potential and collide on the electrode with greater energy compared with the electrons in the ion sheath, inducing secondary electron emission (SEE). This may alter the current balance since both emitted electrons and plasma electrons contribute to the measured current, yet this effect has drawn little attention. The present work attempts to address these issues on theoretical grounds and discusses their pertinent implications in plasma-surface interactions.
The article’s structure is as follows. In section 2, the Child-Langmuir law for electron sheaths is reviewed, and is compared with an updated fluid model of electron sheaths.Section 3 provides comprehensive kinetic modeling of an electron sheath, involving an electron and ion velocity distribution function (IVDF) and the influence of electron-ion temperature ratio. In section 4, the SEE caused by sheathaccelerated electrons is implemented in the electron sheath model. Concluding remarks are given in section 5.
2. Fluid model of an electron sheath
2.1. Review of the Child-Langmuir model in electron sheaths


wherexishis ion sheath length andλDeis electron Debye length. Detailed derivations are available in numerous references and are not repeated here [10, 12]. In the case of an electron sheath, the potential relative to sheath edge is positive and electrons are accelerated while ions are de-accelerated, so the electron sheath is assumed to be ion-free. The Poisson equation is written as:


Another issue of the above deductions is the neglected EVDF. Equation (4) implicitly regards electrons as a monoenergetic beam. Though this is also used in the derivation of ion sheath Child-Langmuir law, one must realize that the electron temperature is far greater than ion temperature for a typical cold plasma discharge; thus, the omission of electron kinetic effects in an electron sheath will introduce larger discrepancies compared with neglecting the IVDF in an ion sheath. Treatment of the EVDF is discussed in section 3.
2.2. Revised fluid model of an electron sheath
In this section, an electron sheath fluid model that considers the electron presheath is introduced. The derivation below is based on previous studies of the electron-entering velocity in the electron sheath, but a different conclusion about the electron sheath structure is obtained, due to a distinct treatment of Poisson equation [20]. To include the influence of electron-entering velocity, it is intuitive to write down the electron fluid equations in the sheath and regard the entering velocity as a boundary condition. To begin with, the particle and momentum balance of electrons in the sheath is given as
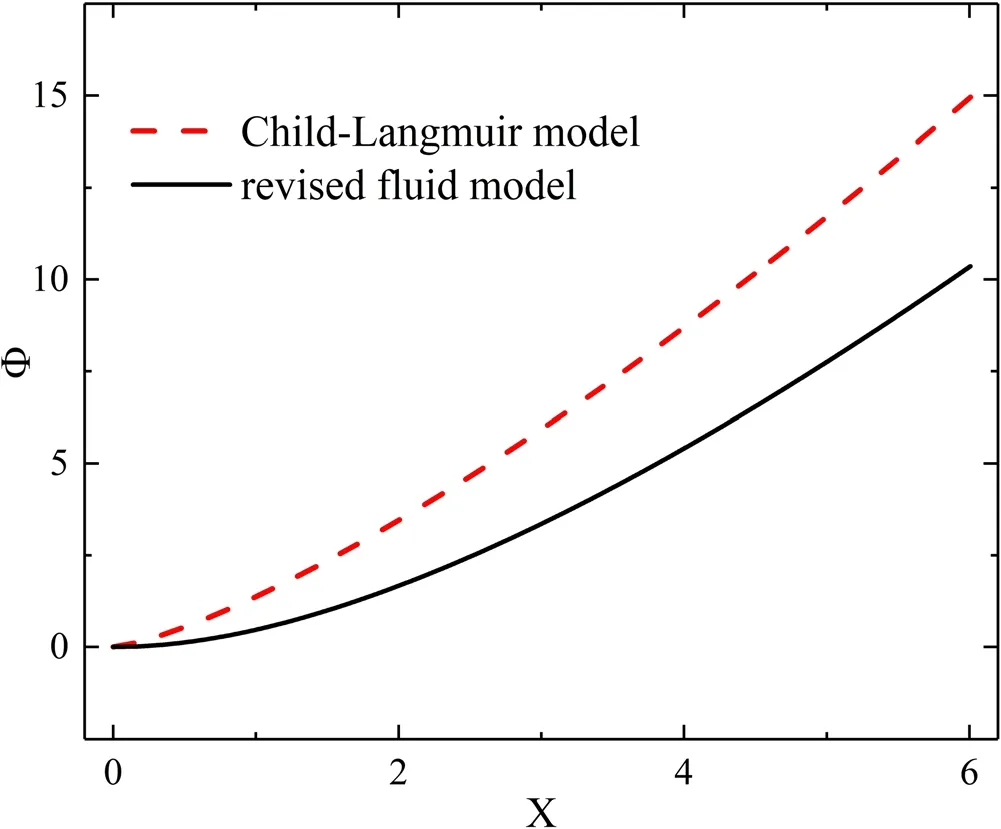
Figure 1. Comparison of potential distribution in electron sheath based on the Child-Langmuir law and the revised fluid model.Φ is the normalized potential and X is the normalized position. The Child-Langmuir model overestimates the sheath potential.
follows:

whereueois the electron fluid velocity at the sheath edge and is treated as the boundary condition; the potential at the sheath edge is chosen as 0. It is noted that here the temperature gradient term is dropped, and the isothermal relation is adopted. The resulting equation is:

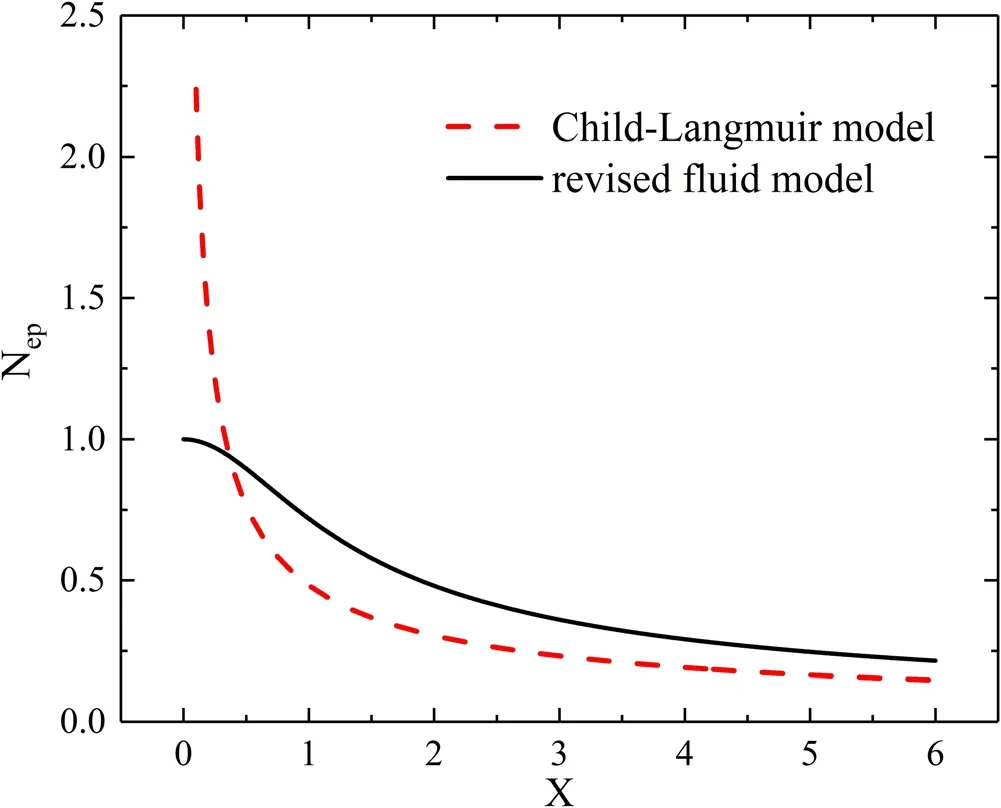
Figure 2.Normalized electron density distribution in the sheath region predicted by the Child-Langmuir model and the revised fluid model. The Child-Langmuir model gives infinite density at X= 0.The part of the Child-Langmuir solution curve in the vicinity of the singularity is not shown for better figure scaling. The Child-Langmuir law predicts lower electron density, except near X= 0.
Equation (12) can be solved by rewriting it in the form of a Lambert W function and taking the asymptotic limit at large potential. More details on the solution of this form of equation were given in the work of Brett et al[20],here the result is given directly:

The potential distributions given by equations (8), (16)and the previous solution in [20] are shown in figure 1(named separately as the Child-Langmuir model, which is the same as the solution in[20],and the revised fluid model).Generally, the Child-Langmuir solution slightly overestimates the electron sheath potential.
The electron density distributions in the sheath predicted by the Child-Langmuir model and the revised fluid model are shown in figure 2. The Child-Langmuir model generally underestimates the electron density in locations far away from the sheath edge. One major flaw of the Child-Langmuir model is that there is a density singularity atX= 0 due to neglecting the electron-entering velocity at the sheath edge.Section 3.1 will show that the singularity can also be avoided by considering electron kinetic effects even without involving the electron-entering velocity at the sheath edge.

3. Kinetic model of an electron sheath
3.1. Kinetic model without a presheath
In section 2, electron fluid equations are used to derive the electron sheath solution.However,the exact EVDF inside the sheath is not thoroughly considered. To illustrate the influence of kinetic effects on the electron sheath solution, the following kinetic model of an electron sheath is constructed.In addition, IVDF is involved to investigate the influence of nonzero ion temperature for more general applications of the theory.
To begin with, the electron and ion densities inside the sheath should be determined. The electrons are accelerated due to increasing sheath potential towards the electrode;hence, a velocity lower bound appears when integrating the half-Maxwellian EVDF, which gives the following electron density:

The ions are repelled by the electron sheath potential,just like the electrons in an ion sheath. If the force posed by the electric field is balanced by the pressure gradient force, the Boltzmann distribution can be used to derive the following ion density:
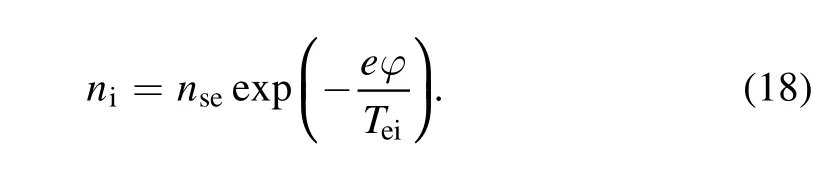
The Poisson equation can therefore be written as:

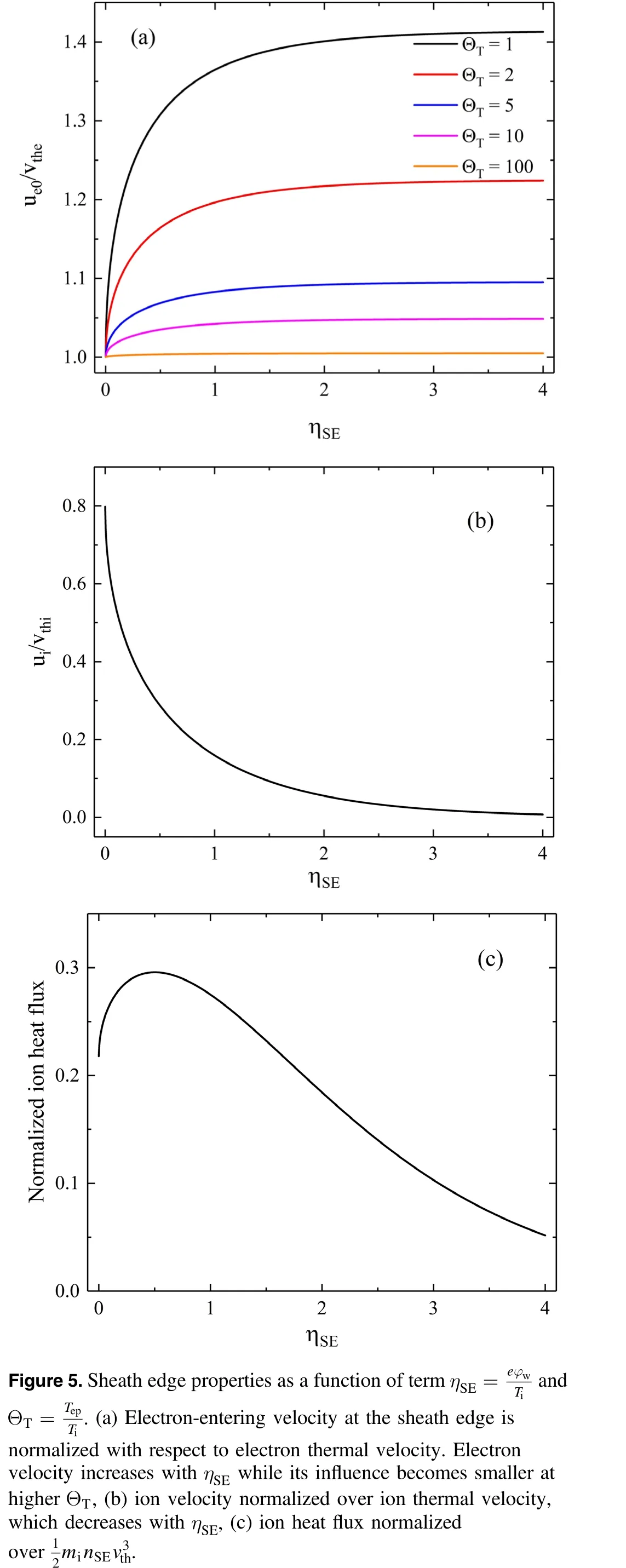
Calculated results with different Φwvalues are shown in figure 3(a) and are compared with the Child-Langmuir prediction and the fluid model with a presheath.One can find that the sheath size given by the kinetic model is typically above that given by the Child-Langmuir solution for a smaller electron sheath and is below the Child-Langmuir solution for a larger electron sheath and a higher electrode potential.Considering that an electron presheath makes the electron sheath potential smaller for a fixed sheath size, it is always below the kinetic model prediction except at very high electrode potential levels. Profiles of sheath potential distribution in space are remarkably different. In general, the kinetic model predicts a shorter sheath size at a fixed electrode potential, and its space potential profile is higher than the Child-Langmuir solution.
The influence of ion temperature is shown in figure 3(b).It is clear that the ion temperature only exerts a minor influence on the shape of the potential profile, and a high ion temperature slightly decreases the size of the electron sheath.The potential profile becomes virtually insensitive to ion temperature after the value ofΘTexceeds around 5. Consequently, in typical low-temperature plasma applications, the influence of ion temperature on potential distribution is marginal. The calculated electron and ion density distributions in the sheath predicted by the kinetic model are compared with the Child-Langmuir model in figure 4. The electron and ion densities are normalized with respect to the sheath edge density:


Figure 3.(a)Comparison of sheath potential distributions given by the adopted kinetic model,the Child-Langmuir law and the fluid model with a presheath. X is normalized position andΦ is normalized potential.(b)Influence of electron-ion temperature ratio on sheath potential distribution. The influence is negligible afterΘT surpasses 5.
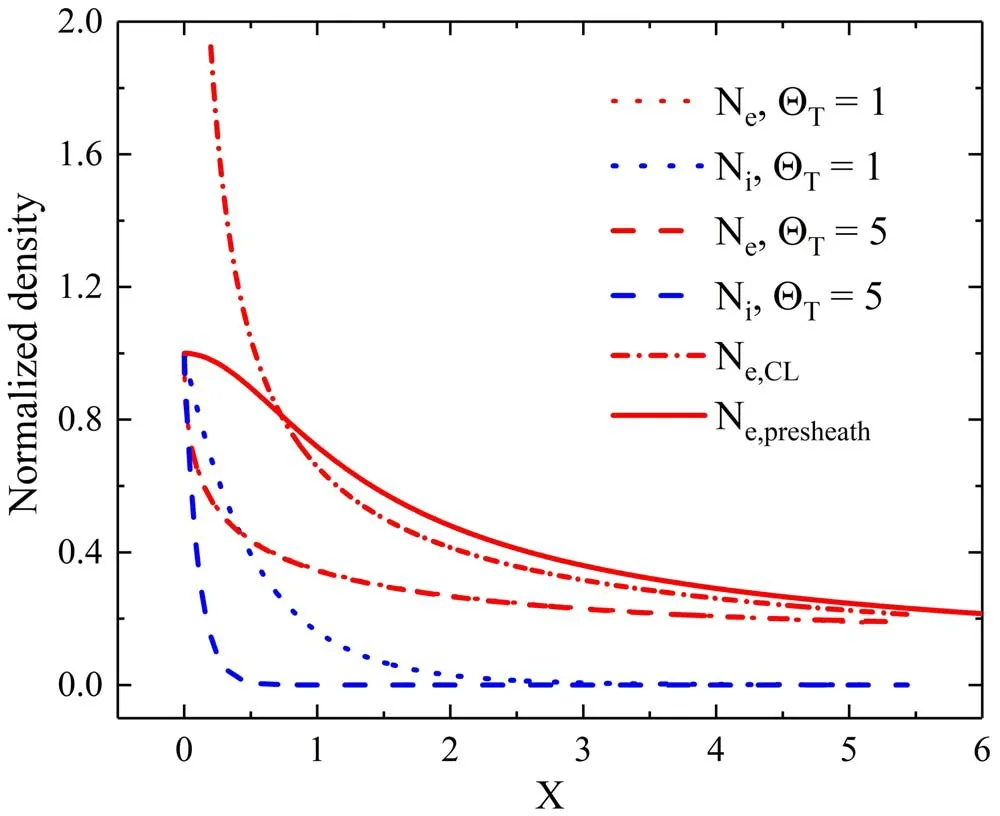
Figure 4.Electron and ion densities given by the kinetic model, the Child-Langmuir model and the fluid model with an electron presheath. Different electron-ion temperature ratios are used to illustrate influence of ion temperature. The part of Child-Langmuir solution curve in the vicinity of the singularity is not shown for better figure scaling. The electron density profile is not sensitive to ΘT while ion density proflies change remarkably withΘ T.
Generally, the kinetic model gives a lower electron density compared with the Child-Langmuir model and the fluid model considering an electron presheath, suggesting an overestimation of plasma density when using fluid models;the ion density is ignored in fluid models. The kinetic model without an electron presheath (hence zero entering velocity)and the fluid model considering an electron presheath avoids the singularity atX= 0.The electron density profile is barely influenced by the change ofΘT,whereas the ion density profile changes remarkably withΘT.Here,the ion Boltzmann distribution is adopted, whereas in practice, some energetic ions might penetrate the electron sheath and arrive at electrodes, which is increasingly obvious for lowΘT.These ions will not return to the plasma and inevitably leaves an IVDF dissipated at a high-velocity tail [29]. Also, the ion density could be slightly higher than electron density in the vicinity of the sheath edge. This actually contradicts the general Bohm criterion, and is due to the neglect of the electron presheath structure in the kinetic model. Further analyses regarding a more accurate IVDF and the influence of electron presheath structure on the sheath solution will be given in sections 3.2 and 3.3.
3.2. Derivation of the Bohm criterion in the electron sheath
In section 2,the influence of electron-entering velocity on the electron sheath solution has been illustrated, where the inclusion of electron fluid velocityue0as a boundary condition in the sheath entrance shifts the size and potential distribution of the electron sheath. Judging solely from the sheath side,however,the value ofue0seems arbitrary.In this section, the electron sheath will be matched with the presheath which dictates the choice ofue0. The general Bohm criterion will first be applied in the electron sheath, and then the modified Bohm criterion will be proposed considering a more realistic IVDF. The obtained conclusions will be implemented into the following kinetic modeling of the electron sheath under various conditions.
3.2.1. Fluid derivation of the Bohm criterion in an electron sheath. The common procedure for the derivation of the Bohm criterion for an electron sheath is to calculate the electron and ion density at the sheath edge and apply the general Bohm criterion, which is more universal and applies to both electron and ion sheaths. The general Bohm criterion is frequently used directly and was originally proposed in Riemann’s work[30].However,sometimes its exact form can be vague in the literature and may cause misunderstanding when applied to ion and electron sheaths. Here the general Bohm criterion is briefly reviewed and then directly applied to the case of an electron sheath.
Starting from the Poisson equation and expanding it at the sheath edge:



It is noted that in a presheath the quasi-neutrality is satisfied so the electron and ion densities are bothn.
Since the gradient terms become much larger near the sheath edge, it is assumed thatS= 0 andueis solved by using∣M∣=0 in order to get a nontrivial set of solutions,giving the following expression:


3.3. Application of the Bohm criterion in a kinetic model of an electron sheath
3.3.1.Influence of a truncated EVDF on the kinetic model of an electron sheath. In section 3.2, the electron-entering velocityue0is derived with various types of assumption. It is then possible to apply the obtainedue0to revise the EVDF at the sheath entrance. Note that, in section 3.1, the EVDF at the sheath edge is in Maxwellian form and no drift velocity is considered. Whenue0is included, however, the EVDF at the sheath edge is inevitably truncated,and a drift velocity should be included.
For simplicity, the original EVDF is assumed to be a half-Maxwellian with no drift velocity,and then a nonzeroue0is added to see its influence. The comparison of the EVDFs with and without entering velocity is given in figure 6.

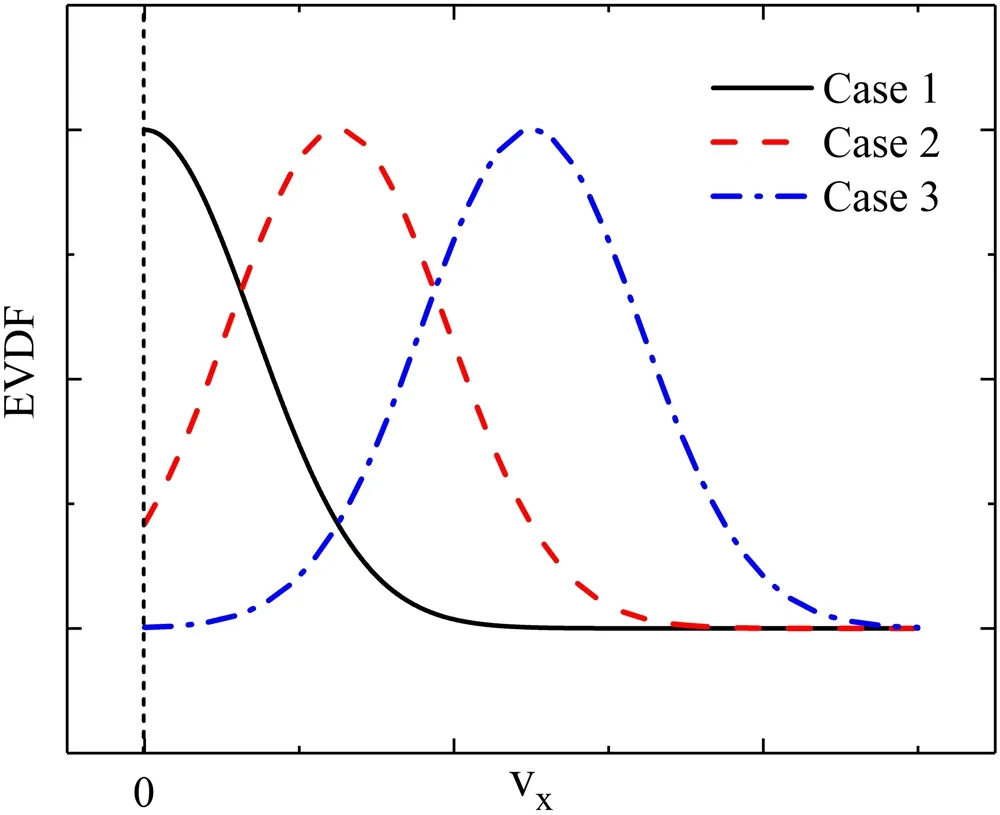
Figure 6.Schematic of the EVDFs with zero or nonzero entering velocity. EVDFs are normalized with respect to the density. Case 1 is the half-Maxwellian case, case 2 is an arbitrary nonzero entering velocity case, while case 3 is similar to case 2 except that the drift velocity is sufficiently large so that EVDF is close to a drifting Maxwellian.

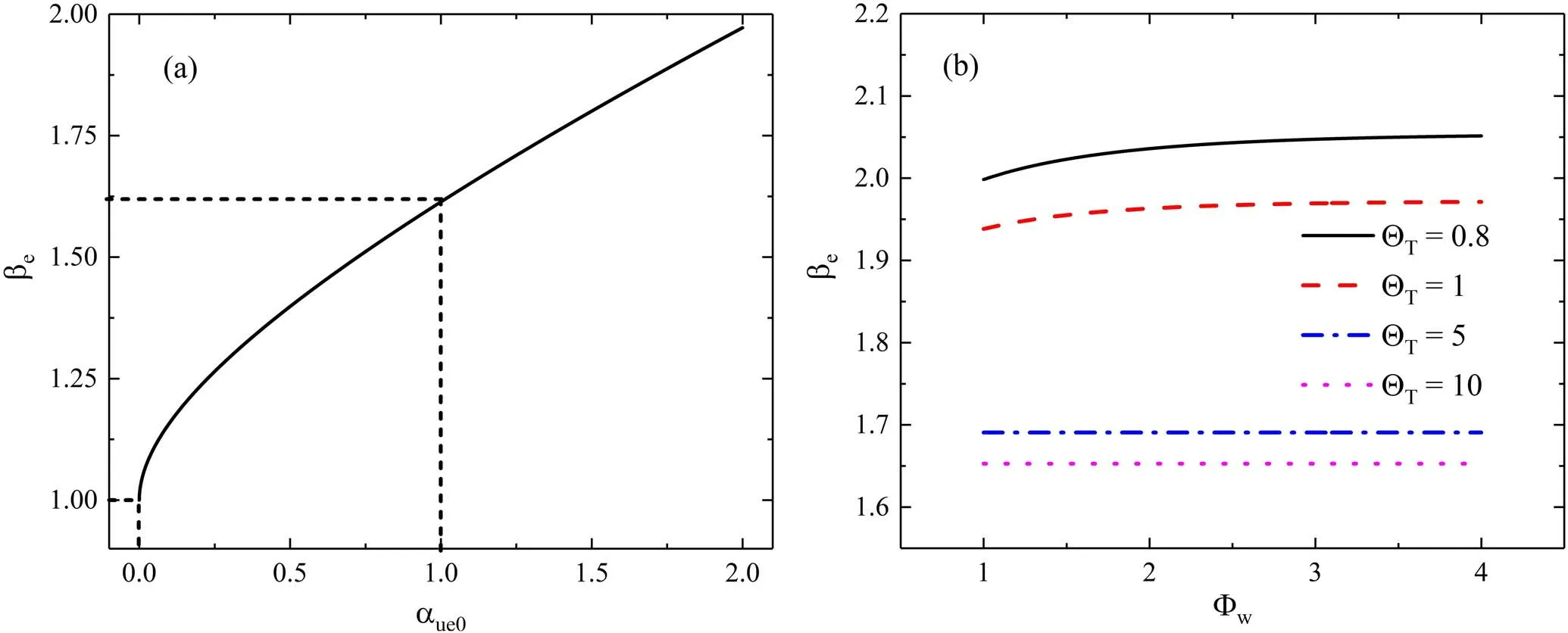
Figure 7. Calculated βe as a function of (a)αue0 and (b)Φw andΘ T.
3.3.2. An attempt to include the Bohm criterion in the kinetic model of an electron sheath. In section 3.1, a kinetic model is established for an electron sheath involving the corrected EVDF at the sheath edge, which provides a numerical solution of the sheath structure. However, the electronentering velocity is not counted in that model. It is therefore intuitive to consider if it is possible to modify the form of EVDF at the sheath edge according to the revised electron Bohm criterion and apply similar methods to further improve the kinetic modeling.It will be shown in the following section that this is not as straightforward as anticipated,and not even can a numerical solution be obtained when the entering velocity is considered.

Figure 8.Schematic of two cases of EVDF and the influence of the relation between ue0 and ve cut .The solid line marks the physical velocity distribution function.

However, when bringing the electron density expression into the Poisson equation, no analytical expression can be obtained from the integral of equations (41) and (42), so not even the numerical solutions of the electron sheath, as in section 3.1, are derivable. This indicates that a compromise has to be made when choosing the electron sheath model:either the electron sheath Bohm criterion is counted and the fluid model is employed (section 2.2) or the kinetic effects(EVDF) are considered while dropping the entering velocity.Future works are expected to propose better solutions and self-consistently combine the truncated EVDF and electron sheath solution.
4. Electron sheath modeling considering the plasma-surface interaction
SEE widely exists in a multitude of scenarios where plasma flux coming from a sheath comes into contact with a solid boundary [31, 33, 34, 39, 40]. Both incident ions and electrons can induce SEE at a solid boundary. The former is generally through Auger neutralization or de-excitation where an ion approaching a solid boundary bends the local field nearby so that the trapped electrons can escape from the solid material [41]. The latter happens when the incident primary electron is de-accelerated after penetrating the material surface while transferring energy to surrounding electrons,some of which could evacuate from the material surface and become true secondary electrons [42].
In low-temperature plasma applications, both types of SEE could happen, but the occurrence of both of them simultaneously is not considered in most if not all plasma simulations. The ion-induced SEE coefficient is independent of the incident ion temperature (only true for cold ion)and is a constant once the wall material is fixed. Recent theories showed that the accumulated surface charges in dielectric materials can modify the ion-induced SEE coefficient [43].The present study focuses on a metallic boundary, hence the ion-induced SEE coefficient remains constant. On the other hand, the electron-induced SEE depends on primary electron energy. The ion-induced SEE is usually counted if the electron temperature is low and the wall material is metallic,which has a lower electron-induced SEE coefficient. Taking the example of plasma processing using capacitively coupled plasma,it is usually the ion-induced SEE that is counted since electrodes are typically metallic and the electron temperature is low [44], whereas the electron-induced SEE was shown to be influential if the neutral pressure is low and the electrodes are made of a more emissive material such as SiO2[45].



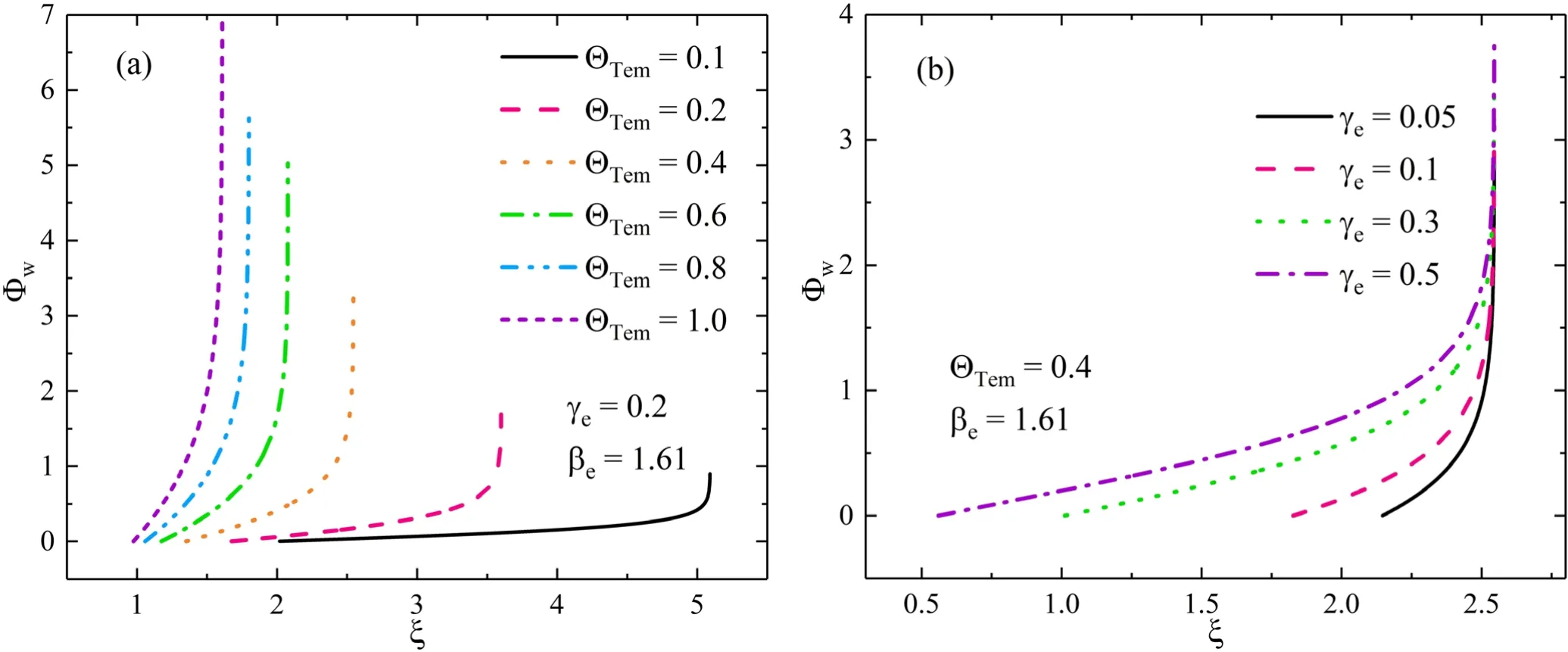
Figure 9.Calculated normalized electrode potential as function ofξ, γe,ΘTem and β e.
The Poisson equation is then:
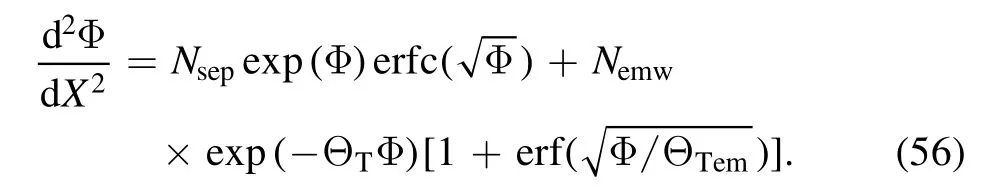
It is, however, not easy to solve equation (56) directly due to the complex integrand.Further study will be performed to calculate the approximate spatial potential profile.
However, the factorγeis not arbitrarily chosen. For thermionic emission or photoemission,theγecan be regarded as constant as long as the electrode temperature or light source remains stable [48, 49], but the present research focuses on SEE where the emission coefficient is energydependent, and therefore closely linked with plasma properties. More precisely, the emission coefficient should be further expressed as:

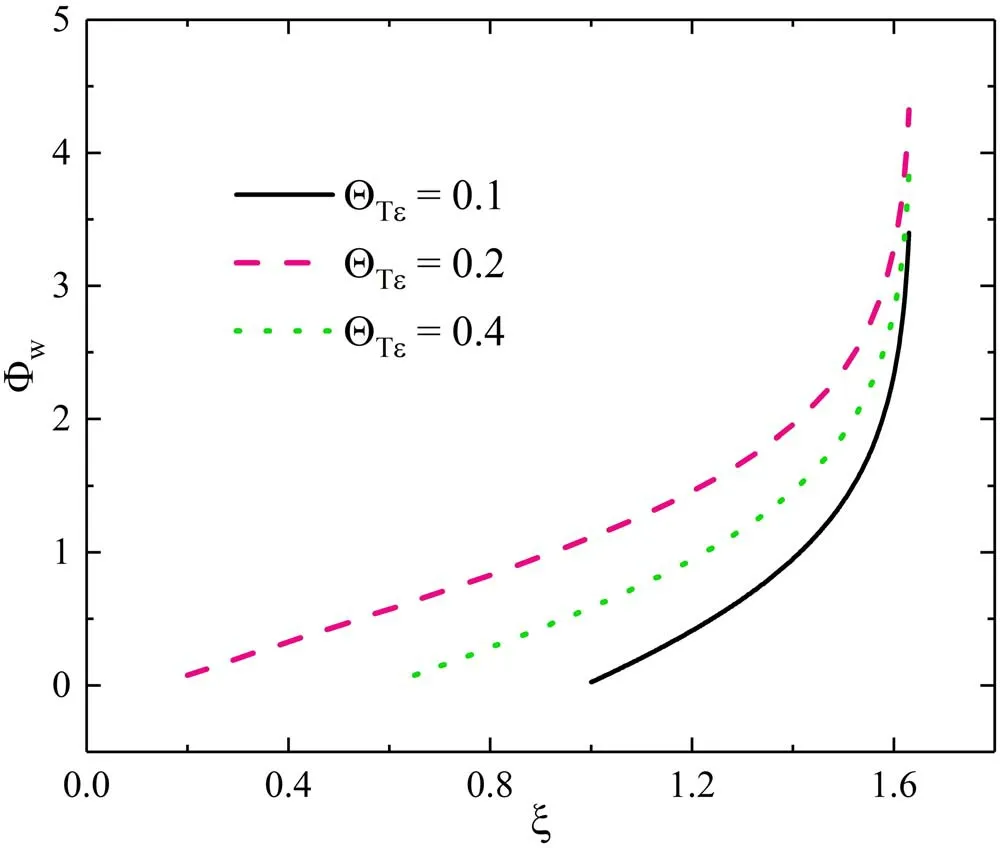
Figure 10.Calculated Φw considering the energy-dependent SEE coefficient.

whereγe,Ris the electron-emission coefficient involving electron reflection. This is because when a reflection occurs,the ‘effective’ SEE coefficient is 1, and if the true SEE happens,the corresponding contribution to the SEE coefficient is the non-reflection probability multiplied by the true SEE coefficient. However, the nature of such a process is not as simple as described here and the coefficientRfis also energydependent [56].
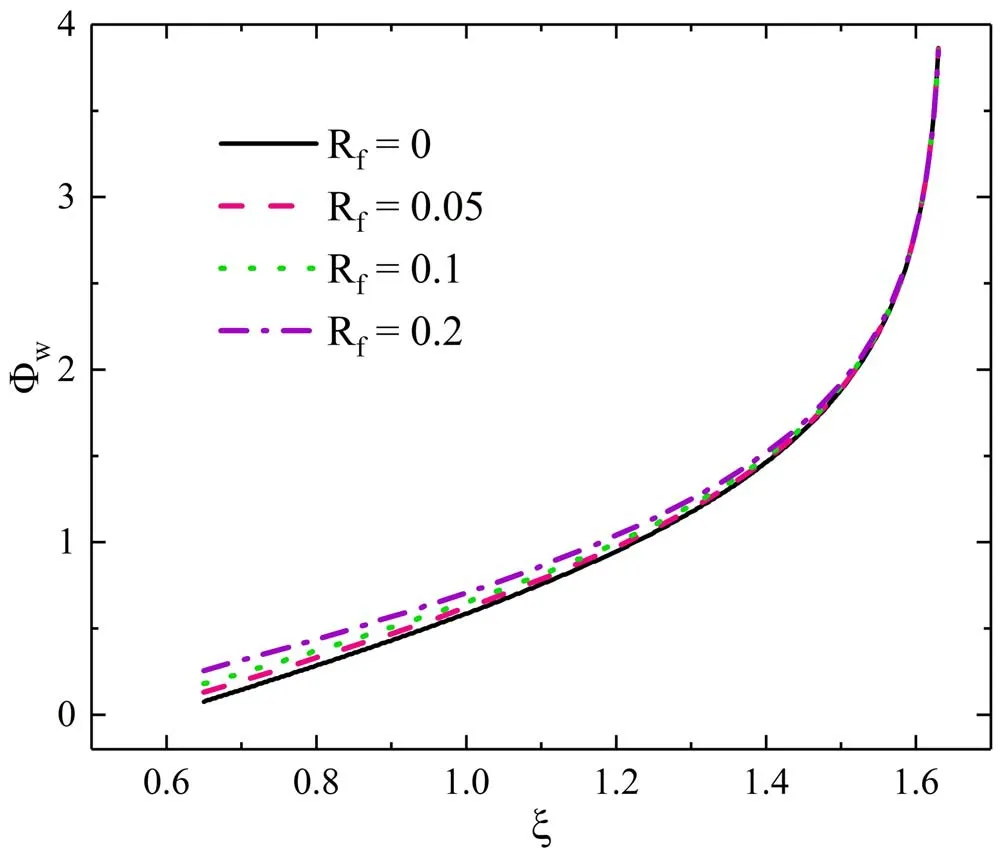
Figure 11.Calculated Φw considering the energy-dependent SEE coefficient and the backscattering. The factorΘ Tε =0.2.


It is worth mentioning that the model derived above is not promptly applicable in strongly magnetized plasmas, e.g.the discharge plasma in a tokamak [48]. Firstly, the electronemission mechanism from plasma-facing components(PFCs)is more complex. Apart from SEE and the backscattering mentioned here, thermionic emission from hot PFCs and transient field emission during edge localized mode are also important. Additionally, the prompt re-decomposition of emitted electrons during initial electron gyration is crucial,which depends on the sheath electric field near the surfaces.The application of the proposed work in such plasma conditions therefore requires more detailed investigations.
Last but not least, the influence of SEE on the electron sheath can be verified experimentally by using different types of electrode (thus differentγe) biased at the same electrode potential, then checking the electron sheath properties posed by different SEE coefficients of the electrodes. Future experimental works are expected to corroborate the theoretical predictions.
5. Conclusions
The present work is dedicated to an improved understanding of electron sheath theory and its implications in plasma-surface interaction using both fluid and kinetic approaches. A fluid model considering the electron sheath entering velocity is proposed and compared to the classic electron sheath Child-Langmuir model. It is shown that the revised fluid model avoids the singularity at the sheath edge in the Child-Langmuir model and the latter tends to overestimate the electron sheath potential. Subsequently, a kinetic electron sheath model is constructed. Nonzero ion temperature is considered while disregarding the electron presheath structure. The kinetic model is shown to predict a higher sheath potential, and the sheath size is reduced with higher ion temperatures. Electron presheath-sheath matching is developed extensively, utilizing a more realistic truncated ion distribution function due to the loss of the cone effect. The electron-entering velocity at the sheath edge is shown to be dependent on electron-ion temperature ratio and the electron sheath potential, implying a change of probe current prediction in the electron saturation region. Electron-entering velocity is higher than the Bohm criterion prediction when a truncated IVDF is employed. Meanwhile, attempts are made to further include the electron-entering velocity into kinetic models. The exact relation between density and potential is obtained while no analytic or numerical sheath potential solution can be derived,revealing a trade-off between electron presheath structure and kinetic treatment of electron sheath. The electron sheath theory is further generalized to include the SEE on the electrode induced by sheath-accelerated plasma electrons. The I-V trace of applied electrode bias potential and electrode current is obtained, influenced by the boundary emission coefficient. Both constant and energy-dependent electron-emission coefficients are employed in the derivation,and the influence of backscattering is discussed. Further insights are also provided for future verifications of the proposed theories.
Acknowledgments
The research was conducted under the auspices of National Natural Science Foundation of China (Nos. 51827809,52077169) and the National Key R&D Program of China(No. 2020YFC2201100).
Appendix
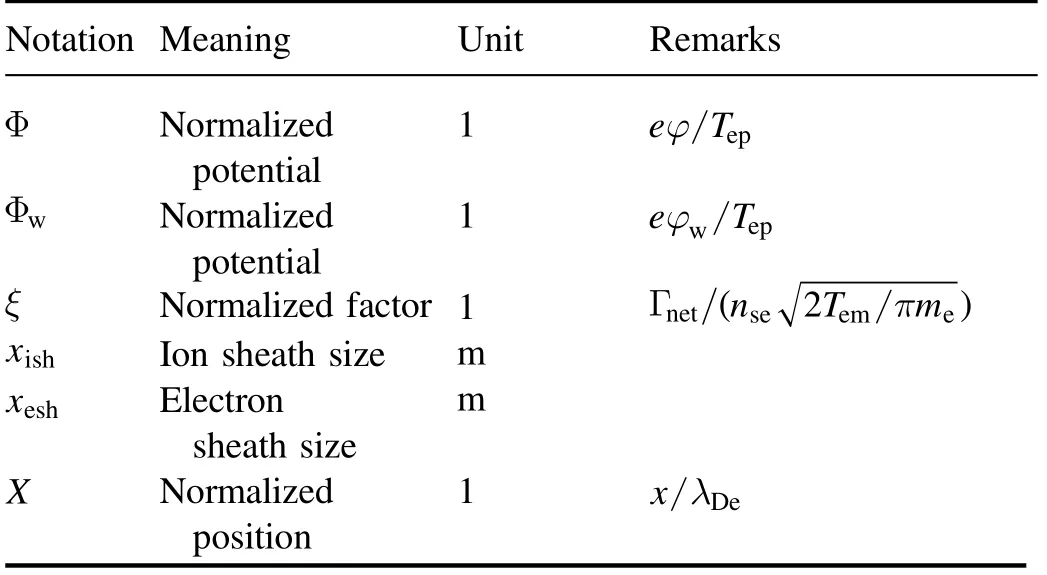
The following table gives the key variables adopted in derivations.

Notation MeaningUnitRemarks αue0Normalized factor 1u=αv e0ue0 the βeNormalized factor 1β Γ= Γ ep,ue0e ep,hM γeSEE coefficient1Γ /Γ emep γe,RSEE coefficient1Consider reflection AcArea of chamber wall m 2Ion sheath presents AwArea of biased electrode-m 2Electron sheath presents ΓepPlasma electron flux-m 2s1 Γep,hMPlasma electron flux- -m 2s1Integrated with fe,hM Γep,ue0Plasma electron flux- -m 2s1Integrated with fe,ue0 ΓiIon flux--m 2s1 ΓnetNet plasma flux--- -m 2s1 ΓerefReflected electron flux m 2s1 ΓemEmitted electron flux- -m 2s1 ε0Vacuum permittivity- -C V 1m1 εseeSEE model factor eV fe,hMHalf-Maxwellian EVDF--m 4s fe,ue0Truncated EVDFm 4s fiIVDF--m 4s EElectric field-V m 1 hiPresheath density drop 1 heVirtual anode density drop 1 ηNormalized potential 1 eT()φ-φ /w i ηseNormalized potential 1 η at sheath edge, eφ /T wi ΘTTemperature ratio 1T/ T epi ΘTemTemperature ratio 1T/ T emep Θ ε TTemperature-1 Tepsee /ε energy ratio

(Continued.)
(Continued.)
ORCID iDs
Guangyu SUN (孫光宇) https://orcid.org/0000-0001-6761-6019
Shu ZHANG (張舒) https://orcid.org/0000-0001-9366-7426
Anbang SUN (孫安邦) https://orcid.org/0000-0003-1918-3110 Guanjun ZHANG (張冠軍) https://orcid.org/0000-0003-1859-0443
 Plasma Science and Technology2022年9期
Plasma Science and Technology2022年9期
- Plasma Science and Technology的其它文章
- Implementation and application of PyNE sub-voxel R2S for shutdown dose rate analysis
- Microchannel cooling technique for dissipating high heat flux on W/Cu flat-type mock-up for EAST divertor
- Development of the pellet injection system on the J-TEXT tokamak
- Degradation of tiamulin by a packed bed dielectric barrier plasma combined with TiO2 catalyst
- Experimental study on surface arc plasma actuation-based hypersonic boundary layer transition flow control
- Efficient direction-independent fog harvesting using a corona discharge device with a multi-electrode structure
