Nonexistence and Existence of Global Solutions for Naghdi's Shell Equation with Nonlinear Damping and Source Terms

CHAI Shugen

(School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China)

Abstract:We consider nonexistence and existence of global solutions for Naghdi's shell equation with nonlinear damping and source terms.Under some assumptions on the damping,source terms and the initial energy,the results of global nonexistence and existence of solutions are presented.

Key words:Naghdi's shell model;global nonexistence;global existence;energy of system

1 Introduction and main results

In this paper,we are concerned with the global existence and nonexistence of solutions for Naghdi's shell equations with nonlinear damping and source terms.This problem has been studied for wave equations and plate equations by many authors;see Levine[1-2],Georgiev and Todorova[3],Aassila and Guesmia[4],Messaoudi[5],Chen and Zhou[6],Antontsev et al[7]and many others.This problem has also been studied for high-order hyperbolic equations;see Zhou et al[8]and Li[9].For thin shell equations,we know little about this problem.

Here we study Naghdi's shell model[10]in the version of Yao[11]where to view the middle surface as a Riemannian manifold with the induced metric inR3.This idea was introduced by Yao[12]to study the exact controllability for the wave equations with variable coefficients and was extended late for other problems in references[13-17,11,18-20].For more,we refer to Yao's book[21].

Here we mainly consider the global nonexistence and existence of solutions in some function spaces for the shell equation.It is shown that the solution is global in time under some conditions without the relation between damping and sources and global solution decays.Furthermore,under some assumptions on the damping,sources and the initial energy,the global nonexistence of solution is proved.

Before stating the main results in Subsection 1.3,we need some preliminary knowledge from Rieman‐nian geometry which is presented in Subsection 1.1.A simple introduction of modeling of Naghdi's shell equation is introduced in Subsection 1.2.

1.1 Some notations in Riemannian geometry

Let us first introduce some notations from Riemannian geometry.It is noted that all these definitions and notations are standard and classical in literature.

Denote bythe usual dot inner product ofR3.LetMbe a surface ofR3,which is assumed to be smooth for simplicity.In the natural way,Mproduces a Riemannian manifold of dimension two with the in‐duced metric ofR3that is denoted bygor simply by.For eachx∈M,Mxrepresents the tangential space ofMatx.It is assumed thatMis orientable in terms of the unit normal fieldNonM.The set of all vector fields onMis denoted byX(M).The set of allk-order tensor fields and the set of allk-forms onM are denoted byTk(M)andΛk(M),respectively,wherekis a nonnegative integer.Then

1.2 Naghdi's shell equation

Let us turn to geometrical displacement equation of Naghdi's shell model developed in[11].Suppose that the middle surface of the shell occupies a bounded regionΩof surfaceMinR3with the normal fieldN.The shell,now a body inR3,is defined by

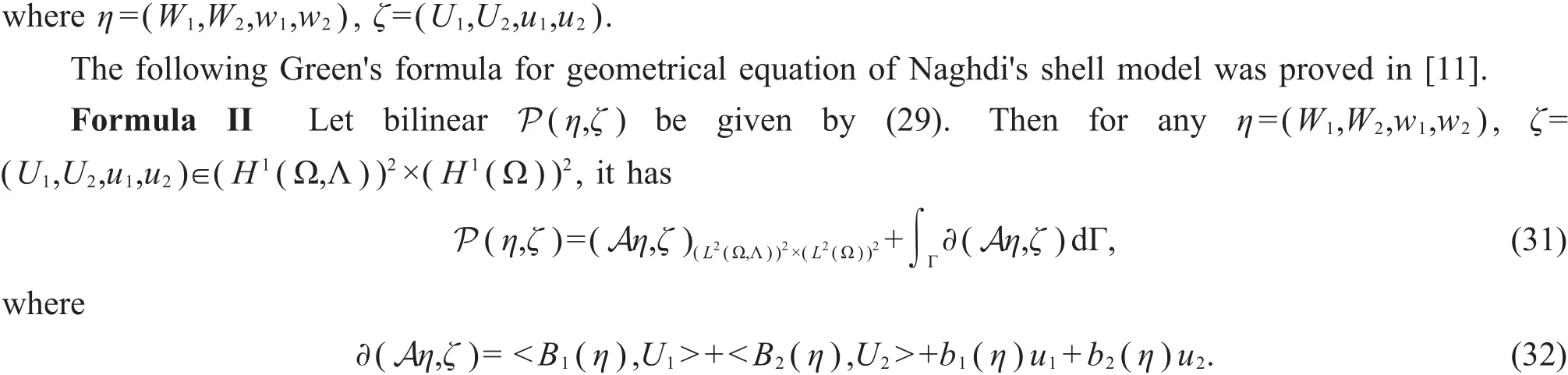
1.3 Model and main results

Theorem 1 (Nonexistence of global solutions).Suppose that theoremq>pand(η0,η1)∈V×H.If one of the followings is satisfied:

(i)E(0)<0;

(ii)0≤E(0),

then the solutionη∈XTto the system(33)cannot exist globally.

Remark 1 In the case ofE(0)<0,the initial potential energy of the system is negative.

Theorem 2 (Global existence and energy decay).Suppose that(η0,η1)∈V×H,P(η0,η0)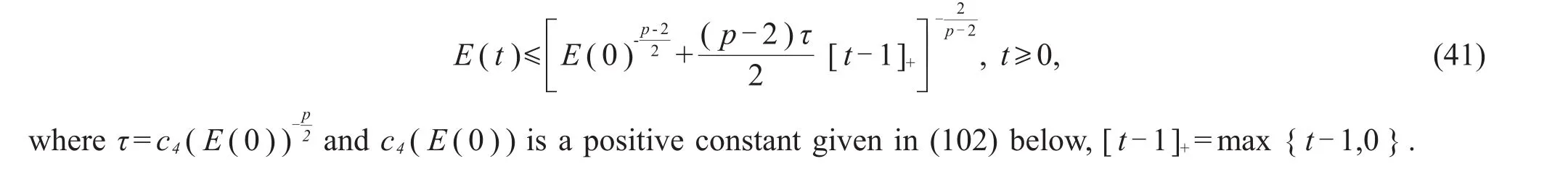

2 Preliminary

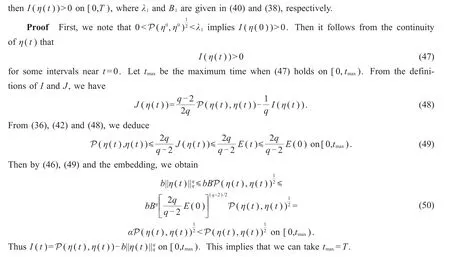
3 Nonexistence of global solutions

4 Global existence and energy decay