矩形的特殊性,動(dòng)點(diǎn)的不變性

廣東省佛山市南海區(qū)里水鎮(zhèn)和順第一初級(jí)中學(xué)(528241) 陳有奮

1 題目呈現(xiàn)

如圖1,在矩形ABCD中,AB=3,AD=4,P是AD上不與A和D重合的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)P分別作AC和BD的垂線,垂足為E,F.求PE+PF的值.

圖1

本題來(lái)源于北師大版義務(wù)教育教科書九年級(jí)上冊(cè)第一章“特殊平行四邊形”第二節(jié)第三課時(shí)的課后練習(xí)題5.

2 教學(xué)價(jià)值

矩形的第三節(jié)課,是一節(jié)綜合了性質(zhì)與判定的練習(xí)課,而這一道題目側(cè)重鞏固矩形的特殊性質(zhì):對(duì)角線相等,同時(shí),融入了動(dòng)態(tài)的問(wèn)題.在動(dòng)態(tài)的過(guò)程中,需要學(xué)生抽象出本質(zhì)的東西,找到變化中的不變量,再證明求解,培養(yǎng)邏輯推理能力.在矩形為背景的幾何圖形中,尋找求線段和的基本圖形,培養(yǎng)幾何直觀素養(yǎng).

3 功能分析

本題的其中一個(gè)條件是四邊形ABCD是矩形,如何根據(jù)條件與結(jié)論找到矩形作用于本題的有效性質(zhì),是解決這道題目的關(guān)鍵因素之一,所以這道題目提供了特殊平行四邊形性質(zhì)運(yùn)用的范例,也為如何抽取有效信息提供參考.

近年來(lái),許多地方中考的壓軸題都出現(xiàn)“動(dòng)態(tài)問(wèn)題”.學(xué)生對(duì)于動(dòng)點(diǎn)問(wèn)題,心理上存在畏懼.這需要平時(shí)教學(xué)循序漸進(jìn)地進(jìn)行動(dòng)點(diǎn)問(wèn)題的練習(xí).而本題不存在多種情況的分類,適合學(xué)生建立動(dòng)點(diǎn)問(wèn)題的信心,建立“以靜制動(dòng)”的意識(shí).

本題中所求線段為PE,PF都是垂線段,并且求PE+PF的值,這些都是幾何題常見的問(wèn)題:垂線段的用法,線段求和問(wèn)題.通過(guò)本題,歸納出相關(guān)的方法.

4 教學(xué)措施——課堂呈現(xiàn)

4.1 給予充分的時(shí)間

這是一節(jié)練習(xí)課課后習(xí)題,由于題目具有較強(qiáng)的綜合性,需要在課堂解決.對(duì)于能力強(qiáng)的學(xué)生應(yīng)給出充足獨(dú)立思考思想,老師不應(yīng)該過(guò)多的干預(yù),而對(duì)于數(shù)學(xué)基礎(chǔ)較弱的學(xué)生應(yīng)給予一定的幫助引導(dǎo),讓不同的層次的學(xué)生得到不同的發(fā)展.對(duì)于暫時(shí)找不到方法的同學(xué),設(shè)計(jì)如下問(wèn)題:

問(wèn)題1.過(guò)點(diǎn)P分別作AC和BD的垂線這個(gè)條件應(yīng)與題目的另一條件“矩形ABCD”怎么結(jié)合運(yùn)用?

(關(guān)注矩形的對(duì)角線相等平分的性質(zhì),即OA=OD.)

問(wèn)題2.條件中的垂直應(yīng)如何應(yīng)用? 垂直有哪些用法?

問(wèn)題3.P點(diǎn)在運(yùn)動(dòng),所求的兩線段長(zhǎng)度在變化,那么所求的和會(huì)變嗎?

4.2 展示解題過(guò)程

課堂上各抒己見,百花齊放.同時(shí)要避免學(xué)生平鋪直敘的分享自己的方法,不能引起其他學(xué)生的共鳴,所以要根據(jù)學(xué)生的方法適當(dāng)?shù)脑O(shè)計(jì)問(wèn)題,引起大家的思考,從中體會(huì)不同的解題方法.

4.2.1 特殊值法

當(dāng)P運(yùn)動(dòng)到AD的中點(diǎn)時(shí),線段PE與PF的長(zhǎng)度確定下來(lái),并且兩線段相等.然后可設(shè)AE為x,根據(jù)RtΔAPE和RtΔAOE勾股定理,以PE為等量關(guān)系建立方程.或者運(yùn)用等面積法求得AE.

這種方法雖然不具有一般性,局限于選擇填空題,但是動(dòng)點(diǎn)問(wèn)題,選擇某個(gè)特殊的瞬間,這是以靜制動(dòng)的入門.

4.2.2 等面積法

由于本題不存在多種情況,所以我們可以選擇P點(diǎn)在某一位置時(shí),用靜態(tài)的具體的圖形研究問(wèn)題,抽象出動(dòng)態(tài)中的不變量.

運(yùn)動(dòng)過(guò)程中,矩形的相關(guān)的量是不變的,PE始終垂直于AC,PF垂直于BD(位置上的不變).當(dāng)思路不明朗時(shí),回憶垂直的用法(圖2),通過(guò)排除,選擇用等面積法.

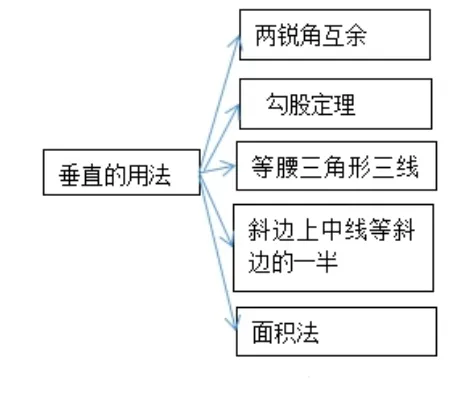
圖2

PE是哪個(gè)三角形的高呢? (ΔAEP,ΔAOP,ΔACP)選擇哪個(gè)三角形呢?

目的:通過(guò)設(shè)計(jì)問(wèn)題,讓學(xué)生思考解決問(wèn)題的突破口.

ΔAEP的底邊AE隨著P的變化也在變化而另外兩個(gè)三角形的底邊AO,AC都沒(méi)有變化,同時(shí)考慮另一以PF為高的三角形面積,ΔAPC和ΔBPD的面積,兩者建立不了聯(lián)系.所以選擇用ΔAOP的面積建立PE的關(guān)系.

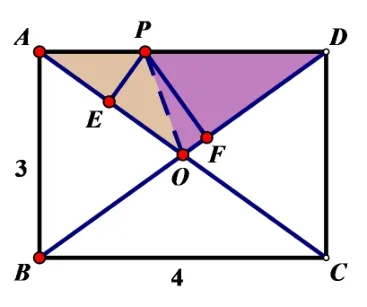
圖3

本題在矩形的背景中運(yùn)動(dòng),抽象出運(yùn)動(dòng)中垂直這一位置的不變性,聯(lián)想到高,運(yùn)用面積問(wèn)題,發(fā)現(xiàn)兩三角形面積相加為定值,根據(jù)對(duì)同一圖形面積算二次的等面積法進(jìn)行代數(shù)運(yùn)算,由矩形的性質(zhì)推導(dǎo)的OA=OB是出現(xiàn)PE+FF的關(guān)鍵,從而求得兩線段之和.

4.2.3 極值法

生:根據(jù)求PE+PF的值,所以兩線段之和為定值.把P無(wú)限的接近D點(diǎn)(圖4),發(fā)現(xiàn)PF無(wú)限接近零,而PE的長(zhǎng)度接近D到AC的距離.所以PE+PF的值為DE的長(zhǎng)度.

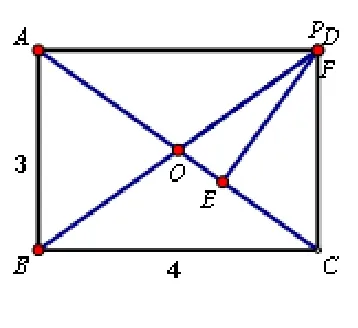
圖4

對(duì)于初中學(xué)生而言,極值法比較抽象,難以理解.

師:怎么說(shuō)明PE+PF就是D到AC的距離? 證明線段和等于有某一線段有哪些方法?

生:截長(zhǎng)補(bǔ)短法.

給與學(xué)生思考新的求法.

4.2.4 截長(zhǎng)法

生:過(guò)D作DI⊥AC,過(guò)P作PJ⊥DI(圖5),根據(jù)三個(gè)角是直角的四邊形是矩形,判定四邊形PEIJ是矩形,所以PE=JI,相當(dāng)于在DI上截取IJ=PE.只要證明DJ=PF即可.通過(guò)證明ΔPFE∽=ΔDJP.其中PD=PD,∠PFD=∠PJD=90°,根據(jù)PJ//EI,所以∠2=∠3,而OA=OD,所以∠1=∠3,所以∠1=∠2,全等可證.所以PE=JI,DI的長(zhǎng)度為PE+PF的值.

圖5

師:P點(diǎn)在運(yùn)動(dòng),始終有這個(gè)結(jié)論嗎?

這個(gè)問(wèn)題的提出是讓學(xué)生再次感受以靜制動(dòng)是解決動(dòng)點(diǎn)問(wèn)題的關(guān)鍵.無(wú)論P(yáng)運(yùn)動(dòng)在哪里,可以進(jìn)行上述操作,矩形ABCD是不動(dòng)的,矩形PEJI雖然在運(yùn)動(dòng),卻始終是矩形,PJ//EI是不變的關(guān)系,所以動(dòng)態(tài)的PF=DJ.

4.2.5 補(bǔ)短法

生:延長(zhǎng)EP到I使得PI=PF(圖6),所以PE+PF就轉(zhuǎn)化成PE+PI,也就是求IE的長(zhǎng)度.連接ID.

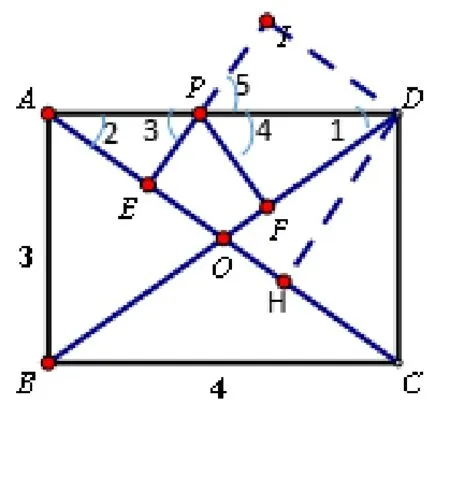
圖6

師:為何想到連接ID.

生:因?yàn)檠娱L(zhǎng)PE后,我覺得是把ΔPFD通過(guò)AD對(duì)稱到ΔPID,所以就連接DI,然后聯(lián)想到∠I是直角.也就是所求的線段IE是ID,AC兩平行線間的距離.過(guò)D作DH⊥AC,也產(chǎn)生了一個(gè)矩形IEHD,求IE的長(zhǎng)度就是求DH的長(zhǎng)度.

學(xué)生通過(guò)把PE進(jìn)行補(bǔ)短法,把PE,PF放在同一線上,整個(gè)思維過(guò)程是一種直覺思維為主,如“感覺把ΔPFD通過(guò)AD對(duì)稱到ΔPID,也就是要證明這兩個(gè)三角形全等.我們還需進(jìn)行邏輯推理.

由于OA=OD,∠1=∠2,ΔAPE和ΔPDF都是直角三角形,所以∠4=∠3,而∠3=∠5,從而∠4=∠5,PD=PD,PF=PI,所以ΔPFD∽=ΔPID,可得∠I是直角.

此方法是補(bǔ)短法,一開始,目標(biāo)就很明確,而學(xué)生的“圖形感”——圖形的對(duì)稱性,構(gòu)造矩形等,這一系列的直覺思維為證明指出了方向,再根據(jù)矩形的性質(zhì)進(jìn)行嚴(yán)謹(jǐn)?shù)倪壿嬐评?兩種思維交替進(jìn)行,這往往是解決綜合性幾何題常用的手段.

4.2.6 函數(shù)思想

4.3 各種方法小結(jié)

知識(shí)層面,上述的4 中方法,都用到了矩形的對(duì)角線相等的性質(zhì).這是有題目本身的條件所決.

方法層面,在動(dòng)態(tài)中需要抽象出不變的量,絕對(duì)靜態(tài)的不變量是矩形ABCD及其相關(guān)聯(lián)的量,相對(duì)不變的量有PE⊥AO,PF⊥BO,以及在運(yùn)動(dòng)過(guò)程中,某一動(dòng)態(tài)的線段或者角度始終跟另一量相等,從而建立數(shù)量關(guān)系.所以動(dòng)態(tài)的題目需要“以靜制動(dòng)”,找到某個(gè)瞬間作為解題的圖形,把問(wèn)題轉(zhuǎn)化為普通的幾何題.

求線段的長(zhǎng)度或者是求線段和的問(wèn)題,本習(xí)題運(yùn)用了等面積法,截長(zhǎng)法,補(bǔ)短法等典型的方法,解題后的反思應(yīng)從方法層面進(jìn)行小結(jié),讓學(xué)生能夠通過(guò)一道題目,衍生出多種解決問(wèn)題的方法,實(shí)現(xiàn)以小勝多.本題是以矩形背景的動(dòng)點(diǎn)題目,通過(guò)最后的結(jié)論,發(fā)現(xiàn)所求是一個(gè)定值,而整個(gè)運(yùn)動(dòng)并非圍繞整個(gè)矩形展開,所以可讓學(xué)生歸納出一般性的結(jié)論:等腰三角形的邊上的一點(diǎn),到兩腰的距離之和為一定值,這一定值等于一腰上的高.

由抽象的動(dòng)點(diǎn)問(wèn)題到某個(gè)瞬間的靜態(tài)幾何圖形,再由具體到一般的歸納,使整道題目上升到一個(gè)結(jié)論的高度,培養(yǎng)學(xué)生的抽象能力,語(yǔ)言表達(dá)能力,使學(xué)生透過(guò)運(yùn)動(dòng)的表象看到了本質(zhì)屬性.

4.4 以變促鞏固

如圖7,在矩形ABCD中,已知AD=4,AB=3,點(diǎn)P是射線AD上的一點(diǎn),當(dāng)P經(jīng)過(guò)點(diǎn)D后,PE⊥AC,PF⊥BD,E,F分別是垂足,求PE-PF的值.

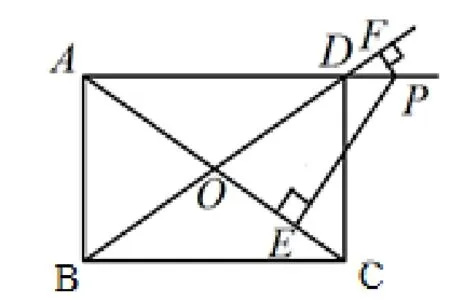
圖7

此變式既源于本題又高于本題,上述的所歸納的知識(shí)層面和方法層面,都可以在變式題中再次運(yùn)用.同時(shí)變式題的構(gòu)圖比原題稍復(fù)雜,原題是“加法”(面積和,線段和),變式是“減法”.不是一味地照搬,而是把原題的方法進(jìn)行遷移,培養(yǎng)學(xué)生靈活運(yùn)用知識(shí)與方法.

5 教學(xué)反思

通過(guò)題目的條件以及圖形的位置關(guān)系,結(jié)合特殊圖形(如本題的矩形)的性質(zhì),能迅速聯(lián)想到其所需的性質(zhì),這正是思維敏捷性的體現(xiàn),并與題目相關(guān)條件進(jìn)行有機(jī)結(jié)合,這是提高解題能力的關(guān)鍵.

本題通過(guò)一題多解,對(duì)于求線段和的問(wèn)題,建立不同的方法,通過(guò)條件的不同的組合建立起與結(jié)論的關(guān)系,這個(gè)過(guò)程就是推理的不同表現(xiàn)形式,有利于學(xué)生通過(guò)同一知識(shí)的不同求法建立這一問(wèn)題的知識(shí)體系,提高學(xué)生的推理能力.

從不用的方法中,體現(xiàn)了同一知識(shí)間的相互轉(zhuǎn)化,如本題中的動(dòng)點(diǎn)問(wèn)題的處理,雖然方法有所不同,卻是同樣概括運(yùn)動(dòng)中的不變量,歸納出不同方法間的共性,從不同解題方法中培養(yǎng)學(xué)生的概括能力.

學(xué)生能力的提升并非一蹴而就,必須充分發(fā)揮例習(xí)題的功能,而不僅僅是知識(shí)層面上的鞏固,更應(yīng)該從每道題目中都要有所收獲,能力在潛移默化中提升.