Effect of non-Markovianity on synchronization
Kun-Jie Zhou (周坤杰), Jian Zou (鄒健), Bao-Ming Xu (徐寶明),Lei Li (李磊) and Bin Shao (邵彬)
1 School of Physics, Beijing Institute of Technology, Beijing 100081, China
2 Shandong Key Laboratory of Biophysics, Institute of Biophysics, Dezhou University, Dezhou 253023,China
3 School of Physical Science and Technology, Inner Mongolia University, Hohhot 010021, China
Abstract We investigate the transient spontaneous quantum synchronization between two qubits interacting with a common non-Markovian environment based on a collision model.We are mainly interested in the effect of non-Markovianity on the synchronization between two qubits.We find that the non-Markovianity always delay the anti-synchronization and decrease the parameter region where the qubits get anti-synchronized.Meanwhile, we defineV to characterize the visibility of synchronization and show that there is an apparent link amongV, entanglement and quantum mutual information whether in the Markovian or non-Markovian regimes when the environment is in the vacuum state.Moreover, with the increase of temperature, the parameter region of the emergence of anti-synchronization and the time to get anti-synchronized in the non-Markovian regime gradually approaches that in the Markovian regime.The high temperature decreases the parameter region of the emergence of anti-synchronization in both Markovian and non-Markovian regimes, and breaks the connection amongV, entanglement and quantum mutual information.
Keywords: quantum synchronization, non-Markovianity, entanglement, quantum mutual information
1.Introduction
Synchronization is a fundamental phenomenon widely existing in nature [1].The first observation of synchronization could date back to the 17th century [2], and then the theory of synchronization has been developed and perfected by a large number of researchers [3–5].Nevertheless, classical synchronization theory can not accurately describe and analyze the synchronization phenomenon in microscopic system where the quantum effect should be considered.Recently, the synchronization in quantum regime has been studied and attracted considerable attention as reviewed in [6].Synchronization in quantum system can be classified into two types, specifically,synchronization driven by an external field and spontaneous synchronization, which have been investigated in many different systems [7–26].Meanwhile, synchronization shows its importance in many areas, such as quantum communication[27, 28].Recently, the phenomenon of synchronization in quantum domain has been experimentally observed [29, 30].
In previous studies, some focus on the synchronization after the system reaching its steady state [20, 30–32], others concentrate on the transient synchronization which appears in the evolution as it decays to the steady state [17–20, 33–41].Recently, several studies have suggested that there is an apparent link between the temporal correlations and synchronization.It has been proposed that mutual information is a useful order parameter which can capture the emergence of synchronization between two Van der Pol oscillators in both classical and quantum regimes [36].Meanwhile, quantum correlation such as entanglement and quantum discord has been studied for a detuned spin pair in a common environment, and it has also been manifested to be related to the appearance of synchronization [34].Despite an apparent link between the appearance of synchronization and the behavior of correlations in the global system in certain models, there exists no general connection between them.Besides, the relations between synchronization and coherence [15], synchronization and relative entropy [42] have been also investigated in different systems.
Dissipation is a key ingredient for spontaneous synchronization, and different forms of dissipation have been considered in the synchronized dynamics[43].Generally,the spontaneous synchronization was investigated for the Markovian dissipative environment.However, in some cases, the memory effect of environment should be considered, which leads to the non-Markovian dynamics.Recently, more and more attention has been paid to the non-Markovian dynamics of open quantum systems [44–46].Then it is interesting to investigate the spontaneous synchronization in a non-Markovian environment.Unfortunately, little is known about the relationship between quantum spontaneous synchronization and non-Markovianity.To our knowledge,there is so far only two studies in this direction.Karpat et al considered a model of two coupled qubits one of which interacts with a dissipative environment,and found that the non-Markovianity of the qubit indirect coupled to the environment is detrimental for the emergence of synchronization between the two qubits[47].And Zhang et al showed that, for two homogenous subsystems, synchronization can always be synthesized without designing direct Hamiltonian coupling given that the degree of non-Markovianity is below a certain threshold[48].However, the question of how the non-Markovianity affects the spontaneous synchronization in the more general case of two qubits subjected to a common non-Markovian environment has not been considered.In this paper, we fill this gap by considering the transient spontaneous synchronization of two qubits in a common non-Markovian environment.
Generally, the effects of environment on the open quantum system dynamics are incorporated into an effective description in terms of master equation for the reduced density matrix of the system[49,50].While collision models offer an alternative way in simulating the open quantum system dynamics [51–58].Benefit from the highly controllability of collision model,the dynamics of the open quantum system can be investigated in great detail.In the microscopic framework of collision model [59, 60], a non-Markovian dynamics can be obtained by introducing an inner-environment ancilla collision[61].It is noted that the synchronization based on the collision model has been studied recently [47, 62].
In this paper, we investigate the transient spontaneous synchronization of a two-qubit system in a non-Markovian environment based on the collision model.We choose the Pearson correlation coefficient to characterize the degree of synchronization.We find that the non-Markovianity always delays the anti-synchronization, and decreases the parameter region where the subsystems get anti-synchronized.Moreover,we defineV to characterize the visibility of synchronization.Particularly, we find that there is an apparent link amongV,entanglement and quantum mutual information when the environment is in the vacuum state whether in the Markovian or non-Markovian regimes.With the increase of temperature, the parameter region of the emergence of anti-synchronization and the time to get anti-synchronized in the non-Markovian regime gradually approaches that in the Markovian regime.Meanwhile,the high temperature decreases the parameter region of the emergence of anti-synchronization in both Markovian and non-Markovian regimes, and the correspondence among the visibility of synchronization, entanglement and quantum mutual information is broken.
The rest of this paper is organized as follows.In section 2 we introduce the model used in this paper.In section 3 we investigate the effect of non-Markovianity on synchronization in different parameter setting, and explore the relationship among the visibility of synchronization, entanglement and quantum mutual information.Meanwhile, we discuss the effect of environment temperature on synchronization.Finally, in section 4 we give the conclusion.
2.Model
We consider a bipartite system S,consisting of a pair of twolevel subsystems S1and S2with different frequencies ω1and ω2, which are coupled to a common environment E, consisting of a sequence of identical ancillae(E1,E2,...,En).We assume that there is no initial correlation between the two subsystems or the environment ancillae.Within the framework of collision model, we investigate the transient spontaneous synchronization between the two subsystems.The dynamic process is composed of a series repeated steps.In the nth step of the dynamics, S1and S2interact with the same environment ancilla Ensequentially.Then after a free evolution of the whole system S, two adjacent environment ancillae Enand En+1interact with each other.And this process is repeated to the next environment ancilla En+1.In figure 1, the detail of the collision model and the interaction process is shown.

Figure 1.Sketch of a bipartite system S made up of two subsystems S1 and S2 interacting with the environment ancillae sequentially.In the nth step of the dynamics, S1 interacts with En; S2 interacts with En; and followed by a free evolution of the system S; next, two adjacent environment ancillae En and En+1 interact with each other.Then S1 and S2 shift by one site, and this process is repeated to the (n+1)th ancilla.
The free evolution of system S is characterized by the Hamiltonian

The interaction between S1and the nth environment ancilla Enis described by the Hamiltonian



where J characterizes the coupling strength between the subsystem and the environment ancilla En.The corresponding unitary evolution operator is written aswithδts1ncharacterizing the time interval of the coupling between S1and the environment ancilla En.Similarly and the corresponding unitary evolution operator isexpwithδts2ncharacterizing the time interval of the coupling between S2and the environment ancilla En.Then we obtain the total unitary evolution operator of the subsystems S1, S2and the environment ancillaand the corresponding dynamic map of the interaction between the system S and the environment ancilla Encan be written as

Next, we introduce an interaction between two adjacent environment ancillae Enand En+1, and assume that the corresponding unitary evolution operator is

Hereis the SWAP gate,and in the ordered basis{|0〉,|1〉}it reads


When γ=0, there is no information exchange between two adjacent environment ancillae, and the dynamic process is Markovian.Whenthere is a maximal information exchange between two adjacent environment ancillae, so the dynamic process becomes fully non-Markovian.
Furthermore,we retain the nth sub-environment freedom until the system interacts with the(n+1)th sub-environment,i.e.the correlation established after S colliding with En+1is erased only after En+1has collided with En.The dynamic map resulting from this implementation thus gives rise to the reduced state of the system

whereTrn-2[·] denotes the partial trace over the (n-2)th environment ancilla prior to the interaction between S and En-1,andis the density matrix of system and the(n-1)th environment ancilla.Then the initial state of next step of the dynamics can be written as ρs?ρn+1, where ρn+1is the density matrix of a fresh environment unit.
3.Result
In this paper we use the Pearson coefficient[6]to characterize the degree of synchronization between the local observables of the subsystems.Given variables x and y, it can be expressed as

whereandare the mean values of x and y respectively,and n is the number of values the variables can take.C12=0 indicates there is no synchronization between the subsystems;C12=1 indicates synchronization; and C12=-1 indicates anti-synchronization.Without lose of generality,in this paper we choose〈σx〉 = Tr [ρsσx]as the local observable to witness the synchronization between S1and S2.In numerical calculation we can not take the summations in equation(9)over the whole data set and generally take a part of it.To avoid sharp fluctuations of C12, we take the average value of the nearest 140 data points as one value of the Pearson coefficient, and then calculate the next value of the nearest 140 data points with an interval of 15 data points from the first data point of the prior data set, to obtain another value of the Pearson coefficient.In this way, a smooth curve of C12can be obtained [62].
In the following, we investigate the synchronization between S1and S2, and compare the behavior of synchronization in the Markovian regime and non-Markovian regime.We suppose that the initial state of the system isMeanwhile, we assume that the environment ancillae are identical and in the same initial state ρe=|0〉〈0|.From the numerical calculation,we find that the time for the subsystems to get anti-synchronized is different for different parameter region.In the parameter region of small λ and large Δ, even though the Pearson coefficient can eventually approaches -1 with a long enough evolution time, the expectation values of the local observables become extremely small.In other words, the system has reached its steady state before the transient synchronization appears.We argue that in this case even though the Pearson coefficient can arrive at -1 finally, there is no visibility for this anti-synchronization.So in this paper when the Pearson coefficient has not reached -1 before the expectation value of the local observable decays to 10-4of the initial value,we say that the two qubits can not be synchronized.It is worth emphasizing that the magnitude of this value makes no qualitative difference to the following results in this paper.In figure 2(a) we display the behavior of Pearson coefficient between S1and S2in terms of detune Δ and coupling strength between two qubits λ in the Markovian regime (γ=0).Without lose of generality,we suppose that the coupling strength between the subsystems and the environment ancilla J=0.3ω, and ω1=ω.To avoid the situation of extremely small expectation values of local observables, the final collision times we choose N=5000.As expected, we obtain a typical Arnold tongue which is shown in figure 2(a).It can be seen that the two subsystems tend to anti-synchronize in most area of parameter region except for very small values of λ and large values of Δ.Only when the coupling strength between S1and S2is strong enough to compensate the effect of detune, the anti-synchronization appears.When we increase N a little,the blue region in figure 2(a)would increase slightly.While as N increases further we find that although some region (especially the region with small λ and large Δ)turns into blue,i.e.C12~-1, the expectation value of the local observables would be extremely small before that.In this case there is no visibility of the synchronization, and according to our argument we say that it can not get anti-synchronized.From numerical calculation we find that by considering the visibility of synchronization when N >5000, the result makes no qualitative difference from figure 2(a).
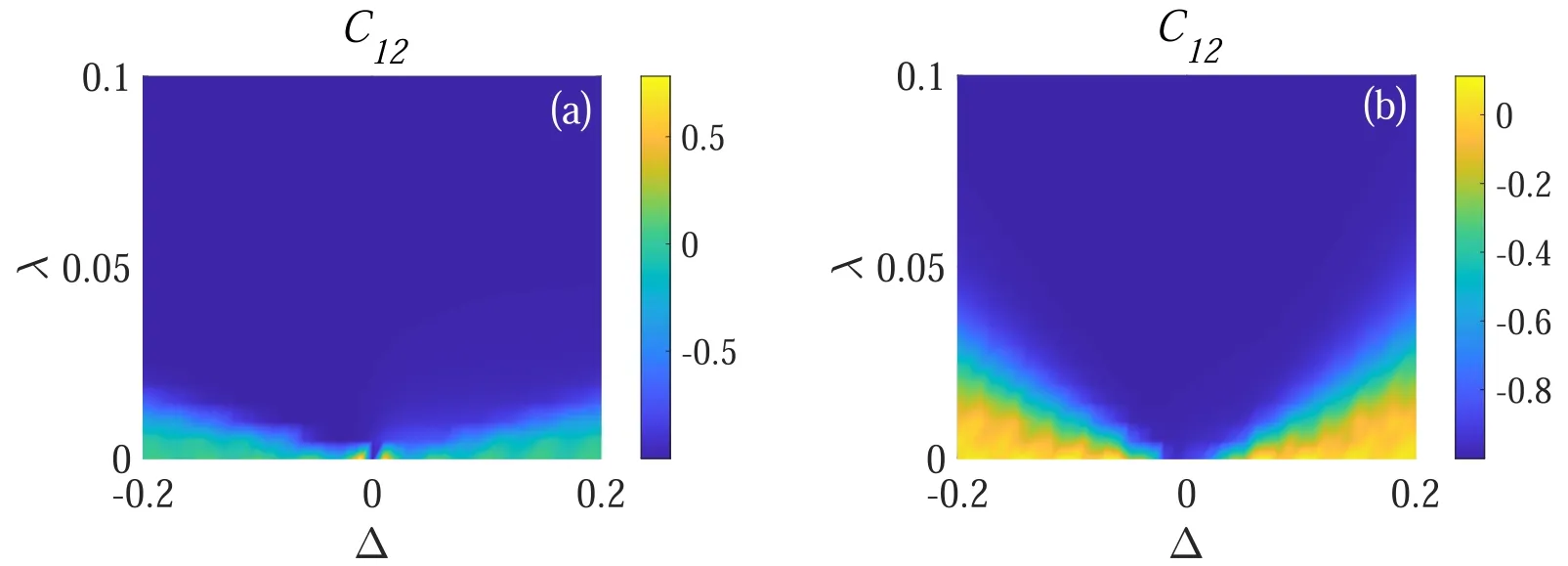
Figure 2.The Pearson coefficient as a function of Δ and λ.For (a) γ=0, and (b)γ = We set J=0.3ω, ω1=ω, N=5000,and ωδt s 1 n = ωδt s 2n = ωδt s 1 s 2 =0.2.
Next,we turn our attention to studying the effect of non-Markovianity on the synchronization between S1and S2by considering a nonzero γ.In figure 2(b),we show the behavior of Pearson coefficient between S1and S2in terms of Δ and λ in the non-Markovian regime.Without lose of generality, we setand the other parameters are the same as in figure 2(a).In the yellow region of figure 2(b), the two subsystems have not gotten anti-synchronized at N=5000.Similar to figure 2(a)as we mentioned above,the blue region would be enlarged for a longer evolution time but by considering the visibility of synchronization the result remains qualitatively unchanged despite the quantitative differences to figure 2(b).Comparing figures 2(a) and (b), we can find that the region of emergence of anti-synchronization is decreased compared with that in the Markovian regime.It is easy to see that the non-Markovianity hinder the emergence of anti-synchronization between the two qubits.
From the above discussion, we argue that the Pearson coefficient can not fully characterize the synchronization between the subsystems.In the parameter region that C12~-1, the amplitude of the expectation value of local observables can well reflect the visibility of synchronization phenomenon as an auxiliary.We define the visibility of synchronizationV as the average absolute value of the expectation value of the local observables

To avoid sharp fluctuation ofV, in the numerical calculation we divide the data points into a series of continuous subsets and each subset contain M data points, then we take the maximum value of each subset as one value ofV.In this paper without lose of generality,we set M=20.In the region that the Pearson coefficient approaches -1, a bigger value ofV characterizes a more apparent anti-synchronization phenomenon.
Next, we tend to investigate the relation among the visibility of synchronization, entanglement and quantum mutual information in both Markovian and non-Markovian regimes.In our analysis, we use concurrence [63] to measure the degree of entanglement, which is defined as

where λiare the eigenvalue ofρsin the decreasing order.whereis the complex conjugation of ρs.The quantum mutual information [64] is defined as

where S(ρs) is the von Neumann entropy.
In figure 3,we plotV,entanglement and quantum mutual information as functions of Δ and λ in the Markovian regime(γ=0).It can be seen from figure 3(a) thatV is small in the region of large Δ and small λ, which corresponds to the region that S1and S2can not get anti-synchronized.For weak coupling strength between S1and S2,V has a relative larger value when they are close to resonant.With the increase of λ,V has a relative larger value when the subsystems are a little detuned.With further increase of λ, the value of Δ at which the maximum value ofV arrived at is increasing.Meanwhile,the behavior of entanglement and quantum mutual information are shown in figures 3(b) and (c), respectively.Obviously, there is an apparent link between the visibility of synchronization, entanglement and quantum mutual information,and the behavior of them are approximately the same.That means in this case entanglement and quantum mutual information can reflect the visibility of the synchronization.In the previous studies, the relation among the Pearson coefficient, entanglement and quantum mutual information has been investigated widely.However,comparing figures 2 with 3,we find that the connection among the Pearson coefficient,entanglement and quantum mutual information is not obvious.

Figure 3.The diagram (a)–(c) displayV, concurrence and quantum mutual information as functions of Δ and λ in the Markovian regime(γ=0), respectively.We set J=0.3ω, ω1=ω, N=5000, and ωδt s 1 n = ωδt s 2n = ωδt s 1 s 2 =0.2.
Next,we investigate the relation amongV,entanglement and quantum mutual information in the non-Markovian regime.In figure 4, we plotV, entanglement and quantum mutual information withThe behavior ofV is consistent with entanglement and quantum mutual information once again.Comparing with figure 3, we find that the values ofV, concurrence and quantum mutual information in the non-Markovian regime are apparently larger than their Markovian counterpart.From numerical calculation we find that S1and S2approximately arrive at anti-synchronization with the collision times N ~5000 in the non-Markovian regime.As in the Markovian regime, when N ~2000 the subsystems approximately arrive at anti-synchronization.We display the synchronization between S1and S2in the Markovian regime at N=2000 in figure 5.Comparing figures 4 and 5, we can find that the behavior ofV,concurrence and quantum mutual information in the non-Markovian regime are very similar to that in the Markovian regime including the magnitude of those values.As we know,V, concurrence and quantum mutual information will decay as time evolves,but due to the information backflow in the non-Markovian regime they will decay slower than that in the Markovian regime.Thus, it takes more time forV, concurrence and quantum mutual information in the non-Markovian regime to decay to the same level as those in the Markovian regime.That is the reason why the non-Markovianity delay the phenomenon of anti-synchronization between the subsystems.
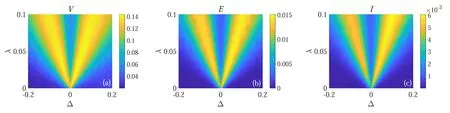
Figure 4.The diagram(a)–(c)displayV,concurrence and quantum mutual information as functions of Δ and λ in the non-Markovian regime respectively.We set J=0.3ω, ω1=ω, N=5000, and ωδt s 1 n = ωδt s 2n = ωδt s 1 s 2 =0.2.
Next, we further investigate the effect of non-Markovianity on the synchronization when the subsystems are detuned.We show the time evolution of the Pearson coefficient for different Δ in figure 6.Different color characterize different inner-environment interaction strength γ: the blue solid line characterizes γ=0, which means the environment is Markovian; the orange dashed lines, yellow dotted lines and purple dashed–dotted lines characterizerespectively, which indicate the non-Markovian environments.It can be seen from figure 6(a) that, in the case of resonance, the Pearson coefficient changes from 1 to -1 as time evolves,which indicates that S1and S2are synchronized at the beginning, and after a transient time, the two subsystems S1and S2lose their synchronization and gradually get anti-synchronized.In figures 6(b)and (c), we display C12for Δ=0.05ω and Δ=0.2ω, respectively.For a given Δ, from numerical calculation, we find that the non-Markovianity always delay the emergence of anti-synchronization, and it takes more time for S1and S2to get anti-synchronized with the increase of γ.On the other hand, for different Δ, two qubits S1and S2still arrive at anti-synchronization early in the Markovian regime compared with that in the non-Markovian regime.Compared with resonance,there is no obvious change in the time to get anti-synchronization for small Δ whether in the Markovian or non-Markovian regimes (see figure 6(b)),while it is slower to get anti-synchronized with large Δ for fixed γ (see figure 6(c)).Thus combine with figure 2,we can conclude that the detune between two qubits not only affects the degree of anti-synchronization, but also the time arriving at anti-synchronization.
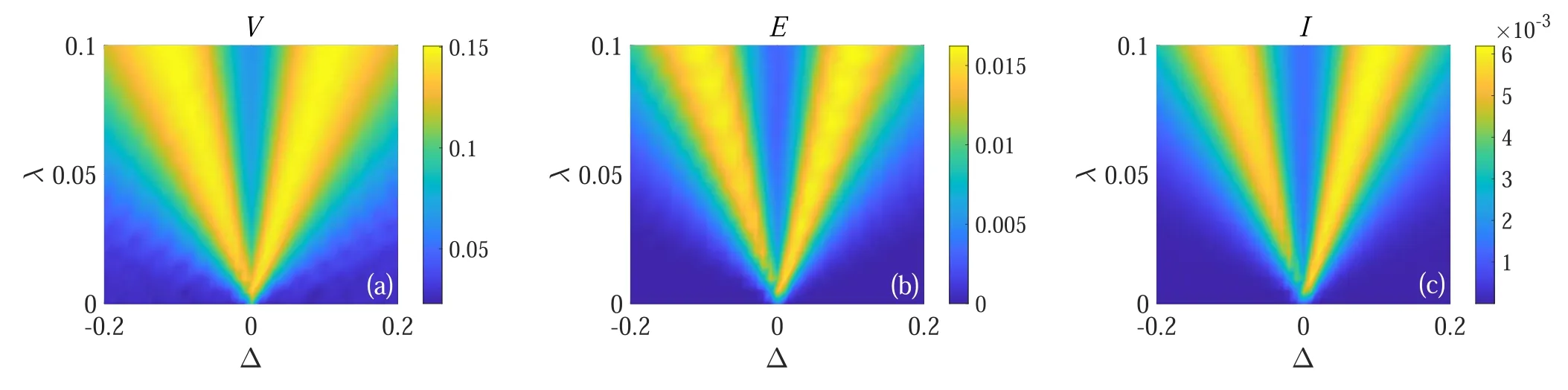
Figure 5.The diagram (a)–(c) displayV, concurrence and quantum mutual information as functions of Δ and λ in the Markovian regime(γ=0), respectively.We set J=0.3ω, ω1=ω, N=2000, and ωδt s 1 n = ωδt s 2n = ωδt s 1 s 2 =0.2.

Figure 6.The Pearson coefficient as a function of the collision times N for different Δ.In(a)Δ=0,(b)Δ=0.05ω,and(c)Δ=0.2ω.The blue solid lines, orange dashed lines, yellow dotted lines and purple dashed–dotted lines characterize γ=0,respectively.We set J=0.3ω, λ=0.1ω, ω1=ω, and ωδt s1 n =ωδt s 2n = ωδt s 1 s2 =0.2.
In the following,we investigate the effect of environment temperature on synchronization in the Markovian and non-Markovian regimes.We assume that the initial state of every identical environment ancilla is a thermal statewhere(we let k=1).And ω is the frequency of the identical environment ancilla.Obviously, in the limit T →0,the initial state of every identical environment ancilla reduces to ρe=|0〉〈0|.From numerical calculation we find that the synchronization between S1and S2for low temperature is similar to that when every ancilla of the environment is in the vacuum state.With the increase of T, we find that the region of the emergence of anti-synchronization is decreased gradually.In figure 7, we show the Pearson coefficient as a function of Δ and λ for T=5ω.Comparing figures 2 and 7,we can see that the region where C12~-1 is decreased compared with that in vacuum environment whether in the Markovian regime or non-Markovian regime.Comparing figures 7(a)(γ=0)and(b)we find that the behavior of Pearson coefficient in these two figures are similar for different Δ and λ.As expected, with the increase of T, the non-Markovianity becomes weak which leads to the behavior of synchronization in the non-Markovian regime approaches that in the Markovian regime.The increasing Δ always leads to the weakening of anti-synchronization between S1and S2,and the magnitude of λ which can compensate the effect of detune strongly depends on the temperature, more specifically,the higher the temperature,the larger the λ for fixed Δ.Meanwhile, as we know that heat bath leads to the decoherence of system,and increasing the temperature of the bath will make the coherent oscillations of〈σx〉damping severely,thus the amplitude of 〈σx〉 decreases significantly with the increasing temperature.Accordingly, for a longer evolution time,although the region where C12~-1 would be enlarged,the expectation value of the local observables would be extremely small before the Pearson coefficient approaches-1 in some region especially with large Δ and small λ.
To further investigate the effect of temperature on synchronization in the Markovian and non-Markovian regimes,we show the time evolution of the Pearson coefficient for different T in figure 8.We can see from figure 8 that,with the increase of T, there is no obvious change for the time to get anti-synchronized in the Markovian regime(see the blue solid lines).But the two qubits arrive at anti-synchronization early in the non-Markovian regime for high temperature with the same γ, for example, the subsystems get anti-synchronized early with the increasing of T for(see the yellow dotted lines).Thus the high temperature makes the synchronization in the non-Markovian regime with different γ close to that in the Markovian regime.Nevertheless, when the temperature is increased further, the magnitude of local observables would be extremely small before the Pearson coefficient approaches -1 in the most parameter region whether in the Markovian or non-Markovian regimes, and in this case the two qubits can not get anti-synchronized in the most region of the parameter space.


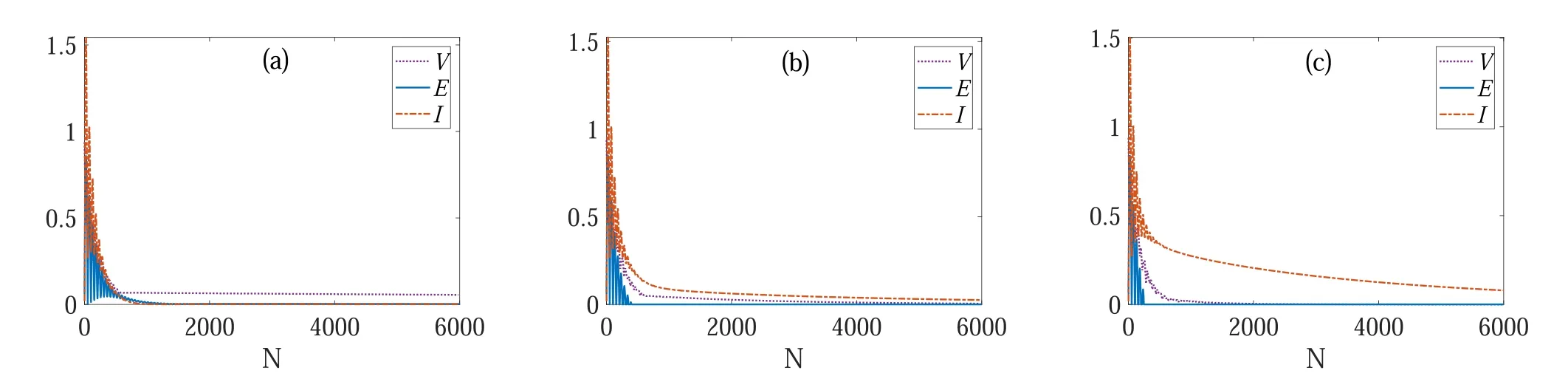
Figure 9.The diagram ofV, entanglement and quantum mutual information as functions of the collision times N for different T.In (a)T=0.1ω, (b) T=ω, and (c) T=5ω.The purple dotted lines, blue solid lines and orange dashed–dotted lines characterizeV, entanglement and quantum mutual information respectively.We set J=0.3ω, λ=0.1ω, Δ=0, γ=0 and ωδt s1 n =ωδt s 2n = ωδt s 1 s 2 =0.2.
In figure 9 we plotV,entanglement and quantum mutual information as functions of N for different temperature.From numerical calculation, we find that with the increase of T,V decreases as time evolves (see the purple dotted lines)because the incoherent pumping makes coherent oscillations of 〈σx〉 damping severely.When the amplitude of 〈σx〉decays, the synchronization between the subsystems gradually loses their visibility.Besides,we can see from figure 9(a)that in the low temperature case, after a transient damped oscillations, the entanglement reduces to a small value.Comparing with figure 8, we find that the entanglement has not vanished before the Pearson coefficient reaches -1 (see the blue solid lines).When the temperature increases, it can be seen from figure 9(b)that the entanglement reduces to zero in a very short time, and has vanished before the emergence of anti-synchronization.With further increase of T, as shown in figure 9(c), the entanglement vanishes faster than that in figure 9(b).This is the well known phenomenon named entanglement sudden death (ESD) which has been investigated widely in the past few years[65].For the model used in this paper,it is clear that the entanglement is not necessary for the anti-synchronization between the subsystems.Moreover,we can see from figure 9 that the quantum mutual information exhibit damped oscillations and then decrease rapidly for low temperature, but decays slowly with the increase of temperature(see the orange dashed–dotted lines).It is noted that for two qubits in the presence of of environment by using the Born–Markov master equation, a similar phenomenon that,the ESD emerges while the quantum mutual information still exists for high temperature of the environment has already been observed [66].From above result it can be concluded that the increase of environment temperature breaks the correspondence among the visibility of synchronization, entanglement and quantum mutual information in our model.
4.Conclusions
In this paper we have investigated the transient quantum spontaneous synchronization between two qubits interacting with a common non-Markovian environment based on a collision model.We have mainly explored the effect of non-Markovianity on the synchronization between two qubits.We have found that, in some situation, even though the Pearson coefficient approaches -1, there is no visibility of synchronization because the local observables are extremely small,and in this case we argue that the subsystems are not antisynchronized.Thus, we definedV to characterize the visibility of synchronization as an auxiliary after the Pearson coefficient C12~-1.Particularly,we have found an obvious connection amongV, entanglement and quantum mutual information when every environment ancilla is in the vacuum state whether in the Markovian or non-Markovian regimes.Comparing with the behavior of synchronization in the Markovian regime, we have found that the region of emergence of anti-synchronization is decreased in the non-Markovian regime.Meanwhile, it is always slower to get antisynchronized in the non-Markovian regime compared with that in the Markovian regime, and with the increase of non-Markovianity, it takes more time for the subsystems to get anti-synchronized.
In addition,we have studied the effect of the environment temperature on the synchronization between the subsystems.With the increase of temperature, the behavior of synchronization in the non-Markovian regime gradually approaches that in the Markovian regime.Meanwhile, the high temperature decreases the parameter region of the emergence of antisynchronization in both Markovian and non-Markovian regimes, and it also leads to the connection amongV,entanglement and quantum mutual information broken.
Acknowledgments
This work is financially supported by the National Natural Science Foundation of China (Grant Nos.11775019 and 11875086).
 Communications in Theoretical Physics2021年10期
Communications in Theoretical Physics2021年10期
- Communications in Theoretical Physics的其它文章
- Analysis of the wave functions for accelerating Kerr-Newman metric
- Three-dimensional massive Kiselev AdS black hole and its thermodynamics
- Examination of n-T9 conditions required by N=50, 82, 126 waiting points in r-process
- Scalar one-loop four-point integral with one massless vertex in loop regularization
- Strange quark star and the parameter space of the quasi-particle model
- Improved analysis of the rare decay processes of Λb
