The Reflexive Selfadjoint Solutions to Some Operator Equations
Wenting Liang and Chunyuan Deng
1 Department of Mathematics,Taiyuan Normal University,Jinzhong 030619,Shanxi,China.
2 School of Mathematical Science,South China Normal University,Guangzhou 510631,China.
Abstract.In this paper,we study the existence of the reflexive,reflexive selfadjoint and reflexive positive solutions to some operator equations with respect to the generalized reflection operator dual(P,Q).We derive necessary and sufficient conditions for the solvability of these equations and provide a detailed description of the solutions in the solvable case by using the Moore-Penrose inverses.
Key words:(P,Q)reflexive solution,operator equation,positive operator.
1 Introduction
Let H and K be separable,infinite dimensional,complex Hilbert spaces.We denote the set of all bounded linear operators from H into K by B(H,K)and by B(H)when H=K.For A∈B(H,K),let A*,R(A)and N(A)be the adjoint,the range and the null space of A,respectively.is the closure of R(A).An operator A∈B(H)is said to be injective if N(A)={0}.A is densely defined if the domain of A is a dense subset of H and the range of A is contained within H.A is said to be positive if(Ax,x)≥0 for all x∈H.Note that the positive operator A has a unique square root A12.Let PMbe the orthogonal projection on closed subspace M?H.IMdenotes the identity onto M or I if there is no confusion.For A,B,P,Q∈B(H),denote by

We say that P∈B(H)is a reflection operator if P*=P and P2=I.For two reflection operators P and Q,denote by
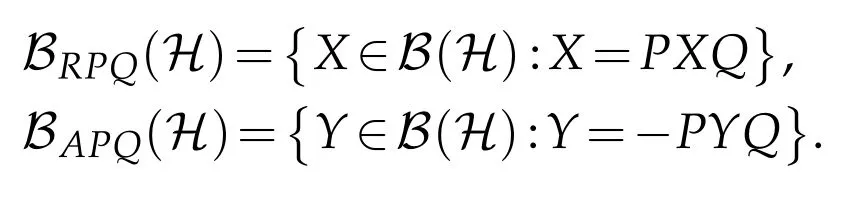
The operator X∈BRPQ(H)(resp.Y∈BAPQ(H))is said to be(P,Q)reflexive(resp.(P,Q)anti-reflexive)operator with respect to the reflection operator pair(P,Q)[2,3].By BS(H)and B+(H)we denote the set of all selfadjoint elements and all positive elements in B(H),respectively.Denote by
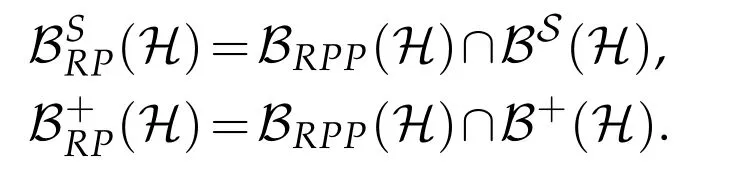
The(P,Q)reflexive and anti-reflexive operators have many applications in system and control theory,in engineering,in scientific computations and various other fields[2,3,5,15].The positive solutions to the equation AX=C were studied in[6-8,13,14,19,20]for different setting in Hilbert space or Hilbert C*-module.The equation XA*-AX*=B was studied in[1,9].
The purpose of this paper is to provide a new approach to the study of(P,Q)reflexive solution and(P,P)reflexive self-adjoint and(P,P)reflexive positive solution respectively to the operator system AX=B.We get the necessary and sufficient conditions for the existence of a solution and obtain the general expression of the solution in the solvable case.
The paper is organized in the following way.In Section 2,we will recall some results about operators on Hilbert space.In Section 3,we will give the necessary and sufficient conditions for the existence of a(P,Q)reflexive solution to the operator equation AX=B and provide a formula for the general solution to this operator equation.In Section 4,we consider the existence and expressions for the(P,Q)reflexive and anti-reflexive solutions to the operator equation AXB=C.In Section 5,we apply the obtained results to study the(P,Q)reflexive solution and(P,P)reflexive self-adjoint solution to the operator system AX=B and XC=D.A new result concerning the(P,Q)reflexive solution of the operator equation A*X+X*A=B is derived in this section.
2 Some lemmas
In this section,we begin with some lemmas which play important roles in the sequel.First,we give the properties of reflection operator.If P2=I,σ(P)k=0,1}={1,-1}by the spectral mapping theorem.Observing that ifλ∈σ(P),thenλ2=1.This shows that eachλ∈σ(P)is a simple root of the equationλ2=1.
Lemma 2.1.Let P∈B(H).Then P is a reflection operator(P*=P and P2=I)if and only if P=IM⊕-IM⊥,where M=R(I+P).
Let H1=R(I+Q),H2=R(I-Q),K1=R(I+P)and K2=R(I-P)be nondegenerate subspaces.Then reflection operator P as an operator on K1˙+K2and reflection operator Q as an operator on H1˙+H2have the diagonal matrix forms

respectively.Let A,B and X∈B(H)be partitioned as

respectively.It is clear that
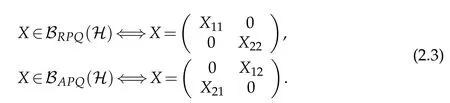
The following lemma is a standard result.
Lemma 2.2.For A∈B(H),let A=UP0be the polar decomposition of A,where U is unitary fromtoand P0=|A|=λdEλis the spectral decomposition of P0.Let,where

Then

Note that A?=(A*A)?A*=A*(AA*)?,R(A)is closed if and only if R(P0)is closed and if and only if 0 is not an accumulation point ofσ(P0).We getand A?=A?if R(A)is closed,where A?∈B(H)is the Moore-Penrose inverse of A.In general,A?is a closed densely defined operator if R(A)is not closed[4,18].Throughout this work the next well-known criterion due to Douglas[10](see also Fillmore-Williams[12])about range inclusions and factorization of operators will be crucial.
Lemma 2.3([10]).If A,B∈B(H),then the followings are equivalent:
(i)A=BC for some operator C∈B(H);
(ii)AA*≤kBB*for some k>0;
(iii)R(A)?R(B).
If one of these conditions holds,then there exists a unique solution C0∈B(H)of the equation BX=A such that R(C0)?R(B*)and N(C0)=N(A).This solution is called the Douglas reduced solution.Moreover,‖C0‖2=inf{λ>0:AA*≤λBB*}.In fact,if R(A)?R(B),the Douglas reduced solution is C0=B?A.If R(A)?R(B)and R(B)is closed,then the Douglas reduced solution is C0=B?A.
The following lemma presents general solutions of the operator equation AX=B(see[5-7,13,15,19]).
Lemma 2.4.Let A,B be given operators in B(H).Then the operator equation AX=B has a solution if and only if R(B)?R(A)and the general solution is X=A?B+(IA?A)Y,where Y∈B(H)is arbitrary.
3 The(P,Q)reflexive solution
In this section we consider the existence and expression for the reflexive,reflexive self-adjoint and reflexive positive solution of the operator equation AX=B,respectively.
Theorem 3.1.Let A,B be given operators in B(H),P,Q be reflection operators and AP,BQbe defined in(1.1).Then the following statements hold.
(i)AX=B has a(P,Q)reflexive solution X∈BRPQ(H)if and only if R(BQ)?R(AP).The general(P,Q)reflexive solution is

where Y∈BRPQ(H)is arbitrary.
(ii)AX=B has a(P,Q)anti-reflexive solution X∈BAPQ(H)if and only if R(B-Q)? R(AP).The general(P,Q)anti-reflexive solution is

where Y∈BAPQ(H)is arbitrary.
Proof.(i)By(1.1),(2.1)and(2.2),AX=B has a solution X∈BRPQ(H),i.e.,
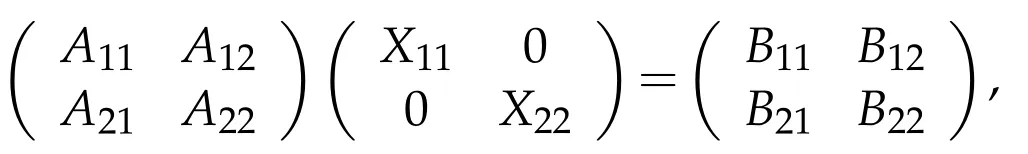
if and only if
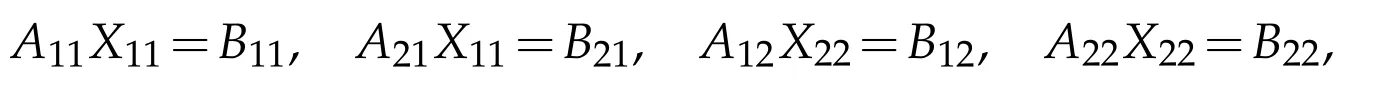
or else if and only if

which is equivalent with APX=BQhas a solution X∈BRPQ(H).By Lemma 2.3,we get R(BQ)?R(AP).
Conversely,if R(BQ)?R(AP),by Lemma 2.2,

We get

Since[P,A*A+PA*AP]=0,we get[P,(A*A+PA*AP)?]=0 and
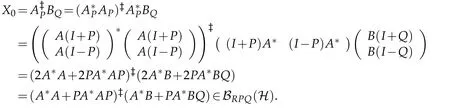
Note that,for every Y∈BRPQ(H),
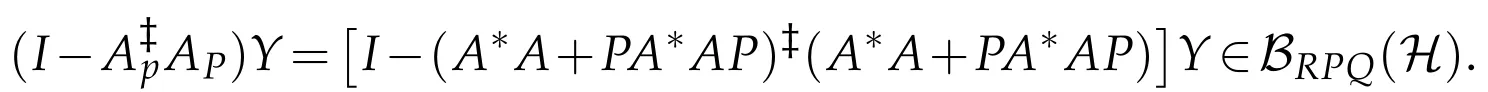
Since R(A*)?R(A*A+PA*AP),we get


(ii)Note that AX=B has a solution X∈BAPQ(H)if and only if

has a solution X∈BAPQ(H)or else if and only if

has a solution X∈BAPQ(H)or else if and only if APX=B-Qhas a solution X∈BAPQ(H).The rest of the proof is similar to item(i).
Remark 3.1.If A∈B(H)and P is a reflection operator,then

and
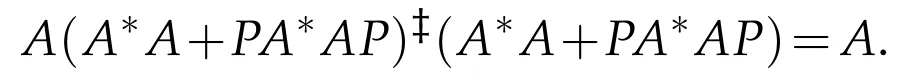
In Theorem 3.1(i),if R(A*A+PA*AP)is closed,the general reflexive solution reduces as
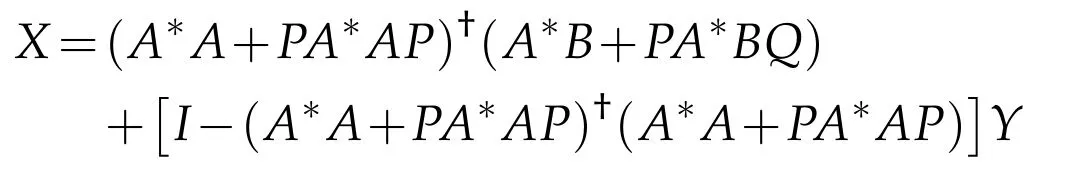
for all Y∈BRPQ(H).If R(A)is closed and P=Q=I,then the general reflexive solution reduces as X=A?B+(I-A?A)Y,?Y∈B(H).
When P=Q we can seek the reflexive selfadjoint solution of AX=B.
Theorem 3.2.Let A,B be given operators in B(H),P be a reflection operator and AP,BPbe defined in(1.1).Then AX=B has a solution X∈(H)if and only if R(BP)?R(AP)and{AB*,APB*}?BS(H).The general(P,P)reflexive selfadjoint solution is
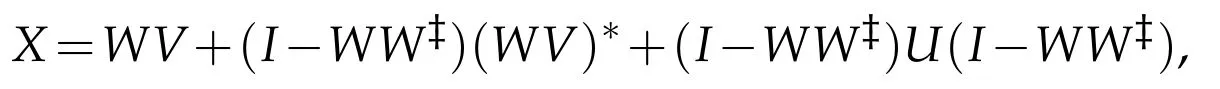
where W=(A*A+PA*AP)?,V=A*B+PA*BP and U∈(H)is arbitrary.
Proof.By the proof of Theorem 3.1,if the equation AX=B has a solution X∈=BRPP(H)∩BS(H),then R(BP)?R(AP).Moreover,

is selfadjoint.Hence,the operators B(I±P)A*are selfadjoint,which is equivalent to AB*,APB*∈BS(H).The necessity follows.
For sufficiency,from R(BP)?R(AP)we know there exists X∈B(H)such that APX=BPby Douglas’s theorem.If APis represented by

where A11is an injective and densely defined operator,then BPcan be written as
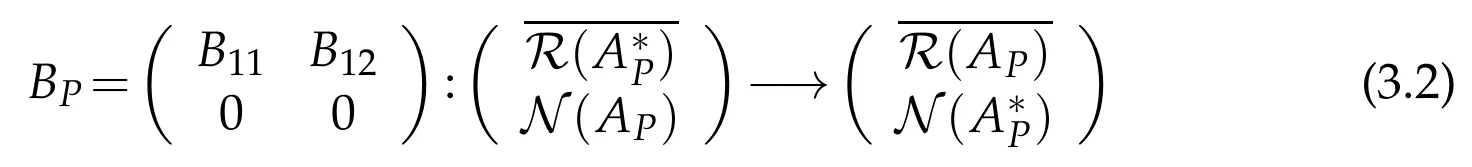
since R(BP)?R(AP).X∈B(H)as the corresponding 2×2 operator matrix can be represented by

The relation APX=BPimplies that A11X11=B11and A11X12=B12.Since A11is injective and densely defined,we get X11=B11and X12=B12.The general selfadjoint solution of APX=BPis

From

we get that AX=B.Hence,(3.4)is the general selfadjoint solution of AX=B.If{AB*,APB*}?BS(H),then AP∈BS(H).Applying(3.1)and(3.2)we get

The general selfadjoint solution(3.4)can be represented as

Set W:=(A*A+PA*AP)?and V:=A*B+PA*BP.Then
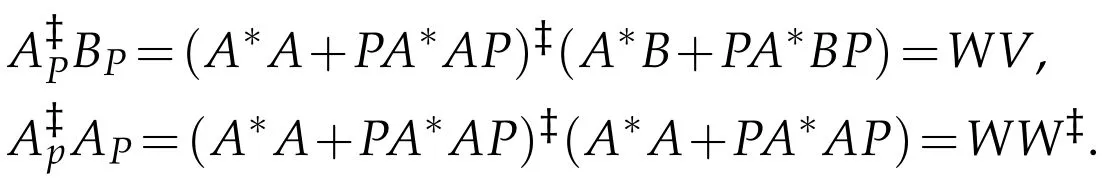
The general selfadjoint solution(3.5)can be represented as

Note that{W,W?,V}?BRPP(H).If U∈(H),we get that X∈(H)is a general reflexive selfadjoint solution of AX=B.
The general reflexive positive solution of AX=B is given as the following.
Theorem 3.3.Let A,B be given operators in B(H)and P be a reflection operator.Then AX=B has a solution X∈(H)if and only if
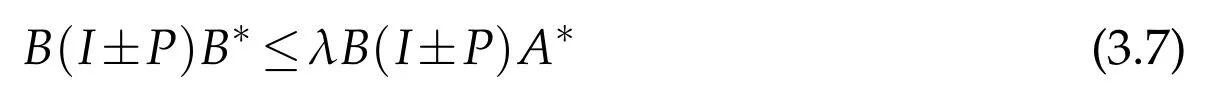
for someλ>0.A general(P,P)reflexive positive solution of AX=B is

where W=(A*A+PA*AP)?and U∈(H)is arbitrary.
Proof.As follows from the proof of Theorem 3.1,the equation AX=B has a solution X∈(H)=BRPP(H)∩B+(H)if and only if the equation APX=BPhas a solution X∈(H).
Let Y be a positive solution of APX=BP.Since R(BP)=R(APY)?R(AP),by Douglas’s theorem,there existsλ>0 such that

Note that

Hence,B(I±P)B*≤λB(I±P)A*for someλ>0.Conversely,if the conditions(3.7)are satisfied with someλ>0,thenBy Lemma 2.3,there exists a unique


Let APand BPbe partitioned as(3.1)and(3.2),respectively.Then X0can be partitioned as
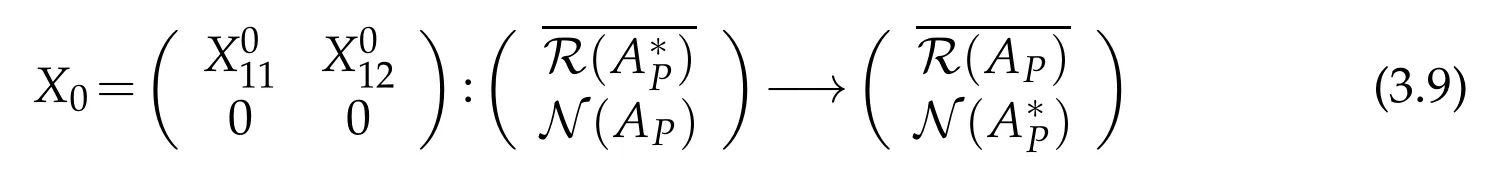
since R(X0)?Note that the relation N(X0)=N(BP)implies N=From
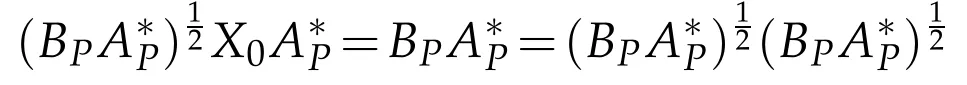
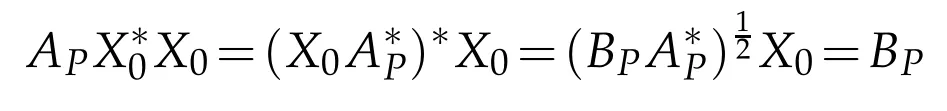
and(3.8),we know that
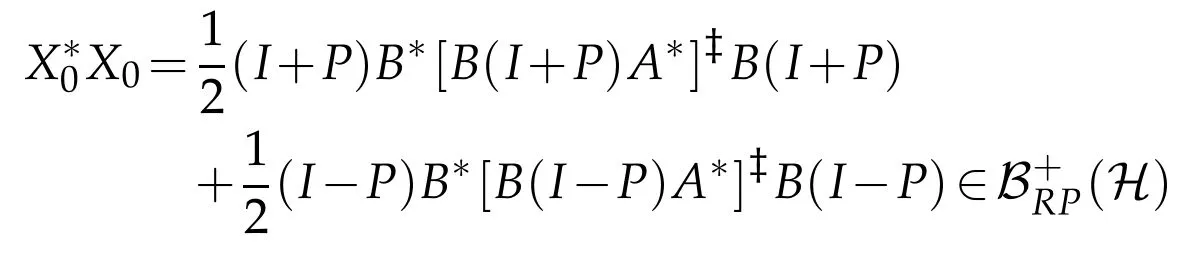
is a(P,P)reflexive positive solution to APX=BP.It implies thatis a(P,P)positive reflexive solution to AX=B and the general(P,P)positive reflexive solution to AX=B is
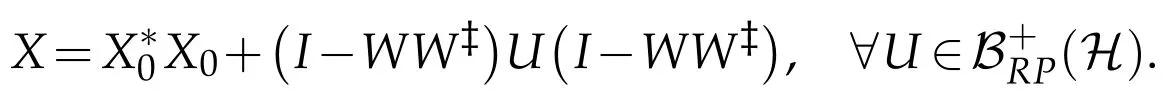
The proof is complete.
If A is selfadjoint and AX=B has a selfadjoint solution X0,then

where the bar denotes complex conjugation.The product AX0=B is invertible if and only if the selfadjoint operators A and X0are invertible.
4 The(P,Q)reflexive(anti-reflexive)solutions to AXB=C
In this section we study(P,Q)reflexive and anti-reflexive solutions to the operator equation AXB=C.Note that solution X∈B(H)is(P,Q)reflexive(antireflexive)if and only if X*∈B(H)is(Q,P)reflexive(anti-reflexive).
Theorem 4.1.Let A,B and C be given operators in B(H),P,Q be reflection operators.Then the following statements hold.
(i)The operator equation AXB=C has a(P,Q)reflexive solution if and only if R(C)?R(A)and there exists Y0∈B(H)such that

where[A?C+(I-A?A)Y0]Pand BQare defined by(1.1).
(ii)The operator equation AXB=C has a(P,Q)anti-reflexive solution if and only if R(C)?R(A)and there exists S0∈B(H)such that
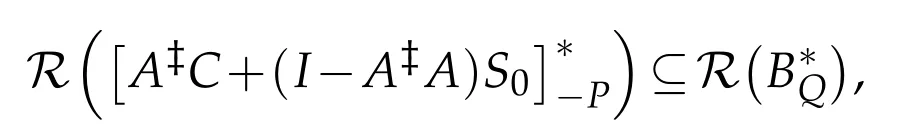
where[A?C+(I-A?A)S0]-Pand BQare defined by(1.1).
Proof.(i)Necessity.If the operator equation AXB=C has(P,Q)solutions,the Douglas’s Theorem[10]or Lemma 2.3 yields R(C)?R(A).Let X0∈BRPQ(H)be such that AX0B=C.It follows from Lemma 2.4 that there exists Y0∈B(H)such that the operator equation XB=A?C+(I-A?A)Y0has a(P,Q)reflexive solution X0.Therefore,the operator equation B*X*=[A?C+(I-A?A)Y0]*has a(Q,P)reflexive solutionBy Theorem 3.1(i),we obtain that R([A?C+(I-
For sufficiency,if there exists Y0∈B(H)such that R([A?C+(I-A?A)Y0])?R(),by Theorem 3.1(i)again,then the operator equation B*Y=[A?C+(IA?A)Y0]*has a(Q,P)reflexive solution(i.e.,X0is a(P,Q)reflexive solution).That is,
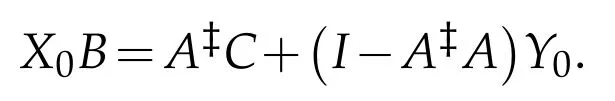
Note that R(C)?R(A),it follows that there exists a(P,Q)reflexive solution X0such that AX0B=C.
(ii)Note that,by Theorem 3.1(ii),the operator equation B*Y=[A?C+(IA?A)Y0]*has a(Q,P)anti-reflexive solution(i.e.,X0is a(P,Q)anti-reflexive solution)if and only if R([A?C+(I-A?A).The rest of the proof is similar to(i).
Next,we give the expression of(P,Q)reflexive and anti-reflexive solution to operator equation AXB=C.By Theorem 4.1,if there exists Y0∈B(H)such that R([A?C+(I-A?A),then the operator equation

has a(Q,P)reflexive solution,that is,a(P,Q)reflexive solution X0.Denote by W0=A?C+(I-A?A)Y0.By Theorem 3.1,we obtain that the(Q,P)reflexive solution to B*Y=is

where Y∈BRPQ(H)is arbitrary.So,we get

where Y∈BRPQ(H)is arbitrary,is a(P,Q)reflexive solution to the operator equation
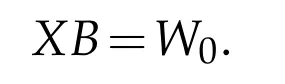
Moreover,note that R(C)?R(A),it is easy to see that AX0B=AW0=C.As a result,the(P,Q)reflexive solution to AXB=C is
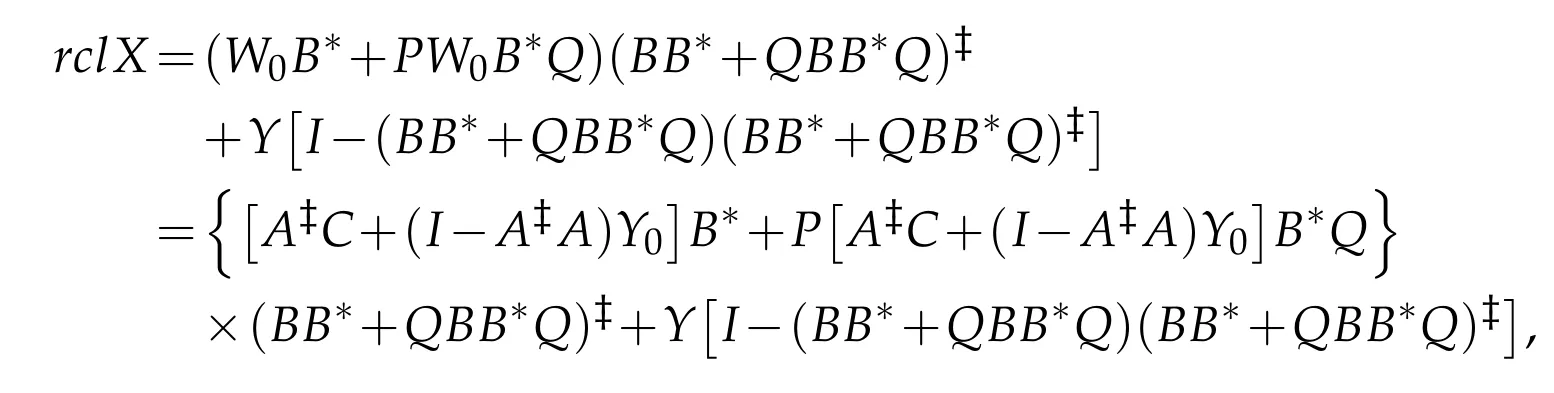
where Y∈BRPQ(H)are arbitrary.
Therefore,we have the following result.
Theorem 4.2.Let A,B and C be given operators in B(H),P,Q be reflection operators.Then the following statements hold.
(i)If there exists Y0∈B(H)such that

then the operator equation AXB=C has(P,Q)reflexive solution
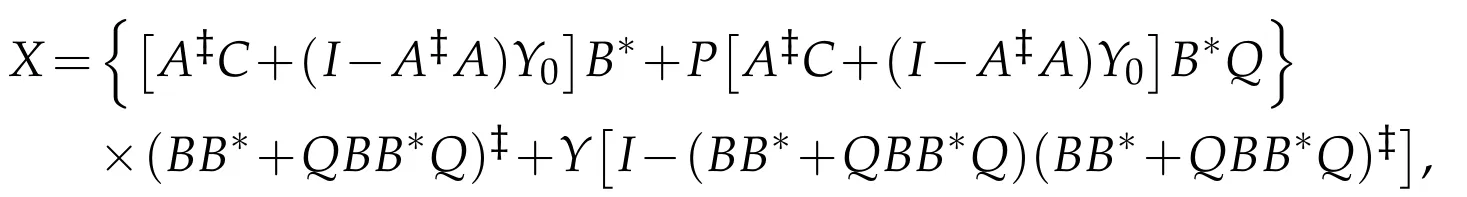
where Y∈BRPQ(H)are arbitrary.

then the operator equation AXB=C has(P,Q)anti-reflexive solution
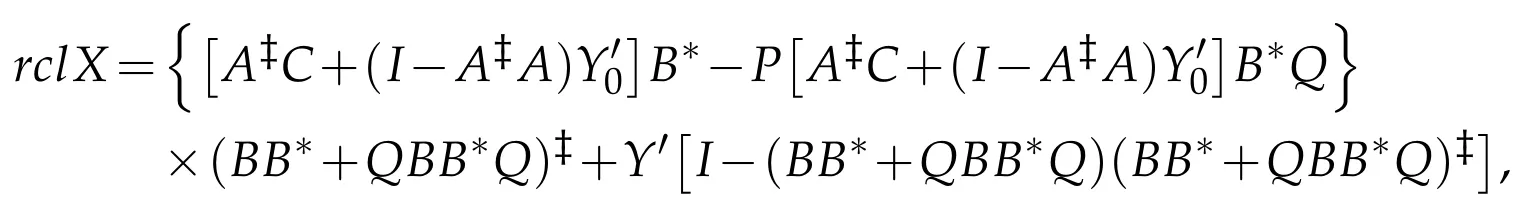
where Y′∈BAPQ(H)are arbitrary.
5 Apply to the operator system
In this section,we investigate the common reflexive solution of the equations AX=B and X*C=D.For matrices,the necessary and sufficient conditions for the existence of the common hermitian solution of linear matrix equations were studied in[14,Theorem 2.3]and[16,Theorem 4].Let
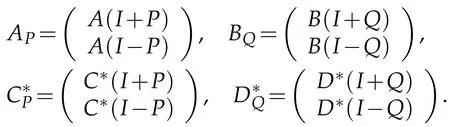
The following theorem gives general conditions for the existence of reflexive solutions.
Theorem 5.1.Let A,B,C and D be given operators in B(H),and P,Q be reflection operators.
(i)The equations AX=B and X*C=D have a common solution X∈BRPQ(H)if and only if

The common(P,Q)reflexive solution is
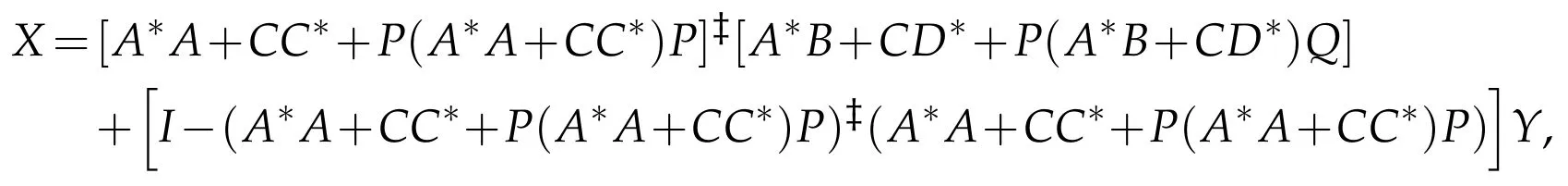
where Y∈BRPQ(H)is arbitrary.
(ii)The equations AX=B and XC=D have a common solution X∈(H)if and only if the following conditions hold:
(a)AD=BC and APD=BPC;
(b){AB*,APB*,C*D,C*PD}?BS(H);
(c)R

The common(P,P)selfadjoint reflexive solution is
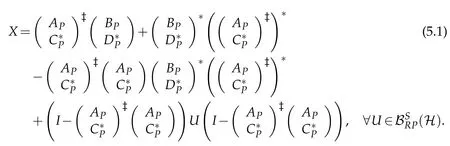
Proof.(i)By the proof of Theorem 3.1,the equations AX=B and X*C=D have a common solution X∈BRPQ(H)if and only if
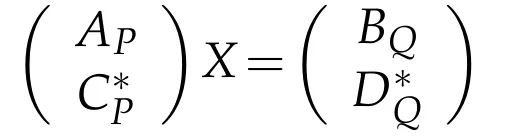
has a solution X∈BRPQ(H)or else if and only if
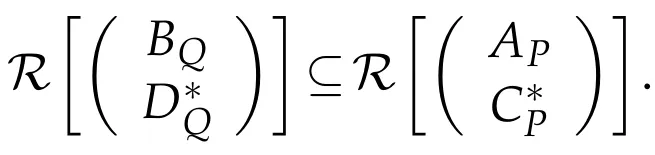
By Theorem 3.1,for all Y∈BRPQ(H),the general common solution is

(ii)By Theorem 3.2,the system AX=B and XC=D has a solution X∈(H)if and only if


and
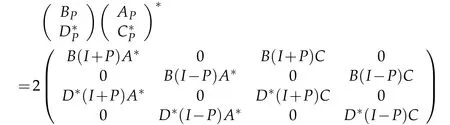
is selfadjoint,which is equivalent to AD=BC,APD=BPC and{AB*,APB*,C*D,C*PD}?BS(H).By Theorem 3.2,the general selfadjoint solution is

The proof is complete.
The next theorem represents general conditions for the existence of a reflexive solution of the operator equation A*X+X*A=B.
Theorem 5.2.Let A,B∈B(H).If A,B have the matrix representations(2.2),then A*X+X*A=B has a solution X∈BRPQ(H)if and only if the following system of matrix equations

is consistent.In this case,the(P,Q)reflexive solution is represented by
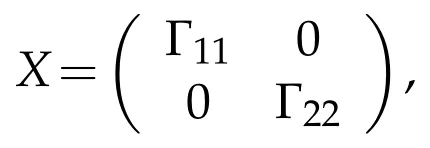
where
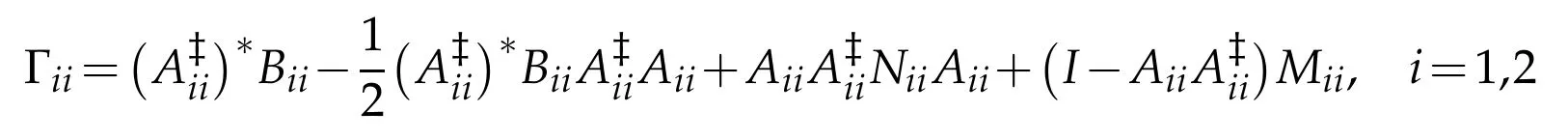
for all Mii,Niisuch that
Proof.First,by(2.3),there exist X11and X22such that X=X11⊕X22if X∈BRPQ(H).Note that B=B*if A*X+X*A=B.By(2.2),A*X+X*A=B has a solution X∈BRPQ(H)if and only if there exist X11and X22such that

i.e.,the system of(5.2)has a solution.In order to describe the set of reflexive solutions completely,we divide the proof into several steps.
Claim 1.For every A0∈B(H),the equation=0 has the general solutionM0for all M0,N0such thatA0=0.
Proof.As we know,A0as an operator frominto H=has the diagonal matrix formwhere∈is densely defined and injective.Let X0=have the corresponding form with A0.From

we get
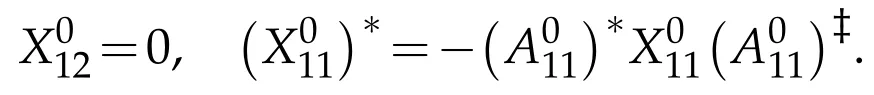

Claim 2.For every A0,B0∈B(H),if there exists X0∈B(H)such that=B0,then B0is selfadjoint and

Proof.It is clear that B0is selfadjoint.Since=0 and(I-=0,we get=0.The result follows immediately.
Claim 3.For every A0,B0∈B(H),the equation=B0has one special solution
Proof.By Claim 2,

Hence,by Claims 1-3,the general solution of=Bii,i=1,2 is
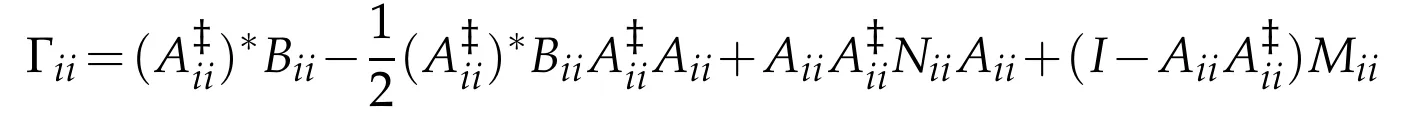
for all Mii,Niisuch that=0.We get the general(P,Q)reflexive solution

where Miiis arbitrary and Niisatisfies=0.
6 Concluding remarks
Using Moore-Penrose inverses,we give the necessary and sufficient conditions for the solvability of some operator equations and provide a detailed description of the solutions if the corresponding equations are consistent.
In details,we investigate the existence and expressions for the(P,Q)reflexive,the(P,P)reflexive selfadjoint and the(P,P)reflexive positive solutions respectively to the operator system AX=B,the(P,Q)reflexive and anti-reflexive solutions to the operator equation AXB=C.Also,by applying the obtained results,we study the(P,Q)reflexive solution and the(P,P)reflexive self-adjoint solution to the operator system AX=B and XC=D.A new result concerning the(P,Q)reflexive solution of the operator equation A*X+X*A=B is derived.
 Communications in Mathematical Research2021年2期
Communications in Mathematical Research2021年2期
- Communications in Mathematical Research的其它文章
- Weighted and Maximally Hypoelliptic Estimates for the Fokker-Planck Operator with Electromagnetic Fields
- On the J.L.Lions Lemma and Its Applications to the Maxwell-Stokes Type Problem and the Korn Inequality
- A Level Set Representation Method for N-Dimensional Convex Shape and Applications
- Spectral Properties of an Energy-Dependent Hamiltonian
