On the J.L.Lions Lemma and Its Applications to the Maxwell-Stokes Type Problem and the Korn Inequality
Junichi Aramaki
Division of Science,Tokyo Denki University,Hatoyama-machi,Saitama,350-0394,Japan.
Abstract.In this paper,we consider the equivalent conditions with Lp-version(1<p<∞)of the J.L.Lions lemma.As applications,we first derive the existence of a weak solution to the Maxwell-Stokes type problem and then we consider the Korn inequality.Furthermore,we consider the relation to other fundamental results.
Key words:J.L.Lions lemma,de Rham theorem,Maxwell-Stokes type problem,multiply-connected domain.
1 Introduction
Assume thatΩis a domain of Rd.In this paper,this means thatΩis a bounded and connected open subset of Rdwhose boundaryΓ=?Ωis Lipschitz-continuous andΩis locally on the same side ofΓ.The classical J.L.Lions lemma asserts that any distribution in the space of H-1(Ω)with the gradient(in the distribution sense)belonging to H-1(Ω)is a function in L2(Ω).
Amrouche et al.[1]derived the equivalent conditions with the J.L.Lions lemma.The conditions are the classical and the general J.L.Lions lemma,the Ne?as inequality,the coarse version of the de Rham theorem,the surjectivity of the operator div:and an approximation lemma.Some of these equivalent properties can be given as a”direct”proof.
However,these equivalent conditions of L2-version of the J.L.Lions lemma are insufficient for considering the Maxwell-Stokes type system containing p-curlcurl operator.Thus it is important for us to improve the result to the Lp-version of the equivalent relations with the J.L.Lions lemma.
One of our purpose of this paper is to show the existence of a weak solution to the Maxwell-Stokes type equation.The existence depends deeply on the nonlinearity of the equation and the shape of the domain.We allow the domainΩ to be a multiply-connected domain with holes.To show the existence,we apply the equivalent conditions with the J.L.Lions lemma,in particular,the coarse version of the de Rham theorem.For example,Lp-version of the Ne?as inequality can be found in Ne?as[19,Theorem 1],Geymonat and Suquet[14,Lemma 1]and Amrouche and Girault[2].For the Maxwell type system containing p-curlcurl operator,see Miranda et al.[17,18]and Aramaki[6],and for the Maxwell-Stokes type system,see Pan[20]and Aramaki[9]and references therein.
The paper is organized as follows.In Section 2,we give some preliminaries.In Section 3,we derive Lp-version of the J.L.Lions lemma and its equivalent relations.In Section 4,we give an application on the existence of a weak solution to the Maxwell-Stokes type problem.Section 5 is devoted to consider the Korn inequality.In the Appendix A,we give a relation between the J.L.Lions lemma and the de Rham theorem,and in the Appendix B,we give a relation between the J.L.Lions lemma and a weak version of Poincar′e lemma.
2 Preliminaries
In this section,we shall state some preliminaries that are necessary in this paper.LetΩbe a domain in Rd(d≥2)(which means a bounded,connected open subset of Rdwith a Lipschitz-continuous boundaryΓ),let 1<p<∞and let p′be the conjugate exponent i.e.,(1/p)+(1/p′)=1.From now on we use D(Ω),Lp(Ω),Wm,p(Ω),,W-m,p(Ω)=(the dual space of,m≥0,integer),Ws,p(Γ)(s∈R),and so on,for the standard real C∞functions with compact supports inΩ,Lpand Sobolev spaces of real valued functions.For any above space B,we denote Bdby boldface character B.Hereafter,we use this character to denote vector and vector-valued functions.Occasionally,we also use the same character for matrix values functions,and we denote the standard inner product of vectors a and b in Rdby a·b.We denote the space of distributions in Ωby D′(Ω).Moreover,for the dual space B′of B(resp.B′ofB),we denote the duality bracket between B′and B(resp.B′andB)by〈·,·〉B′,B(resp.〈·,·〉B′,B).
The gradient operatorgrad=?:D′(Ω)→D′(Ω)is defined by
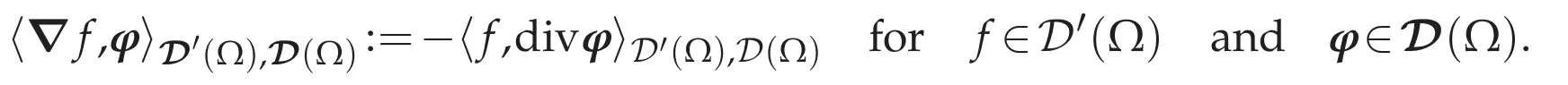
SinceΩis connected,we can see that if f∈D′(Ω)satisfies ?f=0 in D′(Ω),then f is identified with a constant function(cf.Boyer and Fabrie[10,Chapter II,Lemma II.2.44]).For f∈Lp(Ω),we can regard?f as an element ofW-1,p(Ω)by the definition

The operator curl:D′(Ω)→D′(Ω;Rd(d-1)/2)is defined by
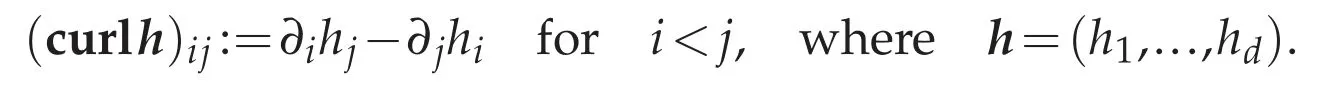
The classical Poincar′e lemma says that whenΩis simply connected domain of Rd,forh∈C1(Ω),there existsπ∈C2(Ω)such thath=?πinΩif and only ifcurlh=0 inΩ.
We introduce a closed subspace of a reflexive Banach spacewhich is a basic space in our arguments by

Moreover,we define a closed subspace of Lp′(Ω)by

endowed with the norm of Lp′(Ω).We note that the dual space(Lp(Ω)/R)′of Lp(Ω)/R is identified with.Now we state three theorems on the properties of the domainΩwithout their proofs.
Theorem 2.1.LetΩbe a domain of Rd.Then there exist a finite number of domains Ωi?Ω(i∈I)such that eachΩiis starlike with respect to an open ball andΩ=∪i∈IΩi,whereΩiis starlike with respect to an open ball B(x,r)={y∈Rd;|y-x|<r}means that if for each z∈Ωi,the convex hull of{z}∪B(x,r)is contained inΩi.
For the proof,see Maz’ya[16,Section 1.1.9,Lemma 2].
Theorem 2.2.LetΩbe a domain of Rd.Then there exist domainsΩj(j=1,2,...)of Rdsuch that the boundary?Ωjis of class
For the proof,see[10].
Theorem 2.3.LetΩbe a domain of Rd.Then there exist a finite number of simply connected domainsΩi(i∈I)of Rdsuch thatΩ=∪i∈IΩi.
For the proof,see[1].
3 Lp-version of the J.L.Lions lemma and its equivalent relations
In this section,we assume thatΩis a bounded domain of Rdwith a Lipschitzcontinuous boundary.
We derive the following theorem.
Theorem 3.1.LetΩbe a domain and 1<p<∞.Then the following(a),(b),...,(g)are equivalent.
(a)Classical J.L.Lions lemma:If f∈W-1,p(Ω)satisfies

then f∈Lp(Ω).
(b)The Ne?cas inequality:There exists a constant C=C0(p,Ω)such that

(c)The operator grad has a closed range:grad(Lp(Ω)/R)is a closed subspace ofW-1,p(Ω).
(d)Coarse version of the de Rham theorem:For anyh∈W-1,p(Ω),there exists a unique[π]∈Lp(Ω)/R,where[π]denotes the class in the quotient space Lp(Ω)/R with the representativeπ,such thath=?πinW-1,p(Ω)if and only if

(e)The operator div is surjective:The operator

is continuous and surjective.Consequently,for any,there exists a unique/Kerdiv,whereKerdiv=(Ω,div0)and[uf]denotes the class in the quotient space/Kerdiv with the representativeufsuch that div[uf]=f inΩ.Therefore,the operator

is continuous and bijective.Hence,by the Banach open mapping theorem,there exists a constant c1(p,Ω)>0 such that

(f)Approximation lemma:LetΩis starlike with respect to an open ball and define


where c2(p′,Ω)>0 is a constant,and

(g)The J.L.Lions lemma:If f∈D′(Ω)satisfies?f∈W-1,p(Ω),then f∈Lp(Ω).
Remark 3.1.The authors of[1]derived this theorem in L2-framework,for example,in(a),in the sense that f∈H-1(Ω)and ? f∈H-1(Ω)implies f∈L2(Ω).Therefore,our Theorem 3.1 is an improvement of[1].This improvement is necessary to consider in applications to the Maxwell-Stokes problem containing pcurlcurl equation in Section 4 and the Korn inequality in Section 5.
Proof of Theorem 3.1
(a)implies(b).Define a Banach space equipped with the norm

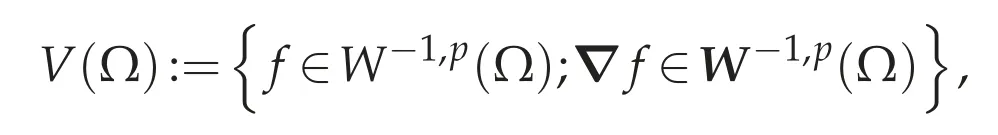
The canonical injection i:Lp(Ω)→V(Ω)is linear,continuous and bijective according to(a).Hence,it follows from Banach open mapping theorem that i-1is also continuous,that is,there exists a constant c0(p,Ω)>0 such that

(b)implies(c).It suffices to show that there exists a constant C(p,Ω)>0 such that

If the inequality(3.1)is false,then there exists a sequence{[fk]}?Lp(Ω)/R such that
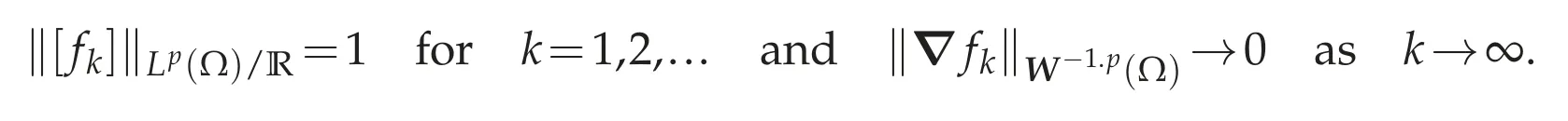

is compact and i0is the dual operator of the compact injection,we can see that fkl→f strongly in W-1,p(Ω).On the other hand,since?fkl→0 inW-1,p(Ω),it follows from the hypothesis(b)that we can see that{fkl}is a Cauchy sequence in Lp(Ω).Hence fkl→f strongly in Lp(Ω)as l→∞.Since?:Lp(Ω)→W-1,p(Ω)is continuous,we have?fkl→?f=0 inW-1,p(Ω).This implies that f=const.so[f]=0.Thus

This is a contradiction.
(c)is equivalent to(d).We note that the operatorgrad=?:Lp(Ω)/R→W-1.p(Ω)is the dual operator of-div:and satisfies

for all[f]∈Lp(Ω)/R andφ∈(Ω).Therefore,if we apply the Banach closed range theorem,Im?is a closed subspace ofW-1,p(Ω)if and only if

This means that(c)and(d)are equivalent.
(d)implies(e).Assume that(d)and(c)hold.Sincegrad(Lp(Ω)/R)is a closed subspace ofW-1,p(Ω)from(c),it follows from the Banach closed range theorem that we have Imdiv=(Ker?)⊥.Since Ker?=R,we have Imdiv=,so we can see that

is a continuous and bijective linear operator.Therefore,from the Banach open mapping theorem,the inverse operator is continuous.Hence,for any f∈Lp′0(Ω),there exists a unique/Kerdiv such that divuf=f in,and there exists a constant C(p,Ω)such that

(e)implies(f).Assume thatΩis starlike with respect to an open ball of radius r>0 and the center x of which will be assumed without loss of generality to be at the origin.Define

We show that for anyφ∈˙D(Ω),there existvn=vn(φ)∈D(Ω)and a constant c2(p′,Ω)>0 independent ofφsuch that

and divvn→φin D(Ω)as n→∞.
In fact,from(e),for anyφ∈˙D(Ω),there exists[v]∈(Ω)/Kerdiv such that

and div[v]=φinΩ.By elementary calculation,we can see that

is achieved.Therefore,there existsu∈(Ω)such that

and divu=φinΩ.Letw=w(φ)be the extension ofuby 0 in RdΩ.Thenw∈W1,p′(Rd),

and divw=φinΩand divw=0 in RdΩ.Let n0≥1 be the smallest integer such that n0>2/r,and putλn=1-2/nr for all n≥n0andΩn={λnx;x∈Ω}(?Ω).We note that 0<λn<1.SinceΩis starlike with respect to B(0,r),the Thales theorem implies that for all n≥n0,dist(x,Γ)>2/n for all n≥n0and for all x∈Ωn.If we defineun(x)=λnw(x/λn)∈W1,p′(Rd),we see thatun=0 in RdΩn,divun=φ(·/λn)in Rd,whereφ(·/λn)designates the function defined byφ(x/λn)if x∈Ωnand by 0 if x∈RdΩn.Choose a mollifierρ∈C∞(Rd)such thatρ≥0,ρ(x)=0 for|x|≥1 andRdρ(x)dx=1,and defineρn(x)=ndρ(nx).Since for n≥n0,dist(x,Γ)>2/n for x∈Ωnand suppρn?,we can see thatwn=un*ρn∈C∞(Rd),that is,for x∈Rdand suppwn?For n≥n0,if we definevn=thenvn∈D(Ω)and satisfies


for all n≥n0.
We show that divvn→φin D(Ω)as n→∞.Sinceφ∈D(Ω),there existsα>0 such that dist(x,Γ)≥αfor all x∈suppφ.Since suppρn?there exist n1≥n0andβ>0 such that dist(x,Γ)≥βfor all x∈supp(φ(·/λn)*ρn)∪suppφfor n≥n1.Therefore,we have
supp(divvn)∪suppφ?K:=for all n≥n1.We have

Therefore,we have
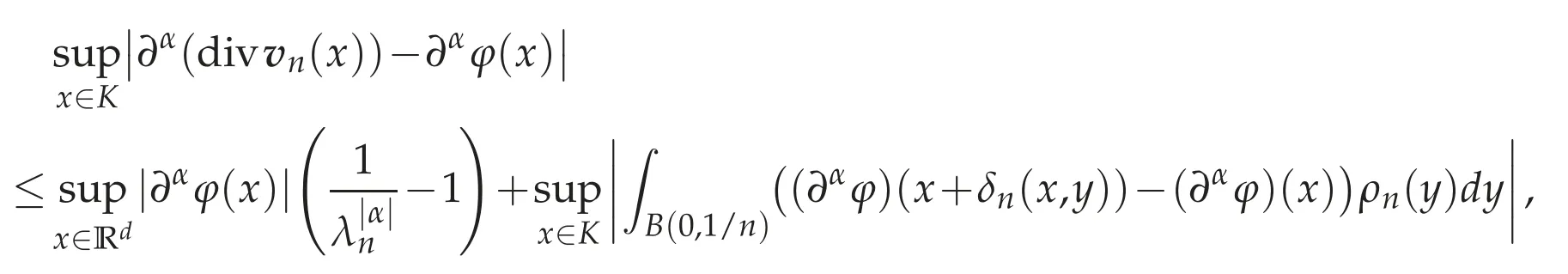
where
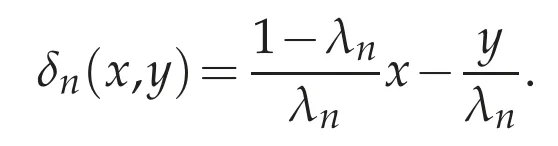
Here

Since?αφis uniformly continuous,we have

This implies that divvn→φin D(Ω)as n→∞.
(f)implies(g).
Step 1.The case whereΩis starlike with respect to an open ball.
Let f∈D′(Ω)and ? f∈W-1.p(Ω).It suffices to prove that
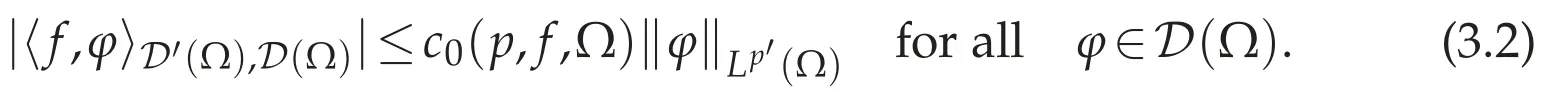
In fact,assume that(3.2)holds.Since D(Ω)is dense in Lp′(Ω),for anyφ∈Lp′(Ω),there existφn∈D(Ω)such thatφn→φin Lp′(Ω).From(3.2),we have

Therefore,{〈f,φn〉D′(Ω),D(Ω)}is a Cauchy sequence in R.We define

Clearly,the definition is independent of the choice of{φn}such thatφn→φin(Ω).Since
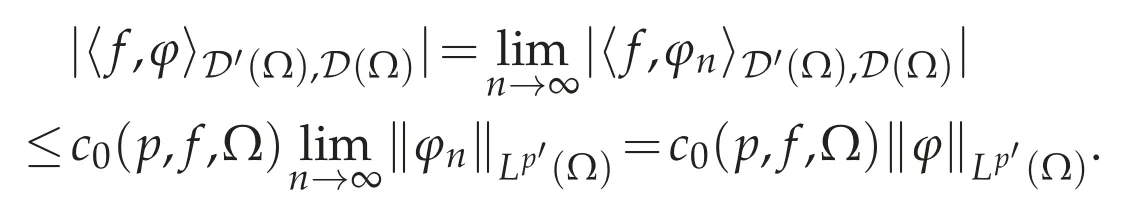
Thus f∈Lp(Ω).
We show(3.2).Letφ1∈D(Ω)such that=1.For anyφ∈D(Ω),define φ0=φ0(φ)by
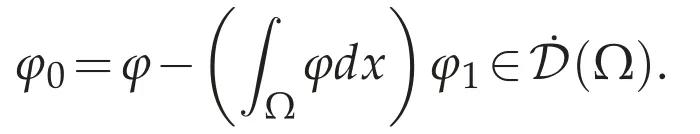

for allv∈D(Ω).From(f),there existvn=vn(φ0)∈D(Ω)such that
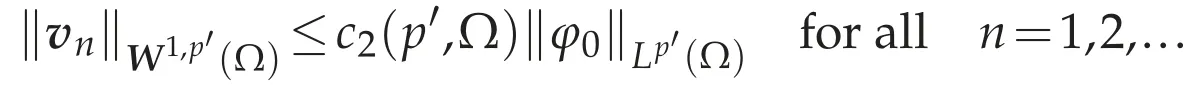
and divvn→φ0in D(Ω)as n→∞.Since
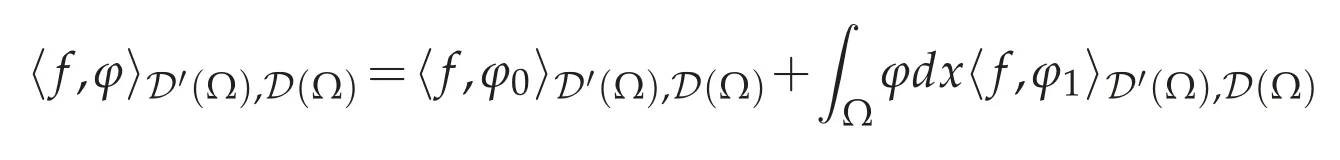
and

we have
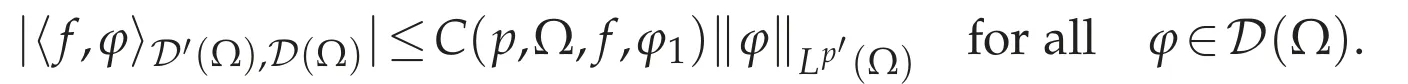
Thus(3.2)holds,and so(g)holds for the case where Ω is starlike with respect to an open ball.
Step 2.The case where Ω is a general bounded domain with a Lipschitz continuous boundary.
Let Ω be a bounded domain with a Lipschitz continuous boundary Γ.From Theorem 2.1,there exists a finite number of domains{Ωi}(i=1,2,...,N)such that eachΩiis contained inΩand starlike with respect to an open ball,and Ω=Ωi.Let f∈D′(Ω)and ? f∈W-1,p(Ω).Then there exists a constant C(f,p,Ω)>0 such that
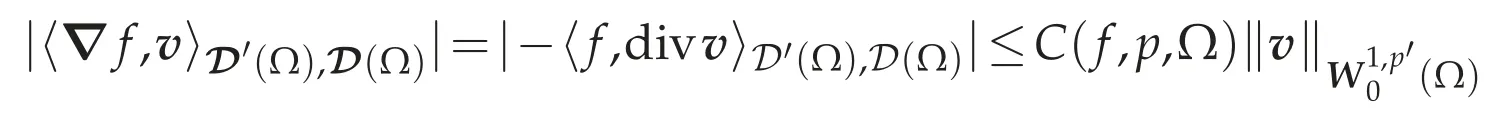
for allv∈D(Ω).For functionsθ∈D(Ωi)and θ∈D(Ωi),we write their extensions toΩby 0 and 0 inΩΩiby∈D(Ω)and∈D(Ω),respectively.For every i=1,...,N,if we define a linear form fi:D(Ωi)→R by
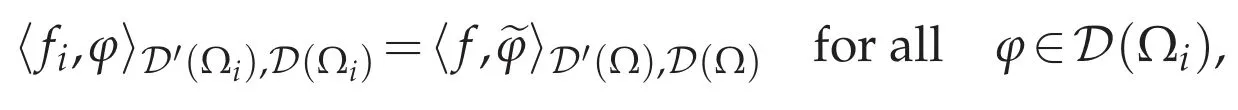
then for any φ∈D(Ωi),we have

Hence
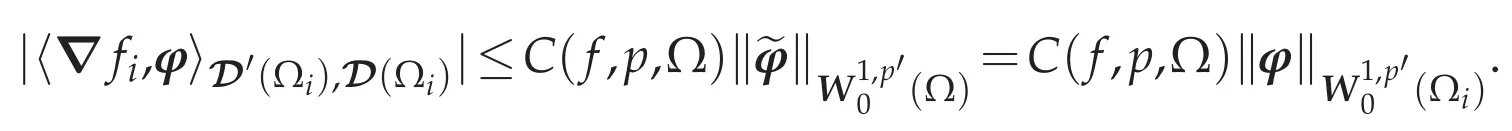
Since D(Ωi)is dense in(Ωi),we have ? fi∈W-1,p(Ωi).By Step 1,we see that fi∈Lp(Ωi),so
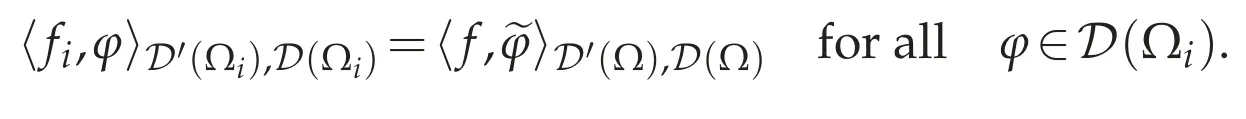
Let Ωi∩ Ωj/=?.Then for anyφ∈D(Ωi∩ Ωj),if we write the extension ofφby 0 on Ω(Ωi∩ Ωj)by,then

for allφ∈D(Ωi∩Ωj).Since fi∈D′(Ωi)?D′(Ωi∩Ωj),we have
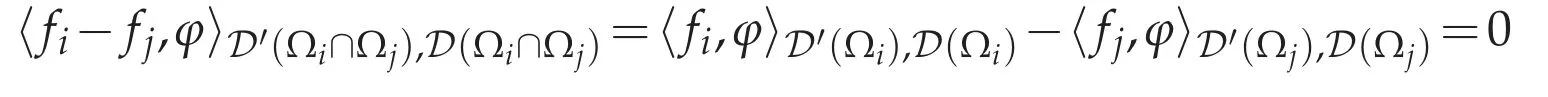
for allφ∈D(Ωi∩Ωj).Thus we have fi=fjin D′(Ωi∩Ωj).Therefore we can define a function=fiinΩi(i=1,...,N).Then we have.Letφ∈D(Ω),and letbe a partition of unity associated withof the compact set suppφ,i.e.,αi∈D(Ω),suppαi?Ωiand=1 in a neighborhood of supp φ.Then we have

(g)implies(a).Clear.
This completes the proof of Theorem 3.1.
Remark 3.2.Since we can prove that the classical J.L.Lions lemma(a)holds(cf.Ciarlet[11,p.381 and the footnote]),or the Ne?as inequality(b)(cf.[19,Theorem 1]or[10,Remark IV.1.1])directly,consequently if Ω is a bounded domain with a Lipschitz-continuous boundary,then all of(a),...,(g)are true.
4 An application to the existence of a weak solution to the Maxwell-Stokes type problem
In this section,let Ω be a bounded domain in R3with a C1,1boundaryΓ,and 1<p<∞.We will apply Theorem 3.1.
Since we allowΩto be a multiply-connected domain with holes,we assume thatΩsatisfies the following conditions as in Amrouche and Seloula[4](cf.Amrouche and Seloula[3],Dautray and Lions[12]and Girault and Raviart[15]).Ω is locally situated on one side ofΓand satisfies the following(O1)and(O2).
(O1)Γ has a finite number of connected componentsΓ0,Γ1,...,ΓIwith Γ0denoting the boundary of the infinite connected component of R3.
(O2)There exist J connected open surfaces Σj,(j=1,...,J),called cuts,contained inΩsuch that
(a)each surfaceΣjis an open subset of a smooth manifold Mj,
(b)?Σj?Γ(j=1,...,J),where?Σjdenotes the boundary ofΣj,andΣjis non-tangential toΓ,
The number J is called the first Betti number and I the second Betti number.We say thatΩis simply connected if J=0 andΩhas no holes if I=0.If we define
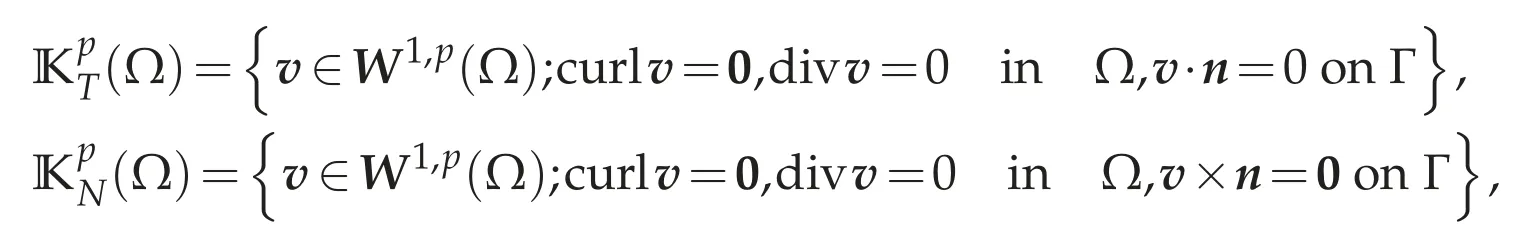
then it is well known that dim=J and dim=I.In the latter,we need a basis ofas follows.(1≤i≤I)be a unique solution of the problem


dσis the surface area ofΓ.Then we can see thatis a basis of(cf.[4,Corollary 4.2]).
We introduce some spaces of vector functions.Define a space

equipped with the norm

We note that Xp(Ω)is a Banach space with respect to the given norm as above.Moreover,we note that ifv∈Lp(Ω)and curlv∈Lp(Ω),then the tangent tracen×v∈W-1/p,p(Γ)is well defined and

for anyφ∈W1,p′(Ω),and that ifv∈Lp(Ω)and divv∈Lp(Ω),then the normal tracev·n∈W-1/p,p(Γ)is well defined and
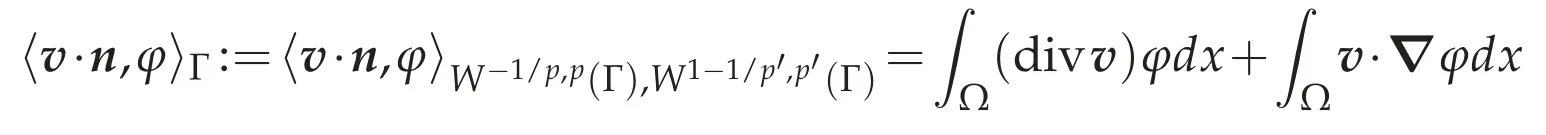
for anyφ∈W1,p′(Ω)(cf.[4,p.45]).
Furthermore,define a closed subspace of Xp(Ω)by

From[4,(1.5)],we see that,where the symbolmeans that the inclusion mapping is continuous,and thus there exists a constant C>0 depending only on p andΩsuch that

Forv∈Lp(Ω),divv∈W-1,p(Ω)and curlv(?W-1,p(Ω))are defined by

and
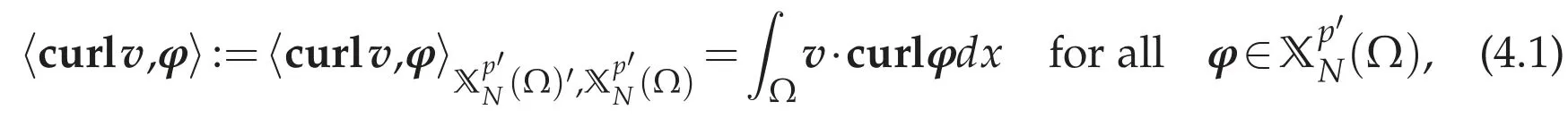
respectively.In fact,it follows from the H¨older inequality that
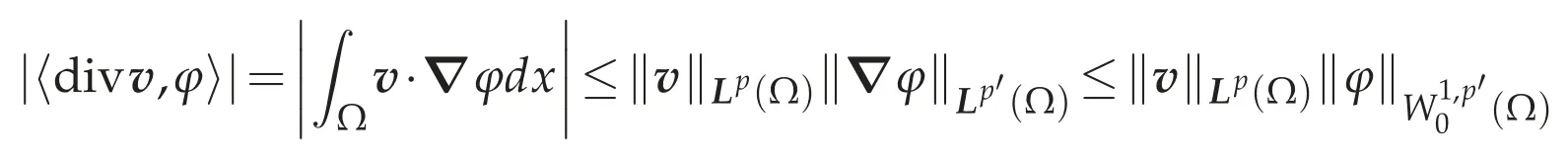

holds.Similarly,we see that


holds.Thus the linear operators div:v∈Lp(Ω)→divv∈W-1,p(Ω)andcurl:v∈Lp(Ω)→curlvare continuous.
For brevity,we write the closed subspaces(Ω,div0)ofW1,p(Ω)by

The following inequalities are used frequently(cf.[4]).If we define

then we can see that X1,p(Ω)W1,p(Ω)and there exists a constant C>0 depending only on p and Ω such that

Moreover,we can deduce the following(cf.[4,p.40]):for anyv∈W1,p(Ω)withv×n=0 onΓ,we have

Thus we have the following.
Lemma 4.1.(Ω)is a reflexive,separable Banach space with the norm
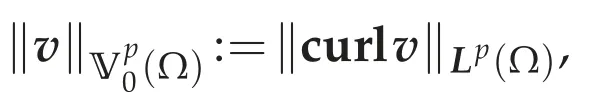
which is equivalent to theW1,p(Ω)-norm.
Assume that S(x,t)is a Carath′eodoty function inΩ×[0,∞)satisfying the following structural conditions.
For a.e.x∈Ω,S(x,t)∈C2((0,∞))∩C([0,∞))as a function of t,and there exist 1<p<∞and constants 0<λ≤Λ<∞such that for a.e.x∈Ωand t>0,
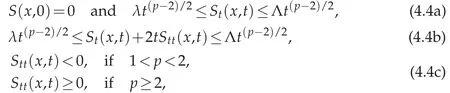
where St=?S/?t,Stt=?2S/?t2.We note that(4.4a)implies that
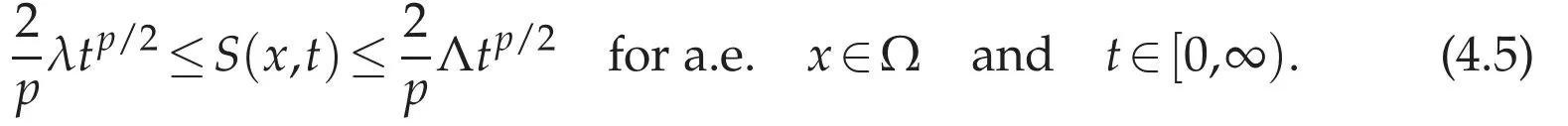
Example 4.1.Assume that S(x,t)=ν(x)g(t)tp/2,whereνis a measurable function inΩsatisfying

for some constantsν*andν*.If a function g(t)≡1,it follows from elementary calculations that(4.4a)-(4.4c)hold.This case corresponds to the p-curlcurl operator(cf.Aramaki[7]).
As an another example,we can take

Then we can see that S(x,t)=ν(x)g(t)tp/2also satisfies(4.4a)-(4.4c)if p≥2(cf.Aramaki[8,Appendix B]).
Lemma 4.2.If S(x,t)satisfies(4.4a)and(4.4b),then for a.e.x∈Ω,J[a]=S(x,|a|2)is strictly convex.
For the proof,see[8,Lemma 2.3].
We also use the following lemma with respect to the monotonicity of St.
Lemma 4.3.There exists a constant c>0 such that for alla,b∈R3,
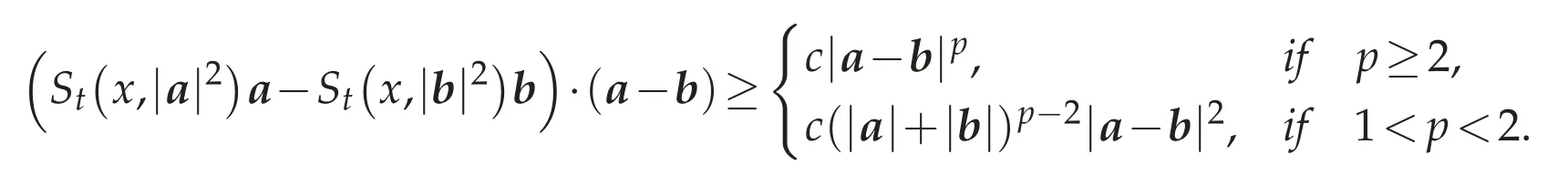
In particular,Stis strictly monotone,that is,

For the proof,see[7,Lemma 3.6].
Now we consider a stationary Maxwell-Stokes type problem.To do so,let S(x,t)be a Carath′eodory function inΩ×[0,∞)satisfying(4.4a)-(4.4c),and let(Ω)′be given.We consider the following Maxwell-Stokes type problem:to find(u,π)∈W1,p(Ω)×(Ω)such that
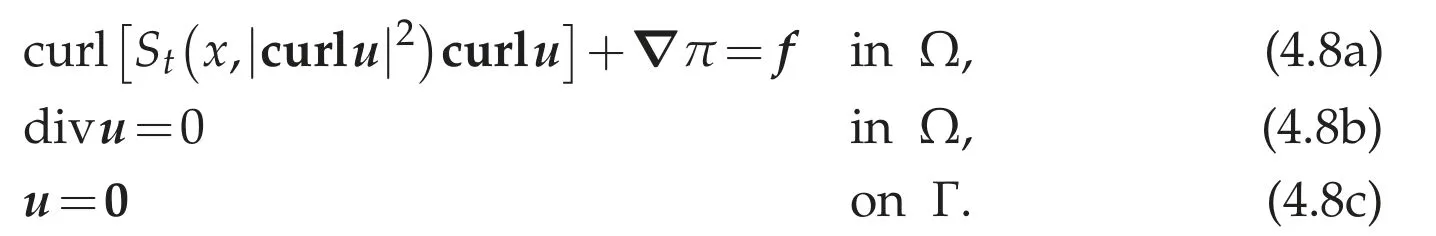
For givenfwe give the notion of weak solutions for(4.8a)-(4.8c).
Definition 4.1.We say that(u,π)∈W1,p(Ω)×(Ω)is a weak solution of(4.8a)-and(u,π)satisfies
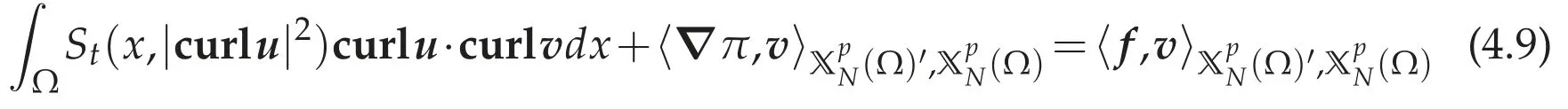
for all.
We have the following theorem.
Theorem 4.1.Assume that 1<p<∞andf∈(Ω)′.Then the problem(4.8a)-(4.8c)has a unique weak solution(u,π)∈W1,p(Ω)×Lp′0(Ω),and there exists a constant C>0 depending only on p,λ,ΛandΩsuch that

Proof.For givenf∈(Ω)′,we consider the following minimization problem:to findu∈(Ω)such thatuis a minimizer of

where

Here we say thatu∈(Ω)is a minimizer of(4.11),if R[u]=R*.We show that(4.11)has a unique minimizeru∈,and that there exists a constant C>0 dependent only on p,λandΩsuch that
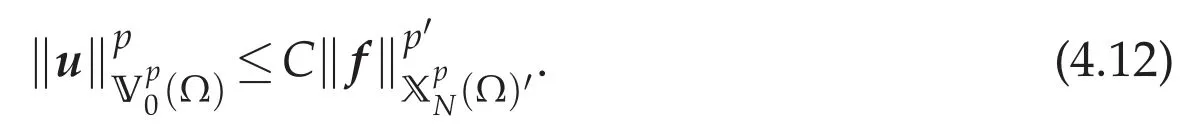
Ifu,v∈andu/=v,then we havecurlu/=curlv.Because,if curlu=curlvinΩ,then we have curl(u-v)=0,div(u-v)=0 inΩand〈(u-v)·n,1〉Γi=0 for i=1,...,I.Thus we haveu=vfrom(4.3).This contradict the hypothesis.Thus,it follows from Lemma 4.2 that R is a strictly convex and clearly proper functional.From Aramaki[7],we can see that R is lower semi-continuous on.By(4.5)and the H¨older and Young inequalities,we have

for anyε>0.If we chooseε>0 so thatε=λ/(2p),we can see that R is coercive onHence it follows from Ekeland and Temam[13,Proposition 1.2]that the minimization problem has a unique minimizeru.
By the Euler-Lagrange equation

we can see thatusatisfies

for allv∈If we takev=uas a test function of(4.13),it follows from(4.4a),the H¨older and Young inequalities that for anyε>0,there exists a constant C(ε)>0 such that
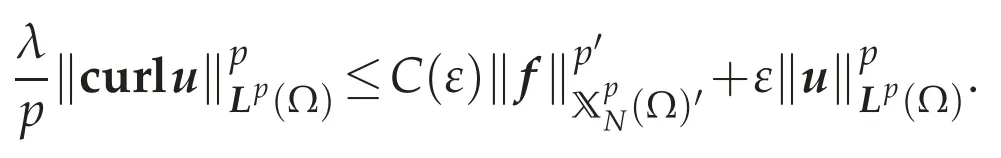
If we choose a small enoughε>0,then there exists a positive constant C depending only on p,λandΩsuch that(4.12)holds.Since

from(4.4a),we see that St(x,|curlu|2)curlu∈Lp′(Ω).By(4.1),we can rewrite(4.13)into the form

for allv∈(Ω).Here we note that the Ne?as inequality(b)in Theorem 3.1 holds(cf.[19]or[14]).SinceΩis a C1,1domain,it follows from(4.14)that we can see that the coarse version of the de Rham theorem(d)in Theorem 3.1 holds.Thus there exists[π]∈Lp′(Ω)/R such that

Since Lp′(Ω)/R is isomorphic to(Ω),we may assume thatπ∈(Ω).Furthermore,since St(x,|curlu|2)curlu∈Lp′(Ω),we have curl[St(x,|curlu|2)curlu]∈Sincewe see thatand
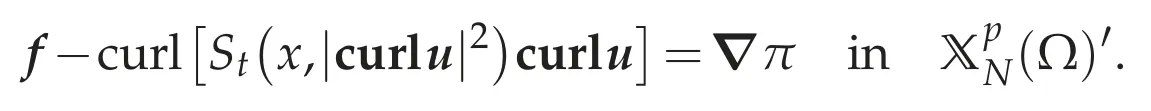
Thus(4.9)holds,that is,(u,π)is a weak solution of(4.8a)-(4.8c).
Next,we show the estimate(4.10).We takev=u∈(Ω)as a test function of(4.9).Since forv=u∈(Ω)we have

the inequality(4.12)holds.
We claim that the following Poincar′e type inequality holds.
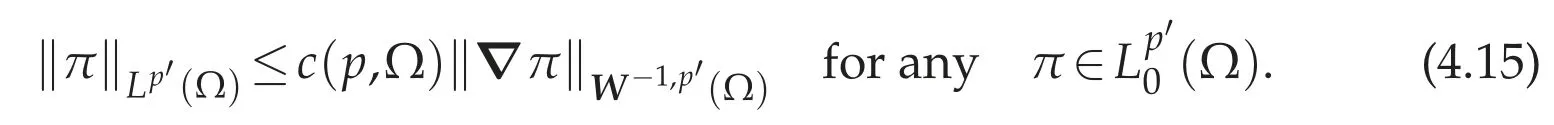
Indeed,by Theorem 3.1(e),for anyφ∈(Ω),there existsv∈(Ω)such that divv=φin(Ω)and there exists a constant c(p,Ω)such that

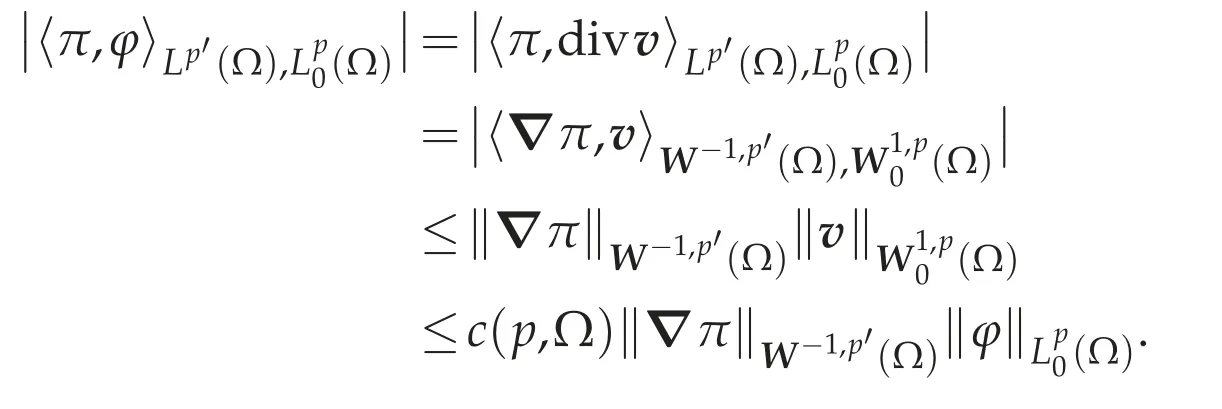
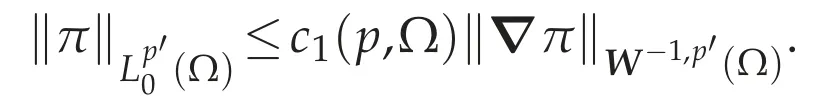
Therefore,we get the estimate(4.15).Since?π=f-curl[St(x,|curlu|2)curlu]∈using(4.12),we have
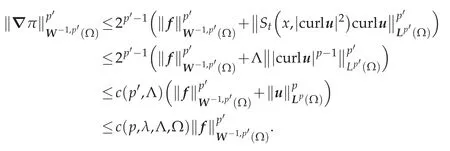
Since,we have(Ω),so

Thus taking(4.12)and(4.15)into consideration,we obtain the estimate(4.10).
Finally,we show the uniqueness of a weak solution for(4.8a)-(4.8c).Let(u1,π1)and(u2,π2)be two weak solutions of(4.8a)-(4.8c).Takingv=u1-u2∈Vp0(Ω)as a test function of(4.9),we have

Therefore,we can see that
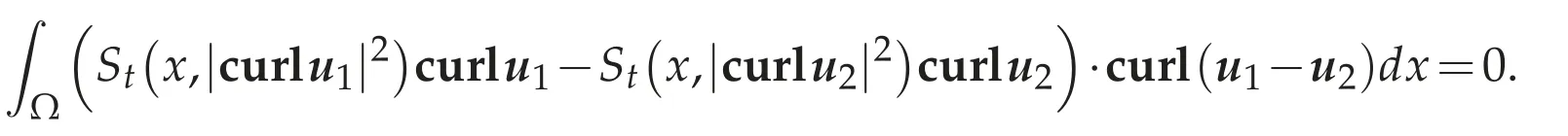
Hence,by the strict monotonicity of St(Lemma 4.3),we haveu1=u2.Furthermore,if we choosev∈D(Ω)as a test function of(4.9),we have
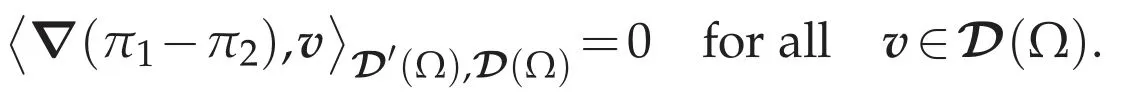
Since?(π1-π2)=0 in D′(Ω),we can see thatπ1-π2is equal to a constant.Since πi∈(Ω),we see that the constant is equal to zero,so we haveπ1=π2inΩ.
Remark 4.1.In our previous paper[8],we showed that the following system

has a unique weak solution under the hypothesis
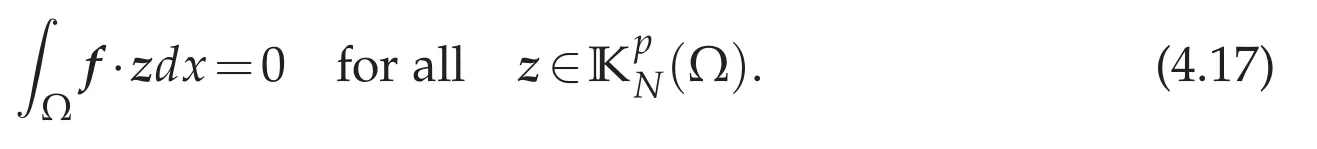
However,in Theorem 4.1,the hypothesis(4.17)is unnecessary for the existence theory of a weak solution for(4.8a)-(4.8c).Thus our result is new.
Next we consider the following inhomogeneous Maxwell-Stokes type problem.
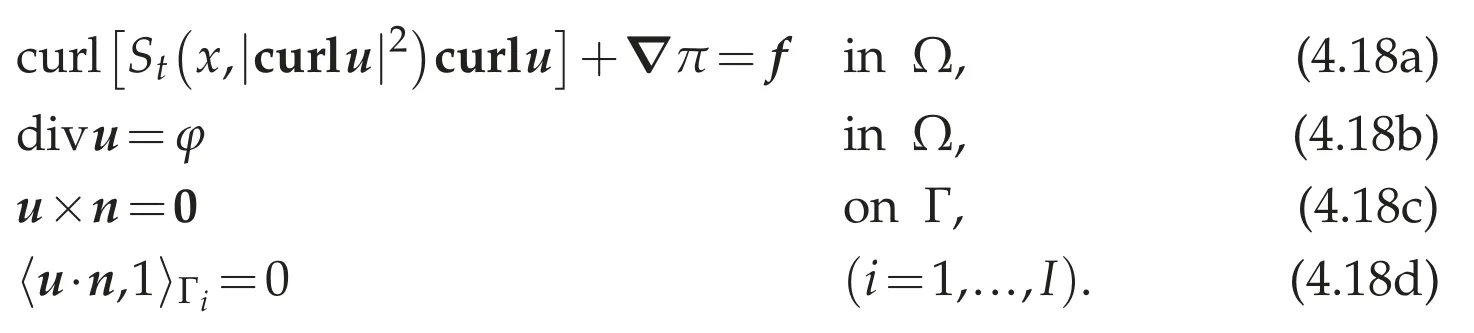
Corollary 4.1.Assume that 1<p<∞,f∈(Ω)′andφ∈Lp(Ω).Then the problem(4.18a)-(4.18d)has a weak solution(u,π)∈W1,p(Ω)×(Ω).In particular case where Ωhas no hole,there exists a constant C>0 depending only on p,λ,ΛandΩsuch that


Proof.Let(w,π)be a unique weak solution of(4.8a)-(4.8c).We consider the following div-curl problem:From Aramaki[5,Theorem 3.5],the problem(4.19)has a solutionu0∈W1,p(Ω).In particular,ifΩhas no hole,there exists a constant C1>0 depending only on p andΩsuch that

If we define
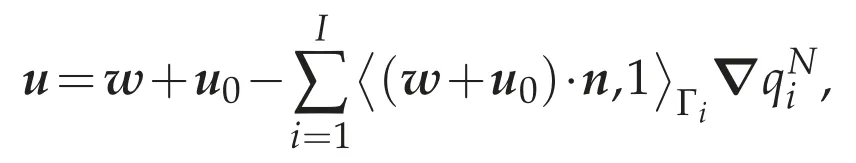

Thususatisfies(4.18b)-(4.18d).Sincecurlu=curlwinΩand(u,π)satisfies(4.9),we can see that(u,π)is a weak solution of(4.18a)-(4.18d).In particular case whereΩhas no holes,from(4.10)and(4.20),we have

This completes the proof.
5 An application of J.L.Lions lemma to the Korn inequality
In this section,we consider the Korn inequality which plays a crucial role in linearized elasticity.
We have the following Korn inequality inW1,p(Ω).
Theorem 5.1.LetΩbe a domain of Rdand 1<p<∞.Then the J.L.Lions lemma(Theorem 3.1(a))implies the following Korn inequality inW1,p(Ω):there exists a constant C=C(p,Ω)>0 such that

wheree(v)=(eij(v))1≤i,j≤dwith
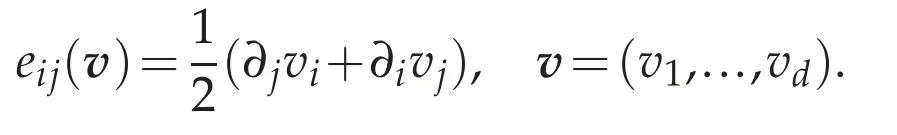
Proof.Step 1.Define
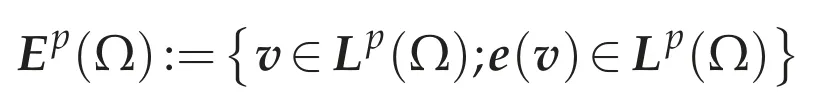
equipped with the norm

Then clearlyEp(Ω)is a Banach space.We claim thatEp(Ω)=W1,p(Ω).Indeed,clearlyW1,p(Ω)?Ep(Ω).Letv∈Ep(Ω).Then for every i,k=1,...,d,?kvi∈W-1,p(Ω).Since

it follows from J.L.Lions lemma(Theorem 3.1(a))that?kvi∈Lp(Ω)for k=1,...,d.Therefore,vi∈W1,p(Ω),sov∈W1,p(Ω).
Step 2.Korn’s inequality.
The canonical injection i:W1,p(Ω)→Ep(Ω)is injective and continuous.By Step 1,the injection i is surjective.Therefore,from the Banach open mapping theorem,i-1is also continuous.This implies that there exists a constant C=C(p,Ω)>0 such that

This implies(5.1).
Acknowledgements
The author would like to thank the anonymous referee(s)for useful comments and suggestions.
Appendices
In this and next appendices,we discuss on relations to the J.L.Lions lemma to other fundamental results.
A Relation between the J.L.Lions lemma and a simplified version of the de Rham theorem
We have the following theorem.
Theorem A.1.LetΩbe a domain of Rd.Then the J.L.Lions lemma(Theorem 3.1(a))implies that the following simplified version of the de Rham theorem:For anyh∈W-1,p(Ω)satisfying

Conversely,the simplified version of the de Rham theorem implies the J.L.Lions lemma(Theorem 3.1(a)).Proof.Leth∈W-1,p(Ω)satisfy

From Theorem 2.2,choose bounded domainsΩj?Ω(j=1,2,...)such that?Ωjis of classandFor anyvj∈(Ωj)satisfying divvj=0 inΩj,defineas an extension ofvjby 0 on RdΩj.Let{ρn}be the mollifier as in the proof of Theorem 3.1.Then there exists n0(j)and a compact set Kj?Ω such that supp(divvj)*ρn=0 in Rdfor any n≥n0(j)andfor any n≥n0(j),div(vj*ρn)=For j≥1,lethj∈W-1,p(Ωj),wherehjis the restriction ofhtoΩj,i.e.,

identified with a subspace of(Ω).Then we have
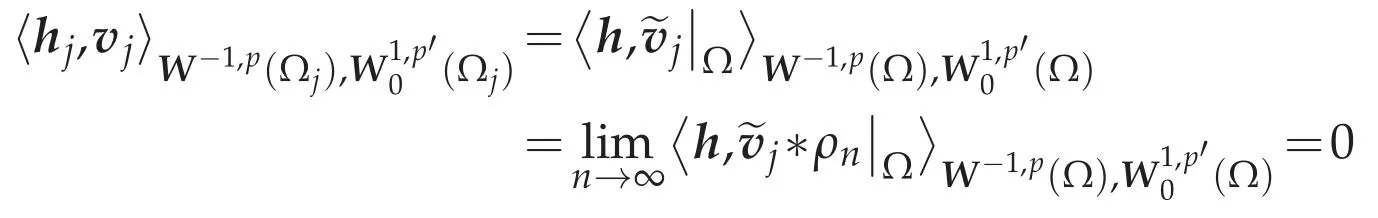
for allvj∈(Ωj)satisfying divvj=0 inΩj.By Theorem 3.1(d),there exists qj∈(Ωj)such thathj=?qjinW-1,p(Ωj).For j≥1,let

Thenπj∈Lp(Ωj)andhj=?πjinW-1.p(Ωj).Ifhj=?πjinW-1.p(Ωj)andhj+1=?πj+1inW-1.p(Ωj+1),then=const..Since Ω1?Ωjandπjdx=0,the constant is equal to zero.Henceπj=πj+1a.e.in Ωj.For any x∈Ω,there exists j(x)≥1 such that x∈Ωjfor j≥j(x).Hence if we define=πj(x)for j≥j(x),then(Ω)?D′(Ω).For anyφ∈D(Ω),there exists an integer j(φ)≥1 such that suppφ?Ωjfor j≥j(φ).Hence we have

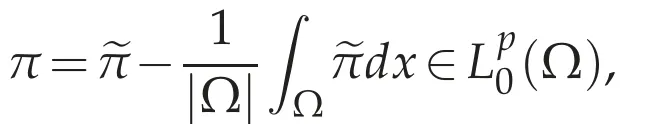
then we haveh=?πinW-1,p(Ω).
Conversely,if the simplified version of the de Rham theorem holds,then(d)in Theorem 3.1 holds,so the J.L.Lions lemma in Theorem 3.1(a)holds.
Remark A.1.Theorem A.1 means that the coarse version of the de Rham theorem in Theorem 3.1 and simplified version of the de Rham theorem in Theorem A.1 are equivalent.
B Relation between the J.L.Lions lemma and a weak version of Poincar′e lemma
In this section,we assume thatΩis simply connected bounded domain of Rdwith a C1,1-boundary.
Theorem B.1.LetΩbe a simply connected domain with a C1,1-boundary.Then the J.L.Lions lemma(Theorem 3.1(g))implies the following weak Poincar′e lemma:ifh∈W-1,p(Ω)satisfiescurlh=0 inW-2.p(Ω),then there exists aπ∈Lp(Ω),unique up to an additive constant such thath=?πinW-1,p(Ω).
Proof.Assume that the J.L.Lions lemma(Theorem 3.1(g))holds andh∈W-1,p(Ω)satisfiescurlh=0 inW-2,p(Ω).SinceΩis bounded domain of Rdwith a C1,1-boundary,it follows from[2,Theorem 4.18]that the following Stokes problem
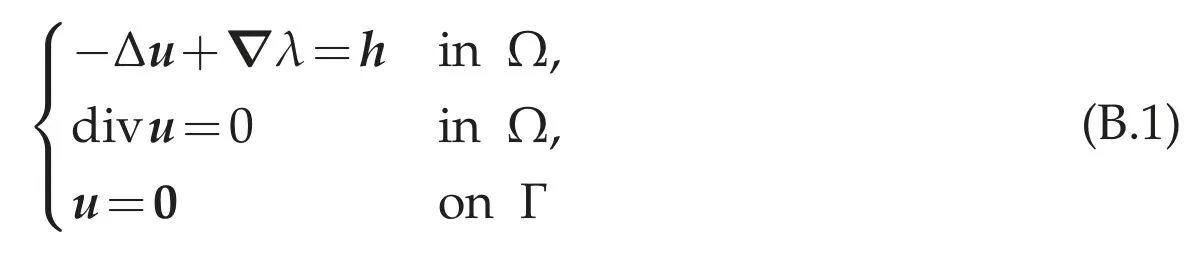
has a unique solution(u,[λ])∈(Ω)×Lp(Ω)/R,and there exists a constant C>0 depending only on p andΩsuch that
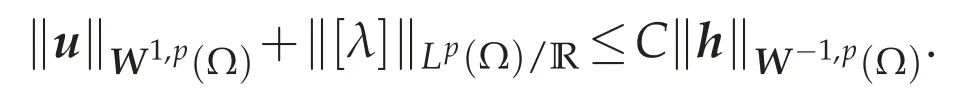
Since curlh=0 inW-2,p(Ω),we have
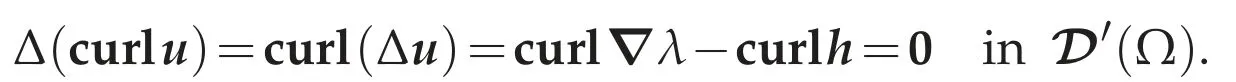
Sincecurlu∈Lp(Ω)?(Ω),we have curlu∈C∞(Ω)according to the hypoellipticity of the Laplacian(cf.Ciarlet[11,Theorem 6.4-2]).SinceΔu=-curlcurlu+?divu=-curlcurlu∈C∞(Ω),we see thatΔu∈C∞(Ω)and curl(Δu)=0 inΩ.By the classical Poincar′e lemma,there exists∈C∞(Ω)such that?=Δu=?λ-hinW-1,p(Ω).Defineπ=λ-∈D′(Ω),we have?π=?λ-?=h∈W-1,p(Ω).Then(g)in Theorem 3.1 implies thatπ∈Lp(Ω).
Remark B.1.In the particular case p=2,it is known that Theorem B.1 holds under the hypothesis thatΩis only simply connected domain with a Lipschitz continuous boundary,and moreover the converse also holds,that is,the weak Poincar′e lemma on any simply connected domain of Rdimplies that the J.L.Lions lemma holds on any domain with a Lipschitz continuous boundary.This comes from that we can solve the equation(B.1)under the assumption thatΩis a simply connected domain with a Lipschitz continuous boundary.See[1,Theorem 5.1]and references therein.
 Communications in Mathematical Research2021年2期
Communications in Mathematical Research2021年2期
- Communications in Mathematical Research的其它文章
- Weighted and Maximally Hypoelliptic Estimates for the Fokker-Planck Operator with Electromagnetic Fields
- The Reflexive Selfadjoint Solutions to Some Operator Equations
- A Level Set Representation Method for N-Dimensional Convex Shape and Applications
- Spectral Properties of an Energy-Dependent Hamiltonian
